Rep:Mod:MyPro
Molecule Analysis: Borane
The Method and Basis Set Used
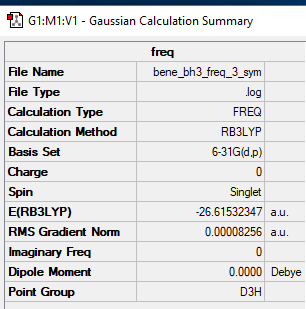
The calculation method used to study the optimised form of a BH3 molecule was an RB3LYP, along with a basis set of 6-31G(d.p). The full 'Summary' and 'Item' tables are shown below.
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-1.537772D-14
Optimization completed.
-- Stationary point found.
Full mass-weighted force constant matrix: Low frequencies --- -0.7746 -0.4957 -0.0054 9.9818 14.3012 14.3222 Low frequencies --- 1163.0178 1213.1971 1213.1998
An optimised borane molecule |
Vibrational Spectrum for BH3
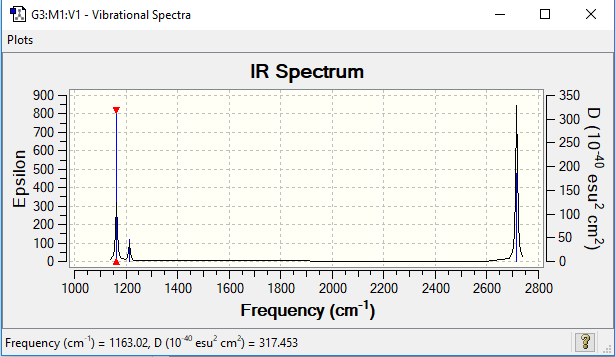
The vibrational data is plotted below.
| wavenumber (cm-1) | intensity (arbitrary units) | symmetry | IR active? | type |
| 1163 | 92 | A2" | yes | out-of-plane bend |
| 1213 | 14 | E' | very slight | bend |
| 1213 | 14 | E' | very slight | bend |
| 2582 | 0 | A1' | no | symmetric stretch |
| 2715 | 126 | E' | yes | asymmetric stretch |
| 2715 | 126 | E' | yes | asymmetric stretch |
A change in dipole moment must occur for a vibration to be IR active. As a result, the symmetric stretch of the a1' orbital does not appear on IR plots as no change in dipole is observed. Degeneracy of the e' orbitals further reduces the number of peaks seen in the IR plot to three.
An Analysis of the IR Spectrum of Borane
Having confirmed the optimisation of the borane molecule from a frequnecy analysis, the MOs were studied after drawing an MO diagram using ChemDraw; MO1 is a core orbital and is deep in energy (-6.77140au). The other MOs are valence orbitals, as seen from the jump in energy between MO1 and MO2. The unoccupied orbitals are more diffuse than the occupied orbitals and are higher in energy, in accord of the Aufbau principle. Another aspect studied in the MO diagrams can be seen from the larger contribution to the bonding orbitals from the more electronegative H fragments, and the larger contribution to the antibonding orbitals from the more electropositive B fragments. A non-bonding orbital is also observed due to the absence of an a2" symmetry orbital. The antibonding orbitals are destabilised more than the bonding orbitals.
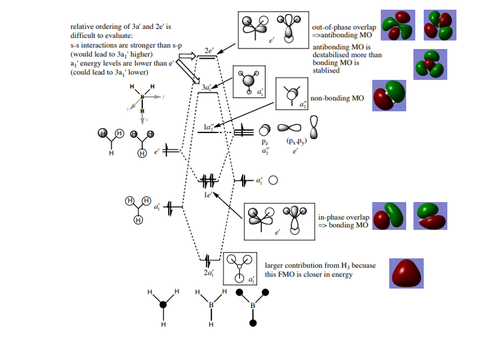
A molecule of borane has seven valence AOs and so seven MOs are formed. There are six electrons involved, and so only the first three valence orbitals are occupied. The real MOs obtained from analysis of the compound in Gaussview is placed next to the predicted MOs using LCAO, and in comparison to these real MO diagrams, it can be confirmed that the LCAO used when drawing the MO diagram with hand is an accurate and reliable method for the analysis of MOs. On the other hand, all real MOs overlap and mix very slightly, of which is neglected in LCAO.
Nice additional description of the MOs of BH3 highlighting the different contributions from the fragments. Smf115 (talk) 22:11, 13 May 2019 (BST)
An Analysis of Ammonia-Borane
Having optimised the structures of ammonia and ammonia borane using GaussView, the following energy values were obtained: E(BH3)=-26.61532363 Hartree E(NH3)=-56.55776873 Hartree E(H3B-NH3)=-83.22469032 Hartree
ΔE=E(NH3BH3)-[E(NH3)+E(BH3)] =(-83.22469032)-(-26.61532363)-(-56.55776873) =-0.05159796 Hartree =-135 kJ/mol =135 kJ/mol
In comparison to published results, the value obtained reflects the weaker bond assumed by the Gaussview program. Literature values put the B-N bond strength at 377.9 ± 8.7 kJ/mol. The large numerical differences between the two values can be because Gaussview neglects MO mixing and electron cloud interactions when real moieties react together to form compounds.
Correct calculation and good consideration of the accuracy of the resulting association energy calculated. You have used a sensible comparison which is great, however, your literature value lacks a reference. The final comment is a good suggestion but not quite correct. You are also missing any sections on your NH3 and NH3BH3 molecules themselves! The optimisation/frequency information and the log files should have been present for both structures. Smf115 (talk) 22:12, 13 May 2019 (BST)
Molecule Analysis: Nitrogen Triiodide
The Method and Basis Set Used
The calculation method used to study the optimised form of a BH3 molecule was an RB3LYP. along with a basis set of 6-31G(d.p). The full 'Summary' and 'Item' tables are shown below.
Item Value Threshold Converged? Maximum Force 0.000140 0.000450 YES RMS Force 0.000092 0.000300 YES Maximum Displacement 0.001083 0.001800 YES RMS Displacement 0.000807 0.001200 YES
Full mass-weighted force constant matrix: Low frequencies --- -12.7235 -12.7174 -6.4219 -0.0039 0.0189 0.0620 Low frequencies --- 101.0768 101.0775 147.4583
An optimised Nitrogen Triiodide molecule |
The optimised bond length of the B-I bond in nitrogen triiodide was calculated as 2.18438Å.
Project Section
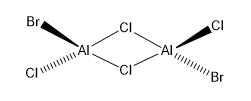
Al dimers are widely studied in Inorganic Chemistry. Usually, dimerisation occurs via Al-Halide-Al bonds with 2c-2e bonds formed using the electronegative electrons of the Cl and Br elements involved. The symmetry labels of the dimers vary according to the bridging halide atom along with the geometrical isomerisation of the four terminal halide atoms. The symmetry labels of the five isomers of Al2Cl4Br2 are shown below.
This is the lowest energy isomeric form of the dimer being considered, and is further studied below.
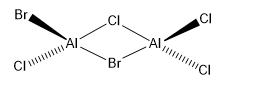
Another aspect studied was the difference in energy between the structures with Cl bridges and that between Br bridges. The isomer with trans terminal Br atoms and Cl bridges (isomer 3) had a C2H symmetry and an energy of (-7469.53758218)au, whereas the isomer with bridging Br ions (isomer 1) had a D2H symmetry and an energy of (-7469.54264935)au. The relative energy difference between these isomers can be calculated as:
ΔE=E(bridging Cl ions, trans Br ions)-E(bridging Br ions) =(-7469.53758218)-(-7469.54264935) =-0.00506717Hartree =-13.30 kJ/mol =13 kJ/mol
The calculation projects a reasonable conclusion of the relative stability of the dimers involved. It is known that the more negative the energy values seen the more stable the dimer formed, as it is deeper in energy and requires a larger input of heat for ionisation to occur; Br is less electronegative than Cl and ensures the formation of stronger bonds by , making the dimer with Br bridges the more stable isomer of the two being compared.
Furthermore, the dissociation energy for the lowest energy conformer of the dimer with bridging Br ions into 2AlCl2Br was also calculated, as seen below:
E(dissociation)=E(bridging Br ions)-2(tri-organo Al monomer)
=(-7469.53758218)-2(-3734.74850528)
=-0.04563879au
=119.82 kJ/mol
=120 kJ/mol
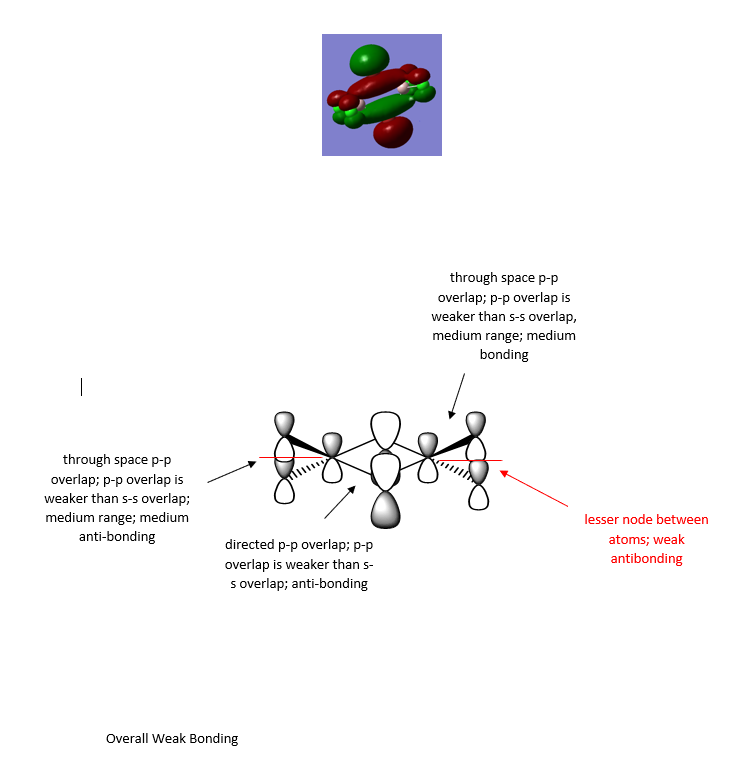
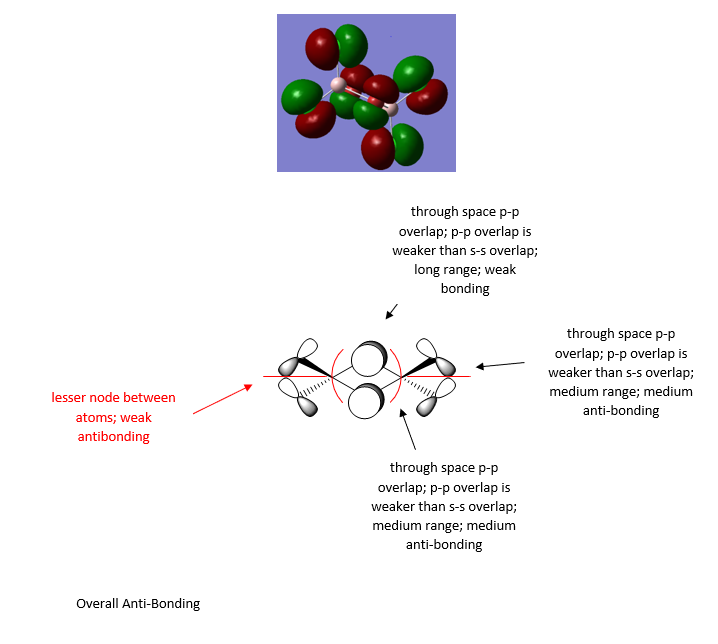
The MO diagrams of isomer 1 are further explored here through the selection of three MOs ranging from highly bonding to highly antibonding using Gaussview. The MOs below MO 17 can be considered as core orbitals and are ignored, as can be seen from the energy jump between MO 16 and MO 17, with values of -56.16824au at MO 16 and -9.46927au at MO 17. The significance of the energy of overlap of orbitals depends on the energy difference of orbitals, the extent of orbital overlap Sab and the orbital coupling Hab, whereby Sab relates to direct spatial overlap of orbitals, but Hab involves the orbital interactions modified by the local environment of the molecule.
Here are three MOs of isomer 1ː
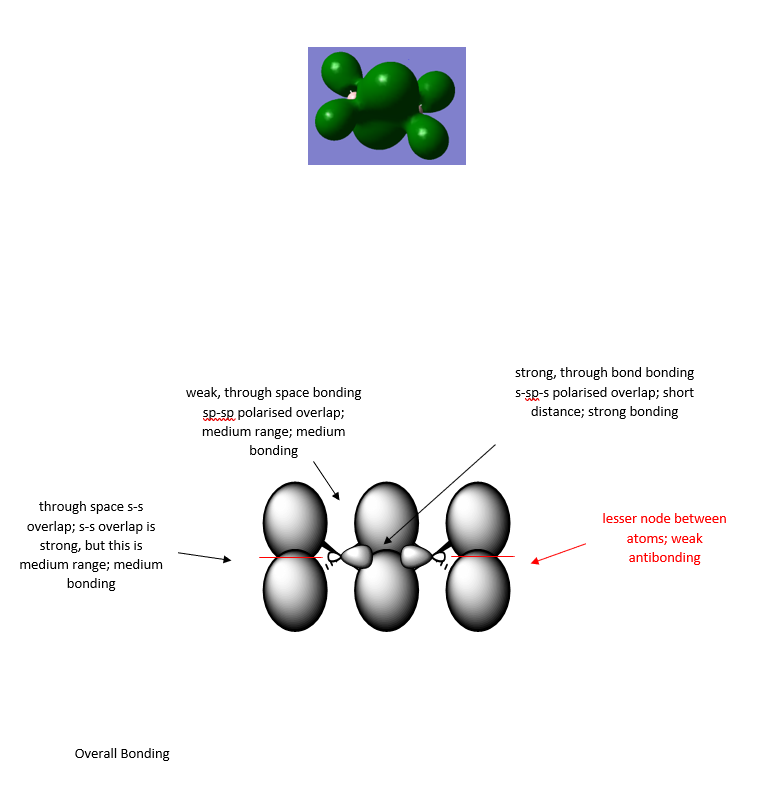
Overall a good attempt at analysing the MO and the key interactions. You’ve chosen a good range of MOs (but not labelled which ones!) and have evaluated the overall MO character well. However, some of the main interactions have been missed or not described correctly . The presentation of the LCAOs is ok but the overall section is poorly presented and some of the LCAOs are wrong. For example, the first MO looks more like it has no contribution (or a very weak opposite phase s-orbital) on the Al and there doesn’t appear to be a nodal plane between the terminal Cl/Br as there is not change in phase. Smf115 (talk) 22:11, 13 May 2019 (BST)
Overall an ok report. In both sections, where you have considered the questions it is good but they are let down by lacking the structure information and files required. Smf115 (talk) 22:11, 13 May 2019 (BST)