Rep:Mod:Mp3214

Monish Nakhwal Third Year Computational Lab Transition States and Reactivity

Introduction

Gaussian can be used to calculate optimizations and vibrational frequencies of reaction reactants, transition states and products. Gaussian achieves these calculations based on Born Oppenheimer approximation where the electronic distribution of a molecule move instantaneously to the movement of nuclei. Most calculations were done at the PM6 level to save time, however some (mostly for exercise 2) were done at the B3LYP/6-31G(d) level.

Figure 1. A reaction pathway showing the corresponding points on a PES on the right

A potential energy surface PES is a mathematical function that gives the energy of a molecule as a function of its geometry based on Born-Oppenheimer Approximation. As a polyatomic molecule often has 3N-6 geometric degrees of freedom, the PES is likely to possess 3N-6 dimensions but is usually reduced to 3-D representation.

Stationary points refer to places on the potential energy surface with a zero gradient vector (first derivative of the energy with respect to nuclear coordinates). These include minima (whether relative or global), coinciding with reactants, products, and intermediates; as well as transition states (also known as saddle points).

There are two types of stationary points, each with their own definitions depending on the curvature of the potential energy surface at these points. If all of the eigenvalues of the Hessian matrix (second derivatives of the energy with respect to nuclear coordinates) are positive, the stationary point is a minimum. If there is one negative curvature, the stationary point is a transition state (a saddle point on the PES). Because vibrational frequencies are essentially the square roots of the curvatures, a minimum has all real frequencies, and a saddle point has one imaginary vibrational "frequency". This is how a frequency calculation helps to confirm a structure is either at a minimum or transition state.

Exercise 1: Reaction of Butadiene with Ethylene

Figure 2. Reaction scheme between butadiene and ethene

Butadiene and ethene react via a [4+2] cycloaddition to form cyclohexene. For the reaction to occur, the electrons must move between orbitals of the same symmetry; symmetry must be conserved. The orbitals in the product will also undergo the same symmetry operations as the reactants.

Figure 3. MO diagram of Diels-Alder reaction between butadiene and ethene

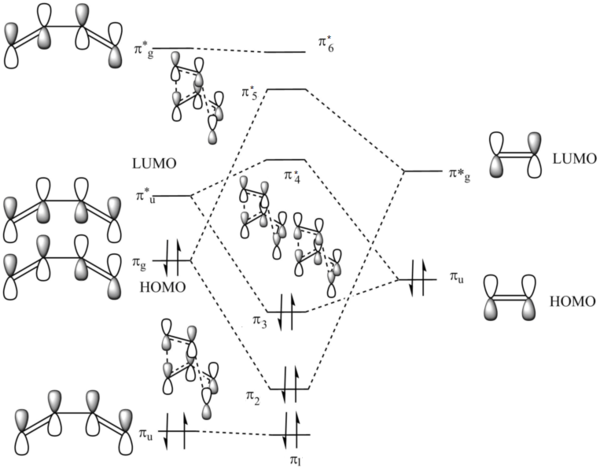
MO Analysis

According to the results of the Gaussian calculations, the HOMO of the transition state is formed from the LUMO of the ethylene and the HOMO of the butadiene, both of which have the π_u symmetry. A Diels-Alder reaction favours the interaction between the HOMO of diene and the LUMO of the dienophile due to a smaller energy gap and better orbital overlap resulting from attaching an electron withdrawing group to the dienophile substrate that raises energy of its LUMO. The small energy gap can be further enhanced by making the diene substrate more electron-rich that lowers the energy of its HOMO.

The overlap integral is zero for the interactions labelled π3 and π*5 and non-zero for interactions labelled π2 and π*4.

The four MOs produced in the TS are π*5, π*4, π3 and π2.

Molecule	Orbital	MOs	Symmetry
Butadiene	HOMO		g
butadiene	LUMO		u
Ethene	HOME		u
Ethene	LUMO		g
Transition State	HOMO		Symmetric
Transition State	LUMO		Asymmetric
Transition State	2nd HOMO		Asymmetric
Transition State	2nd LUMO		Symmetric

C-C Bond Analysis

Carbon-Carbon σ bonds are longer than π bonds. The bond length between C1-C2 and C3-C4 increase as they transform from π to σ only bonds in the reaction. The C2-C3 bond length shortens due to formation of a π bond. The C5-C6 bond lengthens as it transforms from a σ to a π bond. A ring system results in slightly shorter C-C bonds than alkanes would. The bond distances of the forming bonds C1-C6 and C4-C5 decrease to values corresponding to those of σ bonds. The Van der Waals radi for carbon is 1.70 angstroms. The length of bonds C1-C6 and C4-C5 at the transition state are less than twice the Van der Waals radius which indicates that a bond a forming. The typical sp³ and sp² bond lengths are 1.54Å and 1.47Å respectively.

Molecule	Bond Length (Å)
	C1-C2=1.33505 C2-C3=1.46832 C3-C4=1.33586
	C5-C6=1.32705
	C1-C2=1.37967 C2-C3=1.41123 C3-C4=1.37956 C4-C6=2.11482 C6-C5=1.38160 C5-C1=2.11469
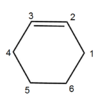
	C1-C2=1.50045 C2-C3=1.33754 C3-C4=1.50060 C4-C6=1.54015 C6-C5=1.54091 C5-C1=1.53869

Literature C-C bond distances

Transition State Analysis

File:TSFINALIRC.gjfThe vibration in Figure 4 illustrates the one unique negative and imaginary vibration frequency at the transition state (TS). As mentioned in the introduction, vibrational frequencies are essentially the square roots of the curvatures. The square root of a negative value is imaginary which is why the frequency at -948.91 cm^-1 is imaginary.

The vibration shows that the formation of the 2 new bonds between butadiene and ethene is simultaneous and therefore synchronous. The vibration shown is figure 5 is the first positive vibration which is not involved in bond making, it is asynchronous.

Figure 4: Negative transition state vibration frequency at 948.91 cm^-1

Figure 5. First positive transition state vibration frequency at 145.04 cm^-1

Exercise 2:  Reaction of Cyclohexadiene and 1,3-Dioxole

Figure 6. Reaction Scheme

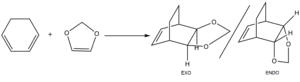
The Transition States

	Endo	Exo
Negative Imaginary Vibration

(These aren't your images, and aren't even the right system! Tam10 (talk) 14:09, 13 December 2016 (UTC))

Molecular Orbitals

Molecule	Orbital	MO
1,3-Dioxole	HOMO
1,3-Dioxole	LUMO
Cyclohexadiene	HOMO
Cyclohexadiene	LUMO
ENDO TS	HOMO
ENDO TS	LUMO
ENDO TS	2nd HOMO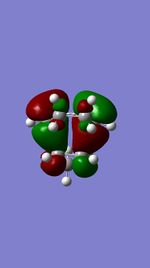
ENDO TS	2nd LUMO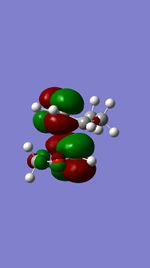
EXO TS	HOMO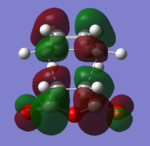
EXO TS	LUMO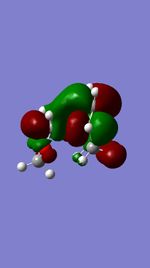
EXO TS	2nd HOMO
EXO TS	2nd LUMO

(You're selecting the last frame for MOs. The code worked before because they were optimisation calculations. These are opt+freq which have frames for each vibrational mode after the optimisation. You need to select the last optimisation frame eg 62 for the first one Tam10 (talk) 14:09, 13 December 2016 (UTC))

(Some of these images aren't yours and aren't relevant to the question! Tam10 (talk) 14:09, 13 December 2016 (UTC))

As shown in the table on the above, the HOMO of both transition states have π_g symmetry while the LUMO of both transition states have π_g symmetry as well because in both cases, these orbitals are resulted from the overlapping between the HOMO of cyclohexadiene and the LUMO of 1,3-Dioxole, both of which contains π_g symmetry. This is what as expected from a normal demand Diels-Alder reaction. 

(These symmetries require a centre of inversion which isn't present in the TSs. Tam10 (talk) 14:09, 13 December 2016 (UTC))

Thermochemistry Analysis

Geometry	Reactants (kJ/mol)	TS (kJ/mol)	Product (kJ/mol)	(kJ/mol)	(kJ/mol)
Endo	0	+165.35	-63.35	+149.68	+77.42
Exo	0	+155.85	-67.25	+156.98	+72.68

The thermodynamically favourable product is therefore the exo product, whereas the endo product is kinetically favourable.

Exercise 3: Diels-Alder vs Cheletropic

Transition State Analysis

	Endo	Exo	Cheletropic
IRC
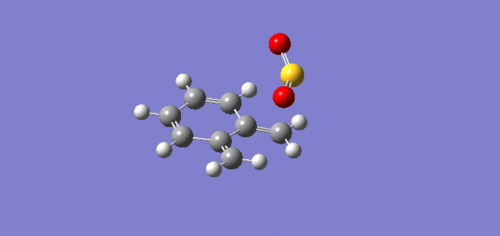
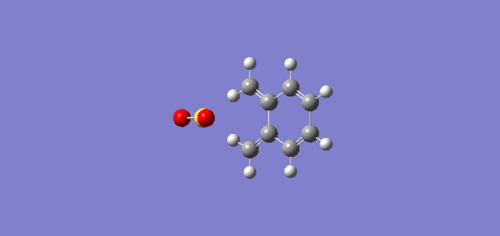
Reaction Profile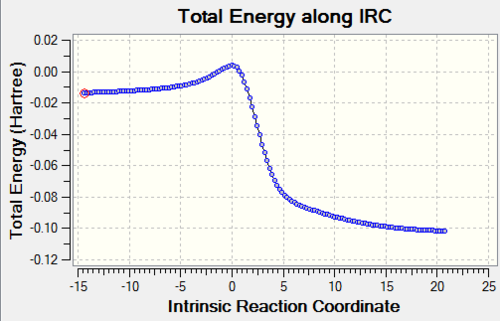

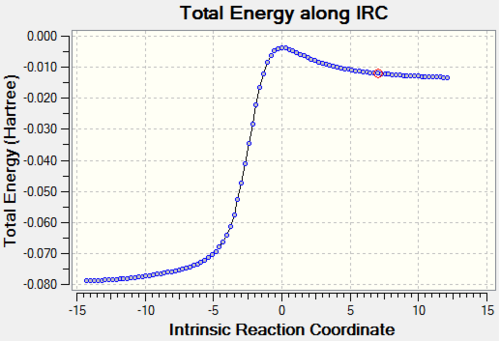
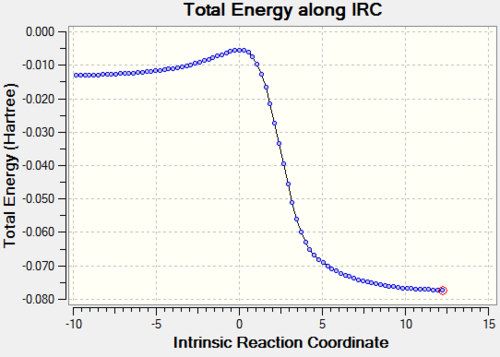
(Exo and endo are the wrong way around Tam10 (talk) 14:09, 13 December 2016 (UTC))

(These images are duplicates from this page Tam10 (talk) 14:09, 13 December 2016 (UTC))

The above table shows that the Exo and Cheletropic reaction IRC path was computed from the reactants to the products resulting in the path starting from lpwer energy than the end. However, for the Endo path, the IRC path was computed from the products to the reactants, resulting in a path which starts higher in energy than the end.

Thermochemistry Analysis

Geometry	Reactants (kJ/mol)	TS (kJ/mol)	Product (kJ/mol)	(kJ/mol)	(kJ/mol)
Endo	0.087456	0.090580	0.021748	0.002784	-0.065685
Exo	0.083420	0.091989	0.021445	0.008658	-0.063024
Cheletropic	0.071102	0.099043	0.000050	0.027856	-0.070984

(These energies are not in kJ/mol! Tam10 (talk) 14:09, 13 December 2016 (UTC))

The reactions between xylylene and SO₂ are exothermic and have negative reaction energy. Zylyene is extremely unstable therefore it has a high free energy. For all reactions the transition state has the highest energy and the product has the lowest energy. All three reaction profiles look similar to that of Figure 1. However, the difference, as explained above, is that the endo products are thermodynamically favoured, as the products lie lower in energy, whereas this is not the case for the other two.

(No, this doesn't match the data you've given. Cheletropic is clearly the thermodynamically favourable Tam10 (talk) 14:09, 13 December 2016 (UTC))

It is evident that the Cheletropic reaction has the highest activation energy and the endothermic Diels-Alder reaction has the lowest activation energy. This suggests that the endothermic reaction is the most kinetically preferred.

It can also be be seen that during the course of the reaction in all three reactions an aromatic 6 membered ring is formed from a diene. This is one of the causes for the stability of the product.

(No reaction profile Tam10 (talk) 14:09, 13 December 2016 (UTC))

Conclusion

In conclusion, Gaussian calculations confirmed a proposed MO diagram for the formation of the transition state and demonstrated that the reaction is an example of a standard Diels-Alder reaction. An IRC calculation showed that the bonds form synchronously due to the lack of substituents and therefore steric hinderance.

Furtheremore, MO analysis confirmed the assumption that this reaction would also be a standard Diels-Alder reaction due to an electron deficient dienophile and an electron rich diene, and furthermore it demonstrated that there is substantial secondary orbital interaction in the transition state HOMO of the endo- adduct. This concluded that the endo product would be the major product of the reaction as long as it was conducted under kinetic control. However analysis of the Gibbs Free Energy suggested the endo-product was the thermodynamic product and that the exo- product would not form spontaneously at all.

In addition, an IRC concluded that in all three cases calculated in exercise 3 there is delocalisation of electrons into the aromatic ring of xylelene around the TS stage of the reaction due to its high level of instability. Out of the two adducts the energy profiles suggest the endo product is the major product due to a smaller activation energy and larger reaction energy. This can be attributed to secondary orbital interactions not physically possible in the exo product.

Overall, using computation chemistry, in particular Gaussian, we are able simulate reactions without physically having to do any experiments. The benefits of this are quite simple, quick, easy, cheaper and in come cases, even more accurate.