Rep:Mod:Model 2 CS90
Module 2: Bonding (Ab initio and density functional molecular orbital)
Introduction
Please take into account the following accuracies for the different parameters:
1.) The energy has an error of ≈ 10 kJ/mol = 3.808x10-3 Hatree
2.) The dipole moment is accurate to 2 decimal places
3.) Fequencies in wavenumbers have an error of about 10%, because of a harmonic approximation used for vibrations that are actually anharmonic.
4.) Bond distances are accurate to ≈ 0.01 Å
5.) Bond angles are accurate to ≈ 0.1°
Gaussian 09W is used to perform all the calculations, whereas GaussView 5.0 is used to create, edit and show all the files that were generated by Gaussian.
BH3
Optimisation
Firstly, the BH3 molecule was drawn in GaussView. Then, bonds were manually set to 1.5A by clicking on "modify bond" and setting first atom as fixed and changing the bong length to a desired value. Finally, this molecule was then optimised.
In optimisation, firstly a given position of the nuclei is assumed and then the Schrodinger equation is solved for the electronic density and the energy. This part is called a SCF part. Secondly a position of the nuclei is then solved, which is the OPT part of the calculation and is much more complex. The nuclei move and the SCF cycle repeated at each geometry. The geometry with the lowest energy is then chosen.
The following settings were used:
# opt b3lyp/3-21g geom=connectivity
Where b3lyp is the method (using DFT calculations) and 3-21g is the basis set used in this optimisation.
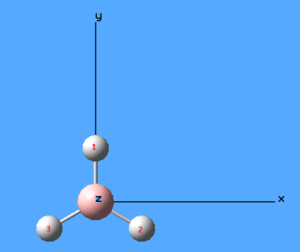
The summary of the BH3 optimisation calculation is shown in Table 1 and optimised BH3 can be seen in Figure 1.
Figure 1:Optimised BH3 molecule
 | ||||
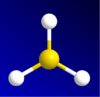Table 1:Summary of BH3 optimisation
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 3-21G |
| E(RB+HF-LYP) | -26.462 a.u. |
| RMS Gradient Norm | 0.000 a.u. |
| Imaginary Freq | - |
| Dipole Moment | 0.00 Debye |
| Point Group | D3H |
| Job cpu time | 16.3 seconds |
In order to make sure the calculation was successful, i.e. the optimisation has converged a .log file was checked, which proved all items have converged (Figure 2).
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000022 0.001800 YES RMS Displacement 0.000015 0.001200 YES Predicted change in Energy=-1.886451D-10 Optimization completed. -- Stationary point found.
Firstly all calculations were run on the computer and then on the SCAN supercomputer in order to obtain a D-Space link, which can be seen here:DOI:10042/to-7946
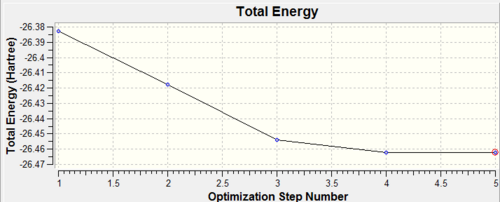
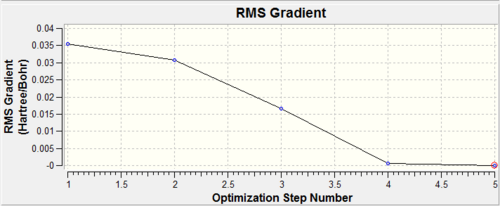
It is interesting to look at how the molecule has changed during different stage of optimisation. This can be seen in the Figure 3 together with graphs, which show the energy of optimisation and the RMS gradient (Figures 4 and 5).
Figure 3: Showing 5 steps of BH3 optimisation
aaaaaaaaaaa
1aaaaaaaaaaaaaaaaaaaaa
2aaaaaaaaaaaaaaaaaaaa
3aaaaaaaaaaaaaaaaaaaaaa
4aaaaaaaaaaaaaaaaaaa
5
Figure 3: A graph of energies at 5 different stages of BH3 optimisation
Figure 4: A graph of RMS gradient at 5 different stages of BH3 optimisation
Even though a convergence was accomplished, it is not necessary that it has converged to the right minimum. That is why a vibrational analysis was done as well, which gives us an information if the convergence has been to a minimum (all vibrational frequencies have to be positive), or a maximum (one negative frequency). If it is found that more than one negative frequencies are found, a stationary point was not found and thus calculations have gone wrong.
Vibrational frequency
It is important to note that for frequency analysis, both method and basis set have to be the same. This is because a minimum for this method is not necessarily a minimum on the potential energy surface calculated using different method or basis set. It is most likely that in the case of not having the same methods, negative frequencies would be obtained and thus suggesting that it has converged to a maximum instead of minimum. This "rule" is true in general, so it is important to remember energies, frequencies and other calculations can only be compared when using the same method and basis set.
Therefore, a DFT calculation with B3LYP method and 3-21G basis set was performed on the optimised BH3 molecule.
A summary of this calculation can be seen in Table 2
Table 2: A Summary of vibrational analysis of optimised BH3
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 3-21G |
| E(RB+HF-LYP) | -26.462 a.u. |
| RMS Gradient Norm | 0.000 a.u. |
| Imaginary Freq | 0 |
| Dipole Moment | 0.00 Debye |
| Point Group | D3H |
| Job cpu time | 19.0 seconds |
The same total energy of the frequency analysis and optimisation confirmed the calculations were performed on the correct file.
Bond distortions for this molecule were found to be: -0.6560, -0.0171, -0.0021, 20.2021, 21.4874 and 21.4974 cm-1 The more accurate the method the closer to zero these frequencies are. Since the low level method was used in this case, these valuse are not very close to zero, however the biggest "zero" frequency is still 2 magnitudes smaller than the lowest frequency of vibration, which is considered to be OK. Visualised vibrations and frequency values are shown in Table 3 and animations can be seen by clicking on the buttons.
Figure 5: Cartesian axes on BH3 molecule
Table 3: Summary of BH3 frequency calculations
| Animation of Vibrations 1-6 | Frequency/cm-1 | Intensity | Symmetry | Description of a vibration |
 |
1146 | 93 | A2" | All 3 hydrogens move with the same motion and in the same direction (out-and-in the plane – Z axis) but opposite boron, i.e. when hydrogens go one way, the boron moves the other, whereas it is still on the same axis as hydrogens – Z. Centre of Mass of the molecule thus does not change overall. Please note that molecule is rotated in the picture (left), simply due to clearer presentation of vectors, so axis set and molecule orientation in Figure 5 has to be looked at in order to represent a correct Z-axis. |
 |
1205 | 12 | E' | The hydrogen labelled 1 moves with the boron (Y-direction) whilst the other two hydrogens move so that one H-B-H angle is getting smaller at the same time as the other two angles are getting bigger. As boron moves the opposite way again (it is counteracting), the centre of mass does not change overall. |
 |
1305 | 12 | E' | This vibration is sort of a “rocking”-type, where the angle between hydrogens 2, 3 and boron does not change. This is achieved by hydrogen 2 moving up-right and down-left and hydrogen 3 moving down-right and up-left at the same time, respectively. Boron is moved only by a small amount and the hydrogen 1 counteracts the other two hydrogens by moving left and right in X direction. Centre of mass is constant. |
 |
2593 | 0 | A1' | This is a completely symmetric vibration where all B-H bonds stretch symmetrically at the same time, whilst the boron stands “still”. Again, centre of mass is constant. |
 |
2731 | 104 | E' | A bond between boron and hydrogen 1 is constant and the other two bonds stretch and contract asymmetrically to each other (one goes up and left whilst the other goes down and left). Boron and hydrogen 1 move by a small amount to counteract the other two stretches and so keep the centre of mass constant. |
 |
2731 | 104 | E' | The boron - hydrogen 2 and 3 bonds stretch symmetrically at the same time, whilst the bond of boron with hydrogen 1 stretches asymmetrically to the other two. Boron only moves by a small amount to keep the centre of the mass constant. |
Frequencies are all positive, thus the optimised structure truly was an energy minimum. One must not just blindly accept the results computer gives, however in this case calculations make sense and the calculated geometry(trigonal planar) is the expected structure. The boron-hydrogen bond length was calculated to be 1.19A and the B-H-B angle 120°o. As it is not always possible to say whether the bond length is "correct" or not, it can just be evaluated if it is reasonable or not. Since the literature value of B-H bond in a BH4- was found to be 1.21A[1], the calculated bond is reasonable.
IR
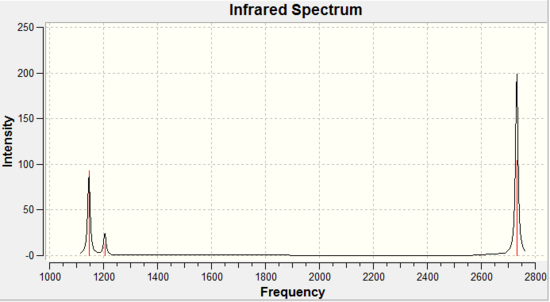
The IR analysis was performed and the following spectrum is obtained:
Figure 6: IR spectrum of optimised BH3 molecule
It is observed only 3 peaks are seen and not 6 as there are 6 vibrations. This is due to the following reasons:
For vibration modes 2 and 3, they are degenerate. This can be seen from the energy as they are the same, meaning they occur at the same frequency. Also, their symmetry label is e', which gives us information about degeneracy. Thus peak at 1205 cm-1 is due to two, degenerate vibrations.
This leaves us with 4 other vibrations. Vibration modes 5 and 6 are also degenerate (due to the same reasons as above) and so the peak at 2731 cm-1 is due to these two degenerate vibrations.
However, the vibrational modes that do not give a change in molecular dipole moment over the vibrvation will have a transition dipole moments equal to zero, which means that those vibrational modes are not infrared active.
For a vibration 4, one would expect this is an IR inactive vibration since it is totally symmetric and there is no change in dipole moment.
Thus there is one more peak left at 2593 cm-1 giving us a total of three IR peaks.
Molecular Orbitals analysis
Firstly, in order to predict what molecular orbitals should look like, a molecular orbital diagram was produced. When calculating MOs, the energy of the optimised BH3 molecule was calculated, retaining the method and basis set - DFT-B3LYP, 3-21G with a full NBO setting.
The following steps were performed and taken into account:
1.) Using a representation table, reduction and projection formula for fragment orbitals of H3
2.) Since hydrogen and boron have a similar electropositivity, their energy is similar and thus the energies in the MO graph are of similar height.
3.) Orbitals are mixed according to their symmetry labels - only orbitals of the same symmetry can interact and can do that only once.
4.) Mixing of secondary orbitals with the same symmetry usually occurs, however in this case it is probably not relevant as there are no orbitals of the same symmetry that could mix.
4.) S orbitals overlap much better than p and so the bonding and the anti-bonding orbitals are more stabilised and destabilised, respectively.
It is hard to tell if 2e' or 3a1' is lower energy, however due to the reason stated in point 4.) above I would predict that 3a1' might be more destabilised than 2e'. The MO diagram can be seen in Figure 7.
Figure 6: Molecular orbital diagram of BH3 together with "real", calculated MOs
Table 3: Orbitals and their energies of BH3
| Orbital | Orbital energies/a.u. |
| 1a1' | -7.576 |
| 2a1' | -0.705 |
| 1e' | -0.498 |
| 1a2 | -0.076 |
| 2e' | 0.322 |
| 3a1' | 0.345 |
It is clearly seen that the calculated molecular orbitals correlate nicely to the LCAO molecular orbitals. For unoccupied orbitals, however, it is slightly less clear, which is probably due to harder visualisation of the orbitals. From this it can be concluded that this molecular orbital theory is quite accurate. It gives all necessary information to understand the electron distribution and reactivity of the given molecule.
This molecule is very simple, though, and one can predict its MO structure, so this molecular orbital calculation is "more useful" in larger complexes where HOMO and LUMO (and other orbitals of interest) cannot be predicted by hand and so gives us information about which orbital is lower in energy and occupied and which one is not.
Natural Bond Orbital (NBO)
In this section, charge distribution is analysed. This calculation was done on the optimised BH3, where a delocalised MO picture is taken and a 2e-2c picture of bonding is given back.
The log file was opened and a summary of calculation can be seen in Figure 7.
Figure 7: A summary of NBO calculation
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
B 1 0.41527 1.99922 2.58551 0.00000 4.58473
H 2 -0.13842 0.00000 1.13816 0.00026 1.13842
H 3 -0.13842 0.00000 1.13816 0.00026 1.13842
H 4 -0.13842 0.00000 1.13816 0.00026 1.13842
=======================================================================
* Total * 0.00000 1.99922 5.99999 0.00079 8.00000
Natural Population -------------------------------------------------------- Core 1.99922 ( 99.9610% of 2) Valence 5.99999 ( 99.9999% of 6) Natural Minimal Basis 7.99921 ( 99.9902% of 8) Natural Rydberg Basis 0.00079 ( 0.0098% of 8) --------------------------------------------------------
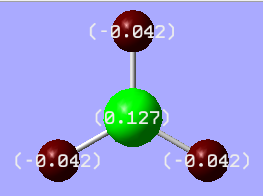
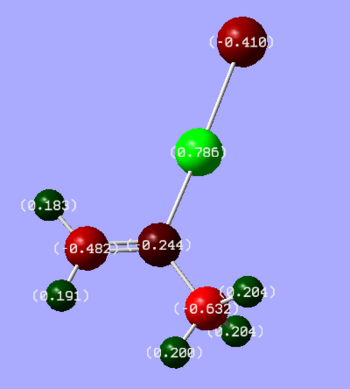
A picture of natural charges can be seen in Figure 8. Bright green colour shows highly positive charge and bright red colour shows a highly negative charge.
Figure 8: Charge distribution in BH3 where numbers are the NBO charges of the atoms
As expected from the Lewis structure, boron is proven to be highly positive, i.e. electron deficient (green).
In order to determine the bonding in the molecule, a log file is examined further.
Figure 9: A summary of NBO calculation - bonding
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.99882) BD ( 1) B 1 - H 2
( 43.08%) 0.6564* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.0000 0.0000
0.8165 0.0000 0.0000 0.0000
( 56.92%) 0.7544* H 2 s(100.00%)
1.0000 0.0001
2. (1.99882) BD ( 1) B 1 - H 3
( 43.08%) 0.6564* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 56.92%) 0.7544* H 3 s(100.00%)
1.0000 0.0001
3. (1.99882) BD ( 1) B 1 - H 4
( 43.08%) 0.6564* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 -0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 56.92%) 0.7544* H 4 s(100.00%)
1.0000 0.0001
4. (1.99922) CR ( 1) B 1 s(100.00%)
1.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000
5. (0.00000) LP*( 1) B 1 s(100.00%)
6. (0.00000) RY*( 1) B 1 s( 0.00%)p 1.00(100.00%)
From this, it can be seen that the first three NBOs are B-H where bonds contain 43% of boron contribution, which is sp2 hybridised (showing as 33.33%s and 66.67%p character), and 57% of hydrogen contribution, which are - of course - a 100%s character. The NBO number 4 is a core orbital at boron - 100% s character and does not participate in bonding (1s). The 5th NBO should be zero and not 100% as shown here, since it is expected this is a LUMO, i.e. empty orbital. This error is probably due to the low basis set used in this calculation.
Figure 10: A summary of NBO calculation - Second Order Perturbation of Fock Matrix in NBO basis
Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis
Threshold for printing: 0.50 kcal/mol
E(2) E(j)-E(i) F(i,j)
Donor NBO (i) Acceptor NBO (j) kcal/mol a.u. a.u.
===================================================================================================
within unit 1
4. CR ( 1) B 1 / 10. RY*( 1) H 2 1.37 8.62 0.097
4. CR ( 1) B 1 / 11. RY*( 1) H 3 1.37 8.62 0.097
4. CR ( 1) B 1 / 12. RY*( 1) H 4 1.37 8.62 0.097
This shows a mixing of molecular orbitals, however as seen before in MO section, the mixing is not relative in this case and thus this output does not give us much information. If any of the values in the E(2) column are greater than 20 kcal/mol, though they are important.
Finally, in the last section the energy and population or occupation of the B-H bonds, and the boron lone pair (B(LP*)) are recorded (Figure 11)
Figure 11: A summary of the NBO
Natural Bond Orbitals (Summary):
Principal Delocalizations
NBO Occupancy Energy (geminal,vicinal,remote)
====================================================================================
Molecular unit 1 (H3B)
1. BD ( 1) B 1 - H 2 1.99882 -0.59594
2. BD ( 1) B 1 - H 3 1.99882 -0.59594
3. BD ( 1) B 1 - H 4 1.99882 -0.59594
4. CR ( 1) B 1 1.99922 -7.48571 10(v),11(v),12(v)
5. LP*( 1) B 1 0.00000 0.82807
6. RY*( 1) B 1 0.00000 0.52622
7. RY*( 2) B 1 0.00000 0.52622
8. RY*( 3) B 1 0.00000 0.14582
9. RY*( 4) B 1 0.00000 0.61522
10. RY*( 1) H 2 0.00026 1.13006
11. RY*( 1) H 3 0.00026 1.13006
12. RY*( 1) H 4 0.00026 1.13006
13. BD*( 1) B 1 - H 2 0.00117 0.63344
14. BD*( 1) B 1 - H 3 0.00117 0.63344
15. BD*( 1) B 1 - H 4 0.00117 0.63344
-------------------------------
Total Lewis 7.99569 ( 99.9462%)
Valence non-Lewis 0.00352 ( 0.0440%)
Rydberg non-Lewis 0.00079 ( 0.0098%)
-------------------------------
Total unit 1 8.00000 (100.0000%)
Charge unit 1 0.00000
It is observed that there are 2 electrons in each boron-hydrogen bond, as one would expect.
TlBr3
Optimisation and pseudo potentials
As this molecule is more complex, a higher basis set has to be used than for BH3 molecule. This is because orbitals become more diffuse and polarizable as atom gets bigger and so this would affect the 3-21G basis set.
Therefore a LANL2DZ basis set is used, still with the same method DFT-B3LYP. This set uses the Los Alamos Effective Core Potential (ECP), ie. pseudo potentials, which is used for heavier elements. Also, a symmetry was set to D3h in this special case in order to obtain correct convergence and frequencies later on.
Figure 12:Optimised TlBr3 molecule
 | ||||
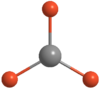Table 4:Summary of BH3 optimisation
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | LANL2DZ |
| E(RB+HF-LYP) | -91.218 a.u. |
| RMS Gradient Norm | 0.000 a.u. |
| Imaginary Freq | - |
| Dipole Moment | 0.00 Debye |
| Point Group | D3H |
| Job cpu time | 28.0 seconds |
Vibrational frequency
Again, it has to be confirmed that the minimum was attained. A frequency analysis was done on the optimised structure where the method and basis set were kept the same (DFT-B3LYP, LANL2DZ), as for the BH3 molecule (and any molecule for that matter). A summary of frequency calculation is shown in Figure 13.
Table 5:Summary of TlBr3 frequency calculation
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | LANL2DZ |
| E(RB+HF-LYP) | -91.218 a.u. |
| RMS Gradient Norm | 0.000 a.u. |
| Imaginary Freq | 0 |
| Dipole Moment | 0.00 Debye |
| Point Group | D3H |
| Job cpu time | 24.0 seconds |
The low frequencies were checked in .log file and found to be: -3.4213, -0.0026, -0.0004, 0.0015, 3.9367 and 3.9367 cm-1.
The lowest real normal mode is 46 cm-1 - an order of magnitude smaller than the lowest real frequency, which is OK. Vibrational frequencies of optimised TlBr3 molecule can be seen in Figure 13.
Figure 13:A summary of TlBr3 frequency calculations
| Vibrations 1-6 | Frequency/cm-1 | Intensity |
|
46.43 | 3.7 |
|
46.43 | 3.7 |
|
52.14 | 5.8 |
|
165.3 | 0 |
|
210.7 | 25 |
|
210.7 | 25 |
Output (log) file was checked for any negative frequencies. Only positive frequencies were found meaning the correct minimum was reached. The bond length of Tl-Br was calculated to be 2.65A and the bond angle of Br-Tl-Br 120°. This is a reasonable result since a literature value of Tl-Br bond was found to be 2.51A [2]
In the end, let's discuss what a bond actually is.
Although there are around 118 elements in the periodic table, it is obvious that there are more substances in nature than just 118 pure elements. This is a "consequence" of a chemical bonding. Atoms react which each other in order to form new compounds, where their total energy is lowered, making them more stable. There are several bonds such as covalent and ionic and the important part is that electrons are shared. A bond would not exist without electron sharing, that is also why some elements are electron-seeking (electrophiles) and the other like to donate their electrons. All that to obtain a satisfactory energy and thus a desired number of electrons to complete their valence shell.
So my definition of a bond would probably be that a bond is a cloud of shared electrons from an electron-deficient and electron-rich atom which, when come together, form a stable compound and their "need" for completing valence shell is satisfied. The bond is an equilibrium of "satisfactory" interactions, so it is not too long as if the atoms were too far apart, they would not interact and form a stable compound. Also, is is not too short as electrons repel if they are close to each other. So a stable bond is somehow in the middle of these two extremes.
It was observed that Gaussview sometimes "deletes" bonds between certain atoms, such as Cl and P atoms in this experiment. It does not actually delete them, they are just not visible, but they are still there. This is probably due to the fact that Gaussview has some sort of "fixed" value of how long a bond should be and when this value is exceeded it simply does not show the bonds. However the important part to note here is that bonds are present they are just not drawn.
Mo(CO)4L2
In the second year inorganic synthesis laboratory, cis- and trans- isomers of Mo(CO)4(PPh3)2 were prepared. There were found to be 4 carbonyl bands for cis and 1 band for the trans complex. Thus this is what is expected to be seen in our calculation analysis.
Since calculating the full molecule is too computationally expensive (large PPh3 groups), the phenyl rings are replaced with the less computationally demanding Cl atoms, which are sterically quite big and have shown to have a similar electronic contribution to the bonding as Ph too.
This sort of approximations are quite common in computational chemistry.
Firstly, a DFT-B3LYP method of optimisation was used with a low level basis set and pseudo-potential like LANL2MB to obtain the rough geometry right, together with loose convergence criteria (opt=loose in the "Additional keywords" box). This convergence relates to the first derivative of the energy. If the normal convergence criteria is used the limit sets are more accurate than the method used and the calculation might not converge to the right minimum.
After obtaining a rough optimisation for both isomers, the same method was performed using LANL2DZ pseudo-potential and basis sets using the normal optimisation criteria and with addition of int=ultrafine scf=conver=9.
At this point, Dr. Hunt has already searched over the rotational profile and worked out a good starting point that will get give us the right minima. So the following structres were built and then optimised using the mentioned method:
1.) Cis isomer has one Cl pointing up parallel to the axial bond, and one Cl of the other group pointing down.
2.)Trans isomer has both PCl3 groups eclipsed and one Cl of each group lies parallel to one Mo-C bond.
A summary of calculations can be seen in Figure 14.
Table 6: A summary of optimisation calculation using LANL2MB basis set
| Trans | Cis | |
| File Type | .log | .log |
| Calculation Type | FOPT | FOPT |
| Calculation Method | RB3LYP | RB3LYP |
| Basis Set | LANL2MB | LANL2MB |
| E(RB+HF-LYP) | -617.522 a.u. | -617.525 a.u. |
| RMS Gradient Norm | 0.000 a.u. | 0.000 a.u. |
| Imaginary Freq | - | - |
| Dipole Moment | 0.00 Debye | 8.47 Debye |
| Point Group | C1 | C1 |
| Job cpu time | 22minutes 10.1 seconds | 10minutes 12.3 seconds |
Trans: DOI:10042/to-7939
Table 7: A summary of optimisation calculation using LANL2DZ basis set
| Trans | Cis | |
| File Type | .log | .log |
| Calculation Type | FOPT | FOPT |
| Calculation Method | RB3LYP | RB3LYP |
| Basis Set | LANL2DZ | LANL2DZ |
| E(RB+HF-LYP) | -623.576 a.u. | -623.577 a.u. |
| RMS Gradient Norm | 0.000 a.u. | 0.000 a.u. |
| Imaginary Freq | - | - |
| Dipole Moment | 0.30 Debye | 1.31 Debye |
| Point Group | C1 | C1 |
| Job cpu time | 53minutes 16.7 seconds | 1hour 11minutes 48.8seconds |
Trans: DOI:10042/to-7940 , cis: DOI:10042/to-7941
After each computation, a .log file was checked for the convergence, where it was found that all the items have successfully converged.
Both optimised molecules can be seen here:
Vibrational Frequency
In order to confirm the minima, again frequency calculation was performed. This can be seen in Table 8.
Table 8: A summary of vibrational frequency calculation using LANL2DZ basis set
| Trans | Cis | |
| File Type | .log | .log |
| Calculation Type | FREQ | FREQ |
| Calculation Method | RB3LYP | RB3LYP |
| Basis Set | LANL2DZ | LANL2DZ |
| E(RB+HF-LYP) | -623.577 a.u. | -623.576 a.u. |
| RMS Gradient Norm | 0.000 a.u. | 0.000 a.u. |
| Imaginary Freq | 0 | 0 |
| Dipole Moment | 0.30 Debye | 1.31 Debye |
| Point Group | C1 | C1 |
| Job cpu time | 30minutes 8.0 seconds | 31minutes 12.9seconds |
Trans: DOI:10042/to-7944 , cis: DOI:10042/to-7942
There were a lot of vibrations within the molecule, however their intensities were quite small. It was also noticed that all low frequency vibrations were due to Mo-P vibrating bonds. Thus it can be expected that those vibrations with very low frequency will occur spontaneously at a room temperature (298.15 K). It was found, however, that the intensities for C=O stretches were quite high and thus those have been analysed as they seemed to be the most important stretching parts of this molecule.
Table 9: Frequency calculations summary for the trans complex
| Animation of Vibrations | Frequency/cm-1 | Intensity | Literature/cm-1 |
| 1950 | 1475 | 1896 | |
| 1950 | 1467 | 1896 | |
| 1977 | 0.6013 | ||
| 2031 | 3.762 |
Table 10: Frequency calculations summary for the cis complex
| Animation of Vibrations | Frequency/cm-1 | Intensity | Literature/cm-1 |
| 1945 | 762 | 1986 | |
| 1949 | 1499 | 1994 | |
| 1958 | 633 | 2004 | |
| 2023 | 597 | 2072 |
No negative frequencies were found in the .log file, confirming the correct minima. It is also clear that in IR spectrum, four bands will be seen for the cis complex and one band for the trans complex, confirming the calculations in this experiment have been successful.
From the calculation above, the relative energies can be compared since the method and basis sets are the same, as well as the number of all other atoms. Thus, from this calculation it can be concluded that the trans isomer is more stable than the cis by 2.63 kJ mol-1. Probably there are both electronic and steric contributions to stability. In terms of sterics, in cis isomer a molecule would experience a bigger clash due to large Ph3 groups being next to each other, as oppose to trans isomer where the groups are 180° to each other and hindrance is minimised.
It can be seen from calculated bonds (Table 10) that in trans complex, all metal-carbon bonds are the same, whilst in cis complex they are different. This suggests there is some kind of interaction in cis-complex, which makes it more stable.
However, the energy difference is very small and one effect could easily override the other, so I would say that their energies are approximately the same and depends on environment and other factors which one is more stable at the time.
Table 11: Bond lengths and angles of the two isomers and their literature values
| Bond (length) | Trans | Cis | Literature[3] |
| Mo-C | 2.06 | 2.06 and 2.01 | 2.01 |
| C-O | 1.17 | 1.17 and 1.18 | 1.16 |
| Mo-P | 2.44 | 2.51 | 2.50 |
| Bond (angle) | |||
| C-Mo-C | 179.18 and 89.4 and 90.5 | 178.35, 89.01, 89.74 and 87.07 | 180 and 92.1 |
| P-Mo-C | 90.13, 89.88, 88.70 and 91.3 | 176.01, 89.41, 91.89 and 89.23 | 87.2 |
Calculated bond angles and lengths are reasonable compared to the literature values.
It can be concluded that the optimised structure is a sensible structure, giving us similar data as in literature.
"Fine-tuning" catalytic behaviour
It is suggested that there are ways of "fine-tuning" catalytic behaviour by stabilising the structurally more efficient isomer. The PR3 group in this case could be tuned in order to make one isomer more stable (to dominate).
The trans isomer would not be very hard to obtain, a bulkiness of the R group would be increased and as the steric clash in cis-isomer would be bigger, a trans isomer would be more stable and will be the major product. Obtaining the cis isomer is more difficult and the only way I could see stabilising it is by firstly putting sterically small R groups that would not clash between each other. But then we would need another stabilisation. Pi-stabilisation would probably be more difficult to obtain, since if putting aromatic systems in, that would increase the clash, however if we put enough groups in between P and a pi system, maybe a clash would be avoided and interaction would be favoured. However it would probably be less demanding and more favourable to have a very small group, which is able to interact such as hydrogens that might hydrogen-bond to the other group.
Mini Project: Grignard Reagents
I decided to investiage the grignard reagents, how different halides affect the molecule's reactivity and how electron rich R groups contribute to reactivity as well. This was then compared with the literature and the yield a reaction gave when using different grignard reagents. Hopefully my calculations will confirm the literature data by the end of this investigation. The following three structures have been investigated:
Figure 14: The structure of three different grignard reagents
Optimisation
Several optimisations were carried out, using DFT-BRLYP method with different basis sets: 6-31G, LANL2MB and LANL2DZ. It was concluded since the molecule is not very complex, a higher lever can be used in order to obtain more accurate results.
Table 12: A summary of different optimisations carried out on molecules 1, 2 and 3
| Basis set | Molecule 1 Energy/a.u. | Molecule 2Energy/a.u. | Molecule 3Energy/a.u. | D-space |
| 6-31G | -818 | -2929 | -2889 | DOI:10042/to-7963 , DOI:10042/to-7964 , DOI:10042/to-7960 |
| LANL2MB | -172 | -170 | -130 | DOI:10042/to-7961 , DOI:10042/to-7962 , DOI:10042/to-7958 |
| LANL2DZ | -174 | -172 | -131 | DOI:10042/to-7955 , DOI:10042/to-7957 , DOI:10042/to-7959 |
It cannot be described much about optimisation, since molecules are different and so relative energies cannot be compared. This is just to show how calculations proceeded and which energies it gave. The only thing that can be taken from this is that energies for the last two basis sets are very similar, which is expected as they are similar basis sets, which are quite different from the 6-31G one.It was decided that LANL2DZ basis set will be used in other calculations, as it should give more accurate results.
In order to confirm minima, frequency analysis was carried out.
Vibrational Frequency
Only first 10 frequencies were analysed as those seem to be the most interesting, involving vibration of Mg-Cl bond. However for Mg-Br bond (in both molecules), there seemed to be only 2 interesting vibrations involving halide. Other low intensity frequencies are due to carbon-hydrogen bond vibrations in the R group and are not particularly interesting at this point.
Table 13: A summary of frequency analysis of molecules 1, 2 and 3 using LANL2DZ basis set
| Frequency/cm-1 | Intensity | D-Space | |
| Molecule 1 | 41.55, 67.45, 102.3, 122.0, 194.8, 226.6, 250.0, 364.1, 443.8, 604.3 | 1.80, 6.20, 14.2, 38.5, 21.0, 1.70, 3.10, 26.0, 19.7, 53.8, respectively | DOI:10042/to-7954 |
| Molecule 2 | 138.4 (3rd vibration), 534.3 (10th vibration) | 35.0 and 35.2 | DOI:10042/to-7952 |
| Molecule 3 | 162.7 (3rd vibration), 524.6 (9th vibration) | 9.04 and 31.3 | DOI:10042/to-7951 |
Interesting vibrations involving Mg-halide bonds can be seen here:
It is interesting to see that intensities of frequencies are higher for Mg-Br bond in the alkane than Mg_Br bond in alkene. This is probably due to the fact that there is more electron density at the C=C bond in the Molecule 3. This C=C double bond is electron rich and attracts the electropositive Mg, making it less able to vibrate, i.e. it gives it less "freedom" to rotate and vibrate, which probably results in lower intensity vibration of the Mg-Br bond.
As all frequencies were found to be positive, this confirms the minima were reached and that calculations were successful.
NBO analysis
This is probably the most interesting part (together with MOs) of my investigation, since I want to see the effects of halide groups (highly electronegative!) and also electronegative R groups. It is predicted that chlorine substituents will be more electronegative than bormine, which will affect the electropositivity of Mg and electronegativity of R groups. Furthermore, due to a double bond in molecule 3, it is expected that this will make a magnesium much more electropositive than in the corresponding alkane molecule, due to having more electron rich environment. Calculations with the same method and basis sets as before were made and the following results have been obtained:
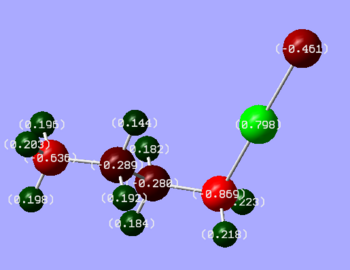
Figure 15: Showing charge distribution of the molecule 1, 2 and 3, respectively
It can be seen that the chlorine is more electronegative than a bromine, which consequently affects the magnesium being more electropositive in molecule 1 than molecule 3. The predicted theory has turned out to be correct.
One would expect that the first carbon (first from Magnesium), would be more electronegative in molecule 1, since chlorine is more electronegative, however it is very interesting to see that this is not the case. First carbon is slightly more electronegative in molecule 2, this is probably due to the fact that chlorine contracts the Mg-Cl bond more significantly than Mg-Br as Br is a larger atom and less polarisable than chlorine, which results in carbon being further away from the magnesium and thus being slightly less electronegative.
What is more, Mg is much more electropositive in alkene (as expected) due to rich double bond interaction.
Overall, the NBO analysis has confirmed most of the expected outcomes and this is a very good start for a molecular orbital analysis.
It is probably best to look at the Molecule 3 molecular orbitals as it involves double bonds, giving us more interesting MOs to analyse.
Molecular Orbitals
For molecular orbitals, it is hard to predict what exactly we want to see, however it is predicted that there will be lots of electron density on the R groups, due to double bond, which will interact with other groups, making Mg more electropositive than in the an alkane. It is also expected that in HOMO, most of the electron density clouds will be situated on the R group as this is the group which participates in the reaction.
Furthermore, as we learnt in 2nd year, when fragment orbitals are combined to give molecular orbitals, the contribution of each FO to MO is dependant on how close the FO is to the MO. So, the closer in energy, the higher contribution will have. And since electronegative orbitals are lower in energy than electropositive they will contribute more to the bonding orbital and less to the antibonding, where contribution is more from the less electronegative FO.
In our case, two different electronegative halides were used, Cl and Br. Thus, the less electronegative the element, the closer the HOMO and LUMO energy gap. So it is expected that HOMO-LUMO gap will be closer in energy for Molecule with a Br atom than for Molecule with a Cl atom.
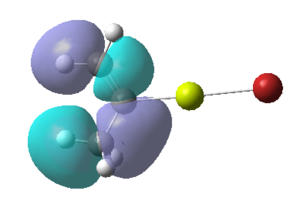
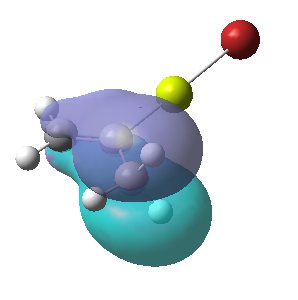
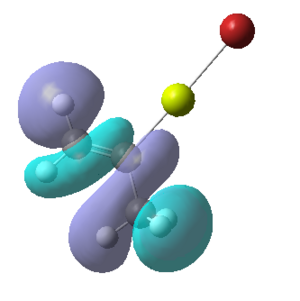
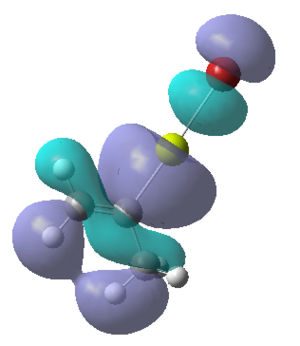
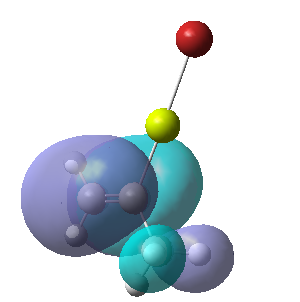
Figure 16:A summary of Molecular orbitals calculations for Molecule 3
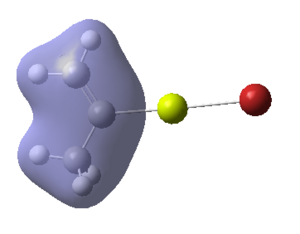
| Calculated Molecular Orbitals 1-16 up to LUMO (not includED) | Energy/a.u. |
|
-11.238 |
|
-11.230 |
|
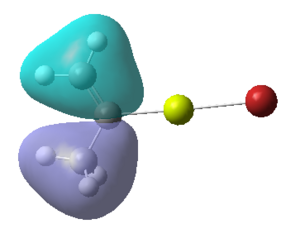
-11.228 |
|
-1.050 |
|
-0.947 |
|
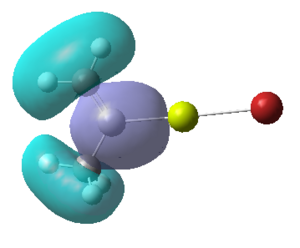
-0.929 |
|
-0.723 |
|
-0.617 |
|
-0.571 |
|
-0.565 |
|
-0.508 |
|
-0.439 |
|
-0.394 |
|
-0.393 |
|
-0.382 |
|
-0.354 |
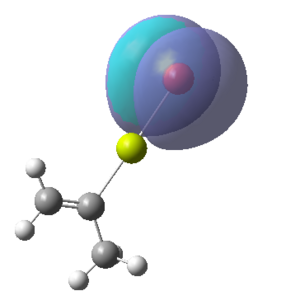
The energy difference between HOMO and LUMO was found to be 813.91 kJ/mol. It can be seen that indeed in the HOMO there is electron density on the R group, as it was expected. This is a very interesting information, which actually confirms the reactivity of the grignard reagents. R groups are nucleophilic and participate in the reaction (they are bonded to another reagent, where Mg-X is "removed" from the final product) and so is the most important part of this molecule.
It is fascinating to see that electron density is situated solely on the R groups in 11 out of 16 orbitals! This gives us much better visualisation of this molecule and its reactivity.
Another very good result can be seen when comparing HOMO-LUMO gap of all the molecules (pictures are not included since we are interested in the energy gap):
Molecule 1: 789.57 kJ/mol Molecule 2: 927.34 kJ/mol Molecule 3: 813.91 kJ/mol
As it can be seen, the HOMO-LUMO gap is smaller for Molecule 1 than for Molecules 2 and 3. This is excellent as it confirms expectations. This means that evaluation was correct and that different halides truly do affect the reactivity. It is somehow logical that Molecule 2 has a higher energy gap since Molecule 3 has more electron density around R group, making it more nucleophilic and susceptible to reaction.
This agrees excellent with the literature[4], where the yields correspond well to my calculations. In the article, it is stated that when a PhCH2CON(CH3)2 is reacted with a Grignard reagents - Molecules 2 and 3, the reaction with Molecule 3 (alkene) gives a better yield (52%) than the reaction with Molecule 2 (8%).
For Molecules 1 and 2, there seems to be contradiction to which one is a better Grignard (according to the literature[4]), as there are two yields reported within the same reaction:
Molecule 1: 38%, 40% Molecule 2: 69%, 18%
This suggests that the reagents are used in different environments, giving different yields.
This calculations showed that more electron rich R substituents truly are better Grignards. So increasing the nucleophilicity thus increases Grignard's reactivity. It would also be interesting to see what effect other large and electron rich R groups (such as aromatic systems) have on the whole molecule. Where is the "limit" of a good Grignard reagent and a too bulky reagents, since this also has to be taken into account when carrying out reactions. When increasing an electron density on R groups would increase its reactivity, it would probably have some other interactions that would make a grignard reagent eventually not stable and not suitable for reactions to be carried out. However, this is another topic, which we will not go into in this report. Nevertheless it would be a very interesting topic to research.
Conclusion
In the end of this module, it was appreciated how well computational analysis works. It is fascinating how a computer program can calculate so many different parameters and give us realistic values.
On the other hand, whilst this is a very good tool, one must not blindly accept the results the computer gives us. We have to continuously check if the calculations have gone to completion (have converged etc.), in order to obtain good results, as computer will not tell us if the result is wrong, it will just perform a calculation and give us the value.
So it was also learnt how to check for errors and understand each calculation, which I was never been able to do before.
The mini project was quite a success, it was not expected that such good results will be obtained. It gave interesting results, a lot was learned about reactivity of Grignards and gave a better understanding of the molecules themselves.
Overall it can be concluded that this module was a successful experiment, since aims have been fulfilled - to become a more knowledgeable computational chemist!
References
- ↑ M.R. Hartman, J.J. Rush, T.J. Udovic, R.C. Bowman and S.J. Hwang, Journal of Solid State Chemistry, 2007, 180, 1298-1305 DOI:10.1016/j.jssc.2007.01.031
- ↑ J. Glaser and G. Johansson, Acta Chemica Scandinavica, 1982, 36a, 125-135 DOI:10.1021/jp0124802
- ↑ G. Hogarth, T. Norman, Inorganic Chemistry Acta, 1997, 254, 167DOI:10.1016/S0020-1693(96)05133-X
- ↑ 4.0 4.1 A T. Imamoto, N. Takiyama, K. Nakamura, H. Hatajima and Y. Kamija; J. Am. Chem. Soc., 1989, 111, 4392-4398DOI:doi:10.1021/ja00194a037