Rep:Mod:MgOben14
The Free Energy and Thermal Expansion of MgO
Introduction
Thermal expansion is the change in shape, area or volume of matter in response to a change in temperature.[1] [2] The coefficient of thermal expansion describes this intrinsic property of materials (through normalisation with the V0 term), at constant pressure as given by the equation below, Equation 1[3].

Isotropic expansion is such that the rate of expansion is equal in all directions, and is more simple to model.[3] There are many significant applications for the modelling of this phenomenon which is discussed and presented here through the example of magnesium oxide, MgO. One such example is the the construction of any large structure where changes in dimension can occur due to temperature variations, engineers must account for this thermal expansion in its design and operation, though due to the often very large size of these structures, only a crude approximation is required. The choice of metals with minimal expansion coefficients for use in alloys in aerospace engineering is one example where precise understanding of this field is fundamental in enabling the safe and correct operation of the aircraft[4].
Aims of MgO Computational Lab
A simple model of atomic interactions were used to calculate the energy and vibrations of an ideal, non-defective and periodic crystal of MgO. In particular, phonon dispersion curves showed the crystal's vibrational energy structure.
The vibrational energies were then used to determine computationally the Helmholtz Free Energy of the crystal, once an ideal basis i.e. dimensions of the cell had been selected as an optimised function of accuracy and computational time. As the Helmholtz Free Energy is a property dependent on the temperature and volume, this then enabled the prediction of how the material expands when heated, through the computation of selected properties of the crystal, such as the lattice parameter and unit cell volume. The Quasi-Harmonic (or Lattice Dynamics, LD) and Molecular Dynamics (MD) approximations were compared for their accuracy in this modelling of the thermal expansion, alongside a comparison with the literature available[5].
Experimental
Tools in Use
The computational tools employed for the generation of the models used and for the running of simulations are listed below. The Linux operating system provided a suitable environment for numerical simulations. DL Visualize is a graphical user interface which served to run the molecular modelling code GULP.
- RedHat Linux
- DL Visualize
- GULP (General Utility Lattice Programme)
Methodology Used
The Quasi-Harmonic Approximation Model
The quantum mechanical Quasi-Harmonic Approximation model (alternatively known as the Lattice Dynamics Model) is used for the description of volume dependent thermal effects. It is based on the assumption that the Harmonic Approximation holds for each value of the lattice constant.[6] A purely harmonic model (as modelled by a parabola) is unable to adequately model thermal expansion because equilibrium distance would be independent of temperature (and as such no expansion would occur). Therefore, the phonon frequencies are allowed to become volume dependent, but such that for each volume, the harmonic approximation holds, hence termed quasi-harmonic.[6] It should be noted that the model does not account for any 'phonon-phonon' interactions however, and as such, anharmonicity is observed in the output of the calculations. For the purpose of these calculations, this is disregarded though will contribute to the error in the calculations, when compared to literature.
The Helmholtz Free Energy in the Quasi-Harmonic Model is given by Equation 2 below, (where F is Helmholtz free energy, E is the zero potential energy, T is temperature (K) ).
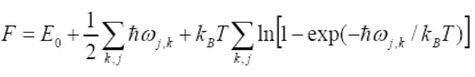
The Molecular Dynamics Model
The Molecular Dynamics model was employed in addition to to the Quasi-Harmonic Approximation discussed above to allow comparisons of the models, as presented in the Results and Discussion section. This is a classical mechanics model where vibration is represented as random motion. It makes use of Newton's Second Law of Motion (F = ma) to determine the force acting on an atom moving along its trajectory over a period of time. The model provides an alternative approach to the computation of thermodynamic properties. Its accuracy and applicability for the system under investigation is evaluated in the Results and Discussion section below.
Results and Discussion
Representing the MgO Structure
The output of the initial calculations provided the parameters of the MgO crystal. The cell can be represented both in terms of the primitive cell and the conventional cell, displayed in the Figures below.
The primitive cell is the smallest cell that can be used to describe the crystal structure: it is a rhombohedral structure consisting of 1 oxygen at the body centre and 8 x 1/8 Mg (each located on the corners of the shape), yielding a two atom cell. The output of the calculations is provided below.
bond angle 60.0000°
lattice constant 2.9783 Å
The conventional cell represents the FCC (face centred cubic) nature of the system more clearly. The output of the calculations yielded a lattice constant of 4.212 Å, which is in agreement with the published literature value.[5] It should be noted that the densities of these cells do not differ, the volume of the convensional cell is simply four times that of the primitive cell.

Phonon Dispersion Curves
The phonon dispersion curve was computed for the modelling of the vibrational energy structure of the crystal, as shown in Figure 2 below. The aim was to investigate how vibration affected expansion. The figure shows the relationship between the vibrational frequency of the phonon (ωk) and the wavevector k. It is periodic with a*=2π/a where a is the lattice parameter, and a* is the magnitude of the Brillouin Zone (the unit cell of the reciprocal lattice). A vibrational band is denoted by the term branch and these branches are observed in the figure below. The total number of branches is given by the product of the number of atoms in the primitive cell and the number of dimensions. For our primitive cell consisting of 2 atoms (as discussed in the section above), in 3 dimensions, 6 branches are observed.
The merging of branches that can be seen for MgO is due to reduction by symmetry and the resulting degeneracy of the vibrational modes. Optical and acoustic branches are exhibited for this crystal, as it has a primitive cell consisting of more than one atom, which gives rise to both coherent movements of atoms in the lattice out of their equilibrium positions (acoustic phonons) and out of phase movements (optical phonons)[7]. The optical modes have a non zero frequency at the centre of the Brillouin zone (denoted by Γ =(0,0,0)).

The frequencies of the bands at the single k point (as determined by overlaying with the Phonon Density of States graph, Figure 3 below) used in the 1x1x1 calculation were: 288.49, 288.49, 351.76, 351.76, 676.23, 818.82. For the degenerate vibrational modes, the density of states is greater, to indicate this.

The density of states (DOS), as shown in the figure above is the energy distribution of the system, i.e. the number of states at each frequency. In the subsequent section, greater grid sizes are investigated, in order to optimise the calculation in terms of accuracy and computational time. The one k point (taken arbitrarily by the software at 0.5,0.5,0.5 but represented in the phonon dispersion curve as at L (1,1,1) showing only a translation but leaving the model unaffected) is not sufficient for the accurate depiction of the DOS.
Grid Size Optimisation
The density of states of the vibrational energy levels (DOS) was studied to determine the required basis for the accurate modelling of the system. The Helmholtz free energy was taken at various grid dimensions (as detailed in both the figure and table below) in order to quantify the accuracy to which the calculations should be carried out. This was then evaluated against the expense of computational time in which the calculations were to be run. Examining grid sizes of equal dimensions in the x, y and z plane (1x1x1..2x2x2...64x64x64) yielded systems with a high degree of symmetry, reducing greatly the calculations needed to model this system, and thereby reducing computational time, which is advantageous when carrying out this work. Thus ultimately the computational time was not a significant factor in this optimisation process, each submitted calculation ran well within an acceptable period for the timescale of the lab (maximum 5 minutes for the longest). From the figures presented below, it can be seen than an increase in the number of unit cells used increases the resolution of the DOS because it takes into account more of the possible vibrations of the system.

To quantify the level of accuracy to which the above grid dimensions allow the calculations to be run, a physical parameter was extracted from each of the output log files, the Helmholtz free energy, presented in Table 1 below. With increasing grid dimension, there is an incremental decrease in the Helmholtz free energy, smaller at each step until the value is optimised.
| Dimensions | Helmholtz Free Energy (eV) |
|---|---|
| 1x1x1 | -40.330301 |
| 2x2x2 | -40.926609 |
| 3x3x3 | -40.926432 |
| 4x4x4 | -40.926450 |
| 5x5x5 | -40.926463 |
| 6x6x6 | -40.926471 |
| 7x7x7 | -40.926475 |
| 8x8x8 | -40.926478 |
| 16x16x16 | -40.926482 |
| 32x32x32 | -40.926483 |
| 64x64x64 | -40.926483 |
As can be seen, the 32x32x32 system is sufficient, as the value of the Helmholtz free energy is determined to a convergent value, there is no further benefit in increasing to 64x64x64. The 3x3x3 grid size would be sufficient to provide a calculation accurate to 0.1 meV, should computational time be limiting (for a less symmetric system, for example).
It is interesting to examine also how this optimisation process would have to be altered for other materials.Given three contrasting examples: an oxide similar to MgO (CaO), a zeolite (faujasite) and a metal (lithium), the variation in their lattice constants is an excellent starting point, due to the inverse relationship between the length of the unique Brillouin zone, a* as shown in Equation 3 below.
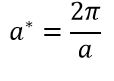
The literature lattice constants for the materials discussed above are presented in Table 2 below, where an approximate relative optimised grid size is given qualitatively, followed by a rationale in the discussion below.[8][9][10][11]
| Material | Lattice Constant, Å | Ideal Grid Size (relative to MgO) |
|---|---|---|
| CaO | 4.800 | similar to MgO |
| Faujasite | 24.638-24.650 | smaller than MgO |
| Lithium | 3.5107 | smaller than MgO |
As the CaO is of a similar sized lattice to MgO, a similar number of k points (and therefore grid dimensions) would be needed to provide the optimum output. The zeolite, faujasite, has a lattice constant much greater than MgO, and due to the inverse relationship discussed above, a much narrower Brillouin zone. This leads to a smaller grid size being sufficient for the sampling of the necessary number of k points for an accurate model.
Initially, it may seem that due to the smaller lattice constant of Li, and the reciprocal relationship, the grid size should be larger than for MgO (which would lead to long computational times). However, this is in fact not the case due to the difference in bonding present in the lithium metal (ionic) compared to magnesium oxide (covalent). The ionic nature of the Li bonds results in the presence of delocalized electrons, which in turn leads to less repulsion between the metal cations.[12] Thus a narrower energy band (a less disperse Density of States function) would be observed, and accordingly a smaller grid size would be adequate.
The Thermal Energy of MgO
The Quasi-Harmonic Approximation
The results of the optimisation with respect to the free energy computed within the quasi-harmonic approximation at a number of temperatures is presented and discussed in this section. This is quantified through the use of the Helmholtz free energy, as shown in Equation 4 below, with an entropic term that sums over all k-values so is a useful indication of accuracy.
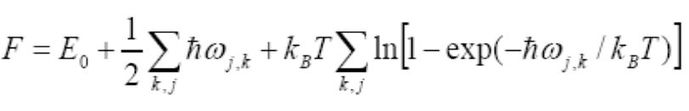
The charts below show the plot of the Helmholtz free energy (Figure 5 a)) as well as the lattice constant (Figure 5 b)) and cell volume against temperature (Figure 5 c)) for the temperature range 0 -1000 K in 100 K increments.

The trend in the variation of lattice constant is as expected: the greater the the temperature, the greater the thermal energy and therefore there is a larger average distance between the atoms. This is directly responsible for the same trend observed in the cell volume.
Within the temperature range 300-1000 K there is a linear relationship with temperature. A linear regression can be applied to this region, with the gradient of the curve showing the change in volume with respect to the change in temperature (at constant pressure, it is a solid and thus this can be assumed). Employing Equation 1 (see Introduction) for the thermal expansion coefficient, a value of 2.65442E-05 K-1 is obtained. This can be compared as to the literature value of 3.16E-05 K-1 (for the temperature range 303 - 1273 K) to produce an error of 16%. This error can be accounted to the approximations made in the Quasi-Harmonic model, however this is within an acceptable range. .
The linear trend stated above however does not accurately model the low temperature regime, where the thermal expansion shows deviation from linearity due to a degree of temperature dependence. The Helmholtz free energy computed at 0 K is denoted as the Zero Point Energy, which is effectively a residual energy arising from quantum mechanics.
This can be explained through examination of the underlying principles in the quasi-harmonic approximation model. As introduced in the Experimental section of the report, this is a quantum-mechanical based model that builds on the harmonic oscillator, however introduces anharmonicity to allow thermal expansion. This cannot happen in a purely harmonic system as the bond length cannot vary with the population of thermally excited states. The quasi-harmonic approach allows for the variation of bond length, and thus thermal expansion with the population of higher energy states as a result of greater thermal energy. Figure 6, showing the harmonic and anharmonic oscillator, illustrates this further.

In the upper limit of 1000 K the Quasi-harmonic approximation continues to be valid, due to the melting point of MgO being much greater than this, at 3125 K[12]. At that temperature, a change in the free energy trend would be expected, since it would no longer be a crystal structure, with vibrations but rather a much more disordered system. The Molecular Dynamics section below discusses this high temperature regime further.
The Helmholtz free energy decreases with increasing temperature and this can simply be accounted for using the thermodynamic definition of Helmholtz Free Energy, provided in the equation below (Equation 5).
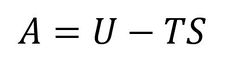
As can be seen from the equation, with an increase in temperature, the -TS term becomes increasingly negative, in addition to the increase in entropy due to the greater thermal disordering. The non-linearity once again arises from the quasi-harmonic approximation.
Molecular Dynamics Calculations
Following the quasi-harmonic calculations, an alternative approach was carried out for comparison. The molecular dynamics calculations model vibration as random motion, based on classical mechanics. The graph presented below in Figure 7 shows this, alongside a comparison to the LD approach. As can be seen from the plots, the MD approach is not accurate in the low temperature regime, though appears to converge to the quasi-harmonic approximation in the high temperature limit of this 300- 1000 K region. The discussion below provides rationale for the observed results and compares the thermal expansion coefficient, α obtained with literature.

The MD approach yields a thermal expansion coefficient of 3.1853E-05 K-1 (over the same 300-1000 K temperature range as above), which is a variation of less than 1% from the literature value stated above, thus in excellent accordance. The improved accuracy of the molecular dynamics model in this 300- 1000 K temperature range can be attributed to the fact that at these higher temperatures random motion due to thermal excitation is increasingly significant.
At temperatures below this, the model becomes increasingly inaccurate because there is less thermal motion. At 0 K, it is unable to provide an approximation - the thermal motion would be zero, rather than the zero-point energy that the LD model correctly predicts, showing the limits of the approach. Harmonicity and a quantum mechanical treatment is required here: due to intrinsic limitations imposed on the material, as expressed by the Heisenberg Uncertainty Principle, the molecular dynamics approach becomes invalid.
In the high temperature limit, the model would continue to work well, because in the melted state the system is very well described by random thermal motion. The model would predict a persistent thermal expansion of the volume, as the material changes from solid to liquid to gas (provided the thermal expansion coefficient were positive, which is not always the case, such as for pure water below 3.98 °C).[13]
The MD calculations made use of 32 MgO molecules (i.e. 64 atoms) which is much less than that for the Quasi-Harmonic calculations, but the greater increase in computational time required to run these calculations justifies this.
Conclusion
It can be seen from the discussion presented in the sections above that the two approaches (Quasi-Harmonic and Molecular Dynamics) implemented for the modeling of the thermal expansion of MgO are each more suited to the low and high temperature regions, respectively. To compare, a linear fit was made on the 300 - 1000 K region of both plots, to yield thermal expansion coefficients of 2.65442E-05 K-1 for the Quasi-Harmonic Calculations (16% error) and 3.1853E-05 K-1 (0.8% error) for the Molecular Dynamics calculations. The methodology utilised in each step was rationalised through the an explanation of the relevant theory and by considering the computational calculation process to identify where shortcuts (such as reduction in calculations due to symmetry) were possible. The use of other materials for such calculations were also explored, reaching the conclusion that both metals and large structures such as zeolites would suffice with smaller grid dimensions (and hence shorter computational times) than MgO, although for distinct reasons. To build further on the computational work, it would be of interest to model other structures, such as ice perhaps, which exhibit negative thermal expansion (NTE) in both very low (-200 °C) temperatures and also in its liquid form, when below 3.98 °C.[13]The cell size required for molecular dynamics could also be optimised for further work, as was done for the quasi-harmonic model.
References
- ↑ R. A. Schapery, J. Compos. Mater., 1968.
- ↑ P. Atkins and J. de Paula, Atkins’ Physical Chemistry, OUP Oxford, 10th edn., 2014.
- ↑ 3.0 3.1 K. V. K. Rao, AIP Conf. Proc., 1974, 17, 219–230.
- ↑ K. U. Kainer, Metal Matrix Composites: Custom-made Materials for Automotive and Aerospace Engineering, 2006.
- ↑ 5.0 5.1 C. Y. Ho and R. E. Taylor, Thermal Expansion of Solids, ASM International, 1998.
- ↑ 6.0 6.1 M. T. Dove, Introduction to Lattice Dynamics, Cambridge University Press, 1993.
- ↑ L. Saviot, B. Champagnon, E. Duval, I. A. Kudriavtsev and A. I. Ekimov, J. Non. Cryst. Solids, 1996, 197, 238–246.
- ↑ H. Zhang and M. S. T. Bukowinski, Phys. Rev. B, 1991, 44, 2495–2503.
- ↑ O. Madelung, U. Rössler and M. Schulz, Eds., in II-VI and I-VII Compounds; Semimagnetic Compounds, Springer Berlin Heidelberg, Berlin, Heidelberg, 1999, pp. 1–3.
- ↑ Clays and Clay Minerals, 197,3, Vol. 21, pp. 379-389
- ↑ S. H. Kellington, D. Loveridge, J. M. Titman, H. F. H. and A. B. L, K. G. and M. A, N. S. K, T. J. M. and K. S. H and V. H, J. Phys. D. Appl. Phys., 1969.
- ↑ 12.0 12.1 C. Kittel, Solid State Phys., 2005, 703.
- ↑ 13.0 13.1 K. Röttger, A. Endriss, J. Ihringer, S. Doyle and W. F. Kuhs, Acta Crystallogr. Sect. B Struct. Sci., 2012, 68, 91–91.
