Rep:Mod:Mengsha

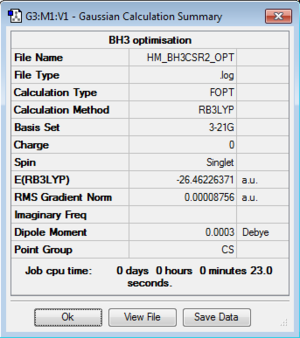
Day 1 BH₃ B3LYP/3-21G level

BH₃ Point Group: Cs

B3LYP/3-21G level

Optimisation log file here

Point group	Summary data	Convergence	Jmol
Cs		Item Value Threshold Converged? Maximum Force 0.000217 0.000450 YES RMS Force 0.000105 0.000300 YES Maximum Displacement 0.000919 0.001800 YES RMS Displacement 0.000441 0.001200 YES	optimised borane molecule

BH₃ Point Group: C1

B3LYP/3-21G level

Optimisation log file here

Point group	Summary data	Convergence	Jmol
C1		Item Value Threshold Converged? Maximum Force 0.000448 0.000450 YES RMS Force 0.000228 0.000300 YES Maximum Displacement 0.001674 0.001800 YES RMS Displacement 0.001108 0.001200 YES	optimised borane molecule

BH₃ Point Group: D₃H

B3LYP/3-21G level

Optimisation log file here

Point group	Summary data	Convergence	Jmol
D3H		Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000016 0.001800 YES RMS Displacement 0.000010 0.001200 YES	optimised borane molecule

When testing the point group of BH₃, it initially shows Cs which is not expected. This is because the quantitative information obtained from the program is not accurate enough to give the right symmetry based on the low level basis set 3-21G. The slight changes in the coordinates x, y and z will also make the BH₃ structure miss the D₃H symmetry. After symmetrising by enabling the point group to be D₃H, BH₃ finally achieved a perfect trigonal planar geometry with H-B-H bond angle 120.0°.

Day 2 Better basis set

BH₃: B3LYP/6-31G level

Optimisation log file here

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000017 0.001800 YES RMS Displacement 0.000011 0.001200 YES	optimised borane molecule

Optimised B-H bond distance: 1.19 Å

Optimised H-B-H bond angle: 120.0°

GaBr3: B3LYP/LANL2DZ level

Optimisation log file:DOI:10042/193792

Optimisation log file here

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000003 0.001800 YES RMS Displacement 0.000002 0.001200 YES Predicted change in Energy=-1.307745D-12 Optimization completed. -- Stationary point found.	optimised GaBr3 molecule

Optimised Ga-Br bond distance: 2.35 Å

Optimised Br-Ga-Br bond angle: 120.0°

Compared with the literature value^[1] of the bond distance of Ga-Br, 2.33-2.34 Å in a concentrated solution at room temperature, the optimised Ga-Br bond length is highly accurate under the computational method using a larger basis set LANL2DZ and pseudo-potentials.

BBr₃: B3LYP/6-31G(d,p)LANL2DZ i.e. GEN level using a mixture of basis-sets and pseudo-potentials

Optimisation DSpace DOI:10042/193795

Optimisation log file here

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000036 0.001800 YES RMS Displacement 0.000024 0.001200 YES	optimised BBr3 molecule

Optimised B-Br bond distance: 1.93 Å

Optimised Br-B-Br bond angle: 120.0°

Geometry Comparison of EX₃

Geometry data

	BH3	BBr3	GaBr3
r(E-X) Å	1.19	1.93	2.35
θ(X-E-X) degrees(º)	120.0	120.0	120.0

For the 3 compounds with varying central elements and ligands, they have same X-E-X angles under the accuracy to 1 d.p. but the bond lengths change in different ways with estimated values to 2 d.p.

Group 3 element B is small in size and electropositive while Br is large and very electronegative. The large differences in atomic size and electronegativity contribute ionic character to the B-Br bond, making it more easily broken than B-H. The B-Br bond is indicated to be longest and weakest among the 3 E-X bonds.

Compared with Br, H similarly needs one more electron to achieve its stable electronic configuration of the outer shell, but H is also much smaller and matches better with B in size than Br. It increasesthe orbital overlap between B and H atoms and therefore shortens the bond length of B-H. In addition, since Br is large in size, 3 Br atoms suffer from greater steric hindrance from binding together to the central B. In contrast, B in BH₃ is much more sterically available and this favours B to bond more strongly with H. So having H as ligand gives shorter B-X bond with larger dissociation energy than ligand Br.

B and Ga are both in Group 3, so they have same electronic configuration in valence shell. But Ga is lower down in the group, larger and less electronegative than B. The smaller difference in electrogenativity makes the bond distance between Ga and Br shorter, and Ga has more space to occupy 3 big Br atoms than B at the same time. Although Ga and Br are in the same period, which means the overlap of atom should be enhanced between two similar sizes. Ga is metal so the Ga-Br is more metallically bonded where Ga is partially positive and Br is partially negative. The Ga-Br bond is actually more polar than B-Br which experiences more effective orbital overlap and this makes Ga-Br longer and weaker than B-Br.

Discussion on the strength of chemical bonds^[2]

Positive and negative species in atoms are electrostatically attracted to form stable chemical bonds in substances. The species could be originally oppositely charged or they could be induced to have partial charges. Covalent and ionic bonds are both intramolecularly formed strong bonds. The covalent interaction is usually through the maximised overlap of two non-metal atoms by sharing the electrons between atomic centres. The high covalent character indicates small electronegativity difference between the comprised substituents. For example, single covalent N-N has medium bond energy 170 kJ/mol while the strong triple bond between nitrogens is 945 kJ/mol. Simply, the covalent bond dissociation energy increases with bond order. Ionic bonds involve the complete transfer of electrons from a metal atom to a non-metal, giving a pair of charged species as the two bonded atoms have large difference in electronegativity. For example, Na-Cl has a relatively high the lattice energy of 787 kJ/mol. The weak bonds are usually intermolecular attraction including weak London dispersion force and relatively strong hydrogen bonding. A typical N-H---O bond in vapour has enthalpy around 8 kJ/mol which is overall much weaker than ionic and covalent bonds.

Absence of bonds in Gaussview

The Gaussview provides the visulisation of molecules in a convenient way but Gaussview misses the bonds in some molecule structures. However, it doesn't mean the absence of bonds. The bonds actually exist, but it exceeds the defined bond distance which is based on organic molecules. Here we are concentrating on inorganic compounds which means their bond length in the Gaussview is longer than the set value when we draw it.

Day 3

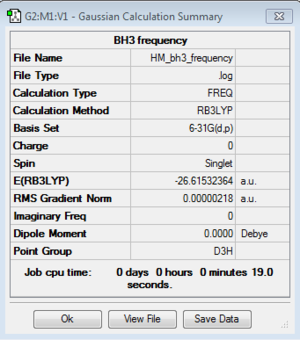
BH₃:B3LYP/6-31G(d,p)

Frequency file: here

summary data	low modes
	Low frequencies --- -6.1015 -6.0459 -0.0245 -0.0007 0.8219 7.5511 Low frequencies --- 1163.0065 1213.1605 1213.1607

Vibrational spectrum for BH₃

Wavenumber	Intensity	IR active?	Type
1163	93	yes	bend
1213	14	very slight	bend
1213	14	very slight	bend
2582	0	yes	stretch
2716	126	no	stretch
2716	126	yes	stretch

|

From the IR spectrum, there are only 3 vibrational peaks while 6 peaks predicted in the table. This is because the peak at wavenumber 2585 cm^-1 has zero intensity which explains the bend is IR inactive with no change in the dipole moment, therefore no peak detected at this wavenumber. From the table above, it is obvious that there are two pairs of degenerate vibrations, one from bend at 1213 cm^-1 and the other from stretch at 2716 cm^-1. The degeneracy gives the same energy for the two equivalent peaks and they overlap to show as a single signal. Therefore, 3 active peaks at wavenumber 1163 cm^-1 with medium intensity, at 1213 cm^-1 with small intensity and at 2716 cm^-1 with the largest intensity are shown in the IR spectrum.

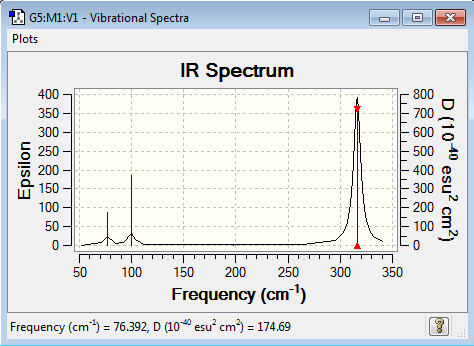
GaBr₃:B3LYP/6-31G(d,p)

Frequency file: DOI:10042/193837

summary data	low modes
	Low frequencies --- -1.4878 -0.0015 -0.0002 0.0096 0.6540 0.6540 Low frequencies --- 76.3920 76.3924 99.6767

Vibrational spectrum for GaBr₃

Wavenumber	Intensity	IR active?	Type
76	3	very slight	bend
76	3	very slight	bend
100	9	very slight	bend
197	0	no	stretch
316	57	yes	stretch
316	57	yes	stretch

|

Same as BH₃, the IR spectrum of GaBr₃ only gives 3 vibrational peaks. The bending at wavenumber 197 cm^-1 doesn't involve any change in the dipole moment, so it is IR inactive with zero intensity and is absent from the IR spectrum. Also, there are two sets of equivalent vibrational modes at wavenumber 76 (bending) and 316 (stretching) cm^-1. In each case, two exactly same peaks overlap to appear as a singlet peak with doubled intensity. In brief, the 3 peaks at wavenumber 76 cm^-1 with very slight intensity, at 100 cm^-1 with small intensity and at 316 cm^-1 with large intensity are shown clearly in the IR spectrum.

Discussion of the large difference in the value of the frequencies for BH₃ compared to GaBr₃

Used equation of wavenumber: 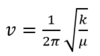(Copy of the reconstruction in the word file)

GaBr₃ generally has much smaller order of vibrational frequencies than BH₃. Firstly, Ga and Br are greatly heavier than B-H in atomic masses. According to the equation related wavenumber to reduced mass (shown above), a larger reduced mass would result a smaller frequencies in vibration. The comparison of frequencies well matched the previous discussion of Ga-Br (2.35 Å) and B-H (1.19 Å) bond lengths, as well. Ga-Br bond is almost twice longer than B-H and its weakness requires much smaller energy input to bend or stretch the GaBr₃ molecules than BH₃. Ga is further down than B in the same group, so the more diffused valence orbital of Ga would decrease the positive attraction from the nucleus. Br is much larger and electronegative than H. The relatively small B and H atoms could bond tightly with better orbital overlap than Ga and Br whose valence orbitals are much larger and diffused. And due to the electronegative character of Br, it prefers to capture the electrons from Ga over sharing electrons. Therefore, the Ga-Br bond is weaker than B-H and has lower values of bending and stretching frequencies.

Compare the relative frequency and intensity of the umbrella motion for the two molecules

GaBr₃ and BH₃ have same types of vibrational motions when the input energy is provided, out-of-plane bending (umbrella and twisted scissoring) and in-plane stretching. The umbrella bending motions of GaBr₃ and BH₃ occur at 100 cm^-1 and 1163 cm^-1 respectively. From the Gaussview, GaBr₃ has only one leading displacement vector along the motion direction of central Ga atom and the three Br ligand atoms almost fix in their positions with little displacements. This is because Ga is lighter in mass than Br atom and less energy is required to make the Ga atom vibrate. It can conclude that the umbrella motion of GaBr₃ is prefered to be dominated by Ga atom.

In contrast, BH₃ has opposite motion situation where the central B atom almost doesn't move and the outside H atoms undergo the umbrella bending, proving by the obvious displacement vectors in each H. In BH₃, the umbrella motion is dominated by H as H is lighter than B. Since the vibrational frequency is inversely proportional to the reduced mass of molecule, the heavy Ga and Br atoms give GaBr₃ a smaller bending frequency than BH₃ and therefore low vibrational energy. It means the umbrella bending is less favourable in GaBr₃.

Importance of optimisation and frequency analysis calculations

Different functions in basis set are computed to give the potential energy surface (PES) of a molecular system, in order to well describe its electronic structure later. The optimisation of a molecule determines first derivatives i.e. the stationary points in the PES but without distinguishing them futher. At that stage, whether the geometry at zero gradient is a transition or ground state is not known. In order to find out if the stationary points are minima or maxima, second derivative calculation is introduced under frequency analysis. When using the same computation method and basis set, optimisation and frequency analysis are consistent in the calculation and their results can be directly related and compared. The second derivatives are straightforward determined from the frequency analysis. By having all positive frequencies, we could ensure the existence of a minimum i.e. a ground state. The occurrences of negative values show the molecular system has a stationary point as a maximum i.e. a transition state or not a local extremum, which indicates the failure of optimisation.

The 'Low frequencies' represent the 6 frequencies that needs to be eliminated when calculating the number of vibrational frequencies through the equation 3N-6 for a non-linear molecule. When the molecule undergoes vibrations in 3D space, translational and rotational degrees of freedom moving around the 3 Cartesian axes generate no change in their nuclear coordinates. Here, we are talking about Al₂Cl₄Br₂, any change in the atomic centres of mass could be neglected compared to their heavy nuclei. It explains the first-line frequencies are much smaller than the second-line vibration frequencies, as well. The Born-Oppenheimer Approximation states as the nuclear is much heavier in mass, the nuclear could be assumed to be fixed in position relative to the fast electronic motion. Therefore, the closer the 6 first-line frequencies compared to zero, the better quantum mechanics calculation has been done by the computation method.

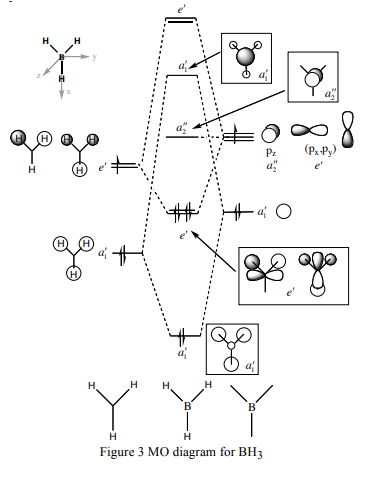
Molecular Orbitals diagram of BH₃

Population analysis DSpace DOI:10042/193839

Compare with qualitative MO theory

From the above MO diagram of BH₃, the real molecular orbitals show clearly the feature of diffused orbitals in desired shapes and geometries, while the LACO MOs only show the simple combination of atomic orbitals with no further modification of their arrangements. In general, the LCAO MOs model the real molecular orbitals quite well with no significant differences. It means the theoretical MO theory is accurate enough to give a valid prediction of molecular orbitals for the molecules with smaller or similar size of BH₃. But the application of computational method is suggested to give a view of more realistic MOs, especially the change in the lobe shape.

NH₃:B3LYP/6-31G(d,p) level

Optimisation log file here

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000012 0.001800 YES RMS Displacement 0.000008 0.001200 YES	optimised ammonia molecule

Frequency file: here

summary data	low modes
	Low frequencies --- -0.0130 -0.0028 -0.0002 7.0722 8.1014 8.1017 Low frequencies --- 1089.3849 1693.9369 1693.9369

Vibrational spectrum for NH₃

Wavenumber (cm-1)	Intensity	IR active?	Type
1089	145	yes	bend
1694	14	slight	bend
1694	14	slight	bend
3461	1	no	stretch
3590	0	no	stretch
3590	0	no	stretch

NBO analysis of NH₃

Population analysis log file here

Summary of Natural Population Analysis:                  
                                                         
                                      Natural Population 
               Natural  -----------------------------------------------
   Atom  No    Charge         Core      Valence    Rydberg      Total
-----------------------------------------------------------------------
     N    1   -1.12514      1.99982     6.11104    0.01429     8.12514
     H    2    0.37505      0.00000     0.62250    0.00246     0.62495
     H    3    0.37505      0.00000     0.62250    0.00246     0.62495
     H    4    0.37505      0.00000     0.62250    0.00246     0.62495
=======================================================================
  * Total *    0.00000      1.99982     7.97852    0.02166    10.00000

Atom N and H has respective charge distributions -1.125 and 0.375.

Day 4 Association Energy of NH₃BH₃

NH₃BH₃:B3LYP/6-31G(d,p) level

Optimisation log file here

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000016 0.000060 YES RMS Displacement 0.000007 0.000040 YES	optimised NHBH molecule

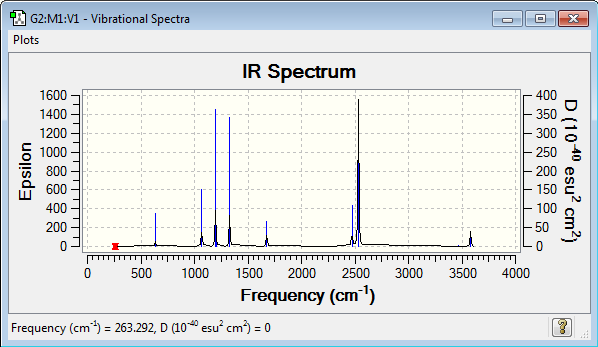
NH₃BH₃ frequency analysis: B3LYP/6-31G(d,p)

Frequency analysis log file here

summary data	low modes
	Low frequencies --- -5.5821 -0.2698 -0.0388 0.0008 1.3925 1.4497 Low frequencies --- 263.2918 632.9559 638.4632

Vibrational spectrum for NH₃BH₃

Wavenumber (cm-1)	Intensity	IR active?	Type
263	0	no	bend
633	14	slight	strecth
638	4	very slight	bend
638	4	very slight	bend
1069	41	yes	bend
1069	41	yes	bend
1196	109	yes	bend
1204	3	very slight	bend
1204	3	very slight	bend
1329	114	yes	bend
1676	28	slight	bend
1676	28	slight	bend
2472	67	yes	stretch
2532	231	yes	stretch
2532	231	yes	stretch
3464	3	very slight	stretch
3581	28	slight	stretch
3581	28	slight	stretch

Dissociation Energy of the NH₃BH₃ bond

E(NH₃)=-56.5577687 a.u.

E(BH₃)=-26.6153236 a.u.

E(NH₃BH₃)=-83.2246891 a.u.

ΔE=E(NH₃BH₃)-[E(NH₃)+E(BH₃)]=-0.0515968 a.u.=-135.47 kJ/mol

When applying the same calculation procedure to NH₃BH₃, there are several low frequencies that exceed the allowed range of plus/minus 15cm^-1 which indicates considerable errors in the frequency analysis of NH₃BH₃. After discussing with the demonstrator, a tight convergence criteria was applied in calculating the energy of ammonia-borane and the results obtained are within the allowed range which are satisfied. In order to meet the high accuracy, the energies of NH₃ and BH₃ should undergo the same settings, as well. But almost exactly same energies were obtained with and without the tight constrain in calculation. According to Dr. Hunt's suggestion, the energies shown above for NH₃ and BH₃ are still without further modification in the constrain since they are already good enough to go to next step's calculation at this level.

Comment on the dissociation energy

B and N are in the same period and well matched in atomic size. N is quite electron-withdrawing so the big electronegativity difference contributes some ionic character to the B-N bond which decreases their valence orbital overlap. Regarding to the N-N bond energy of 170 kJ/mol in the previous discussion of bond strength, the association of NH₃ and BH₃ involves medium-sized energy, 135 kJ/mol to form the B-N bond.The B-N bond is much smaller than the strong covalent or ionic bond energy value but larger than the weak intermolecular attractions.

Project: Lewis Acids and Bases

There are 6 isomers for Al₂Cl₄Br₂ molecule with Br atoms in bridging or terminal positions. Isomer 5 and 6 are superimposable mirror images which are a pair of enantiomers with approximately same energy and it is difficult to distinguish them. For the following analysis, only isomers 1 to 5 will be discussed and isomer 6 is seen to be equivalent to isomer 5.

6 isomers of Al₂Cl₄Br₂

The optimisation of Al₂Cl₄Br₂ will be separated according to atoms. Al and Cl will use a high level basis set, GEN/6-31G(d,p). As mentioned in the computational lab script, Br has 35 electrons which cannot apply well to the standard Schrodinger equation due to the relativistic effect, but instead the pseudo-potentials could accurately modify the core electrons in a heavy atom, especially for the elements in the third row. As a result, an improved basis set PP LANL2DZ is going to be set on Br. When doing the optimisation for Al₂Cl₄Br₂, the 'Additional key words' must contain 'pseudo=read gfinput integral=grid=ultrafine' to ensure the core electrons in Br will be included in the desired calculation. A tight convergence criteria is also consistently applied to improve the optimisation.

Introduction of dimer Al₂X₆

AlX₃ (X represents a halogen atom) is an unstable monomer with 6 valence electrons and it starts to dimerise in order to relieve the electron deficiency and increase the stability in the electronic configuration of its outer shell. In Al₂X₆, the terminal Al-X bond is a sigma interaction formed by sharing two electrons between two atoms and this chemical bond is considered to be electron rich. While the bridging halogen connects to two Al atoms at the same time which forms a relatively electron deficient Al-X-Al bond as 2 electrons are shared among 3 centres. The Al-X-Al bridge is suggested to be formed by one p orbital of the halogen interacting with two sp³ Al orbitals. Alternatively, the two X₂Al and two X fragments provide 4 electrons in total for bonding, therefore each Al-X-Al bridge contains 2 electrons only. The 2 electrons located in the bonding molecular orbitals are now spread out across the 3 atomic centres. One of the Al-X interactions in the bridging is represented as a covalently dative bond through the donation of electron density from halogen to Al such that the AlX₃ accepting the donation is a Lewis acid and the other donor is a Lewis base. Also, the 3c-2e bridging interaction is longer than the localised 2c-2e terminal bond which signifies the increased bond order of the terminal Al-Br bond. It corresponds to the trend that Al-Br terminal stretchings generally have much larger frequencies than bridging since more energy input is in need to vibrate terminal Al-Br bond (See later discussion).

In addition, a similar molecule Al₂Me₆ suggests a short distance between 2 Al centres in terms of direct Al-Al interaction. Although the halogen atoms are much larger in size than C, the bond angle in the Al-X-Al bridge should be larger which it potentially reduces the probability that two Al orbitals get into touch. But it is still expected to have some degree of Al-Al interaction in the dimeric aluminium-halogen molecules. However, this is not the part of the main content of this computational lab and more information is in need to explore further on this topic.

Al₂Cl₄Br₂: Isomer 1

Isomer 1: Point Group C1

Optimisation DSpace DOI:10042/193889

Optimisation log file here

Summary data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000007 0.000060 YES RMS Displacement 0.000003 0.000040 YES	optimised Al2Cl4Br2 molecule

Isomer 1: Point Group C_2v

Optimisation DSpace DOI:10042/193865

Optimisation log file here

Summary data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000015 0.000060 YES RMS Displacement 0.000005 0.000040 YES	optimised Al2Cl4Br2 molecule

The constructed Al₂Cl₄Br₂ isomer 1 undergoes the Gaussian calculation on optimisation before imposing the symmetry. And after assigning C_2v as point group for isomer 1, the molecule was optimised again. The energies for the two point groups C1 and C_2v of optimised isomer 1 are found to be exactly same as shown above. Therefore, the rest 5 isomers were directly imposed the corresponding point group without breaking their symmetries and then applied to the Gaussian calculation on optimisation. With the advice from Dr. Hunt, there is no need to repeat the simulation and calculation for other C1 isomers as we already know they would give the same energy values as their point groups.

Al₂Cl₄Br₂ frequency analysis: GEN/6-31G(d,p) level on Al and Cl, PP LANL2DZ on Br

Frequency DSpace DOI:10042/193866

Frequency analysis log file here

Summary data	Low modes
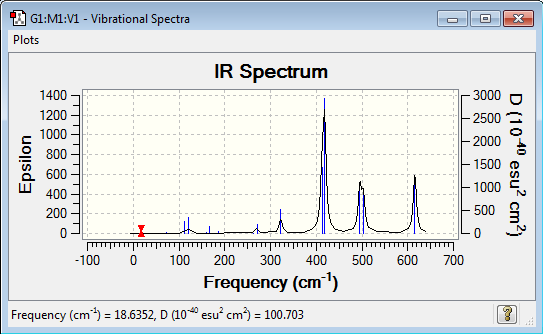
	Low frequencies --- -0.7382 -0.5588 -0.0024 0.0005 0.0018 2.0861 Low frequencies --- 18.6352 51.2122 72.2018

Vibrational spectrum for Al₂Cl₄Br₂

Wavenumber (cm-1)	Intensity	IR active?	Type
19	0	no	bend
51	0	no	bend
72	1	very slight	stretch
98	0	no	stretch
112	0	no	bend
112	7.5	very slight	bend
120	11	very slight	stretch
160	3	very slight	stretch
166	7	very slight	bend
187	2	very slight	stretch
263	0	no	stretch
271	14	very slight	stretch
323	41	very slight	stretch
413	150	yes	stretch
418	309	yes	stretch
495	134	yes	bend
503	105	yes	stretch
616	177	yes	bend

Al₂Cl₄Br₂: Isomer 2

Optimisation DSpace DOI:10042/193867

Optimisation log file here

Summary data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000025 0.000060 YES RMS Displacement 0.000011 0.000040 YES	optimised Al2Cl4Br2 molecule

Al₂Cl₄Br₂ frequency analysis: GEN/6-31G(d,p) level on Al and Cl, PP LANL2DZ on Br

Frequency DSpace DOI:10042/193868

Frequency analysis log file here

Summary data	Low modes
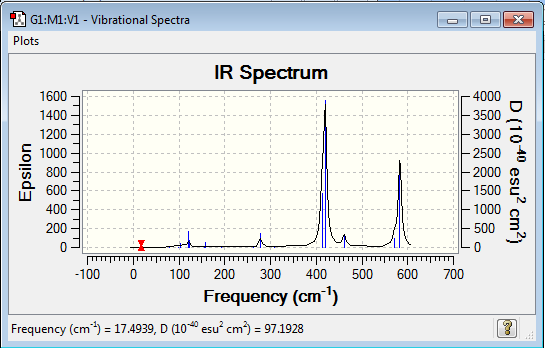
	Low frequencies --- -1.3471 -0.7287 -0.0035 -0.0034 -0.0033 2.1924 Low frequencies --- 17.4939 51.1433 78.5269

Vibrational spectrum for Al₂Cl₄Br₂

Wavenumber (cm-1)	Intensity	IR active?	Type
18	0	no	bend
51	0	no	bend
79	0	no	bend
99	0	no	bend
103	3	very slight	bend
121	13	very slight	bend
123	6	very slight	bend
157	0	no	stretch
158	5	very slight	bend
194	2	very slight	bend
263	0	no	stretch
279	26	very slight	stretch
308	3	very slight	bend(?)
413	150	yes	stretch
420	410	yes	bend
461	35	very slight	bend
571	33	very slight	bend
583	277	yes	bend

Al₂Cl₄Br₂: Isomer 3

Optimisation DSpace DOI:10042/193869

Optimisation log file here

Summary data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000003 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000025 0.000060 YES RMS Displacement 0.000008 0.000040 YES	optimised Al2Cl4Br2 molecule

Al₂Cl₄Br₂ frequency analysis: GEN/6-31G(d,p) level on Al and Cl, PP LANL2DZ on Br

Frequency DSpace DOI:10042/193870

Frequency analysis log file here

Summary data	Low modes
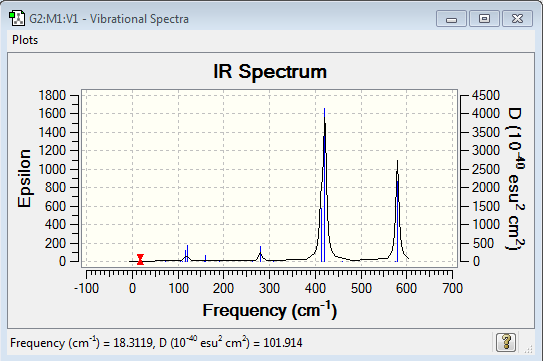
	Low frequencies --- -0.7108 -0.5839 0.0010 0.0024 0.0032 2.2204 Low frequencies --- 18.3119 49.2151 72.9030

Vibrational spectrum for Al₂Cl₄Br₂

Wavenumber (cm-1)	Intensity	IR active?	Type
18	0	no	bend
50	0	no	bend
79	0	no	bend
105	0	no	bend
109	0	no	bend
117	9	very slight	bend
120	13	very slight	bend
157	0	no	stretch
159	6	very slight	bend
192	0	no	bend
263	0	no	stretch
280	29	very slight	stretch
307	0	no	stretch
413	149	yes	stretch
421	438	yes	bend
459	0	no	bend
575	0	no	bend
580	316	yes	bend

Al₂Cl₄Br₂: Isomer 4

Optimisation DSpace DOI:10042/193872

Optimisation log file here

Summary data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000003 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000054 0.000060 YES RMS Displacement 0.000015 0.000040 YES	optimised Al2Cl4Br2 molecule

Al₂Cl₄Br₂ frequency analysis: GEN/6-31G(d,p) level on Al and Cl, PP LANL2DZ on Br

Frequency DSpace DOI:10042/193873

Frequency analysis log file here

Summary data	Low modes
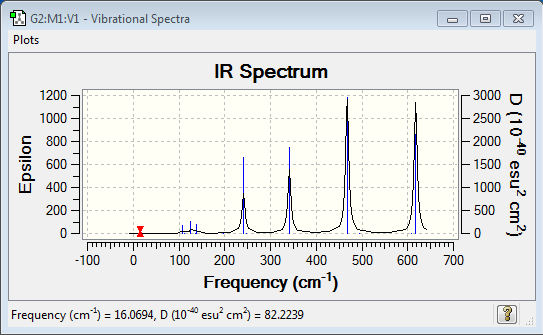
	Low frequencies --- -0.7247 0.0032 0.0048 0.0050 1.2793 1.4266 Low frequencies --- 16.0694 63.6230 86.1138

Vibrational spectrum for Al₂Cl₄Br₂

Wavenumber (cm-1)	Intensity	IR active?	Type
17	0	no	bend
64	0	no	bend
86	0	no	bend
87	0	no	bend
109	5	very slight	bend
111	0	no	bend
126	8	very slight	bend
135	0	no	bend
138	7	very slight	bend
163	0	no	stretch
197	0	no	stretch
241	100	yes	stretch
247	0	no	stretch
341	161	yes	stretch
468	346	yes	stretch
494	0	no	stretch
609	0	no	bend
617	332	yes	bend

Al₂Cl₄Br₂: Isomer 5

Optimisation DSpace DOI:10042/193874

Optimisation log file here

Summary data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000008 0.000015 YES RMS Force 0.000003 0.000010 YES Maximum Displacement 0.000024 0.000060 YES RMS Displacement 0.000009 0.000040 YES	optimised Al2Cl4Br2 molecule

Al₂Cl₄Br₂ frequency analysis: GEN/6-31G(d,p) level on Al and Cl, PP LANL2DZ on Br

Frequency DSpace DOI:10042/193875

Frequency analysis log file here

Summary data	Low modes
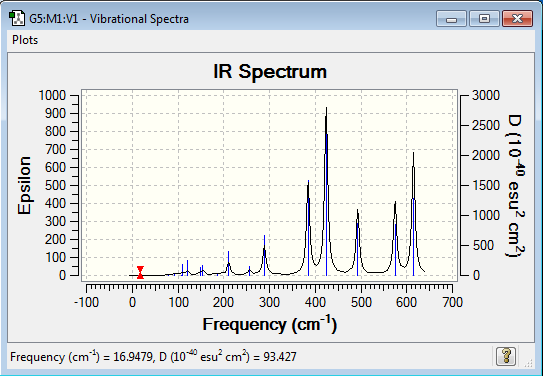
	Low frequencies --- -0.1011 -0.0022 -0.0017 -0.0008 1.1172 1.8133 Low frequencies --- 16.9479 55.9203 80.0644

Vibrational spectrum for Al₂Cl₄Br₂

Wavenumber (cm-1)	Intensity	IR active?	Type
17	0	no	bend
56	0	no	bend
80	0	no	bend
92	1	very slight	bend
107	0	no	bend
110	5	very slight	bend
121	8	very slight	bend
149	5	very slight	bend
154	6	very slight	bend
186	1	very slight	stretch
211	21	very slight	stretch
257	10	very slight	stretch
289	48	very slight	stretch
384	153	yes	stretch
424	275	yes	bend
493	107	yes	stretch
576	122	yes	bend
615	197	yes	bend

Al₂Cl₄Br₂: Isomer 6

Optimisation DSpace DOI:10042/ch/189641

Optimisation log file here

Summary data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000008 0.000015 YES RMS Force 0.000003 0.000010 YES Maximum Displacement 0.000026 0.000060 YES RMS Displacement 0.000009 0.000040 YES	optimised Al2Cl4Br2 molecule

Al₂Cl₄Br₂ frequency analysis: GEN/6-31G(d,p) level on Al and Cl, PP LANL2DZ on Br

Frequency DSpace DOI:10042/193877

Frequency analysis log file here

Summary data	Low modes
	Low frequencies --- -0.0867 0.0024 0.0030 0.0036 1.1185 1.8139 Low frequencies --- 16.9479 55.9203 80.0644

Vibrational spectrum for Al₂Cl₄Br₂

Wavenumber (cm-1)	Intensity	IR active?	Type
17	0	no	bend
56	0	no	bend
80	0	no	bend
92	1	very slight	bend
107	0	no	bend
110	5	very slight	bend
121	8	very slight	bend
149	5	very slight	bend
154	6	very slight	bend
186	1	very slight	stretch
211	21	very slight	stretch
257	10	very slight	stretch
289	48	very slight	stretch
384	153	yes	stretch
424	275	yes	bend
493	107	yes	stretch
576	122	yes	bend
615	197	yes	bend

Comparison of the 5 isomers of Al₂Cl₄Br₂

6 isomers of Al₂Cl₄Br₂

Comparison of IR Spectra

Isomer	Point Group	IR Spectra	No. of bands	No. of remarkable peaks in IR spectra
Isomer 1	C2v		13	3
Isomer 2	C2v		12	2
Isomer 3	C2h		7	2
Isomer 4	D2h		7	4
Isomer 5	C1		14	6

Discussion on IR bands

All isomers show sharp peaks and share some similarities in their IR spectra. The number of bands in the table above counts the bands with non-zero intensity in the 'Frequency analysis', and the number of remarkable peaks in the IR spectra ignores those bands with low intensities. During the following discussion, the last two column data will be both referred to.

The necessary criteria for a vibrational mode to be IR active is a net change in dipole moment of the molecule. It could be achieved by changing the charge difference or the distance between two charges. The lower the symmetry a molecule has, a larger number of bands would appear in the IR spectra. Isomer 5 has a point group C1, the lowest symmetry among the 5 isomers and it inherently owns no symmetrical features such as axis or plane of symmetry. When the asymmetrical isomer 5 undergoes vibrations or rotations involving any small fluctuations in the positions of constituted atoms, there must be an expected change in dipole moment giving IR active bands. So it is reasonable to suggest isomer 5 to have the largest number of bands in IR spectra which corresponds to the data in the table above.

On the other hand, isomer 4 is highly symmetrical with D_2h as point group. It has 3C₂ along the Cartesian axes as well as three horizontal reflection planes. The number of bands in isomer 4 is far less than isomer 5 because when symmetrical stretching take place in isomer 4, the changes in dipole moments of two sides could cancel to each other giving on net change in magnitude of charge or the charge separation.

Isomer 1 and 2 share the common point group C_2v and they do have almost same number of IR active vibrational modes. Isomer 3 has a same level of symmetry to 1 and 2, but it experiences the fewer IR active bands. However, its IR spectra is highly analogue to isomer 2's.

Comparison of Energy

Isomer	Isomer 1	Isomer 2	Isomer 3	Isomer 4	Isomer 5	Isomer 6
Energy/ a.u.	-2352.41634373	-2352.41627846	-2352.41630099	-2352.40632551	-2352.41110734	-2352.41110734
Relative energy / kJ/mol	the lowest energy conformer	0.17	0.11	26.30	13.75	13.75

Isomer 1 is the conformer with the most negative energy value, so it is concluded that having two Br atoms in terminal positions would be the most stable geometry for Al₂Cl₄Br₂. The stabilities of isomers 2 and 3 are comparable to 1, simply with little energy difference (less than 0.20 kJ/mol) and they could still be considered as stable conformers. Isomer 5 and 6 has medium stabilities, and also it proves that these two enantiomers do have exactly same energy values. The largest relative energy shows when involving two Al-Br-Al bridges, Al₂Cl₄Br₂ would be very unstable, therefore it is unfavoured to have isomer 4 in this case. It may be because the weaker Al-Br bond nature recedes the bridge strength.

Optimisation on AlCl₂Br monomer

Optimisation DSpace DOI:10042/ch/189655

Optimisation log file here

Exactly same settings for Al₂Cl₄Br₂ are applied to the optimisation calculation on the monomer AlCl₂Br.

Summary data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000000 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000000 0.000060 YES RMS Displacement 0.000000 0.000040 YES	optimised AlCl2Br molecule

Dissociation Energies of Al₂Cl₄Br₂ bond

E(AlCl₂Br) = -1176.19014036 a.u.

E(Al₂Cl₄Br₂) = -2352.41634373 a.u.

ΔE = E(Al₂Cl₄Br₂) - 2E(AlCl₂Br)=-0.03606301 a.u. = -94.68 kJ/mol

The calculation concludes that the dimer arrangement of AlCl₂Br is more stable than the isolated monomer as the energy of dimer is larger than the total energy of 2 monomers. The element Al has 3 valence electrons and forms 3 covalent bonds with 2 Cl and 1 Br atoms by using Al's 2s and two of the 2p orbitals to give 3 hybridised sp² orbitals. In the monomer, Al has 6 valence electrons and it is still electron deficient, acting as a Lewis acid. In order to achieve the Lewis octet i.e. 8 electrons in the outer shell, a halogen ligand from a neighbouring molecule (the Lewis base) forms an additional dative bond with the Al center through the donation of a lone pair of electron into the empty p orbital of Al. Therefore, it generates the dimer form. The 2 Cl atoms act as bridges in a 3c-2e bond connecting 2 Al. Now we could suggest the Al to be sp³ hybridised as the 4 Cl ligands are tetrahedrally arranged.

In this project we actually have AlCl₂Br as the monomer, but here we could use AlCl₃ for the comparison with BCl₃ which prefers the trigonal planar geometry as a monomer. The element B is in the same group as Al, so they would have the same electronic features. But B is smaller than Al and it differs more in atomic size to Cl. In the form of dimer, the central B atom may not have enough space to occupy 4 halogen ligands. Instead of that, BCl₃ is stabilised by the donation of the lone pairs of electrons from the halogen ligands to the empty p orbital in B which forms a conjugation system. In the contrast, B₂H₆ is usually a dimer because the H atom is small which gives space for the bridging.

Discussion on Al-Br stretching vibrations in terms of terminal Br

Although the displacement vectors are missing for some atoms, all atoms are actually involved in the vibrational modes. When enlarging the vibrations in scale, it is obvious that the Br atoms always has a shorter displacement vector than Al and Cl. It is attributed to the heavy mass of Br which makes it vibrate less than Al and Cl under the same stretching energy.

Comparison of Al-Br stretching vibrations with terminal Br

Isomer	Point Group	Stretching Image	No. of Mode	Frequency	Intensity
Isomer 1	C2v		16	495	134
Isomer 2	C2v		18	583	277
Isomer 3	C2h		18	580	316
Isomer 4	D2h		18	617	332
Isomer 5	C1		17	575	122

Order of increasing frequency: isomer 1, 5, 3, 2 and 4

Order of increasing intensity: isomer 5, 1, 2, 3 and 4

Here we are looking at the terminal Al-Br stretching vibrations. Isomer 4 has no terminal Br atoms as they 'bridge' the two Al centres, but terminal Al-Cl stretching is going to be observed instead. There is only one terminal Al-Br stretching vibration in isomers 1 and 5, while isomers 2, 3 and 4 have doubly degenerate vibrational motions which involves both Al atoms. The terminal environments of Al centres are same in each of the isomers 2, 3 and 4. For example, each Al centre in isomer 3 bonds to one terminal Br and one terminal Cl atom. The 'symmetric' features in isomers 2, 3 and 4 make their two Al atoms undergo the terminal stretching at the same time, and this explains why their vibration intensities are doubled in magnitude compared to the values for isomers 1 and 5. Isomer 4 has the largest frequency and intensity and it is suggested to have the most effective stretching in this vibrational mode.

In isomers 1 and 5, there is also an equivalent terminal stretching for the other Al centre connecting two terminal Cl atoms, but the modes are not shown here. In both isomers 1 and 5, terminal Al-Cl stretching has a larger frequency than Al-Br vibration. In the periodic table, Al and Cl are in the same period and they are better matched in atomic size than Al and Br. The larger orbital overlap and high electronegativity of Cl offer a shorter and stronger Al-Cl bond which requires more energy to be vibrationally stretched.

Discussion on Al-Br stretching vibrations in terms of bridging Br

Comparison of Al-Br stretching vibrations with bridging Br

Isomer	Point Group	Stretching Image	No. of Mode	Frequency	Intensity
Isomer 1	C2v		12	271	14
Isomer 2	C2v		12	279	26
Isomer 3	C2h		12	280	29
Isomer 4	D2h		13	247	0
Isomer 5	C1		12	257	10

Order of increasing frequency: isomer 4, 5, 1, 2 and 3

Order of increasing intensity: isomer 4, 5, 1, 2 and 3

From the table above, only isomers 4 and 5 involve Br as bridging atoms in the structure, but the Al-Cl-Al bridging will still be considered to discuss the effect of substituting bridging Cl by Br. The stretching images chosen all show highly similar vibrational motions of bridging atoms and some may also involve the considerably large movements of the terminal ligands.

As mentioned before, a high stretching frequency corresponds to a rigid bond which needs a great amount of energy to disturb it. Isomers 4 and 5 have the lowest bridging-stretching frequencies which comes from the weaker Al-Br-Al bridge than Al-Cl-Al. Again, the high electronegativity and well-matched orbital size of Cl urges it to bond strongly with Al. Therefore, isomer 4 has an even lower frequency than 5. Another important thing is the intensity for isomer at 247cm^-1 is zero. We can see from its image, isomer 4 is stretched towards two sides and its high symmetry makes the changes in dipole moments on the left and right hand sides compensate, resulting in no net change in dipole moment. This explains why this vibrational mode is IR inactive and not shown in the IR spectra.The isomers 2 and 3 with Cl as bridging atoms share an approximately same stretching frequency around 280 cm^-1 because they have highly similar molecular environments where each Al centre bonds to one terminal Cl and one terminal Br. Isomer 1 experiences a bit lower frequency than 2 and 3. Here the two bridging Cl atoms vibrate away from the terminal Br atoms. It is suggested that the vibrated motion of terminal Br needs to be balanced by the bridging atoms moving in the opposite direction. Also, it is suggested from the results that locating two terminal Br atoms on one side could decrease the frequency required for the stretch in isomer 1. But the main reason in the frequency difference between 1 and 2 or 3 is the change in the molecular environment which could not be quantitatively discussed at this stage.

MO analysis on Isomer 1

Under MO constructions in Gaussview, 54 numbered occupied molecular orbitals are given from low to high energy. We only need to concentrate on the MOs starting from the number 31 as the first 30 MOs from the lowest energy show the localised molecular orbitals in certain atoms with few characteristics of delocalisation. The 37th, 40th, 43rd, 46th, and 48th MOs are chosen for further bonding analysis due to their interesting features in the orbital shape or arrangement. During the following interpretations, the 3D shape, top view and side view will be presented. The theoretical MO diagram for each MO analysis is also reconstructed for comparison.

Each MO contains a number of bonding or antibonding interactions and part of them are highly similar. In the diagrams below, the typical orbital interactions are annotated using arrows and in the redrawn MO diagram, the elements are ignored leaving main orbitals and only important bonding characters will be given as arrows.

The bonding and antibonding interaction can be classified as:

1. Weak, medium and strong in terms of strength;

2. Strong directional overlap and weak through space interaction (There will be some very weak through space interactions between atoms which can be neglected as the atoms are too far away from each other.);

3. s-p overlap and head-to-head p-p overlap as sigma bonds, and side-by-side p-p overlap as pi system where pi bonds are always stronger than sigma and s-p overlap is stronger than p-p sigma interaction.

Another important thing in the orbital diagrams is the node or nodal plane i.e. a region with no electron density. A nodal plane appears when there are at least two nodes in the same plane. The intranuclear node is a characteristic point in the middle of the p orbital but it is much less important than the node in the any internuclear region.

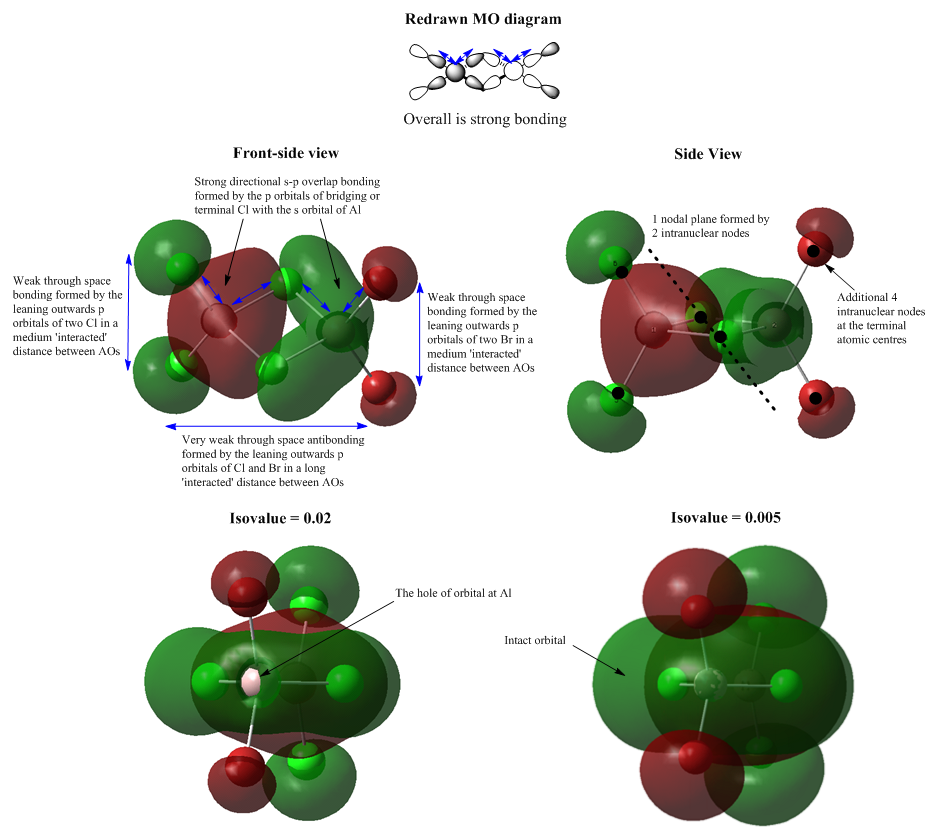
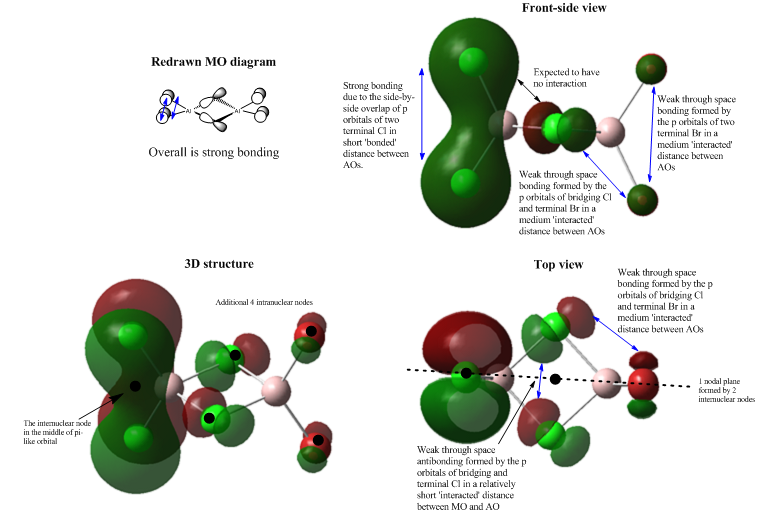
Molecular Orbital 37

MO 37 is a strongly bonding interaction. The s orbital of each Al centre overlaps with the p orbital of each tetrahedrally bonded Cl in the right symmetry. 3 bonding interactions work together and this spreads out the red lobe in the middle over the 4 Al-Cl bonds. Same interaction is viewed in the opposite side. But the green lobe seems to be more diffused than the red one. Also, when view MO 37 from the right hand side, there is a hole at the position of Al in the big green lobe. After discussed with Dr. Hunt, I changed the 'Isovalue' from 0.02 to 0.005 in the settings and finally got a new MO 37 with intact orbitals. This doesn't apply any change to the MO itself, but just 'cut' the orbital shell in a different way which is controlled by the 'Isovalue'. The middle MO i.e. the big red and green lobe region lies along the bridging bonds which means it is entirely a sigma interaction. Again, the central delocalised bonding character dominates this MO 37 and gives an overall strong bonding.

Each bridging Cl atom has a less important intranuclear node which contributes to the formation of a nodal plane. There is also an intranuclear node locating at the centre of terminal atom which reflects the instinct feature of the phase change in the p orbital.

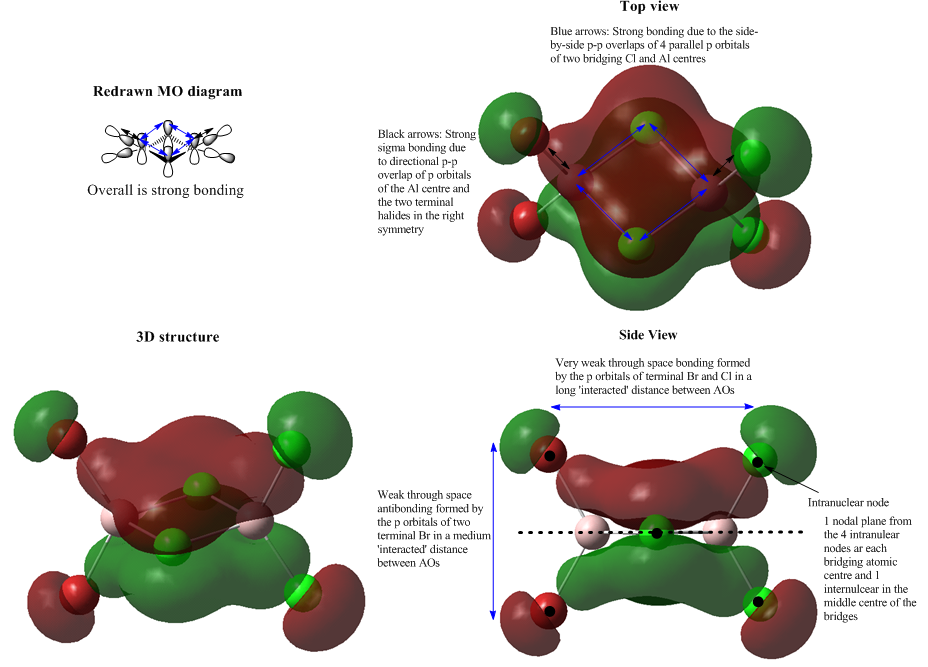
Molecular Orbital 40

MO 40 is a special interaction as it reveals an aromatic-analogue character in the molecule. The bridging Al and Cl atoms generate a strong bonding cluster under the overlap of 4 p orbitals. Each Al interacts with its terminal halogens at the same time. The generated MOs are close in distance and they delocalise to form two flat lobes, the central red and green region. From the side view of MO 40, the lobe cluster is perpendicular to the plane of the 4 bridging atoms which indicates a pi framework in this central MO. It is not expected to see in the redrawn MO diagram, but the computed MO shows a more real situation of the interaction between atomic orbitals. This pi cluster supports the stability of the MO as it dominates the bonding character and the very weak through space antibonding is not comparable. Therefore, MO 40 is overall strong bonding and highly delocalised in the middle region.

There are 4 intranuclear nodes at terminal positions, as well as 4 intranuclear nodes at bridging atoms and an internuclear node in the middle of the plane of the bridges which gives a perfect nodal plane.

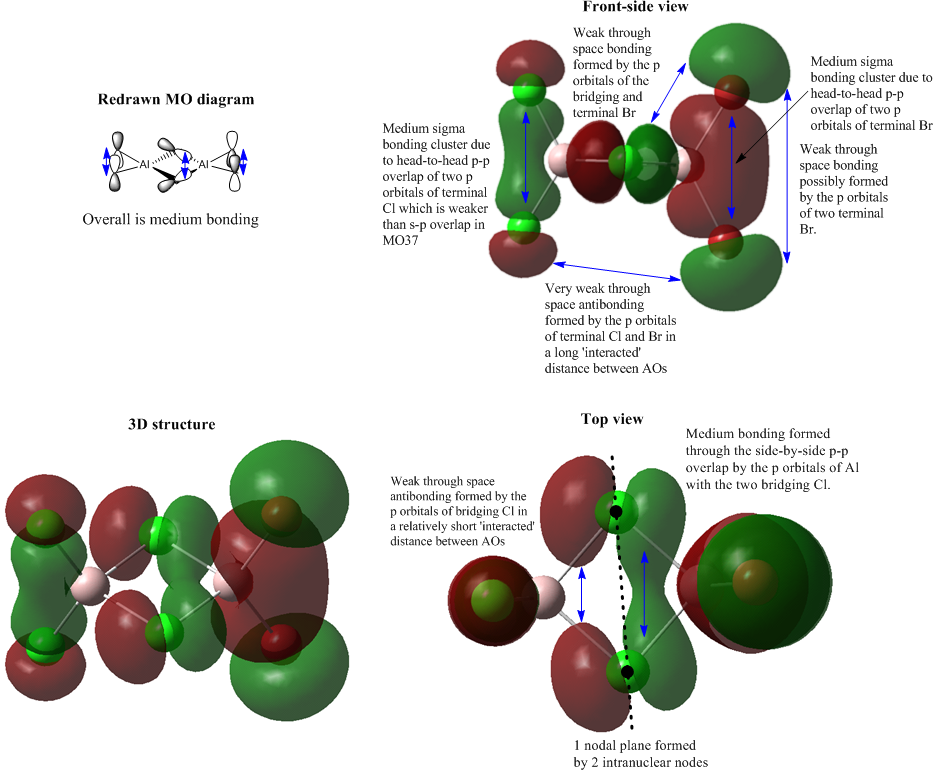
Molecular Orbital 43

The main bondings in MO 43 are the two sigma bonding between the p orbitals of terminal ligands. From the redrawn MO diagram, it is clear that the two p orbitals from each pair of terminal halides are head-to-head and aligned to each other which maximises their overlap. But this p-p overlap is weaker than the s-p overlap which is involved in the MO 37. From the top view of MO 43, it is important that there is a direct bonding character between two bridging Cl atoms which hasn't been shown in the redrawn MO diagram. This p-p overlap exhibits the real electronic interaction between the bridging bonds. The central MO is orthogonal to the MOs on two sides. As orthogonal orbitals don't interact, it reduces the potential antibonding between these MOs. As the annotation in the diagram, MO 43 mainly experience direct bonding with few weak through space antibonding, and overall it is medium bonding. The central MO is delocalised between two bridging Cl atoms. The left-hand-side green lobe is more condensed than the left red one. Also, the left green lobe has a smaller orbital size than the right red one which means the red lobe contributes more to the overall MO 37.

It only has a nodal plane comprised by two intranulear nodes at bridging Cl atoms.

Molecular Orbital 46

All aomic orbitals in this MO are distant, so they are relatively weakly interacted. The p orbitals of terminal Br are leaning outwards while the rest p orbitals of Cl are vertically parallel to each other which favours their interaction in the correct symmetry. From the top view, only the p orbitals of two bridging Cl are in phase and they are weakly bonded. The other orbitals all form weak through space antibondings, leading the overall MO 46 to be weaklt antibonding. Only atomic orbitals are shown in the diagrams with no MO indication, therefore this MO 46 is not much delocalised. Instead of that, electrons are mostly localised in their own orbitals. From the comparison of the orbital sizes, the larger p orbitals of Br dominate in the orbital contribution.

Each halpgen atom has an intranuclear node at central position. A nodal plane is passing through the two nodes in the bridging Cl atoms.

Molecular Orbital 48

The main orbital contribution comes from the side-by-side overlap of two parallel p orbitals in terminal Cl. This bonding interaction gives a delocalised MO which is perpendicular to the plane of two terminal Cl and it introduces a pi-analogue system to this MO. The nearby Al doesn't take part in this interaction due to the narrow middle region in the pi-like orbital. Each bridging Cl also presents a p orbital, but since it is orthogonal to the pi-like orbital, they are expected to have no interaction. The rest bondings and antibondings are all weak as orbitals are distant through space. Overall the MO 48 is strong bonding with delocalised MO of the terminal Cl as pi system.

There is an important nodal plane that cutting through 4 intranuclear nodes at 4 terminal atomic centres.

Summary

The above analysis on 5 molecular orbitals reveal the real situation on the orbital shape, size and geometry. Some of the result interpretations even give the information that is not represented by the bond or we ingnored before. A remarkable point is it is possible to have pi framework in the Al₂Cl₄Br₂ molecule and the pi character comes from the pair of bridging and terminal Cl atoms. From the comparision of the conputed MO and the redrawn MO diagrams, the MO theory seems to lack of enough accuracy to show the real orbital interaction in a relatively small-sized molecule. However, the computational method using high level basis sets and pseudo-potentials could reduce the possible errors in constructing the resulted MOs from constituent AOs. Therefore, it would be very helpful to develop Mo theory with computational method as an important tool.

Conclusion

This wiki page populates the quantitative information in details, about the orbital geometry and the orbital interaction characters. The optimisation techniques offers different basis sets on distinct atoms according to their number of electrons and atomic size. B3LYP/3-21G is a relatively low level basis set and is applied to simple molecules comprised by low-mass atoms. While the 6-31G(d,p) basis set can improve the optimisation for larger atoms or more complex molecules. By combining with the introduction of pseudo-potentials, the core electrons in heavy atoms like Br would be taken into account and the modelling would be raised up to a higher level of accuracy.

The main project analysed the role of Lewis acid and base in the Al₂Cl₄Br₂ molecule through the calculation of optimisation, vibrational frequency and molecular orbitals. The IR spectra produced by the computational method include all experimentally active and inactive bands. The number of visible bands is determined by the the point group and the peak intensity. It is demonstrated that for a molecule with low level symmetry, the possibility of having change in the dipole moment would be maximisd and it should give an IR spectrum with a series of peaks. Among the 6 isomers, the one with both Br atoms at terminal positions results a stable dimer form for Al₂Cl₄Br₂. The stretching modes of the Al-Br with Br at bridging or terminal positions are also discussed. It is found that the bridging stretching always needs more energy than terminal. The environment of Al is one of the main factors that affect the magnitude of the stretching frequency value. But due to the limitations of this computational lab, more quantitative data is required to provide a more detailed and valid interpretation on the frequencies. Finally, the molecular orbitals of Al₂Cl₄Br₂ are modified which reveals a more realistic situation especially in the interaction between atomic orbitals. A highlighted point is sometimes Al₂Cl₄Br₂ experiences a pi framework constructed from the interaction between two bridging or terminal Cl atoms. The MO theory seems to be an oversimplication in finding the orbital shape, arrangement and the mutual interactions. The computational optimisation is suggested to be introduced to provide real MO diagrams on the further analysis of the nature or properties of a molecule.

Reference

1. C. D. Silva, O. Proux, J. Hazemann, J. James-Smith, D. Testemale, et al.. 'X-ray Absorption Spectroscopy Study of Solvation and Ion-Pairing in Aqueous Gallium Bromide Solutions at Supercritical Conditions', Journal of Molecular Liquids, Elsevier, 2008, 147, pp.83-95.

2. UCDAVIS Chemwiki: http://chemwiki.ucdavis.edu/Theoretical_Chemistry/Chemical_Bonding/General_Principles/Bond_Energies (assessed February 2015)