Rep:Mod:MeWantA

The Hydrogenation of Cyclopentadiene Dimer

Dimerisation

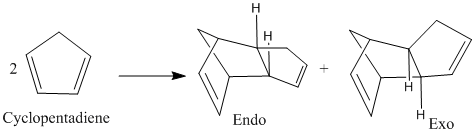
The dimerisation of cyclopentadiene (shown in figure 1) leads to two possible isomers, one called endo and another exo. Molecular modelling of the two isomers was carried out in ChemBio3D. Using molecular mechanics specifically the MM2 force field the energy of the isomers was minimised by changing the geometry. This gave the equilibrium position of both forms of the compound shown in the diagrams on the right. The relative energy of the endo and exo forms and the interactions that make up this number is given in the table to the right.

The lowest energy isomer is the exo one with the endo form being approximately 9 kJmol^-1 higher in energy. The table shows that the majority of this energy difference is found in "torsion" energy. This increase in the torsion energy suggests that groups are forced to twist into a higher energy orientation about bonds. Its is reported that the endo dimer predominates despite being higher in energy. Thus the reaction must be under kinetic control with the endo product having a lower energy transition state. This is as reported in the literature which suggests that the endo form has a transition state about 12kJmol^-1 lower than the exo form.

Energy Comparison

Parameter (kJmol-1)	Exo (1)	Endo (1)
Total Energy	133.38	142.28
Show All Parameters &nbsp &nbsp Bend 86.07 87.37 Stretch 5.35 5.20 Stretch Bend -3.50 -3.50 Torsion 32.06 39.79 vdWaals 11.82 11.55 DipDip 1.58 1.88

Dimerisation

Dimerisation

Exo Isomer (1)

Endo Isomer (2)

Hydrogenation

Dicyclopentadiene (DCP) and its hydrogenation products find a range of uses in the rubber and pharmaceutical industries. DCP can be hydrogenated at either of its double bonds. The product of both hydrogenations were modelled and had their geometries optimised using molecular mechanics specifically the MM2 force field. The minimised equilibrium position of the molecules is shown to the left with the relative energies.

As can be seen the hydrogenation in the norbornene ring (NHCPD) leads to a lower energy isomer than hydrogenation in the pentene ring (PHCPD). The biggest difference between the isomers is caused by the "bend" term which is a result of sp³ carbons not being able to adopt their preferred tetrahedral geometry whilst in the ring systems. The ring strain is apparently higher in both the products as a sp² has bond angles that require less distortion to fit into a ring than an sp³ one does. The carbons in the pentene ring are more strained than in the norbornene ring and thus the change from sp² to sp³ is more destabilising.

It is reported in the literature that the hydrogenation in the norbornene ring happens first and a lot faster than hydrogenation in the pentene ring. This means that the reaction could be either under thermodynamic or kinetic control with the favoured product being lower in energy and having a lower transition state.

Energy Comparison

Parameter (kJmol-1)	PHCPD (3)	NHCPD (4)
Total Energy	154.26	122.38
Show All Parameters &nbsp &nbsp Bend 78.05 54.49 Stretch 5.20 4.72 Stretch Bend -3.14 -2.35 Torsion 53.79 51.98 vdWaals 19.68 12.95 DipDip 0.68 0.59

Cyclopentene Hydrogenation Product (3)

Norbornene-Ring Hydrogenation Product(4)

Sterochemistry of Nucleophillic Additions

Reaction One

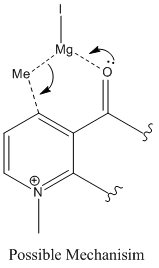
The nucleophillic addition of the grignard reagent to the pyridine ring system proceeds with the stereochemistry shown below. Using molecular mechanics and the MMFF94 force field the stable geometries of the reactant were found and a selection are shown on the right. The different minima were found by putting the 7 and 5 membered rings in different conformations however all the minimisation resulted in geometries with several things in common. The angle between the nitrogen and carbonyl in the peptide is always small to allow maximum overlap between the lone pair on the nitrogen and the pi* on the carbonyl. All conformations preferred to keep the ether oxygen in plane with the pyridine ring to allow some delocalisation into the C-O pi* orbital. When the five membered ring exists in a puckered conformation then the lowest energy conformer was the one with the puckered carbon pointing away from the carbonyl. In all cases the carbonyl was on the opposite side of the ring to the chiral proton. It is the orientation of the carbonyl ring that causes the steroseclectivity of the reaction.

The first step in the addition is the coordination of the magnesium of the Grignard (figure 3) to the oxygen atom, as the oxygen is always on the “top of the compound” (the opposite side of the compound to the proton at the chiral carbon) the Grignard likewise always sits on top of the compound and it is to this side that the methyl group adds.

Reaction Showing Sterochemistry

1st step

Energy/kJmol-1 Angle/degrees Image 246.8 25 240.8 21

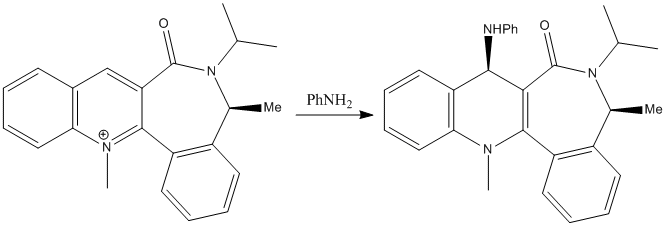
Reaction Two

Using the MMFF94 force field molecular mechanics were used to investigate the stable conformers of the reactant. There is apparently only one stable conformation available to this molecule with the force field producing the geometry shown below and giving an energy of 416.8kJmol^-1. All of the rings capable of being aromatic when planar stay planar as this is very energetically favourable thus the only conformers belong to the seven membered ring. The seven membered ring always minimises to its most stable, boat, conformation. The carbonyl double bond stays roughly planar to the the lone pair on the nitrogen for the same reasons as the previous reactant and because of the geometry adopted on the other side of the molecule to the methly on the chiral carbon adjacent to the lactam group. As in the previous reaction the carbonyl carbon controls the sterochemistry of the reaction however in this example it sterically hinders the approach of the bulky nucleophile causing it to attack on the other side of the molecule resulting in the sterochemistry shown.

Reaction showing sterochemistry

Taxol

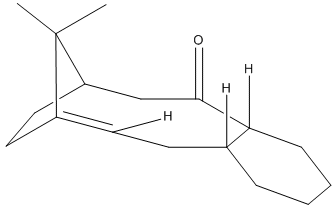
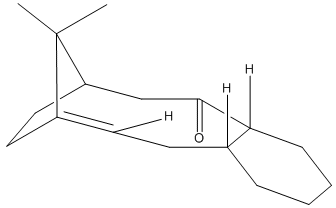
The isomers 9 & 10 show anisotropisim, where rotation about a single bond is kinetically hindered. The isomers had their geometry optimised using molecular mechanics in both the MM2 and MMFF94 force fields. Using both techniques the isomer 10 was found to be more stable than isomer 9 thus would be the larger component in a equilibrium mixture. The largest destablaising factor in 9 (compared to 10) is likely to be the bend away from idea bond angles caused by the inability of the six membered ring to adopt its preferred chair conformation.

The double bond next to the bridgehead is responsible for the molecules being more stable than expected. The molecules are an example of hypersatable alkenes. Hyperstable alkenes are olefins next to bridgeheads in polycyclic systems which are more stable than would be expected as they exhibit reduced bond strain compared to the parent hydrocarbon.

During the minimisation process several local minima were found in the energy, these correspond to different conformations of rings (such as chair and boat for cyclohexane). The lowest energy conformer was found by minimising the energy using a force field manually moving atoms around into more preferable situations and then minimising again. The table below shows the energy of conformation found in the minimisation of molecule 10.

MM2 Minimisation Iterations of Molecule 10

Iteration	Change	Energy\ kJmol-1
1	Initial Conformation	464
2	Six membered ring to chair conformation	440
3	Change geometry of big ring	284
4	Change geometry of big ring	243
5	Six membered ring back to chair	226

Lowest Energy Conformer Molecule MM2 Energy\ kJmol-1 MMFF97 Energy\ kJmol-1 9 232.87 329.78 10 225.93 312.05

Addition of Dichlorocarbene

Dichlorocarbene and peracids are electrophillic reagents and thus attak the most easily acessable electons in a compound which are located in the HOMO. It is impossible for molecular mechanics to predict the regiochemistry of this reaction as it ignores the presence of electrons entirely simply treating each bond as a spring. A semi empirical method was used to map the molecular orbitals of the reactant (with a selection shown below). The geometry of the compound was optimised by molecular mechanics, specifically the MM2 force field before the MOs were calculated using MOPACK with the method PM6.

It can be clearly seen in the molecular orbital diagrams below that the HOMO of the dialkene compound (shown below) has a large amount of electon density on the alkene sin to the chlorine atom. This makes the alkene sin to the alkene the most likley place for a nucleophillic attack.

Molecular Orbitals

HOMO	LUMO	HOMO-1	LUMO+1	LUMO+2
HOMO	LUMO	HOMO-1	LUMO+1	LUMO+2

Using the density functional approach the molecular vibrations of the reactant and its dihydro (at the anti alkene) derivative were calculated. Specifically the Gaussian B3LYP method using the 6-31G(d,p)basis set was used to both optimise the geometry and calculate the vibrations some of which are shown below.

'Vibrations of Dialkene'

C=C Sin	C=C Anti	C-Cl
1757.36 cm-1	1737.07 cm-1	770.89 cm-1

There is a alight reduction in the amount of energy (proportional to the wavenumber of vibration) required to stretch the sin double bond in the hydrogenated product. This can be rationalised in two ways. One: the small amount of election density added to that bond by the anti double bond (now removed) has been lost making the bond easier to distort. Two: the origional stretch resulted in the distortion of the other ring/ compression of the double bond, this is easier now as alkanes are more conformationally flexible than alkenes.

Vibrations of Hydrogenated Product

C=C Sin	C-Cl
1753.76cm-1	779.93 cm-1

Miniproject

My miniproject can be found here