Computational Lab Report

Part 1

Introduction

Cope rearrangement is the [3,3]-sigmatropic shift rearrangement of 1,5-dienes. The transition state at which Cope rearrangement proceeds has been a subject of debate, although the current accepted mechanism of Cope rearrangement is concerted through an aromatic transition state.

Mechanism of 1,5-hexadiene undergoing Cope Rearragement

Optimizing Reactants and Products

There are 27 possible conformations for 1,5-hexadiene to adopt due to its three rotating carbon-carbon bonds. However, there are only 10 energetically unique conformers due to symmetry and enantiomeric relationships. However, in ab initio calculations, the activation energies and enthalpies uses the lowest energy (most stable) conformers as a reference reactant molecule. As a result, the structure of the conformer with the lowest energy must first be determined.

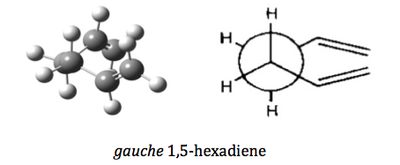
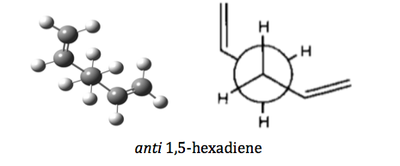
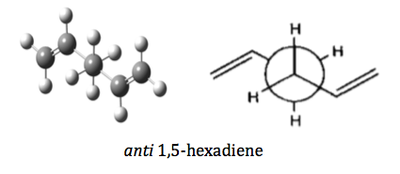
In this exercise, three conformers were optimized using three different levels of theories, namely semi-empirical/AM1, Hatree-Fock/3-21G and B3LYP/6-31G(d). The structure of the three conformers are given as below:

**Structure and Point Group of 1,5-Hexadiene Conformers**
Conformer	Structure	Point Group
gauche 1,5-hexadiene		C₂
anti 1,5-hexadiene		C₁
anti 1,5-hexadiene		C_i

Image of Newman Projection adapted from Rocque et all (see bibliography no.5)

Energy difference between anti and gauche 1,5-hexadiene conformers

The results are tabulated as below:

	Methods and Energies (a.u.)
	Semi-empirical/AM1	HF/3-21G	B3LYP/6-31G(d)
Gauche 1,5-hexadiene (C₂)	0.02945203	-231.69166700	-234.61068822
Anti 1,5-hexadiene (C₁)	0.02818095	-231.69253506	-234.61170276
Anti 1,5-hexadiene (C_i)	0.02816982	-231.69260235	-234.61180027

From the table above, it is apparent that the 1,5-hexadiene with the framework point group of C_i has the lowest energy.

However, it is interesting to note the difference in energy of the gauche conformer (C₂) and anti conformer(C₁. The difference in their respective energies generated using the three methods are tabulated below

	Difference in Energies (a.u.)
	Semi-empirical/AM1	HF/3-21G	B3LYP/6-31G(d)
Difference in Energy	0.00128221	0.00095650	0.00111205
Average Difference Energies (a.u.)	0.00111692 a.u. (2.931 kJ/mol or 0.7 kcal/mol)

Despite using three different methods, the difference in energies between the gauche conformer (C₂) and anti conformer(C₁ is quite consistent, albeit quite small (about ten fold less than that of butadiene). It is postulated that the energy difference is due the steric repulsion of the two enyl groups in close proximity to one another. However, using higher level theories such as MP2 and CCSD(T), Rocque et al. determines that the energies of the 10 conformers are essentially degenerate. Their work also suggested that due to the lack of electron correlation in Hartree-Fock method, 1,5-hexadiene is treated too similarly to a butadiene which leads to poor results.

Geometry difference between anti and gauche 1,5-hexadiene conformers

Using different level of theories, the geometries of the molecule changes slightly. The difference in the structures are tabulated as below:

Conformers and Methods		Bond length (Angstrom)			Bond angle (degrees)
Conformers and Methods		C1-C2	C2-C3	C3-C4	a	b
Gauche	HF/3-21G	1.31564	1.50832	1.55077	124.97390	112.04390
Gauche	B3LYP/6-31G(d)	1.33309	1.50442	1.54815	125.39982	113.63603
Anti C₁	HF/3-21G	1.31608	1.50888	1.55231	124.75456	111.37500
Anti C₁	B3LYP/6-31G(d)	1.33347	1.50403	1.54771	125.24348	112.67108
Gauche	HF/3-21G	1.31627	1.50908	1.55272	124.80187	111.35238
Gauche	B3LYP/6-31G(d)	1.33351	1.50408	1.54808	125.28897	112.68043

Rocque et al. also reported the bond length for C3-C4. Using CCSD(T) theory, his results are as below:

Conformer	Bond length (Angstrom)
Gauche (C₂)	1.517
Anti (C₁)	1.535
Anti (C_i)	1.535

Comparing both bond lengths, it is apparent in the deficiencies in the level of theories and methods used to run these calculations as compared to CCSD(T). While semi-empirical/AM1 method gave a good correlation with the C3-C4 bond length of the gauche conformation, it fails miserably with both the anti conformers. Meanwhile, although HF/3-21G and B3LYP/6-31G(d) is in close agreement with the C3-C4 bond length with CCSD(T), they have the tendency to overestimate the bond length, just as so with the energies.

Vibrational Frequencies of anti 1,5-hexadiene

Using a simple harmonic oscillator model, the vibrational frequencies of a molecule can be calculated by:

where: f = vibration frequency; k = force constant; m = reduced mass

It turns out that the force constant, k is equivalent to the second derivative of the potential energy curve.

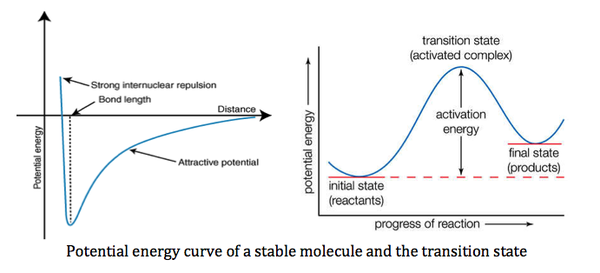
When a molecule is in its ground state (at equilibrium bond length), it has minimum energy. As the molecule vibrates and departs from its equilibrium bond length, the energy increases. Since the potential energy curve for all vibrational modes of the molecule increases, the second derivative would be positive, yielding a positive k and hence a positive and vibrational frequency.

However, in a transition state, the potential energy curve slopes downwards both forward and backwards from the transition state (maximum point). The second derivative would therefore yield a negative k and a negative vibrational frequency.

However, in this case, the anti-hexadiene (C_i) is being optimized hence no negative vibrational frequency should be observed and this is indeed the case.

Optimizing the “Chair” and “Boat” Transition Structures

The transition state at which Cope rearrangement proceeds has been postulated to go either via the chair transition state or the boat transition state. For the kinetically controlled Cope rearrangement reaction, the pathway with the lowest energy transition state would be the preferred mechanism.

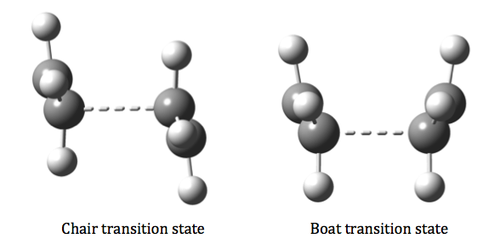
Using different methodology and 3 different level of theories (semi-empirical/AM1, HF/3-21G and B3LYP/6-31Gd), the bond breaking/forming distance of the transition state has been calculated. The vibration frequencies have been checked as well for a negative value to ensure that the structure obtained is indeed a transition state. For simplicity, only the energies of the transition states found by using HF/3-21G and B3LYP/6-31G(d) will be reported.

B3LYP/6-31G(d)
	Chair Transition State			Boat Transition State
	Normal	Freeze Coordinate	QST2	Normal	Freeze Coordinate	QST2
Energy	-234.55698297	-	-	-234.54309288	-	-234.54309290
Imaginary Frequencies	-565.4704	-	-	-530.39	-	-530.37
HF/3-21G
Energy	-231.60280228	-231.60068454	-231.60280215	-231.61932243	-231.619322379	-
Imaginary Frequencies	-839.5045	-840.0922	-839.5045	-817.973	-817.9719	-

The vibration modes of the negative vibrational frequencies are given as below:

Transition State	Frontal view	Side View
Chair conformation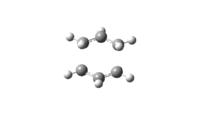
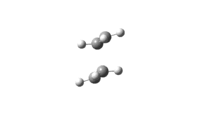
Boat conformation

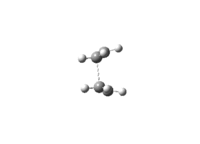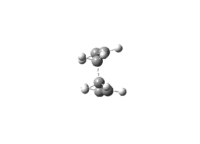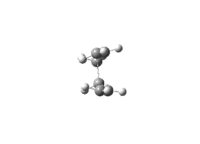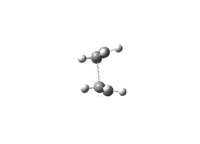
There bond lengths and bond angles of the transition state is characterized in the table below:

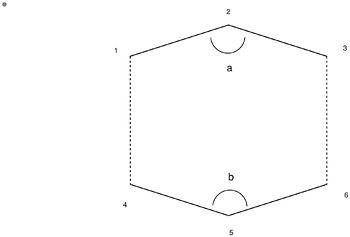
B3LYP/6-31G(d)
	Chair Transition State			Boat Transition State
	Normal	Freeze Coordinate	QST2	Normal	Freeze Coordinate	QST2
C1-C2	1.40754	-	-	1.39319	-	1.39318
C2-C3	1.40759	-	-	1.39324	-	1.39329
a	119.95231	-	-	122.26846	-	122.25770
HF/3-21G
C1-C2	1.38930	1.38935	-	1.38155	1.38143	1.38126
C2-C3	1.38925	1.38930	-	1.38155	1.38143	1.38126
a	120.50523	120.50305	-	121.66467	121.68511	121.67953

Intrinsic Reaction Coordinate

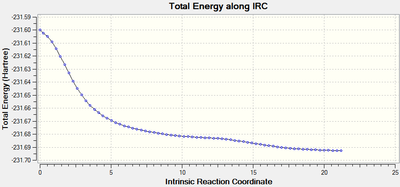
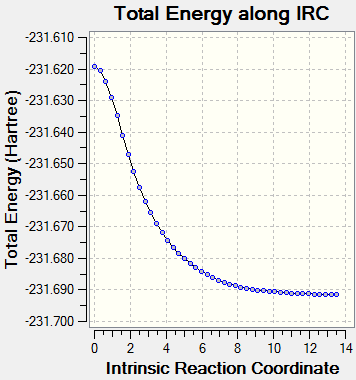
Although the transition state structure has been deduced, Intrinsic Reaction Method needs to run to determine which conformers the transition state will collapse into. Initially, the IRC method was run with N=50 points for both the boat and chair transition state, however, it was observed that a minima has not been achieved.

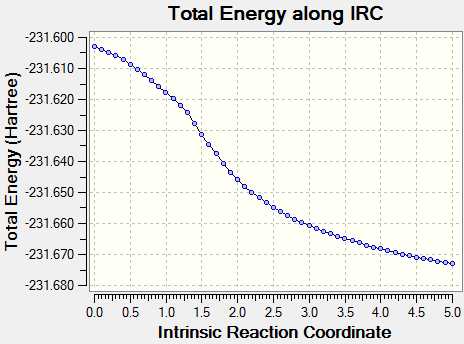
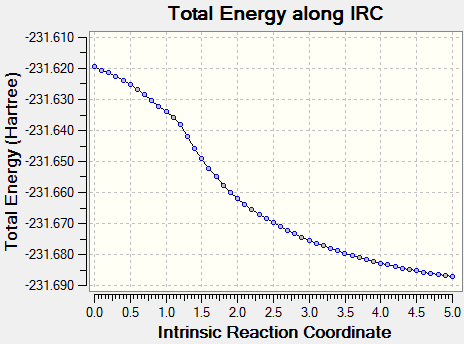
IRC plot of the Boat transition state Conformation (N=50)

IRC plot of the Chair transition state Conformation (N=50)

The problem was circumvented by increasing the number of points taken for the IRC i.e. N=100

Using the first method where the number of points taken is increased to N=100, that boat and chair transition has reached their respective minima. The minima of the chair transition state was found earlier, ending at N=64.

IRC plot of the Boat transition state Conformation (N=100)

Animation of the IRC for the Boat transition state

IRC plot of the Chair transition state Conformation (N=100)

Animation of the IRC for the Chair transition state

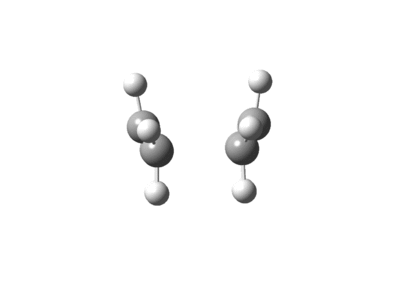
The final structure of the conformers produced by the chair and boat conformations are:

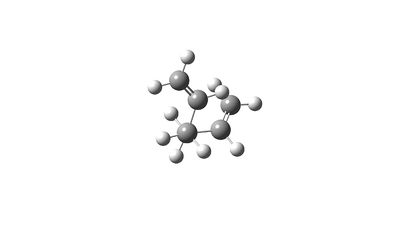
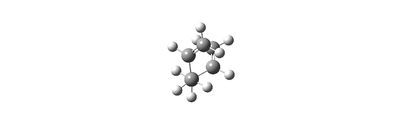
Product of the Boat transition state Conformation(C₁)

Product of the Chair transition state Conformation(C₂)

Summary of Part 1

Summary of energies (in hartree)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619324	-231.466700	-231.461341	-234.556983	-234.414929	-234.409008
Boat TS	-231.600685	-231.450926	-231.445297	-234.543093	-234.402342	-234.396008
*Reactant (anti2)*	-231.692535	-231.539506	-231.532557	-234.611703	-234.469191	-234.461794

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.686	44.689	34.050	33.124	33.5 ± 0.5
ΔE (Boat)	55.585	54.756	41.948	41.281	44.7 ± 2.0

Part 2

Introduction

For a cycloaddition to occur, the orbitals on the molecules must have the right symmetry so that a positive overlap can occur. In this study, 1,3-butadiene and ethene is used to study the reaction of cycloaddition.

In this cycloaddition, the pi orbitals of the ethene will overlap with the pi orbitals of the diene (1,3-butadiene) to form new C-C bonds in a very stereopsecific fashion

The HOMO and LUMO of Butadiene

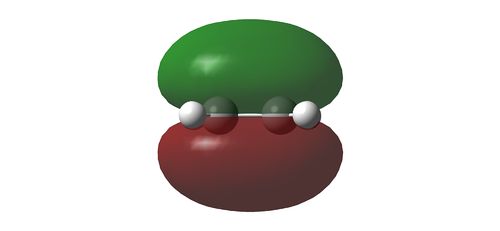
Using HF/3-21G, the HOMO and LUMO of the reactants in a cycloaddition is determined. With respect to a plane of symmetry perpendicular to the molecule, the HOMO of ethene and LUMO of the butadiene is symmetrical while the the HOMO of butadiene and the LUMO of ethene is assymmetrical. Hence, it is the HOMO-LUMO pair of the reactants that will interact with one another. The orbital pairs from the ethene and butadiene are illustrated as below

HOMO of 1,3-butadiene reacting with LUMO of ethene

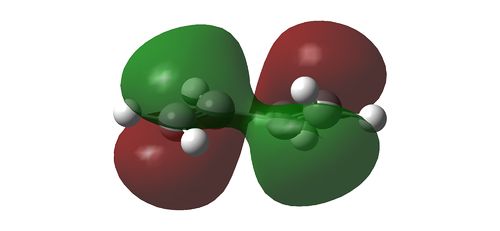
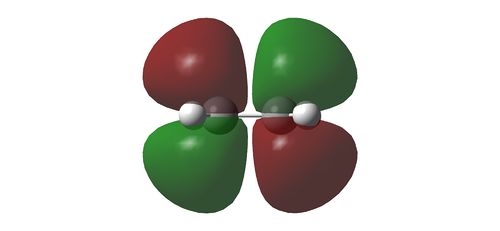
LUMO of 1,3-butadiene reacting with HOMO of ethene

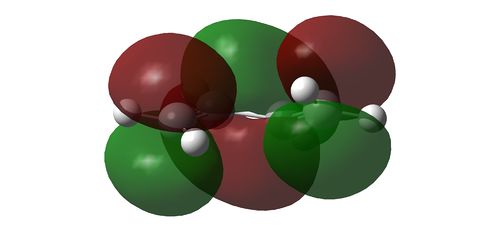
The Transition State of a Cycloaddition Reaction

To find the transition state of the cycloaddition reaction between 1,3-butadiene and ethene, the three level of theories (semi-empirical/AM1, HF/3-21G and B3LYP/6-31G(d)) is similarly employed.

The transition state of the cycloaddition between an ethene and a 1,3-butadiene is as below:

test molecule

The findings are tabulated as below:

Bond lengths and angles	Different Methods
Bond lengths and angles	Semi-empirical/AM1	HF/3-21G	B3LYP/6-31G(d)
Intra-reactant C-C bonds
C1-C2	1.38188	1.36998	1.38303
C2-C3	1.39745	1.39448	1.40719
C3-C4	1.38186	1.37000	1.38305
C5-C6	1.38294	1.37585	1.38596
a	121.18427	121.47260	122.03073
b	121.18293	121.47293	122.03344
Inter-reactant C-C bonds
C1-C5	2.11918	2.20960	2.27224
C4-C6	2.11931	2.20956	2.27269

The typical bond length of an sp³ carbon-carbon is 1.54 angstrom, sp² carbon-carbon bond is 1.47 angstrom while the Van der Waals radii of the carbon atom is 1.70 angstrom. However, in this instance, it is quite surprising to see that all the bond lengths calculated from Gaussian are shorter than the experimental values. This could be due to the fact that the level of theory used to calculate the bond lengths are insufficiently accurate.

In a normal instances, it is expected that the transition state bond length should be longer than normal. This is because as orbitals overlap during the cycloaddition, the electron density would flow from the diene to the dienophile. The loss of electron density would have lead to a decrease in bond order/bond strength.

The Cycloaddition Transition State Vibrational Frequencies

To ensure that it is indeed the transition state of the cycloaddition, the vibrational frequencies were checked and a negative frequency corresponding to -524.8453 was obtaine. The imaginary frequency is synchronous while the least positive vibration frequency (135.54) involves rocking from side to side in an asynchronous fashion. The vibrational mode of the imaginary frequency is illustrated as below:

Stretches that produce the imaginary frequency

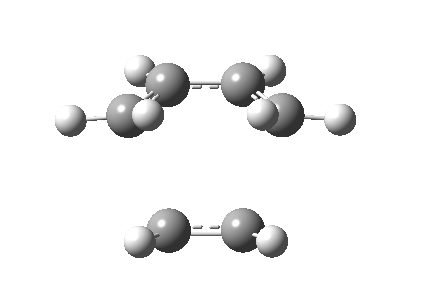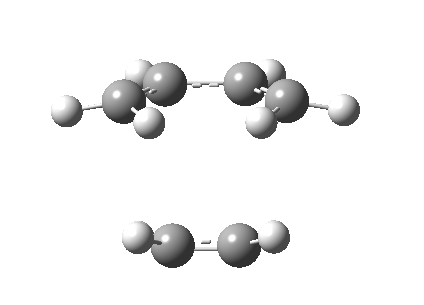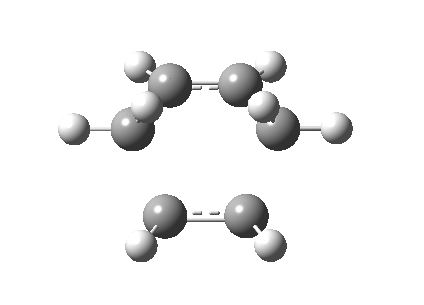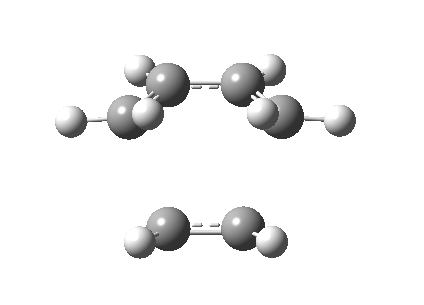
Front view of the imaginary frequency stretch

Stretches that produce the least positive frequency

Front view of the least positive frequency stretch

The Energies of the Cycloaddition Transition State

The energy of the transition state is given as below:

	Semi-empirical/AM1	HF/3-21G	B3LYP/6-31G(d)
Energy of Transition State (a.u.)	0.11165468	-231.60320853	-234.54389654

The Molecular Orbitals of the Cycloaddition Transition State

The LUMO is unsymmetrical while the HOMO is symmetrical.

The HOMO of the transition state (-0.21897 a.u.) was a concern initially because it seems that there is a nodal plane right across there the C-C sigma bonds are suppose to form. Rechecking the Molecular Orbitals showed that there could be a degeneracy of orbitals involve in this instance. There is another orbital that is in very close energy to the HOMO (-0.22106). That orbital is therefore called HOMO2 in this instance. This orbital looks more likely to be involved in bonding as there's a good overlap between the orbitals of the diene and the dienophiles.

The HOMO and the LUMO of the Transition state is given as below:

		LUMO	HOMO 1	HOMO 2
Molecular Orbital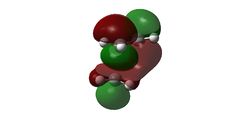
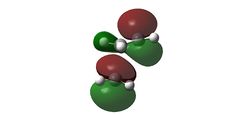
Energy of Transition State	Semi-empirical/AM1	0.02316	-0.32499	-0.32394
	HF/3-21G	0.14241	-0.30087	-0.30292
	B3LYP/6-G1G(d)	-0.00862	-0.21897	-0.22107

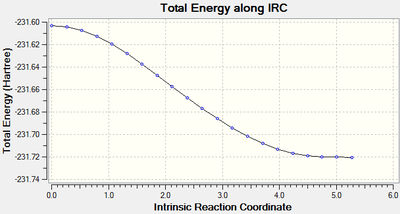
The Intrinsic Reaction Coordinate of the Cycloaddition Transition State

The Intrinsic Reaction Coordinate method is run with using HF/3-21G and N=50. The minimum point was found after N=44 and the IRC plot and its corresponding animation to forming the cycloaddition adduct is as given as below:

Stretches that produce the imaginary frequency

From Transition State to Cyclohexene (Front)

From Transition State to Cyclohexene (Side)

Part 3

Introduction

Transition State Structures of Diels Alder Reaction

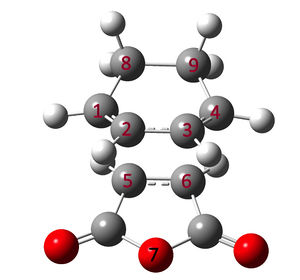
The Transition states of the Diels Alder Reaction between Maleic Anhydride and Cycloehexa-1,3-diene is shown below. The maleic acid can react with the Cycloehexa-1,3-diene with the anhydride functional group pointing towards the diene (endo) or outwards (exo). Both approaches lead to different transition states.

Endo Transition State

Exo Transition State

test molecule

Energy of Transition State Structures of Diels Alder Reaction

The exo transition state and the endo transition state are found by using the Normal and QST2 method. Different level of theories are used in this instance. Their energies are given as below.

Bond Lengths of the Transition States
	Semi-empirical/AM1	HF/3-21G	B3LYP/6-31G(d)
Exo Transition State	-0.05041984	-605.60359125	-612.67931093
Endo Transition State	-0.05150477	-605.61036822	-612.68339678

Bond Length of Transition State Structures of Diels Alder Reaction

	Endo Transition State	Exo Transition State

Bond	Bond Length
Intra-molecular distance
C1-C2	1.39125	1.39146
C2-C3	1.40307	1.40347
C3-C4	1.39127	1.39137
C5-C6	1.39398	1.39791
Inter-molecular distance
C1-C5	2.92139	2.28978
C1-C5	2.26832	2.26838
Through space distance
C-O	3.26907	3.33314

The through space distance between the C and O is a subject of interest. In the exo product, there will be steric repulsion between O7 and C8/C9 while in the endo product, there will be clashes betweem O7 with C2/C3. From the table, it is obvious that the exo product is less sterically hindered as the distance between the C2 and C3 to the Oxygen atom is further than the endo product. Hence, it is expected that the exo product would be the thermally favourable product. However, in reality, the formation of endo products predominates.

Although the exo product is more stable in respect to the endo product, the transition state of the endo product is more favourable due to the contribution from the secondary orbital overlap.

Imaginary Frequency of Transition State Structures of Diels Alder Reaction

Endo Transition State Imaginary Frequency	Exo Transition State Imaginary Frequency
-447.05	-448.48

Molecular Orbitals of Transition State Structures of Diels Alder Reaction

HOMO and LUMO of Endo Transition State

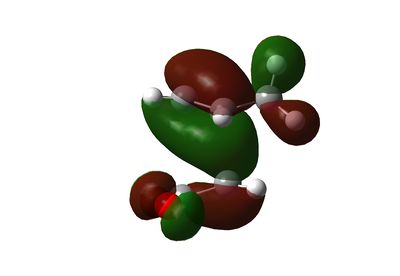
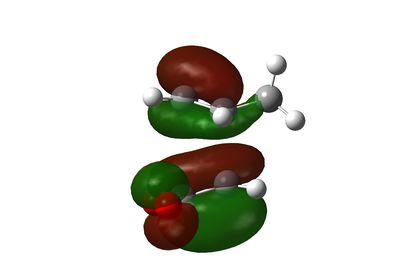
As can be seen on the HOMO of both the exo and the endo transition state, there's a flow of electron froms the diene (two sp² carbon) to the dienophile (one sp² carbon) forming the green bonding MO.

HOMO and LUMO of Exo Transition State

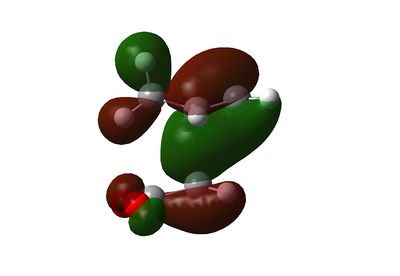
The endo transition state is more energetically favourable due to a secondary orbital effect interaction as can be seen on the HOMO-1 of the endo transition state. Such interaction is absent on the exo transition state.

Secondary Orbital Effect

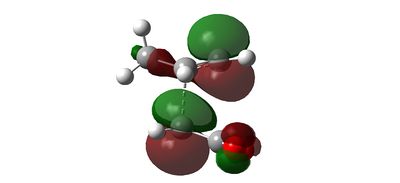
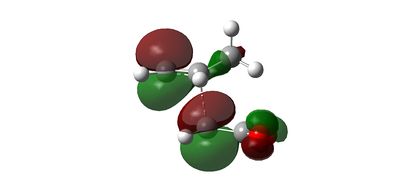
Intrinsic Reaction Coordinate of Transition State Structures of Diels Alder Reaction

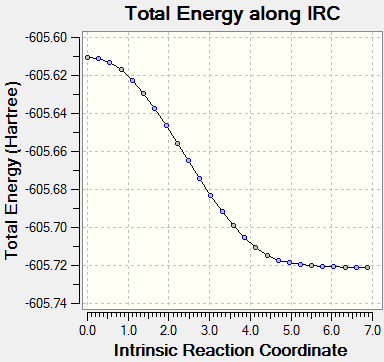
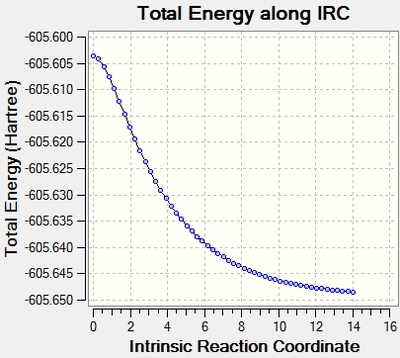
The endo transition state would lead to the endo product while the exo transition state would lead to the exo product. To confirm this, IRC method is employed using HF/3-21G method.

The results are as below:

Endo Transition State IRC	Exo Transition State IRC
-447.05	-448.48

As can be seen from the graph, the exo product is more energetically favourable to form than the endo, but the transition state of the endo is of a lower energy than the exo, making it the kinetic product in the Diels Alder reaction.

In all these calculations, the Gibbs Free Energy is neglected because the endo and the exo both has the same bond breakage and bond formation.

Bibliography

1. J. Phys. Chem. A, 2003, 107 (8), pp 1175–1180

2. J. Am. Chem. Soc., 1995, 117 (6), pp 1783–1788

3. Acc. Chem. Res., 1996, 29 (2), pp 67–75

4. Mol. Phys., 2001, 100(4), pp 441-446