Rep:Mod:Map107 Module 3
Introduction:
The aim of this module is to use gaussien to model transition states of large molecules. This will involve using molecular orbital based methods and solving the schrodinger equation numerically. This is different from the previous methods used, which involved the molecular mechanics force field method. The MM2 method cannot be used as it cannot take into account bonds being broken or made. Instead electron density methods need to be used.
Cope Rearrangement:
The cope rearrangement is a 4n+2 sigmatropic rearrangment that takes place in 1,5 dienes. The reaction process has been the subject of much debate, however the reaction is now commonly accepted to go via a concerted reaction via either a chair or boat transition state. The boat transition state is believed to be several Kcal/mol higher in energy than the chair.
These transition states are to be modelled.
Cope Rearrangement of 1,5 hexadiene:
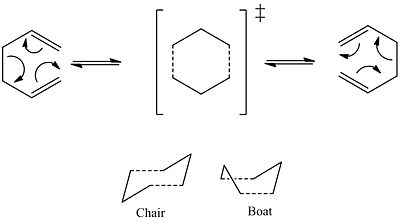
Optimisation Prosses:
The first step is to model the reactant 1,5 hexadiene. 1,5 hexadiene can exist as a number of conformers. The easiest way to model these is to draw the molecule in ChemBio3D. Once drawn the molecules can have the MM2 molecular mechanics applied to them in order to provide a cruede geometry optimisation. The RMS gradient in this optimisation can be set to 0.001 as to produce a fairly good result.
The moleculae can then be saved as a gaussien input folder and opened in gaussviews. this can then have a further optimisation done on it. The following input for the optimisation was used:
# opt hf/3-21g geom=connectivity
Where HF stands for Hartree Fock is the method of calculation and the 3-21g is the basis set and level theory used. A gauche and anti conformer were drawn and optimised. It would be expected that the gauche conformer would be less stable than the anti conformer. The gauche conformer is expected to have more steric repulsion within the molecule, from the hydrogens on the alkene bonds repelling eachother.
Initial Molecules:
note: the numbers refer to the assignments of the conformers in appendix 1:
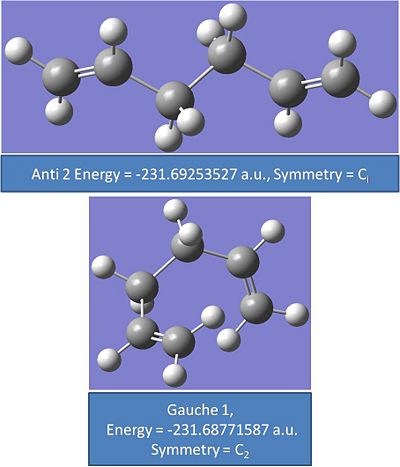
Anti 2:
https://www.ch.ic.ac.uk/wiki/images/0/0b/MichaelP_geom_opt_anti_output_file.txt
Gauche 1:
Another couple of conformers were drawn in order to try and find the minimum energies. These are shown below:
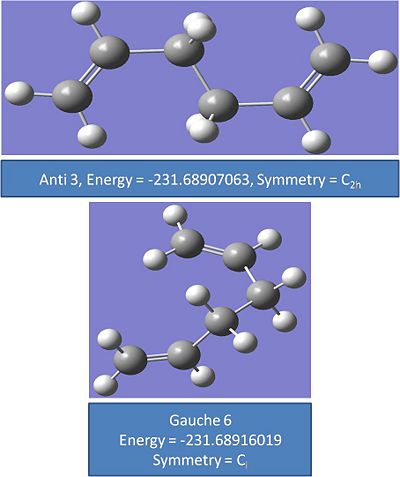
Anti 3:
Gauche 6:
It was found that gauche 6 and anti 2 had the lowest energies. The energies in atomic units cannot be directly compared and the energies need to be converted into joules. However it can be seen that these two conformers are the lowest energy as the energies diverge after 2 to 3 decimal places. as the conversion factor multiplies atomic units by 1 a.u.= 2627.5 kj/mol the relative energie will be different.
It was expected that gauche 6 would be lower in energy than gauche 1 as there will be less steric repulsion between the alkene groups.
The conformers that have been optimised compare well to the values and energies given in appendix 1. All the energies in au compare exactly to 5 decimal places.
Optimising Anti 2:
The anti was optimised using the same method as shown above. The check point file was opened and the energies and point group evaluated. both of these equated to the results in Appendix 1. This molecule was re-geometry optimised with a lower method to see how the methods compare. The optimisation was run with the following input:
# opt b3lyp/6-31g geom=connectivity
Hartree-Fock vs DFT Method:
shown below are images of Anti 2 molecule after it has had its geometry optimised by two differnt methods. The results summaries are also attached.
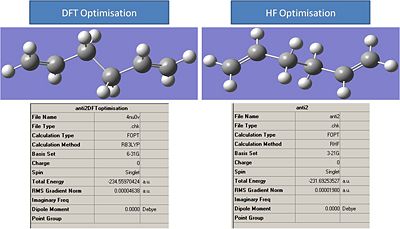
It can be seen from the results that the DFT method led to a much better geometry optimisation than the HF method. However these methods cannot be directly compared as the DFT method used a better basis set than the HF method so would be expected to generate a better result. However the differnce in energy between the two is 7528Kj/mol.
The best way to compare how the geometries have changed is to measure the bond angles.
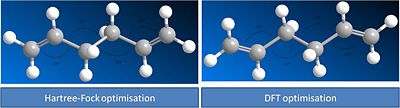
It can be seen from these images that the DFT optermisation leads to larger bond angles. This imply an elongation of the molecule. Initially this seems to be counter intuative that a molecule which has bonds larger than 120 degrees(Sp2) and 109.5 degrees (sp3) bond angles should be more stable. However we have to remeber that the method being used are more advanced than the ideas that are represented by hybridisation theory. The DFT molecule will experience less steric repulsion and hence will be more stable. notice how the bond angle are symmetrical around the centre of the molecule. this explains the centre of inversion and the ci point group.
Vibrational Analysis of 1,5 Hexadiene Anti 2:
As the optimisation that used the DFT, b31lyp method with the 6-31g basis set led to a better geometry optimisation this molecule shall be used in the vibrationa analysis of the molecule. Vibrational analysis is important as it confirms that the molecule is in the global minimum of a potential surface. this works by applying the following theory: The stretching frequencies are derived from the energy surface of a molecule. In classical mechanics the potential of the simple harmonic oscillator can be modelled as potential = 0.5KX2 (hooke's law) where k is the spring constant and x is the change in displacement. The second derivative with respect to displacement of the energy surface will hence be the spring constant. As natural frequency is directly proportional to the spring constant, the frequencies are derived from this. If the frequencies are negative then the spring constant must also be negative and hence be found at the maxima of a potential surface and thus not be the most stable structure. If the spring constant is positive then the molecule is found in the minima of a potential surface. However there can be a number of minima on a potential surface. Hence only if all the stretching frequncies are positive is the molecule found in the global minimum.
It is important to use the same method and basis set when carrying out a vibrational analysis.
Hence the molecule was sent to the SCAN super computer with the following input:
# freq b3lyp/6-31g geom=connectivity
where b3lyp is the method and 6-31g is the basis set.
The most important thing to do when analysing the vibrations is to open the log file to make sure the forces have converged and confirm that there are no large negative frequencies. If these items have failed then the analysis was unsuccesful. If there is one or maybe a number of large negative frequencies it can either mean that the analysis failed or that we are observing a transition state. This would be due to this structure being found at the maximum of a potential surface. By annimating the imaginary frequencies, it can be confirmed if the structure is a transition state or not.
The log file was opened to reveal the following data:
Low frequencies --- -9.3752 -0.0005 0.0000 0.0009 3.6386 13.2047
Low frequencies --- 71.8981 79.9182 116.8572
Diagonal vibrational polarizability:
1.6054663 1.0315041 4.6462939
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- 71.8981 79.9182 116.8511
Red. masses -- 2.7288 2.6323 2.4454
Frc consts -- 0.0083 0.0099 0.0197
IR Inten -- 0.0222 0.1085 0.0000
Item Value Threshold Converged? Maximum Force 0.000113 0.000450 YES RMS Force 0.000046 0.000300 YES Maximum Displacement 0.000442 0.001800 YES RMS Displacement 0.000210 0.001200 YES
It can be seen that all items converged and that all the vibrational frequencies are positive. Hence it can be concluded that the vibrational analysis was sucessful in fonfirming that this geometry optimisation is indeed in the global minimum of the potential surface. note: the low frequencies do not refer to the vibrational frequencies of the molecule but the fixing of the nuclei. these should be as close to 0 as possible however they are hard to fix.
Thermo Chem:
In atomic units.
Sum of electronic and zero-point Energies= -234.416244 (Potential energy at 0K) Sum of electronic and thermal Energies= -234.408954 (Energy at room temperature anf 1atm) Sum of electronic and thermal Enthalpies= -234.408010 (same as a bove but with additional correlation) Sum of electronic and thermal Free Energies= -234.447849 (Includes entropic contribution to free energy)
Boat and Chair Transition States:
The aim of this section is to model the chair and boat transition states in the cope rearrangement. Transition states occur at the maixma of a potential surface. Hence we can expect these transition states to posess a number of imaginary frequencies, as the "spring constant K will be negative" this can cause problem when modelling transition structures. However this section will show the methods that can be employed in modelling transition structures.
C3H5 Fragement:
The first step in modelling the transition states is to draw and optimse a C2H5 fragment. This was drawn in gaussview and optimised with the following input:
# opt hf/3-21g geom=connectivity
Where HF stands Hartree-Fock method and 3-21g was the basi set used.
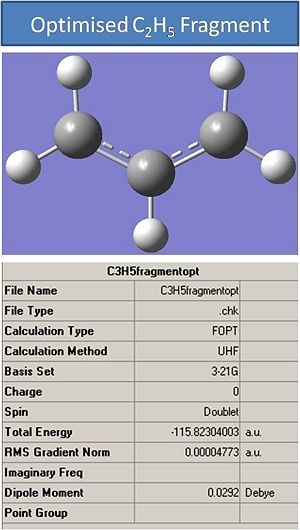
The output file was opened to confirm the optimisation had converged and it had.
Chair Optimisation:
First Chair Transition State Using Hartree-Fock and TS Berny Methods:
The next step was to create an intitial drawing of the chair transition state using two optimised C2H5 fragments. This was achieved on gauss view to produce the image shown below.
This structure was then optimised and had vibrational analysis carried out on it using the following input: note it is important to use the same basis set for this optimisation and vibrational analysis that was used in the fragment optimisation.
# opt=(calcfc,ts,noeigen) freq hf/3-21g geom=connectivity
where HF again stands for the Hartree-Fock Method and 3-21g was the basis set used. Note the additional key words of noeigen and ts. noeigen stops the calculation crashing if there is more than one imaginary frequency calculated (this is expected for a transition state as it is at the maximum of a potential surface) and, ts stands for optimise to a transition state. The calculation was also run with calculate force constantce once.
The calculation should lead to imaginary frequency of -818 cm-1. This vibration should relate to the cope rearrangement.
The output file was opened to confirm that there was only one negative frequency and that the items had convergerd.
The optimised chair transition state indeed possessed an imaginary frequency of -818 cm-1. This was animated to confirm that this corresponded to the cope rearangement.
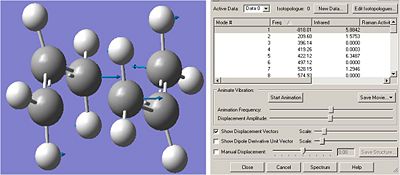
It can be seen from the results that the imaginary frequency does indeed show the cope rearrangement, with the carbon atoms involved in the formation and breaking of a new bond moving towards eachother and away from each other, as they move from one arrangement to the other.
Second Chair Transition State Using The Frozen Coordinate Method:
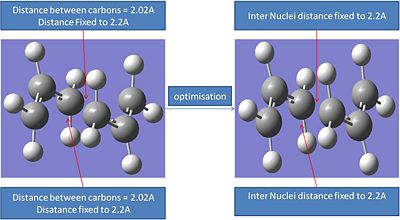
This was a two step process which involved optimising the initial guessed chair structure with the carbons involved in the formation and breaking bonds fixed at a given distance away from eachother (frozen coordinates). Then these bond lengths would be optimised further optimised to produce the optimised chair transition state.
The first step involved re-optimising the guessed chair transition state. The atoms involved in bonding had there internuclei distances fixed to 2.2A. This was achieved through using the freeze co-ordinate method.
the optimisation was run with the following input:
# opt=modredundant hf/3-21g geom=connectivity
The results summary for this optimisation is shown below:
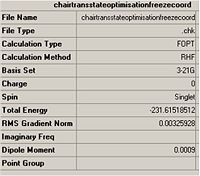
It can be seen that this transition state model is less stable than the first transition state model. this can be seen by the fact that the energies change after 3 decimal points. when this has been converted into relative energies ths shall lead to quite a noticeable difference between the two.
The next step involved optimising the internuclei distance. This would leave the rest of the molecule and just optimise the previously fixed internuclei bond lengths. Again a ts Berny method would be used to optimise the transition state. The optimisation would look to reduce the distance between the bonding/bond breaking carbons such that they were an appropriate disatnce away from each other to form a bond but not to close such that there would be inter nuclei repulsion. This can be achieved by looking for the minimum of the potential curve between these two factors. By editting the reduntant co-ordinates and changing add to dervivative, the programme will look for the point at which the gradient is 0.
The optimisation was run with the following input:
# opt=(ts,modredundant,noeigen) freq hf/3-21g geom=connectivity
The same method and basis set were used, ts stands for transition state, again modredundant refers to the modified reduntant co-ordinates. The noeigen again stops the calculation crashing if there is more than one negative frequency.
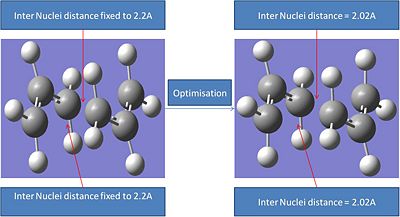
The results summary of this optimisation is shown below:
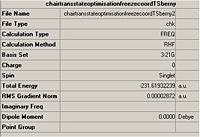
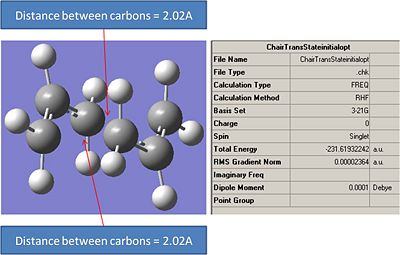
It can be seen that this optimisation process leads to a very similar transition structure to the one produced by the ts Berny geo+vib method. The bond internuclei distance has bee reduced from 2.2A to 2.02A. The main differences in the different optimisation processes is that the first optimisation lead to a fractionally lower energy transition ste. However when the relative energies of these transition states are compared the difference between the two is so small that it probably falls within the error of the calculation.
Third Chair Optimisation:
The chair product was optimised a third time to see how the imaginary stretching frequency and to see how the transition state energy would vary if the optimisation was run with a higher method and basis set. The opt+vib ts berny method (the same method used in the first optimisation) was used to optimise this transition state.
The input is shown below:
# opt=(calcfc,ts,noeigen) freq ub3lyp/6-31g geom=connectivity
As it can be seent the b31yp method was used, as was the 6-31g basis set.
The log file was opened to check that the items had converged and to check the value of the low frequency.
Low frequencies --- -561.9689 -0.0005 -0.0003 0.0010 21.5810 23.2899
Low frequencies --- 40.4194 192.2507 259.4782
****** 1 imaginary frequencies (negative Signs) ******
Diagonal vibrational polarizability:
6.9623465 1.7165150 0.4724248
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- -561.9689 192.2507 259.4513
Red. masses -- 10.2898 2.1910 7.9933
Frc consts -- 1.9146 0.0477 0.3170
IR Inten -- 0.0406 0.7342 0.0000
Item Value Threshold Converged? Maximum Force 0.000065 0.000450 YES RMS Force 0.000020 0.000300 YES Maximum Displacement 0.000877 0.001800 YES RMS Displacement 0.000309 0.001200 YES
As it can be seen from the results all items converged. Hence the optimisation was succesful. The magnitude of the imaginary frequency has decreased. This is due to the use of a superior method and basis set.
The molecule is shown below. The imaginary frequency has been annimated to confirm that it still shows the cope rearrangement.

It can be seen from the picture above that the energy of the molecule has been significantly reduced, and that the vibrational frequency observed does indeed equate to the cope rearrangement.
Interestingly the internuclei distance between the two carbons involvolved in making and breaking bonds has increased from 2.02A to 2.036A.
Boat Optimisation:
First Boat Optimisation:
To model the boat transition structure the QST2 method was used. This process involves modelling the reactants and products of a reaction and then gaussien looks into the transition structure that could have occured to lead from the reactanst to the products.
The first step is to open up the geometry optimised anti2 1,5 hexadiene. The molecule that had been optimised using the b3lyp method and 6-21g basis set was chosen for this task. The molecule was opened and numbered as a reactant. This was achieved through manually editting the labels. The molecule was then copyed and translated so that it looked like the product. This product was renumbered so that the molecules looked like the below picture. The reactant is on the left the product is on the right.
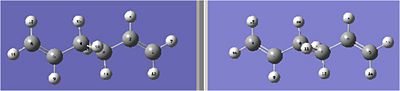
note: it is very important to number all the carbons and hydrogens correctly otherwise the method will fail.
Once this was done the transition state was found and optimised using the following input:
# opt=qst2 freq b3lyp/6-31g geom=connectivity
as it can be seen the opt=qst2 refers to the method involved in finding the transition state.
This optimisation was bound to fail and, not generate the boat transition state. This makes use of hammonds postulate in that the products resemble the transition state in which the reaction procceeded by. Hence the chair transition state would be formed from this optimisation. Indeed it was. This is shown below, however it is interesting to note that the optimisation worked successfully and that the energy, low frequency and inter nuclei distances observed match those produced in the third chair optimisation.
Low frequencies --- -561.9642 0.0003 0.0007 0.0008 20.9316 23.3509
Low frequencies --- 40.3058 192.2508 259.7635
****** 1 imaginary frequencies (negative Signs) ******
Diagonal vibrational polarizability:
6.9798593 1.7153165 0.4724627
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- -561.9642 192.2508 259.7371
Red. masses -- 10.2898 2.1904 7.9994
Frc consts -- 1.9146 0.0477 0.3180
IR Inten -- 0.0377 0.7340 0.0000
Item Value Threshold Converged? Maximum Force 0.000054 0.000450 YES RMS Force 0.000012 0.000300 YES Maximum Displacement 0.001807 0.001800 NO RMS Displacement 0.000574 0.001200 YES
Interestingly one item failed to converge however this was deemed to be non important as this was a "test" optimisation and the RMS Force and Maximum force had converged.

The inter nuclei bond distance observed = 2.035A. Again the imaginary frequency observed equates to the one expected for the cope rearrangement.
Second Boat Optimisation:
With the first optimisation failing, adjustments had to be made to the structures of the products and reactant to make them resemble the boat transition state. This involved changing the dihedral angle of the central 4 carbons to 0 and modifying the bond anle between carbons 2-3-4 to 100degrees. This led to the following structures, with the reactant on the left and the product on the right.
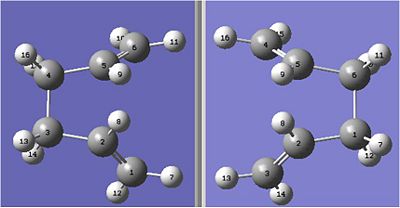
These molecules were again optimised using the QST2 method and the following input:
# opt=qst2 freq b3lyp/6-31g geom=connectivity
Again the b3lyp method was used with the 6-31g basis set.
upon optimisation the log file was opened to confirm the optimisation had workes successfully.
Low frequencies --- -504.3546 -13.9471 -0.0007 -0.0005 -0.0005 12.8279
Low frequencies --- 19.9595 136.0659 261.4431
****** 1 imaginary frequencies (negative Signs) ******
Diagonal vibrational polarizability:
0.9954895 4.5582433 0.6132087
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
B1 A2 A1
Frequencies -- -504.3539 136.0287 261.4431
Red. masses -- 8.9678 2.2859 6.7441
Frc consts -- 1.3440 0.0249 0.2716
IR Inten -- 1.3240 0.0000 0.2660
Item Value Threshold Converged? Maximum Force 0.000010 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.001025 0.001800 YES RMS Displacement 0.000225 0.001200 YES
As it can be seen, all items converged and there is only one large imaginary frequency. this implies that this is indeed a transition state. The graphical image of the molecule shows that this is the boat transition state.
The imaginary frequency occurs at -504cm-1. This is less than the negative than the one produced for the chair transition state.
The results summary was opened to determine the energy of this transition state, and the imaginary vibration was annimated to confirm that this is the vibration expected from the cope reaarangement.
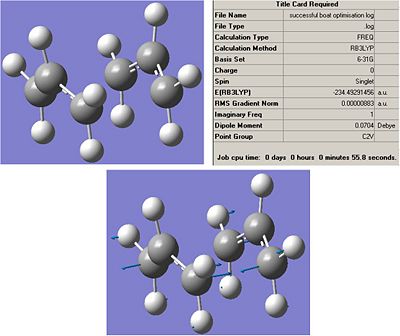
It can be seen that the imaginary frequency is the one that relates to the cope rearrangment. the energy of this transition structure is infact much larger than the energy of the chair transition structure, with the change in energy occuring at the first decimal point. when the relative energies are calculated this will lead to a large difference in energy.
The inter nuclei distances between the carbons forming/ breaking a bond is 2.25A. This is significantly larger than the distance of 2.035A observed in the chair. This is one of the reasons the boat transition structure is higher in energy.
Calculating Chair and Boat IRC:
The transition states have been modelled successfully however they do not tell us about the structures of the products which formed them. In order to find out which reactent forms each particular transition state an IRC (Intrinsic Reaction Co-ordinates) calculatation needs to be run. This calculation works buy starting at the transition state on the potential curve and then takes small deviations in the geometries of the transition states as to minimise the energy. This process continues until a minimum is reached. At this point the starting Product/ Reactant should have been found.
As this reaction is symmetrical, the process only needs to run in one direction, as the product is just the mirror image of the reactant and visa versa.
The IRC does not always find the optimium geometry of the reactant molecule and this is due to the process not having enough iterations. Once the IRC has run there are three methods that can ensure that the reactant is found. 1. Run the IRC with more iterations so that the global miinimum is found. 2. run a geometry optimisation on the last geometry found. Provided this is near a minimum the reactant geometry. 3. Make gaussien calculate the force constants for each iteration. this is the most accurate method however requires the most computational power.
Chair IRC:
The chair IRC was first run with 50 iterations. The Global minimu was not found. So it was decided to re run the IRC with it calculating the force constants for every iteration. The results are shwn below
IRC 50 Iterations:
Calculation input:
# irc=(forward,maxpoints=50,calcfc) ub3lyp/6-31g geom=connectivity
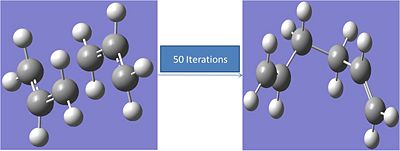
The carbons not forming a bond move from 2.036A apart to 4.52A. The energy of the final structure is -234.5587a.u.
Calculating Force Constants Method:
The process was repeated with the force constants being calculated at each iteration. The calculation was run with the following input:
# irc=(forward,maxpoints=50,calcall) ub3lyp/6-31g geom=connectivity
This calculation took 48 iterations. The results are shown below:
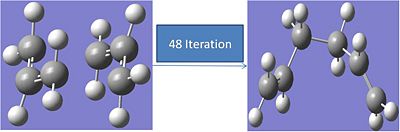
The carbons not forming a bond move from 2.036A apart to 4.52A The energy of the final structure is 234.5587a.u.
Boat IRC:
The Boat IRC was first run with 50 iterations. The Global minimum was not found. So it was decided to re run the IRC with it calculating the force constants for every iteration. The results are shwn below:
50 Iterations:
Calculation input:
# irc=(forward,maxpoints=50,calcfc) rb3lyp/6-31g geom=connectivity

The carbons not forming a bond move from 2.25A apart to 4.53A. The energy of the final structure is -234.55112a.u.
Calculating Force Constants Method:
The process was repeated with the force constants being calculated at each iteration. The calculation was run with the following input:
# irc=(forward,maxpoints=50,calcall) rb3lyp/6-31g geom=connectivity
This only took 25 iterations. The results are shown below:
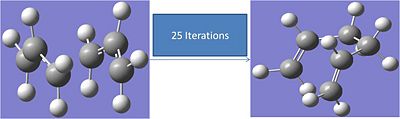
The carbons not forming a bond move from 2.25A apart to 3.345A The energy of the final structure is -234.5452a.u.
Analysis of IRC:
IRC is not a perfect method, a none of the methods produce really accurate results. The results of the two different methods compared are interesting as the energies of the molecules predicted form the calculating force constants methods are fractionally higher. this could imply the calculation was not suceesful or that the method needs have further improvements made to it.
However it is possible to determine the structures of the molecules from which these transition states occur from, from the graphical representations generated. The Energies of these molecules cannot be directly compared, these IRC were run on a higher method and basis set than those in the appendix.
The Chair transition state occurs from the gauche 2 conformer.
The Boat transition state occurs from the gauche 3 conformer.
This was confirmed by re-optimising the final IRC optimisation for each output. The optimisations were run with the following inputs in order for there to be comparable results to the appendix:
# opt uhf/3-21g geom=connectivity
Chair:
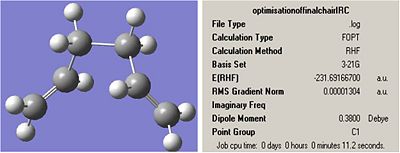
note: the energy is the same as the energy of the gauche 2 in the appendix.
Boat:
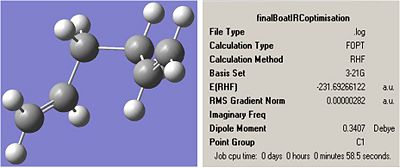
note: the energy is the same as the energy of the gauche 3 in the appendix.
Calculating Activation Energies:
The boat and chair transition states have been optimising using the b31yp method and 6-31g basis set. These energies shall be compared to the anti2 1,5 hexadiene which is the energetically most stable conformer in order to determine the activation energies.
The log files were opened to find the appropriate data:
Anti 2:
Sum of electronic and zero-point Energies= -234.416244 Sum of electronic and thermal Energies= -234.408954 Sum of electronic and thermal Enthalpies= -234.408010 Sum of electronic and thermal Free Energies= -234.447849
Chair:
Sum of electronic and zero-point Energies= -234.362683 Sum of electronic and thermal Energies= -234.356768 Sum of electronic and thermal Enthalpies= -234.355824 Sum of electronic and thermal Free Energies= -234.391613
Boat:
Sum of electronic and zero-point Energies= -234.351358 Sum of electronic and thermal Energies= -234.345054 Sum of electronic and thermal Enthalpies= -234.344110 Sum of electronic and thermal Free Energies= -234.380124
| Molecule/Transition State | 0K Energy/a.u. | RT Energy/a.u. | Differnce at 0K in Energy/a.u. | Activation Energy at 0k/Kcal/mol | literature activation energy at 0k | Experimental at 0K | Difference at RT in Energy/a.u. | Activation Energy at RT/Kcal/mol | Literature activation energy at RT |
|---|---|---|---|---|---|---|---|---|---|
| Anti 2 | -234.416244 | -234.408010 | N/A | N/A | N/A | N/A | N/A | ||
| Chair Transition State | -234.362683 | -234.355824 | 0.053561 | 33.48 | 33.17 | 33.5 +/- 0.5 | 0.052186 | 32.6 | 33.17 |
| Boat Transition State | -234.351358 | -234.344110 | 0.064886 | 40.56 | 41.32 | 44.7 +/- 2.0 | 0.0639 | 39.95 | 41.32 |
It can be seen that the activation energies at 0k fit well to literature and relativly well to experimental values. The activation energies at RT do not fit so well with literature, however they are still pretty close.
It can be seen that the activation energy for the cope rearrangement is lower if the reaction proceeds through the chair transition state. The difference in activation energy at 0K between the two transition states is 7.08kcal/mol.
This fits well with the theory presented at the begining of the section. The inter nuclei distances between the carbons forming/ breaking a bond is 2.25A in the boat transition structure. This is significantly larger than the distance of 2.035A observed in the chair transition structure. This is one of the reasons the boat transition structure is higher in energy.
Modeling The Diels-Alder Reaction:
A Diels-Alder reaction is a pericyclic cyclo addition reaction which involves 4n+2 electrons. The reaction takes place with a dien and a dienophille. The reaction results from the overlap of 4 p orbitals, 2 on the dien and 2 on the dieneophille. The reaction takes place when the HOMO on the dienophille interacts with the LUMO of the diene. This part will look into modelling this reactivitiy and the interactions between HOMO and LUMO frontier orbitals.
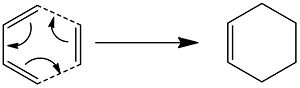
Both cyclo additions being modelled are 4n+2 electron thermally aloud reactions. This means that both are supra facial and lead to Dis rotation.
Cyclo additions can often be stereoselective. This is is due tot the stability of the transition state through which the reaction proceeds. Invariable the endo product is the preferred product, even if the product itself is less stable than the exo product. This is due to the endo transition state being lower in energy than the exo transition state. This has given rise to the endo rule.
when modelling these reactions hammonds postulate shall be applied (the transition state resembles the structure of the product)when drawing these transition states. Through modelling the transition state and the products, it shall be shown that the endo rule is true for certian reactions.
Diels-Alder of Ethene and Butadiene:
The first step in modelling the butadiene transition state was to model the reactants and generate there MO's to see the interacting orbitals. Stereoselectivity could be ignored as ethene was being used as the dienophille, and this molecule is perfectly symmetrical.
The structures were initially drawn in ChemBio3D and had an MM2 optimisation run on them, where the rms was set to 0.001. the resultant structures were exported to gaussien and re-optimise and had there MO's predicted using the semi empirical AM1 method.
Initial Optimisation and MO's
The gaussien calculations were run with the folowing input:
# opt am1 geom=connectivity
The results are shown below:
This method was used so that the MO's of the reactant molecules could be generated at the same time as the optimisation, rather than producing an accurate optimisation and running an NBO analysis later.
The geometries of these molecules were compared:
Butadiene:
C-C bond length = 1.45A
C=C cond length = 1.34A
C=C-C bond angle = 125.7 degrees
Ethene:
C=C bond length = 1.33A
The Mo's of these molecules were generated in gaussien. there symmetries were analysed and are hence shown below:
Butadiene:
note: energies are in atomic units and the black line refers to a plane.
Ethene:
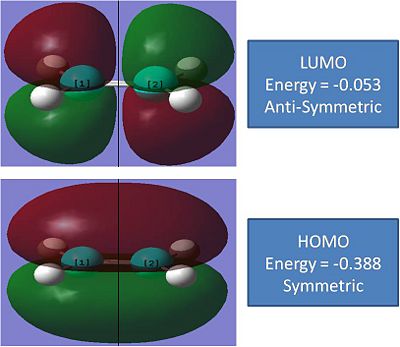
note: energies are in atomic units and the black line refers to a plane.
From the MO's it can be concluded that the iteracting orbitals in this reaction will be the anti-symmetric LUMO on the Butadiene, which shows a pi bond and 2 P orbitals, and the symmetric HOMO of the ethene, which shows a pi bond.
Optimising Reactants with a Better Method and Basis Set:
With the molecules optimised using the se i empirical Am1 method, it was decided to optimise them using the b3lyp method and 6-31g basis set. The molecules were optimised with the following input:
# opt rb3lyp/6-31g geom=connectivity
The log files were opened to confirm the optimisations had worked sucessfully:
Butadiene:
Item Value Threshold Converged? Maximum Force 0.000102 0.000450 YES RMS Force 0.000038 0.000300 YES Maximum Displacement 0.000807 0.001800 YES RMS Displacement 0.000272 0.001200 YES
Ethene:
Item Value Threshold Converged? Maximum Force 0.000248 0.000450 YES RMS Force 0.000150 0.000300 YES Maximum Displacement 0.001480 0.001800 YES RMS Displacement 0.001044 0.001200 YES
As it can be seen both optimisations worked sucessfully.
The molecules still looked extremely similar to those optimised using the AM1 method. However the geometries and energies had changed and these were recorded and noted below:
Butadiene:
Energy =-155.953825a.u.
C=C bond length = 1.34A
C-C bond Length = 1.47A
C=C-C bond angle = 127.1 degrees
Ethene:
Energy = -78.572a.u.
C=C bond length = 1.34A
It can be seen that the geometries have changed slightly. The most noticeable differences are hat the butadien C-C bond has increased in length, as has the C=C-C bond angle.
Optimisation of Transition Structure:
From the previous exercise, it was decided to run a geometry + frequency analysis and minmise to a transition state using the TS Berny method.
It was decided to use this method, as all the methods used produced similar results however this seemed to be fastest and the simplist. The results from this method also seemed fairly accurate.
The optimised molecules were copied and pasted into a new gaussview winow, and poisitioned to resemble the transition state. The ethen molecule was placed 2.2A away from the butadiene molecule such that the initial guess structure looked like the one below:
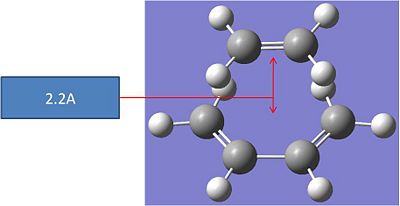
This initial structure was optimised using the following input:
# opt=(calcfc,ts,noeigen) freq rb3lyp/6-31g geom=connectivity
note that the opt=noeigen was included.
The log file was opened so that the vibrations could be analysed. It was expected that there would be a single large negative frequency that would show the transiton state and the vibration associated with it.
Low frequencies --- -534.6118 -6.3374 -0.0009 -0.0007 0.0004 10.9171
Low frequencies --- 18.6477 139.6774 205.4030
****** 1 imaginary frequencies (negative Signs) ******
Diagonal vibrational polarizability:
3.5175582 3.1773127 1.1153819
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- -534.6116 139.6250 205.3884
Red. masses -- 8.1833 2.1713 3.9885
Frc consts -- 1.3780 0.0249 0.0991
IR Inten -- 6.7589 0.8066 1.2760
Indeed a single large low frequency was observed at -534.6cm-1. The frequency was thus annimated on gaussview, to confirm that it was associaed with the transition state.
As it can be seen the imaginary vibration does indeed equate to the transition state, with the ethene carbons moving backwards and forwards towareds the carbons on the butadiene that are involved in forming the new bond.
The energy of this transition state is -234.49456a.u.this is significantly larger than the combined energies of the reactants(-234.525825a.u.)with the energy varying after 1 decimal place.
The geometry of the transition state has also changed. Note how both the butadiene and ethene have gone from being planar (sp2) hybridized carbons with a dihedral angle 0f 0 between the carbons, to being bent at a dihedral angle of -160 degrees. This shows the transition from the reactants to the products, which are sp3 hybridised.
The bond lengths have also changed. The C=C bonds have increased in length, as they prepare to become single bonds, while the butadiene C-C bond has decreased in length as it prepares to become a double bond. This is shown below.
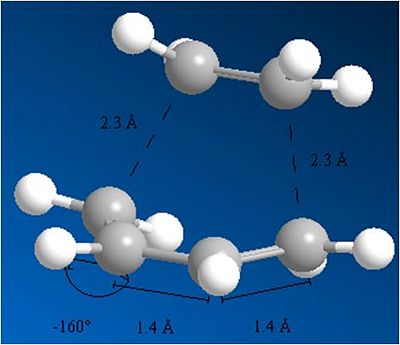
note how all the bond lengths are 1.4A. A Typical sp3 carbon bond length is 1.54A and a typical sp2 carbon bond is 1.34A. So this lies somewhere in the middle which would make sense for a transition state.
Molecular Orbital Analysis of the Transition State:
With the transition state sucessfully optimised the molecular obitals of the transition state could be calculated. This was achieved through running an nbo analysis of the transition state.
The transition state was submitted to gausien with the following input:
# rb3lyp/6-31g pop=(nbo,full) geom=connectivity
The same method and basis set was used. Note the additional pop=(nbo,full) which turns on the nbo analysis:
The calculation was run and the check point file opened. the following results were recorded:
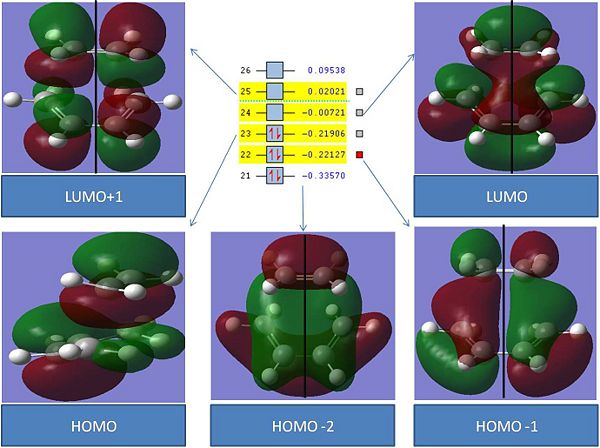
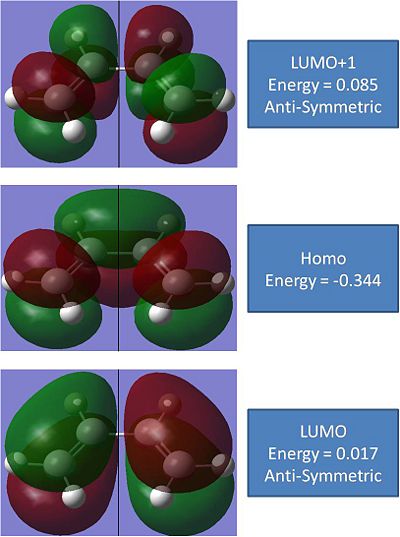
The MO's are very interesting. The first notable thing is that the LUMO has a negative energy. This means that if electron density is placed in this orbital it would stabalise the transition state. Most of the MO's reveal information on the atoms that are forming/breaking new bonds.
The HOMO-2 in the transition state is also interesting as it seems to show the resultant orbital of the symmetric ethene Homo and a Butadiene orbital. This orbital is Symmetric
The HOMO-1 in the transition state appears to be due to the interation between the anti symmetric LUMO of buadiene and the anti symmetric LUMO of Ethene. This implies that these bonds are breaking in order to form new bonds. This orbital is anti-symmetric
The HOMO does not reveal a vast amount of information about the reaction. This orbital is symmetric
The LUMO is very interesting as it seems to be due to the interaction between the ethene symmetric HOMO and the symmetric butadiene LUMO. Interestingly this MO has not occured through the overlap of the nodes that look like p orbitals on the Butadiene with the ethen home, but rather the two pi bonds have overlapped. This implies that electron density in the ethen HOMO will move from the ethene to the C-C single bond on butadiene. This reflects what happens in the reaction. Futhermore, as this LUMO is negative in energy, it implies that this process is favourable. This orbital is symmetric
The LUMO +1 does not reveal any more information. This orbital is anti-symmetric
This NBO analysis has been very interesting. Chemical reactions cannot occur if orbital symmetry is broken however this modelling exercise has demonstrated how orbitals of the same symmetry combine to create new transition state orbitals also with the same symmetry.
From this we can conclude that this reaction is favourable and will happen.
Diels-Alder Reaction Involving Maleic Anhydride and Cyclohexa-1,3-diene:
The aim of this section was to model the regioselectivity of this cycloaddition reaction. As mentioned previously, the endo rule predicts that the endo product will be the major product of the reaction due to the endo transition state being lower in energy. Hence, in this section the two transition states will be modelled in order to prove that the endo transition state is lower in energy than the exo transition state. Then the reasons for this shall be examined.
Optimising the Endo and Exo Transition States:
The Products of the reactions were initially drawn in ChemBio3D. Using hammonds postulate that the transition states will resemble the products, the new carbo carbon single bonds were deleted. The double bonds were reintroduced, and a MOPAC AM1 calculation was run on them in ChemBio3D. This generated the initial structures.
These were then exported to gaussview. Again the geometry + frequency optimise to a transition state (TS Berny)method was used for the same reasons as mentioned previously.
The molecules were submitted to the SCAN computer with the following inputs:
# opt=(calcfc,ts,noeigen) freq b3lyp/6-31g geom=connectivity
The Log files were opened to confirm that the optimisations had worked. This could be achieved through analysing the Low frequencies. As these are transition states a single large imaginary frequency is expected.
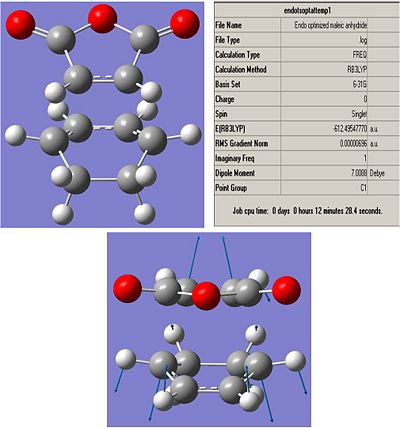
Endo:
Low frequencies --- -446.8430 -13.6030 -4.0215 -0.0010 -0.0009 -0.0008
Low frequencies --- 9.0611 60.4301 120.7955
****** 1 imaginary frequencies (negative Signs) ******
Diagonal vibrational polarizability:
17.1946801 27.5441926 7.8282274
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- -446.8426 60.4216 120.7708
Red. masses -- 7.5221 4.5384 5.9032
Frc consts -- 0.8849 0.0098 0.0507
IR Inten -- 1.4720 1.5604 0.3839
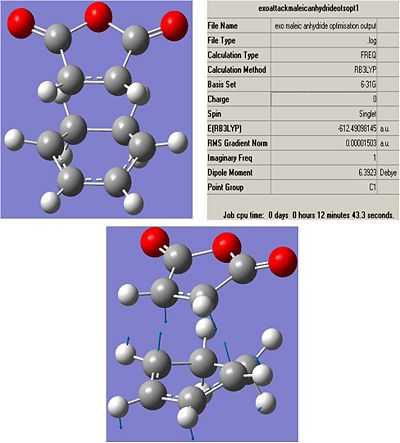
Exo:
Low frequencies --- -448.0037 -13.5535 -11.1369 -0.0008 0.0001 0.0005
Low frequencies --- 5.1405 49.3373 109.1754
****** 1 imaginary frequencies (negative Signs) ******
Diagonal vibrational polarizability:
18.0033062 21.1551187 8.0461872
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- -448.0037 49.1661 109.1723
Red. masses -- 7.7351 4.5706 5.7054
Frc consts -- 0.9147 0.0065 0.0401
IR Inten -- 6.2682 0.6361 0.0209
On both occasions the optimisations worked first time and, returned a single large negative frequency. This was annimated to confirm that it equated to the vibration expected for the cyclo addition. The results are shown below:
ENDO:
EXO:
The vibrations did indeed correlate to the ones expected for the reaction, with the carbons involved in making/breaking bonds moving backwards and forwards towards eachother. Both transition stes had an imaginary frequency of -448cm-1. The energies of the transition states were compared. This is shown below:
| Molecule | Energy/a.u. | Energy/Kj/mol |
|---|---|---|
| Endo | -612.4954777 | -1608106.9 |
| Exo | -612.49098145 | -1608095.1 |
The difference in energy between the two transition states is 11.8Kj/mol. This is a significant amount of energy.
The geometries of the molecules were also compared:
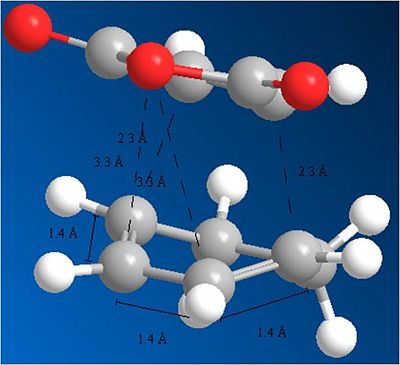
Endo:
Exo:
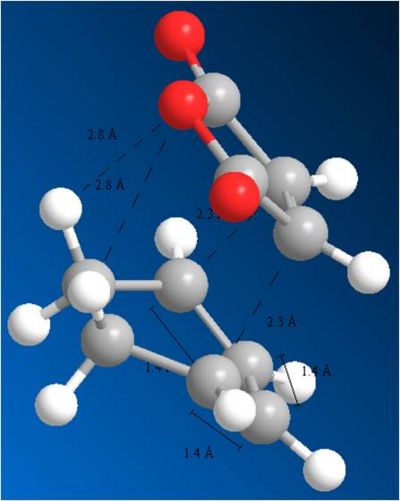
Again, the observations made on the change in geometries for the cyclo addition with Butadiene and ethene apply to this reaction. It can be seen that the starting molecules deviate from there planar structures and a dihedral angle of 0 degrees between the carbons, to a structure where the dihedral changes to 166 degrees. this reflects the transition from sp2 to sp3. The bond lengths have also all changed. They are now all the same length. In the case of the double bonds, the bond lengths have increased, as they prepare to become single bonds. in the case of the C-C single bond, its bond length has decreased as it prepare to become a double bond.
Through analysis of the geometries, it can be shown why the Exo transition state is higher in energy. This is due to more steric interaction with the hydrogens which the maleic anhydride comes above as it attacks the Cyclohexa-1,3-diene. The distance between the maleic anhydride and these hydrogens is 2.8A. In comparison to the endo attack, there is no steric interaction with hydrogens, and the closest atoms are 3.3A away. This explains why the Endo transition state is les strained and more stable. This helps in explaining the selectivity of the reaction.
NBO Analysis of Transition States:
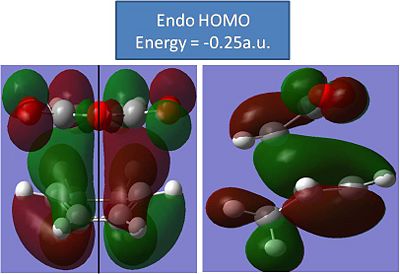
With the optimisations of the molecules complete, the molecular orbitals need to be modelled. The HOMO's of the transition structures should reveal some secondary orbital overlap that will also further proove that the endo transition state is more stable.
Endo:
Exo:
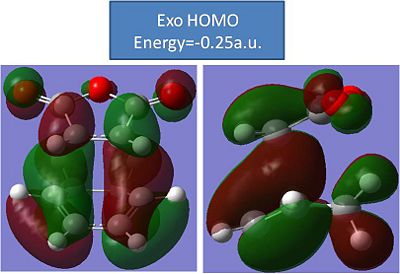
The results of this modelling are disappointing. The HOMO do not reveal any real secondary orbital overlap from the C=O's or the C-O-C's. Both the HOMO's look very similar and have the same number of nodal planes. Both HOMO's have pretty much identical energies(to 2 decimal places)and don't really reveal anything.
From this it can be concluded that for the modelling methods used in this section the main reason for the difference in energy between the transition states is the steric interactions with the hydrogens in the exo ts. Either it can be concluded that there is no secondary orbital overlap in either transition state, or that the computational techiniques used are not powerful enough to predict them. Perhaps a superiour method or basis set would lead to better results.
Errors:
The energy will have an error of ≈ 10 kJ/mol i.e. 0.0038 a.u.
Frequencies are accurate to 0 decimal places. There is also a 10% error on all of them. this can prove to be very large for large frequencies.
bond distances are accurate to ≈ 0.01 Å
bond angles are accurate to ≈ 0.1°
References:
http://www.ch.ic.ac.uk/hunt/teaching/teaching_comp_lab_year3/8a_accuracy.html
