Rep:Mod:MWBINORAGNICIONICLIQUIDS
Week 2 - Ionic Liquids Mini-Project
Introduction
Ionic Liquids are solutions composed entirely of ions which melt below 100ºC, unlike simple inorganic salts such as NaCl which are termed as molten salts as they only melt at high temperatures (such as over 800ºC in this case). A large number of potential anion and cation groups allow for the tuning of unique and desirable physical properties for synthetic applications.[1] Commonly ionic liquids are composed of a bulky organic cations and inorganic anions, due to their low volatility they are a green alternative to traditional organic solvents and have high thermal stabilities due to very stable ion pairs.
Optimisation
[N(CH3)4]+, [P(CH3)4]+ and [S(CH3)3]+ were optimised using the medium level theory 6-31G(d,p) basis set and B3LYP method. The nosymm keyword was used to optimise the cations so that they did not have a fixed geometry and so the global minimum on the potential energy surface could be found if the methyl groups were to rotate. Keywords opt=tight int=ultrafine scf=conver=9 were also used to ensure a tight convergence to the minimum.
| Compound | 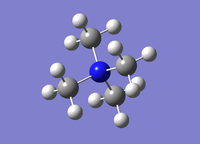 |
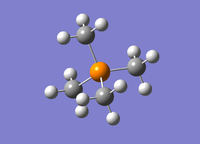 |
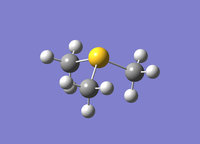 |
| File name | log_88856optnosym | log_88852 | log_88853 |
| File Type | .log | .log | .log |
| Calculation Type | FOPT | FOPT | FOPT |
| Calculation Method | RB3LYP | RB3LYP | RB3LYP |
| Basis Set | 6-31G(d,p) | 6-31G(d,p) | 6-31G(d,p) |
| Charge | 1 | 1 | 1 |
| Spin | Singlet | Singlet | Singlet |
| E(RB3LYP) / a.u. | -214.18127322 | -500.82701172 | -517.68327440 |
| RMS Gradient Norm / a.u. | 0.00000044 | 0.00000074 | 0.00000112 |
| Dipole Moment / Debye | 6.70 | 19.01 | 5.91 |
| Point Group | C1 | C1 | C1 |
| C-X bond length (Å) | 1.51 | 1.82 | 1.82 |
| C-X-C bond angle (°) | 109.5 | 109.5 | 102.7 |
| Job cpu time | 15 minutes 5.9 seconds | 20 minutes 40.0 seconds | 8 minutes 4.2 seconds |
| Link to log file | here | here | here |
It was calculated that the [N(CH3)4]+ C-N bond length is 1.51 Å which matches well with the literature value of 1.49 Å.[2] To get a more exact value matching to literature a larger basis set such as MP2 could be used. The C-N-C bond angle was calculated to be 109.5° which validates the expected sp3 tetrahedral structure of the molecule.
It was calculated that the [P(CH3)4]+ P-N bond length is 1.82 Å which matches well with the literature value of 1.83 Å.[3] The C-P-C angle was also determined to be 109.5° which confirms the molecules tetrahedral structure.
It was calculated that the [S(CH3)3]+ C-S bond length is 1.82 Å which is very close to the literature bond length of 1.81 Å.[4] The C-S-C bond angle was calculated to be 102.7°, this differs quite a lot from the assumed pyramidal bond angle of 107.5° (in NH3). This is due to the contribution of two factors, firstly the sulphur lone-pair in the 3sp3 causing a large repulsion between the the three 2 centre 2 electron sigma bonds, causing the bond to compress, secondly due to the weak overlap of the diffuse 3sp3 orbitals of sulphur with the 2sp3 hybridised on carbon. As sulphur is not as electronegative as nitrogen, it doesn't hold as much as the electron density near itself and as a result the methyl groups are pushed closer together, therefore reducing the bond angle.
| Molecule | Item table |
|---|---|
| [N(CH3)4]+ | Item Value Threshold Converged?
Maximum Force 0.000002 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000017 0.001800 YES
RMS Displacement 0.000006 0.001200 YES
Predicted change in Energy=-2.610693D-11
Optimization completed.
-- Stationary point found.
|
| [P(CH3)4]+ | Item Value Threshold Converged?
Maximum Force 0.000001 0.000015 YES
RMS Force 0.000000 0.000010 YES
Maximum Displacement 0.000048 0.000060 YES
RMS Displacement 0.000013 0.000040 YES
Predicted change in Energy=-9.323328D-11
Optimization completed.
-- Stationary point found.
|
| [S(CH3)3]+ | Item Value Threshold Converged?
Maximum Force 0.000002 0.000015 YES
RMS Force 0.000001 0.000010 YES
Maximum Displacement 0.000055 0.000060 YES
RMS Displacement 0.000019 0.000040 YES
Predicted change in Energy=-1.568213D-10
Optimization completed.
-- Stationary point found.
|
It can be seen that all of the optimisations on the molecules have converged to a stationary point on their respective potential energy surfaces, therefore further frequency analysis will determine whether a minimum has been found.
Frequency Analysis
The frequency analysis was carried out using the 6-31G(d,p) basis set and B3LYP method with keywords: nosymm, opt=tight, int=ultrafine, scf=conver=9.
| Molecule | Low frequencies | IR spectrum | Log file |
|---|---|---|---|
| [N(CH3)4]+ | Low frequencies --- -5.4183 -2.1310 -0.0010 -0.0008 -0.0008 4.0442 Low frequencies --- 183.7687 288.4039 288.9032 |
 |
here |
| [P(CH3)4]+ | Low frequencies --- -2.5571 -0.0012 -0.0010 0.0009 5.1789 7.5929 Low frequencies --- 156.4456 192.0342 192.2771 |
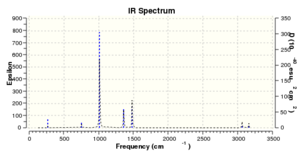 |
here |
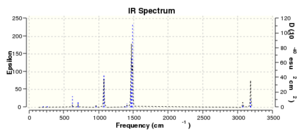
| [S(CH3)3]+ | Low frequencies --- -7.2509 -6.2783 0.0023 0.0025 0.0044 9.6364 Low frequencies --- 162.1102 199.4681 200.0905 |
 |
here |
The low frequency values for the three cations are within the +-20 cm-1 range, therefore indicating that the minimum energy structures have been found on the potential energy surface. There are no negative imaginary frequencies and so this can ensure a transition state structure has not been found.
Population Analysis
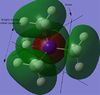
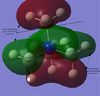
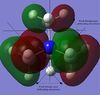
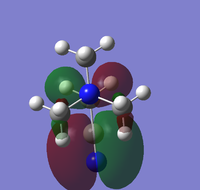
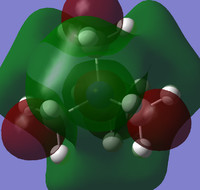
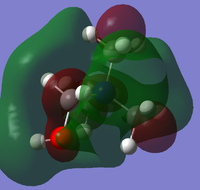
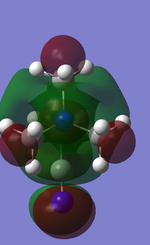
Population analysis was carried out on the previously optimised structures of the three cations with 6-31G basis set, B3LYP method and keywords: pop=full, opt=tight, int=ultrafine and scf=conver=9. Below are 5 MOs of the non-core orbitals of [N(CH3)4]+ showing highly bonding and antibonding orbital interactions.
| Molecule | Log file |
|---|---|
| [N(CH3)4]+ | here |
| [P(CH3)4]+ | here |
| [S(CH3)3]+ | here |
NBO Analysis
The NBOs of the cations were generated through the .log files of the population analysis calculations, these were then tabulated below (charges range from -0.500 to 0.500).
| Charge Distribution of [N(CH3)4]+] | |
|---|---|
| |
| Atom | Charge (e) |
| N | -0.295 |
| C | -0.483 |
| H | 0.269 |
In the NBO charge distribution picture above it can be seen that the carbon atoms bear most of the negative charge, whereas the hydrogen atoms bear all of the positive charge. This is contrasted with the traditional view of the cation with most of the positive charge on the nitrogen atom, even though the nitrogen atom has donated its lone pair to form an extra N-C bond it still retains some of its electron density due to its high electronegativity leading to a tightly bound lone pair and a negative charge (66% still on the N atom as seen by NBO analysis). The inductive effect of the nitrogen atom via the sigma framework of the molecule also depends on the strength of the orbital overlap between the nitrogen an carbon atoms, as both atoms are in the same row of the periodic table we can expect that there will be good overlap between the orbitals. The carbon atoms are negatively charged due to inductive withdrawing effects with the attached hydrogen atoms as the carbon atoms are more electronegative leading to overall positively charge hydrogen atoms. As we can see a more appropriate representation of the cation would be with the positive charge smeared out overall the whole molecule as in [N(CH3)4]+ rather than solely on the central nitrogen atom. As expected the total charge of the molecule adds up to one.
| Charge Distribution of [P(CH3)4]+] | |
|---|---|
| |
| Atom | Charge (e) |
| P | 1.667 |
| C | -1.06 |
| H | 0.298 |
In [P(CH3)4]+ the central P atom is less electronegative than N in the previous molecule, and so holds onto its lone pair less tightly and is able to donate it more freely. The Carbon atoms are more electronegative than the the phosphorous atom and so this leads to a positively charged P atom with negatively charged C atoms surrounding it. In the NBO analysis we can see that 60% of the electron density is pulled towards the sp3 hybridised carbon atom in the P-C bond. This is also due to the fact there is a weaker orbital overlap between the second row carbon atom and third row phosphorous atom (due to mismatch of orbital sizes) and so there is a weaker lone pair donation onto the carbon atom, leading to the large positive charge on the phosphorous atom. The hydrogen atoms bear a positive charge again due to the inductive withdrawing effects of the carbon atoms, and the carbon atoms bear a more negative charge than in N(CH3)4]+ molecule due to these effects. Overall as expected the charges add up to one.
| Charge Distribution of [S(CH3)3]+] | |
|---|---|

| |
| Atom | Charge (e) |
| S | 0.917 |
| C | -0.846 |
| H equitorial | 0.297 |
| H axial | 0.279 |
In [S(CH3)3]+ the carbon atoms bear all of the negative charge due to the inductive withdrawing effects on the adjacent hydrogen atoms due to the greater electronegativity of carbon compared to hydrogen. Sulphur has a lower electronegatvity than nitrogen and so is better at donating its lone pair, but has a similar value to carbon, therefore most of the positive charge is localised on it. This is also due to the fact that there is a weaker overlap between the second row carbon orbitals and the third row sulphur orbitals, leading to a weaker lone pair donation and so more of the positive charge is localised on the sulphur atom. However it can be seen that there are two different positive values for the charge distribution on the hydrogen atoms, the axial (anti-periplanar) hydrogen atoms have a less positive value whilst the equitorial (syn-periplanar) hydrogens have a more positive value. This is due to secondary orbital interactions because of the overlap of the filled σ bond of the sulphur lone pair and σ* orbital of the anti-periplanar C-H bond. Thus donation of electron density into the C-H orbital reduces the positive charge at the H atom and so we can observe the difference in charges at the H atoms as seen above.
The Second Order Perturbation Theory Analysis of Fock Matrix in a NBO Basis below shows the interaction of the sulphur lone pair with the anti-periplanar hydrogens, which yields a value of 2.32 kcal/mol which could be responsible for the difference in charges seen on the hydrogens.
Donor NBO (i) Acceptor NBO (j) kcal/mol a.u. a.u. ====================================================================================== 21. LP ( 1) S 13 /100. BD*( 1) C 1 - H 4 2.32 1.02 0.043 21. LP ( 1) S 13 /103. BD*( 1) C 5 - H 8 2.32 1.02 0.043 21. LP ( 1) S 13 /106. BD*( 1) C 6 - H 10 2.32 1.02 0.043
Orbital contributions to C-X bond
NBO population analysis was done in order to compare and contrast the relative contributions of the C and hetero-atom orbitals to the C-X bond of the three cations.
| Molecule | Orbital contribution outcome |
|---|---|
| [N(CH3)4]+ |
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
4. (1.98452) BD ( 1) C 1 - N 17
( 33.65%) 0.5801* C 1 s( 20.78%)p 3.81( 79.06%)d 0.01( 0.16%)
-0.0003 -0.4552 0.0237 -0.0026 -0.8884
-0.0377 0.0001 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 -0.0352 0.0203
( 66.35%) 0.8146* N 17 s( 25.00%)p 3.00( 74.97%)d 0.00( 0.03%)
0.0000 -0.5000 0.0007 0.0000 0.8658
-0.0001 -0.0001 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 -0.0154 0.0089
|
| [P(CH3)4]+ |
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
4. (1.98030) BD ( 1) C 1 - P 17
( 59.57%) 0.7718* C 1 s( 25.24%)p 2.96( 74.67%)d 0.00( 0.08%)
0.0002 0.5021 0.0171 -0.0020 0.8640
-0.0158 -0.0002 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0251 -0.0145
( 40.43%) 0.6358* P 17 s( 25.00%)p 2.97( 74.15%)d 0.03( 0.85%)
0.0000 0.0001 0.5000 -0.0008 0.0000
0.0000 -0.8611 0.0012 0.0000 0.0001
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0800 -0.0462
|
| [S(CH3)3]+ |
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
4. (1.98631) BD ( 1) C 1 - S 13
( 48.67%) 0.6976* C 1 s( 19.71%)p 4.07( 80.16%)d 0.01( 0.14%)
0.0003 0.4437 0.0140 -0.0033 0.8909
-0.0030 0.0436 0.0056 -0.0762 -0.0098
0.0032 -0.0055 0.0001 0.0316 -0.0183
( 51.33%) 0.7165* S 13 s( 16.95%)p 4.86( 82.42%)d 0.04( 0.63%)
0.0000 0.0001 0.4117 -0.0075 0.0012
0.0000 -0.8977 0.0258 0.0000 -0.0637
-0.0179 0.0000 0.1112 0.0311 0.0161
-0.0281 -0.0040 0.0639 -0.0342
|
We can see from the table above that the nitrogen atom in the N(CH3)4]+ molecule holds 66.35% of the electron density in the C-N bond. The NBO analysis calculations model the electron density of the entire molecule via its constituent atomic orbitals , which is then used to make two centre two electron bonds. Traditionally the nitrogen atom bears the formal positive charge, however we can see that the electrons in the covalent C-N bond are not shared equally as electronegativty comes into play, therefor the nitrogen atom does not bear +1 charge but actually has a negative charge due to its high electronegativity as discussed previously.
In the P(CH3)4]+ molecule only 40.43% of the electron density in the C-P bond is localised on the phosphorous atom, therefore providing a charge of greater than +1 (+1.667) which is due to the the carbon atoms greater electronegativty and inductive effects.
Considering S(CH3)3]+, due to the similar electronegativty of the sulphur and carbon atoms, the sulphur atom has 51.33% of the electron density localised on it in the C-S bond. This leads to an almost equal share of electrons in the covalent bond and a nearly a +1 charge on the sulphur atom (+0.917).
Part 2 Influence of Functional Groups
Optimisation
[N(CH3)3(CH2OH)]+ and [N(CH3)3(CH2CN)]+ were optimised using the medium level theory 6-31G(d,p) basis set and B3LYP method as in the previous section. Keywords used: nosymm, opt=tight, int=ultrafine and scf=conver=9 were also used to ensure a tight convergence to the minimum.
| Compound |  |
 |
| File name | OptimisationNCH33OH631Gdpnosymm1 | OptinisationNCH33CN631Gdptightnosymm1 |
| File Type | .log | .log |
| Calculation Type | FOPT | FOPT |
| Calculation Method | RB3LYP | RB3LYP |
| Basis Set | 6-31G(d,p) | 6-31G(d,p) |
| Charge | 1 | 1 |
| Spin | Singlet | Singlet |
| E(RB3LYP) / a.u. | -289.39470749 | -306.39376169 |
| RMS Gradient Norm / a.u. | 0.00000063 | 0.00000052 |
| Dipole Moment / Debye | 5.28 | 9.31 |
| Point Group | C1 | C1 |
| Job cpu time | 33 minutes 21.5 seconds | 28 minutes 30.0 seconds |
| Link to log file | here | here |
| Molecule | Item table |
|---|---|
| [N(CH3)3(CH2OH)]+ | Item Value Threshold Converged?
Maximum Force 0.000001 0.000015 YES
RMS Force 0.000000 0.000010 YES
Maximum Displacement 0.000016 0.000060 YES
RMS Displacement 0.000004 0.000040 YES
Predicted change in Energy=-1.768701D-11
Optimization completed.
-- Stationary point found.
|
| [N(CH3)3(CH2CN)]+ | Item Value Threshold Converged?
Maximum Force 0.000001 0.000015 YES
RMS Force 0.000000 0.000010 YES
Maximum Displacement 0.000025 0.000060 YES
RMS Displacement 0.000007 0.000040 YES
Predicted change in Energy=-1.748765D-11
Optimization completed.
-- Stationary point found.
|
It can be seen that all of the optimisations on the molecules have converged to a stationary point on their respective potential energy surfaces, therefore further frequency analysis will determine whether a minimum has been found.
Frequency Analysis
The frequency analysis was carried out using the 6-31G(d,p) basis set and B3LYP method with keywords: nosymm, opt=tight, int=ultrafine, scf=conver=9.
| Molecule | Low frequencies | IR spectrum | Log file |
|---|---|---|---|
| [N(CH3)3(CH2OH)]+ | Low frequencies --- -7.4589 -4.3208 0.0006 0.0007 0.0011 4.4674 Low frequencies --- 131.4307 214.2624 255.4547 |
 |
here |
| [N(CH3)3(CH2CN)]+ | Low frequencies --- -4.3090 -3.5018 -0.0012 -0.0010 -0.0010 5.3613 Low frequencies --- 91.6075 153.8468 211.3408 |
 |
here |
The low frequency values for the two cations are within the +-20 cm-1 range, therefore indicating that the minimum energy structures have been found on the potential energy surface. There are no negative imaginary frequencies and so this can ensure a transition state structure has not been found.
Population Analysis
Population analysis calculations was carried out using the 6-31G(d,p) basis set and B3LYP method with keywords: pop=full, nosymm, opt=tight, int=ultrafine, scf=conver=9 on the previously optimised molecules.
| Molecule | Log file |
|---|---|
| [N(CH3)3(CH2OH]+ | here |
| [N(CH3)3(CH2CN)]+ | here |
NBO Analysis
The NBOs of the cations were generated through the .log files of the population analysis calculations, these were then tabulated below (charges range from -0.500 to 0.500).
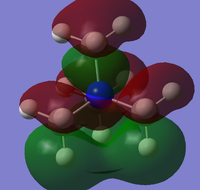
The OH ligand is an electron donating group, and so has had a marked change on the overall charge distribution of the molecule compared with the [N(CH3)4]+ molecule. The first thing to note is that the there is now a more negative charge on the central nitrogen atom than in [N(CH3)4]+ due to the delocalisation of electron density between the N-C-O fragment, allowing the hydroxy oxygen atom to donate electron density onto the nitrogen atom, which can be seen through the molecular orbital diagram below.

The second point to note is that all of the carbon atoms have a similar values of negative charge on them compared to the [N(CH3)4]+ molecule except for the carbon atom adjacent to the hydroxy group which bears a slightly positive charge of +0.088. This is due to the inductive withdrawal effects of the oxygen atom on the carbon atom due to differences in electronegativity.
Lastly we can see that hydrogen atoms 8 and 9 which are adjacent to the hydroxy group have a slightly less positive charge than the other methyl hydrogens in the molecule. This is due to electron density from the oxygen lone pair being donated onto the two hydrogen atoms, which can be seen through the Second Order Perturbation Theory Analysis of Fock Matrix in a NBO Basis below.
Donor NBO (i) Acceptor NBO (j) kcal/mol a.u. a.u. ====================================================================================== 25. LP ( 2) O 17 /140. BD*( 1) C 5 - N 16 18.96 0.51 0.088
Donor NBO (i) Acceptor NBO (j) kcal/mol a.u. a.u. ====================================================================================== 24. LP ( 1) O 17 /138. BD*( 1) C 5 - H 8 1.21 1.04 0.032 24. LP ( 1) O 17 /139. BD*( 1) C 5 - H 9 3.97 1.02 0.057 25. LP ( 2) O 17 /138. BD*( 1) C 5 - H 8 2.97 0.77 0.043 25. LP ( 2) O 17 /139. BD*( 1) C 5 - H 9 0.83 0.75 0.023
It can be seen that the oxygen atom donates a larger amount of electron density from its lone pair onto hydrogen atom 9 therefore as we expect it has a lower positive charge than hydrogen atom 8. Second order perturbation analysis was also done on the donation of the oxygen lone pair on to the central nitrogen atom which has a value of 18.96 kcal/mol which is quite large and indicates a significant degree of delocalisation of the oxygen lone pair via the N-C-O fragment as mentioned above.
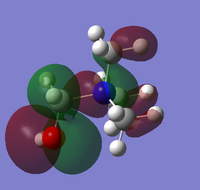
The CN ligand is an electron withdrawing ligand, and so has had a marked change on the overall charge distribution of the molecule compared with the [N(CH3)4]+ molecule. The central nitrogen atom has a similar value of negative charge with respect to the nitrogen atom in the [N(CH3)4]+, however the carbon atom adjacent to the central nitrogen (carbon atom 6) has significantly less electron density than the other methyl carbon atoms due to the electron withdrawing pi orbital inductive effects of the nitrile ligand, which is less significant than the hydroxy groups inductive effect as this propagates via sigma orbitals.
The nitrile group carbon atom has a positive charge due to the inductive withdrawal effects of the neighbouring nitrogen atom which has a greater value of electronegativity causing electron density to pulled towards the nitrogen atom.
The hydrogen atoms 11 and 12 also have a larger positive charge than the other methyl hydrogen due to the electron withdrawing effects of the nitrile group.
HOMO and LUMO comparison of [N(CH3)4]+, [N(CH3)3(CH2OH)]+ and [N(CH3)3(CH2CN)]+
It can be seen that the introduction of the OH and CN ligands have drastically changed the shapes of the molecular orbitals. One of the main differences is that in the HOMO of [N(CH3)3(CH2OH)]+ molecule there is no longer a bonding interaction between the methyl hydrogens of the three carbon atoms, the introduction of the hydroxy group has reduced the delocalisation of the MO due to the the electronegative withdrawal effects of the oxygen atom. Antibonding interactions are also seen between the lone pair of the oxygen and the adjacent CH2 group which increases the overall antibonding character of the MO and so it has a higher energy compared to the [N(CH3)4]+ HOMO.
In the LUMO of the [N(CH3)4]+ molecule there is a large amount of delocalisation of charge, however when the OH group is introduced the sigma bonding framework of the molecule is disrupted via electron donation of the oxygen atom lone pair into the N-C-O fragment of the molecule as seen in the NBO charge analysis above. This reduction in symmetry causes the LUMO to have a higher antibonding character and energy than in the tetramethylammonium cation. This destabilisation of the molecule therefore infers that it will be a weaker acceptor and so will not interact with the ion pair anion as strongly, leading to a lower thermal stability and melting point. However the effect of hydrogen bonding due to the hydroxy group may need to be taken into account.
We can see in the HOMO of [N(CH3)3(CH2CN)]+ that a large proportion of the electron density has been pulled away from the central nitrogen atom and methyl group fragments and almost no interactions are present here. However most of the electron density is situated on the nitrile group due to its electron withdrawing effects via pi bonding framework, and antibonding interactions can be seen between the nitrile group and the methyl hydrogen atoms which raise the energy of the HOMO and its antibonding character with respect to the tetramethylammonium cation.
Considering the LUMO of [N(CH3)3(CH2CN)]+ we can see it lies deeper in energy than the corresponding [N(CH3)4]+ cation. This is due to the decreased antibonding interactions of the p orbitals of the methyl groups with the diffuse electron density at the centre of the molecule via the reduction of the orbital size by the inductive withdrawal effect of the nitrile group. Even though antibonding interactions occur between the pi bond of the nitrile group and the adjacent CH2 orbital, overall the interactions are more stabilising and so the LUMO is lower in energy with respect to the LUMO of the tetramethylammonium cation. Therefore we can expect that the cation will act as a better acceptor and so will interact with an anion more strongly, leading to a higher thermal stability and melting point.
| Cation | HOMO-LUMO Energy Gap (a.u.) | HOMO-LUMO Energy Gap (kJ/mol) |
|---|---|---|
| [N(CH3)4]+ | 0.44632 | 1171.8 |
| [N(CH3)3(CH2OH]+ | 0.36303 | 953.1 |
| [N(CH3)3(CH2CN]+ | 0.31865 | 836.6 |
It can be seen that there is a reduction in the HOMO-LUMO gap of the functionalised cations compared to [N(CH3)4]+. The HOMO-LUMO gap is indicative of the stability of the cations, and a smaller energy gap shows that both of the functionalised cations will lead to more stable ion-pairs, as the addition of electron density to the cation is less energetically demanding, and so will be more suitable ionic liquids.
Conclusion
The three onoium cations [N(CH3)4]+, [P(CH3)4]+ and [S(CH3)3]+ were initially investigated via computational methods and their physical properties and charge distributions were rationalised via NBO population analysis and second order perturbation theory. Subsequently different functional groups were placed on the [N(CH3)4]+ cation and they were analysed through the same methods previously described in order to compare and contrast the affect of different ligands on the shapes and energies of the resulting molecular orbitals and so on the properties of the ionic liquids, showing the potential applications of the designer solvents.
Further Study
Research into the effects of hydrogen bonding due to the hydroxy group in the [N(CH3)3(CH2OH)]+ molecule could be done in order to determine how much this phenomenon effects the shapes of the MOs and so the molecules HOMO-LUMO energy gap. The cations could also be modeled in gaussian coordinating with an anion to show how this also effects the HOMO-LUMO energy gap of the molecules and so their chemical and physical properties as ionic liquids.
References
- ↑ Hermann Weingartner, Understanding Ionic Liquids at the Molecular Level:Facts, Problems, and Controversies, Angewandte Chemie,2008, 47 (4),654
- ↑ E. A. Trush, O. V. Shishkin, V. A. Trush, I. S. Konovalovab and T. Y. Sliva, Tetramethylammonium dimethyl (phenylsulfonylamido)phosphate(1−), Acta Crystallographica, 2012, 68(2), 273
- ↑ Andreas Kornath, F. Neumann and H. Oberhammer, Tetramethylphosphonium Fluoride:“Naked” Fluoride and Phosphorane, Inorganic Chemistry, 2003 42 (9), 2894
- ↑ Pradip Ghosh and Animesh Chakravorty, On alkyl sulfonium salts of triiodomercury(II) and structure of the trimethyl salt, Indian Journal of Chemistry, 2013, 52A, 1247