Physical Chemistry Computational Laboratory

The Cope rearrangement

Introduction

The cope rearrangement is a fundamental ractions in organic chemistry, its discovery has led to enormous step forwards in the structural and mechanistic understanding of pericyclic rearrangements. Formally it consists of a [3,3]-sigmatropic reaction of a 1,5-hexadiene moiety to its degenerate isomer. Since 1940 when Cope and Hardy found that heating of ethyl-1-methylpropenyl-allylcyanoacetate gives an isomeric substance that indicated an allyl group shift^[1] a large amount of work has been done in the attempt to better understand the mechanistic route underlying the rearrangement. Most of the investigation carried out had the purpose of determining whether the rearrangement proceeds via a aromatic transition state or a biradical intermediate. This work provided the basis for the "Cope family".^[2] However the Cope rearrangement does not only have a theoretical importance, in fact it is widely used in the synthesis of natural products and it is of great importance in biological processes.^[3] The importance of biradical intermediates in the "Cope Family" rearrangements has a key role in the development of anti-tumor drugs.

Well established concepts of physical organic chemistry, such as the Woodward-Hoffman's rules of orbitals symmetry conservation and Fukui's frontier molecular orbital theory make up the framework upon which pericyclic reaction have been theoretically understood providing the idea that these reactions occur by concerted mechanism.^[2] Although the Cope reaction was immediately recognised to be concerted there was still the open question of what the mechanism for this heat activated reaction was. The geometry for this rearrangement can go either through a chair or a boat conformation TS but also through a aromatic or biradical transition state. Although the mechanism involving a biradical is of great utility it happens to a much smaller extent that the aromatic type TS, therefore the present work will focus on the relative energy of the two possible chair and boat TS for the rearrangement. However the stable conformations of [1,5]-hexadiene are first investigated.

Method

In the quest for the possible stable conformations of [1,5]-hexadiene quantum mechanical calculations have been used. The methods adopted were in general Hartree-Fock theory and Density Functional Theory.

Hartree-Fock

Hartree-Fock consist in a approximate method for the determination of the ground state wavefunction and ground state energy of a quantum many-body system. In general Hartree-Fock method describes non-interacting electrons under the influence of a mean field consisting of the classical Coulomb potential and a non-local exchange potential. Introduction of correlation in the HF-method brings great improvements to the accuracy of the method but also an enormous increase in its computational demand. For this reason HF-correlated methods are only feasible for small systems and in order to obtain an accurate picture of the energy profile of the molecule DFT methods need to be introduced.

Density Functional Theory

The need of DFT is necessary to compute accurate energies and densities for systems with a large number of electrons. In fact in order to compute the 3N dimensional wavefunction of a system of N electrons is computationally unaffordable. However it turns out that knowledge of the two-particle probability density (the probability of finding an electron at the position r₁ and an electron at the position r₂) is sufficient. It can be found by a derivation that goes behind the scopes of this report that the diagonal elements of the first and second order density matrices P1 and P2 completely determine the total energy and therefore a 3N-dimensional problem can be reduced to a 6-dimensional problem. Approaches based on the minimization of E(P1,P2) have the problem of ensuring that the density matrices have to be constructed by unsymmetrical wavefunctions. Imposing this constraint is not trivial and it is an unsolved problem yet. The idea underpinning DFT is that P2 is not needed to find E, in fact P1 is sufficient.Honeburg-Kohn in 1964 proved two theorems. The first one states that: "The electron density determines the external potential within an additive constant", from this it follows that the electron density uniquely defines the Hamiltonian operator. This concept was generalized by Levy in 1979 to degenerate systems. The second theorem is the DFT-variation principle and state that: "For any positive definite trial density, ρ_t, such that ʃρ_t(r)dr=N then E[ρ_t] is equal or greater than E₀". This theorem restricts density functional theory to the ground state, although there are extension that allow the study of excited state. The two theorems lead to the the fundamental statement of density functional theory :

δ[E[ρ]-μʃ(ρ(r)dr-N)]=0

The ground state energy and density correspond to the minimum of some functional E[ρ] subject to the constraint that the density contains the correct number of electrons. μ is the electronic chemical potential. The general idea is that there is a universal function E[ρ] which if known could be inserted into the above equation and minimized to obtain the exact ground state energy and density.^[4]

Example of Input file

#p opt freq hf/3-21g geom=connectivity int=ultrafine scf=conver=9
blank line)
Title
(blank line)
charge spin
(blank line)
coordinates
(blank line)
connectivity
(blank line)

the #p instead of a simple # calls for an extended printout, specifically it switches on the printing of the SCF convergence
The "opt freq" command requests structural optimization and frequency analysis
The key word hf/3-21g refers to the method hf (Hartee-Fock) and 3-21g is the basis set of choice. 3-21G is a split-valence basis set. The idea behind this type of basis sets is that inner electrons are not as important as the valence electrons in determining electronic properties, therefore these will be described by a single Slater Orbital. 3-21G means that 3 gaussian functions are summed to describe the inner shell orbital, 2 and 1 are the numbers of gaussian functions used to describe respectively the first and the second Slater Type Orbital for the valence electrons.
geom=connectivity tells the software to read the connectivity of the molecule referring to the last lines of code where the connectivity of each atom is described.
int=ultrafine scf=conver=11 imposes stricter convergence criteria than by default
under the first blank line is the title and after the second overall charge and spin are specified. A list of atoms and corresponding coordinates follows.

For some calculations b3lyp/3-21g were used in order to achieve more accurate results, B3lyp stands for Becke, 3-parameter,Lee-Yang-Parr. This is a hybrid functional method that includes a mixture of Hartree-Fock and DFT exchange correlations. The general Becke three parameter Hybrid functionals have the following form for the exact energy exchange correlation approximation: E_XC=a₀*E_X^Slater+(1-a₀)E_X^HF+a_xΔE_X^Becke+E_C^VWN+a_c*ΔE_C^non-local where a₀,a_x and a_c are semiempirical coefficients determined by Becke fitting to the G1 molecule set.^[5] HBRLYP is a "flavor" of this hybrid functional, it uses the non-local correlation provided by the LYP ^[6]expression and VWN functional III for local correlation (instead of V). The correlation functional used is a_CE_C^LYP+(1-a_C)E_C^VWN. Since LYP includes boh local correlation functional, the VWN is used to provide the excess local correlation required since LYP contain a local term equivalent to VWN.

Optimizations

As it was briefly mentioned above an investigation of the possible stable conformations of [1,5]-hexadiene was carried out. Two main classes of starting conformations for the minimization of the structures can be identified with respect to the [3,4]-carbon bond: one with the allyl groups anti and the other with the allyl groups gauche to each other. The two families of possible initial conformations are formed by a number of different possible conformations. As it will be discussed later the main difference between the two families of conformers is that when undergoing the cope rearrangement the first goes through a chair like TS and the other through a boat like TS. The optimization routes first for the anti and then for the gauche conformations are presented below. The process of optimization has led to the identification of some transitions states as the initial configurations were so far from a stable conformation that they converged to a metastable transitions state. Whenever one of these metastable conformations are met an animated picture of the identified negative vibration is displayed. This vibration represents the atomic displacements necessary to escape the metastable state. These TS are then re-optimized after displacing the atoms in the direction of the vibration displacement vector. Internal Reaction Cooordinate analysis shows the evolution of a transition state along its negative vibration down to an optimized state. This topic will be further investigate later.

Anti Conformations

A number of anti-like starting conformations were optimized in order to find the lowest energy conformation. The starting conformations are labeled as anti-s(number) where s stands for starting. Energy and Point groups are reported for the optimized structure. The nomenclature for these is in accordance with the structures reported in Appendix 1. The level of theory for these optimization was Hartree-Fock with 3-21G basis set.

	Transition State vibration= -138 cm^-1	anti-2 [Ci] E = -231.69254 a.u.
anti-s1
	Transition state vibration= -96 cm^-1	anti-1 [C2] E = -231.69260 a.u.

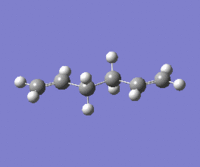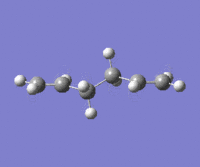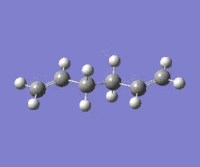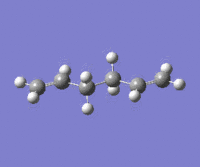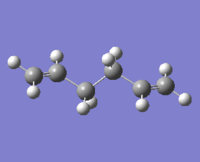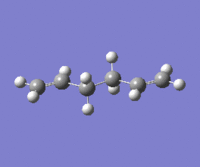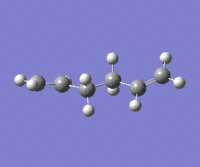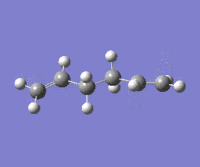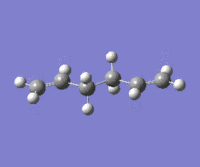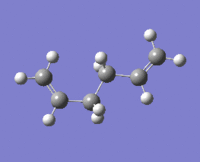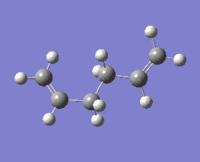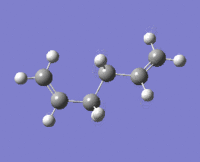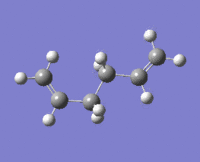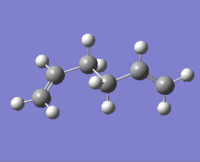The lowest energy conformation anti-2 [Ci] is found from optimization of the TS vibration at -138 cm^-1 of the optimized anti-s1 configuration.

Gauche Conformations

A large number of stable conformations can be calculated for the gauche like conformers. As above the structures are labeled according to the nomenclature of Appendix 1. The nomenclature for the starting conformations is analogous to the one used for the anti: gauche-s[number] where s stands for starting. The level of theory used for the optimizations was Hartree-Fock with 3-21G basis set.

	Transition State Vibration= -116cm^-1	Transition State Vibration=- 155cm^-1	gauche-3 E = -231.69266 a.u. [C1]
gauche-s1	Transition State Vibration= -194cm^-1	gauche-2 [C2] E = -231.69167
	Transition State Vibration= -229cm^-1	gauche-4 [C2] E = -231.69153 a.u.

gauche-s2		gauche-1 [C2] E = -231.68772 a.u.
gauche-s3		gauche-5 [C1] E = -231.68962 a.u.
gauche-s4		gauche-1 [C2] E = -231.68772 a.u.
gauche-s4		gauche-4 [C2] E = -231.69153 a.u.
gauche-s5		gauche-3 [C1] E = -231.69266 a.u.

All the conformations reported in Appendix 1 were obtained with the exception of gauche-6. The lowest conformation found was gauche-3 [C1].

DFT investigation of [C_i]anti-1 lowest energy conformer

Optimization

As mentioned above the [C_i]anti-1 conformer was found to be the lowest in energy anti-like conformer. After the first optimization by Hartree-Fock/3-21G a further optimization by density functional theory b3lyp/6-31G was carried out. Although the energy obtained by the two different methods cannot be compared their structures are comparable. Captions of the optimized structures are reported below:

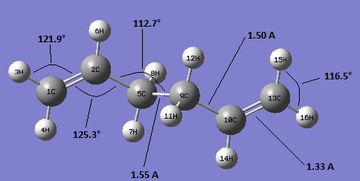
Some of the geometrical parameters are shown here. The angles and bond lengths are identical for the RHS and the LHS with respect to the centre of inversion on the 5C-9C bond. As it can be noted by inspection of the figures bond angles are within 1.3° from each other and bond lengths within 0.01 A. The differences in bond lengths are within the error of 0.01 A. Likewise the difference in bond angles being maximum 1.4° can be regarded not as a significant difference. However one significant difference can be found in the dihedral angles 5C-9C-10C-13C that are 114.6° for HF/3-21G and 118.6° for B3lyp/6-31g*. The 2C-5C-9C-10C dihedral angles are 180° for both structures (if this was not the case then it would not be possible to have point group Ci).

Thermochemistry

Under the thermochemistry section of the output file for the Vibrational Analysis done at the b3lyp/6-31g* level of theory estimates for the total energy of the molecule can be found. The calculated values are reported below:

Sum of electronic and zero-point Energies   = E₀ + ZPE_corr =                         -234.46922 
Sum of electronic and thermal Energies      = E₀ + E_vib + E_rot + E_trans =              -234.46187
Sum of electronic and thermal Enthalpies    = E₀ + H_corr =                           -234.46093
Sum of electronic and thermal Free Energies = E₀ + G_corr =                           -234.50081

where E₀ is the total electronic energy^[7] The first of these parameters is the potential energy at 0K including the zero-point vibrational energy, the second is the energy at standard conditions which includes contributions from the translational, rotational and vibrational energy modes. The third term contains an correction for RT (H = E + RT)which is important when looking at dissociation reactions. The last relation includes entropic contributions of the free energy (G = H - TS). From the Vibrational Analysis done at the hf/3-21g level of theory the following energies were calculated:

Sum of electronic and zero-point Energies   = E₀ + ZPE_corr =                         -231.539540 
Sum of electronic and thermal Energies      = E₀ + E_vib + E_rot + E_trans =              -231.532566
Sum of electronic and thermal Enthalpies    = E₀ + H_corr =                           -231.531622
Sum of electronic and thermal Free Energies = E₀ + G_corr =                           -231.570914

The same analysis was carried at 0 K at b3lyp/6-31g* level of theory using the Freq=ReadIsotopes key word. This function allows the used to determine any Temperature, Pressure and Isotopic mass. Due to the fact that 0K is unachievable a temperature of 0.00001 K was used for the analysis. The electronic enrgies obtained were:

Sum of electronic and zero-point Energies   = E₀ + ZPE_corr =                         -234.46878 
Sum of electronic and thermal Energies      = E₀ + E_vib + E_rot + E_trans =              -234.46878
Sum of electronic and thermal Enthalpies    = E₀ + H_corr =                           -234.46878
Sum of electronic and thermal Free Energies = E₀ + G_corr =                           -234.46878

As it could be expected all values are identical as the molecule is at 0 kelvin.

Optimizing the "Chair" and "Boat" Transition Structures

As it was briefly mentioned in the introduction the main route for the Cope concerted rearrangement goes through a aromatic "chair" like or a "boat" like transition state. The fact that the reaction can go through more than one possible TS was first suggested by the fact that the rearrangement of substituted molecules would give a number of isomers. Here the two transition states are investigated by three different methods:

by computing the force constant at the beginning of the calculation
by using the redundant coordinate method
by using the QST2 method

The first two were used to identify the chair like transition state while the QST2 method was used to identify the "boat" like transition state. The intrinsic reaction coordinate was also run for the obtained Transition states.

"Chair" Transition State optimization

Optimization of the allyl fragment

An allyl fragment was built in gaussview and optimized at the HF/3-21G level of theory.

Two allyl fragments were then copied in the same MolGroup and they were positioned at 2.2 A apart from each other in a reasonable transition state arrangement which resembles a chair conformation. Since both the the force matrix based optimization and the redundant coordinate method yield the same results before showing them the underlying principles for these two optimization are discussed.

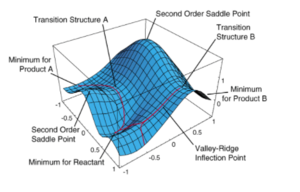
In the diagram above a typical Potential Energy Surface (PES) can be observed.On a PES three types of stationary points can be observed: a minimum, a first and a second order saddle points. Vibrations are the second derivative of the PES, when we are at a stationary point depending on whether the second derivative is greater or less than zero respectively a minimum or a maximum(saddle point) are observed. In this discussion secondary saddle points have no chemical significance as we are looking at a static picture of the molecule: atoms move infinitely slowly and therefore along the IRC. In order to identify a TS a stationary point with negative second derivative has to be identified. To do so the force constant matrix (Hessian) for the molecule can be computed in the first step of the optimization and then updated as the optimization proceeds. However this only works if the point on the PES defined by the guessed structure is in the vicinity of a transition state. Alternatively a TS structure can be determined by freezing some reaction coordinates. This allow to optimized the molecule around a guessed transition structure and then once the molecule is relaxed the coordinates can be unfrozen and the optimization towards a TS can be performed. This is much less time consuming than the force matrix constant method, especially when determination of the Hessian matrix is expensive. The starting point for the transitions state optimization and the result obtained by the Transtion State optimization methods described above are shown here:

The identified negative vibration of the transition state is asymmetric and corresponds to the formation of C-C bonds. It must be noted that the amplitude of the oscillations are exaggerated for clarity purposes.

"Chair" Transition State IRC

The IRC command in the Gaussian environment requests that a reaction path is followed by integrating the internal reaction coordinate^[9]. The initial geometry for this reaction path is that of a transition state and the path can be followed in either directions from that saddle point. The forward direction is defined as the direction in which the transition vector is pointing when the largest component of the transition vector is positive. The evolution of the "chair" like transition state for the Cope rearrangement was investigated by IRC. As in this case the reaction coordinate is symmetrical the IRC was computed only in the forward direction. An example of command line for the IRC calcualtion is the following:

#p irc=(forward,maxpoints=50,calcfc) hf/3-21g geom=connectivity

While everything is analogous to what described above in the Example of Input File the irc command has the following characteristics:

forward is the direction in which the IRC is calculated
maxpoints=50 is the maximum number of points that the program is allowed to calculate to reach convergence
calcfc tells Gaussian to calculate the Hessian once before running the IRC. However this keyword can be replaced with calcall which tells Gaussian to recalculate the Hessian at every reiteration.

In order to obtain the lowest minimum a number of things can be done, either the number of points can be increased or the Hessian can be recalculated at every reiteration. It is also possible to calculate the IRC twice, the second time starting from the structure obtained with the first IRC. Another possibility and also a more time consuming and computationally expensive one is to use all of the options together. This gives the best possible result.

Here all the possibilities described above were attempted in order to find to which conformer the TS leads. Ideally this should be the lowest energy conformation, however the possibility of finding a local minimum has to be taken into account.

The first attempt made was to increase the default 6 steps to 50. The force matrix was set to be calculated once at the beginning of the precedure. The obtained IRC graph and the first derivative of the PES are are shown below

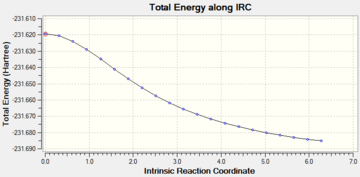
Although the maximum number of steps was set to 50, convergence was reached after 21 reiterations. This was confermed by trying the calculation using an maximum number of 200 steps: convergence was achieved again after 21 reiterations. In order to confirm whether or not the lowest minimum had been reached a second calculations starting from the caclulated minimum was carried out.

As it can indeed be observed a minimum had not been reached, in fact after a further 45 reiterations a lower minimum was found. The total energy for the minimum thus found was E = -231.69140 a.u. Athough this energy is close top the one of the gauche-4 structure in Appendix 1, it does not correspond to any of the lowest energy conformers calculated before, this means that a minimum has not been reached yet. The structure thus obtained is in the gauche configuration.

In order to reach the lowest energy minimum another attempt was carried out. A maximum number of 50 steps was set but the Hessian was set to be recalculated at each reiteration. The IRC converged in 47 steps and a minimum with energy E=-231.69166 a.u. This structure corresponds to the gauche-2 structure of Appendix 1.

Another attempt in the order to find the lowest energy configuration gauche-3 of Appendix 1 was carried out. This time the calculation started from the first optimized structure, as for the two step routine. However the number of possible steps was set to 200 and the Hessian was calculated at every reiteration. After 58 reiterations the overall energy was again E = -231.69166 a.u. .

Starting from this structure one last attempt was carried out, with the same settings. However the IRC conerged after 2 steps confirming that the lowest energy configuration that can be reached by IRC of the "chair like" transition state.

"Boat" Transition State optimization

The "boat" like transition state is another possible conformation through which the Cope rearrangement can proceed. Here it is shown how a transition state cab be found by QST2 method. The method consists in specifying reactants and products so that the software tries to calculate a transitions state between the two. The boat transition state was calculated starting from the [C_i] anti-2 structure optimized above at DFT level of theory. A diagram of the reactant, Transition State and Product is shown below. As it can be noted the calculation has not converged to a "boat" like TS, in fact gaussian would only translate the two fragments but not rotate them.

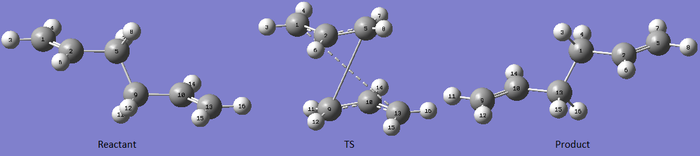
In order to obtained the wanted TS the reactant and product conformations were modified to a Gauche like structure. Doing this the two fragments are in the correct orientation to form a "boat" transition state. The diagram below shows the modified reactants and products and also the converged transition state.

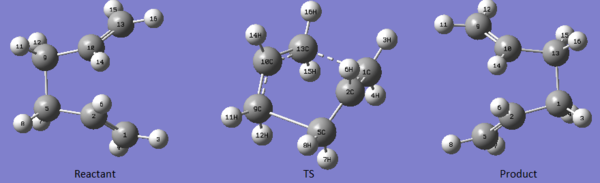
Particular care was given to the numbering of reactants and products, in fact it has to be such that the TS found is the one for a Cope rearrangement.

"Boat" Transition State IRC

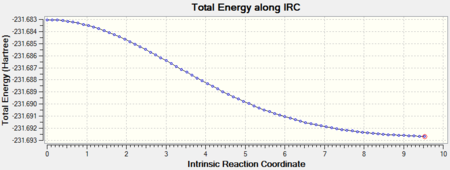
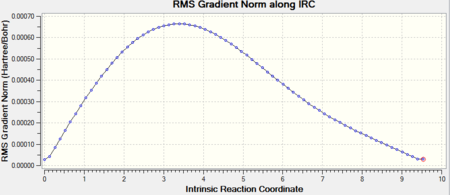
An IRC calculation was carried out for the "boat" like transition state in the same manner as done for the "chair" like TS. For the "boat" TS a IRC a maximum of 250 steps and calculation of the Hessian at every reiteration were set. After 47 reiterations a first minimum with energy E = -231.68303 a.u. was found. However this minimum does not correspond to any of the low energy configurations calculated above.

The same calculation was carried out starting from the structure yielded by the calculation above. A structure with the lowest energy configuration gauche-3 was obtained. For the convergence to be met 74 reiterations were necessary and the energy for the structure was E = -231.69266. The IRC and the first derivative for the PES are shown below:

Transition States Optimization at DFT level of Theory

Optimization for the "boat" and "chair" like calculated transition states was carried out at the b3lyp/6-31g* level of theory. The optimization was carried out on the already optimized TS structures obtained as described above at the HF/3-21g level of theory. The structures for the optimized TS at both levels of theory are shown in in the figures below.

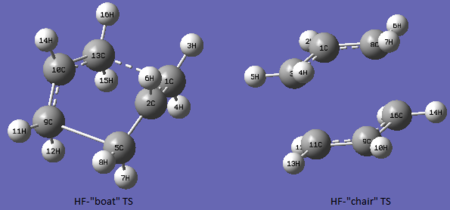
By inspection of the figures it can be noted that the geometry of the transition states are analogous.

The energies for the transitions states and the activation energies with respect to the [C_i]anti-2 conformer energy are listed in the tables below. Electronic energies are reported in Hartrees while the activation energies are reported in kJ/mol. (1a.u. = 2625.49962 kJ/mol)

Electronic energies
	HF/3-21G			B3LYP/6-31G*
Species	Electronic Energy	Sum of Electronic and Zero Point Energy	Sum Of electronic and thermal energies	Electronic Energy	Sum of Electronic and Zero Point Energy	Sum Of electronic and thermal energies
Boat	-231.60280	-231.45093	-231.44530	-234.54308	-234.40235	-234.39601
Chair	-231.61932	-231.46670	-231.46134	-234.55693	-234.41491	-234.40898
[Ci]Anti-2	-231.69254	-231.53954	-231.53257	-234.61171	-234.46922	-234.46187

Activation Energies
	HF/3-21G			B3LYP/6-31G*
Species	Ea Electronic Energy	Ea Sum of Electronic and Zero Point Energy	Ea Sum Of electronic and thermal energies	Ea Electronic Energy	Ea Sum of Electronic and Zero Point Energy	Ea Sum Of electronic and thermal energies
Boat	236	233	229	180	176	173
Chair	192	191	187	144	143	139

As it can be inferred by the calculations above while the difference in activation energy between "Chair" and "Boat" are about 40kJ/mol for both levels of theory, their magnitudes are considerably different for the two. In fact activation energies are about 60kJ larger for HF/3-21G than for DFT/6-31G*. This is a considerable difference in energy between the the two methods. The experimental activation energies are 184±8 kJ/mol for the boat conformations and 140±2 kJ/mol for the chair. These values are in very good agreement with the calculated values by DFT b3lyp/6-31g. The calculated values for boat and chair are respectively 176kJ/mol and 143 kJ/mol. The negative vibrations for the transition states calculated by DFT calculations are shown below.

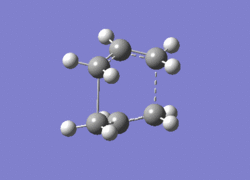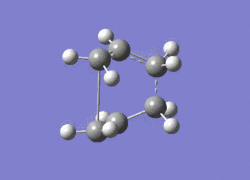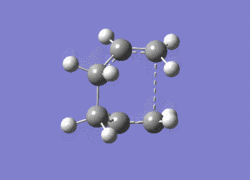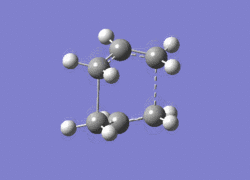Tautomerism of the Transition State

Although it was generally agreed that the Cope rearrangement goes though a cyclic transition state in the 70s-80s the possibility for the involvment of a stepwise reaction involving a symmetrical intermediate or two allyl radicals was investigated. The energies for the different resonance forms of the cyclic transition state were calculated and found to be 8.5 and 26.2 kCal/mol for the symmetrical intermediate radical (SR) and the allyl radical respectively (AR). A energy diagrams with the relative energies is shown below.

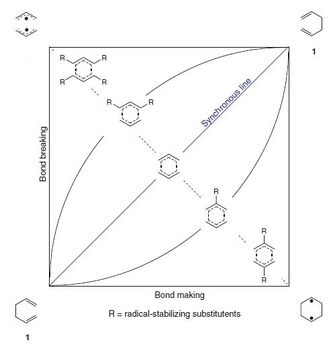While the AR was too high in energy to be a possible intermediate, the calculations conducted suggested that the SR was not so inaccesible. With the purpose of explaining to which extent each tatutomer is actually realized in the transition state O'Ferral-Jencks suggested a plot to explain the TS substituent dependency of the cope reaction as a degree of the ratio of bond breaking and bond making. Doering^[10] conceptualized these finding proposing a Chamaleonic and a Centauric model. Twotype of carbon positions were identified: the nodal positions(C2 and C5) and the active positions(C1,C3,C4 and C6).

The chamaleonic model of substituted rearrangements suggests that only of the three proposed reactions can be embodied at the TS.
The centauric model suggests instead that the TS could have a "multiple-identity" i.e. it could be in a mixed state.

Doering found that the centauric model would be a better model to describe the calculated energies for the systems.

References

↑ Cope AC, Hardy EM. The introduction of substituted vinyl groups—a rearrangement involving the migration of an allyl group in a three-carbon system. J Am Chem Soc 1940, 62:441–444. doi: 10.1021/ja01859a055.
↑ ^2.0 ^2.1 ^2.2 ^2.3 Graulich Nicole. The Cope rearrangement—the first born of a great family. WIREs Comput Mol Sci 2011, 1: 172-190. doi: 10.1002/wcms.17
↑ Pindur U, Schneider GH. Pericyclic key reactions in biological systems and biomimetic syntheses. Chem Soc Rev 1994, 23:409–415. doi: 10.1039/ CS9942300409.
↑ An introduction to Density Functional Theory, N.M. Harrison 2003, in Computational Materials Science, NATO Science Series III, Ed. Catlow and Kotomin, 187, IOS Press
↑ Becke,A J. Chem. Phys. 98, 5648 (1993) doi:10.1063/1.464913
↑ Chengteh Lee, Weitao Yang, and Robert G. Parr, Phys. Rev. B,37,785–789,(1988)
↑ http://www.gaussian.com/g_whitepap/thermo.htm
↑ http://www.chem.wayne.edu/~hbs/chm6440/PES.gif
↑ K. Fukui, “The path of chemical-reactions - The IRC approach,” Acc. Chem. Res., 14 (1981) 363-68.
↑ Doering WvE, Birladeanu L, Sarma K, Blaschke G,Scheidemantel U, Boese R, Benet-Bucholz J, KlarnerFG, Gehrke J-S, Zimny BU, et al. A non-Cope amongthe Cope rearrangements of 1,3,4,6-tetraphenylhexa-1,5-dienes. J Am Chem Soc 2000, 122:193–203. doi:10.1021/ja993417h

The Diels Alder Cycloaddition

Introduction

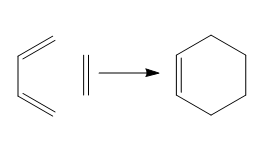
The Diels-Alder reaction is a cycloaddition reaction between conjugated diene and a dienophile. The resulting product is called the adduct. The Diels Alder reaction is the most common example of cycloaddition. Two π systems are involved, one contributing 4 and the other 2 electrons. Since 6 electrons are involved and the reaction is thermally activated it proceeds via a Hückel topology involving only suprafacial components.^[1] The driving force for the reaction is the formation of two new σ-bonds. The two bonds can form from either side of the diene. The one forming from the top is the so called exo-isomer while the one forming from the bottom is the endo-isomer. The exo isomer is generally predicted to be the most stable product, however the endo is the kinetically favourable one due to secondary orbital interactions. For the cycloaddition to work two basic rules about the orbitals symmetry and interactions have to be followed:

the reaction is allowed if the HOMO of one reactant can interact with the LUMO of the other
the HOMO-LUMO can only overlap if there is significant overlap. If the orbitals have different symmetry then no overlap is possible and the reaction is forbidden. In this excercise a prototypical Diels-Alder cycloadditioni is investigated. Then the cycloaddition of molecules carrying substituents are investigated in order to identify secondary orbital overlaps.

Reaction of cyclobutadiene with ethylene

A prototype reaction for the Diels ALder cycloaddition is the one between cyclobutadiene(diene) and ethylene(dienophile). Before looking at the transition state, the two fragments were optimized at the DFT b3lyp/6-31g** level of theory and their HOMO-LUMO pair identified. In the figures below optimized structures and the HOMO-LUMO electron densities can be seen. A Frontier Orbital Representation for the HOMO-LUMO can also be found below. As it can be noted the interaction leading to the cycloaddition is the overlap of the HOMO of the diene and the LUMO of the dienophile. The other interaction will be between the LUMO of the diene and the HOMO of the dienophile.

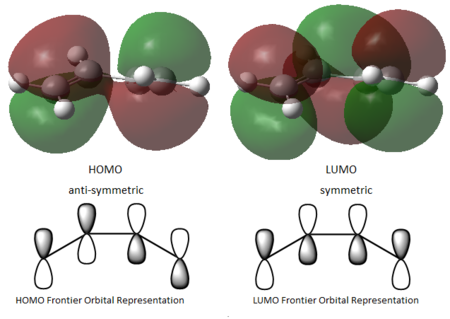The transition state for this Diels-Alder cycloaddition was optimized at the b3lyp/6-31g** level of theory and the structure obtained as well as pictures for the MOs are shown below. As it can be observed the HOMO-1 is the combination of the diene-HOMO and of the dienophile-LUMO, while the LUMO is the combination of the diene-LUMO and the dienophile-HOMO. The calculated HOMO cannot be easily assigned by simply looking at the shape of the orbitals, however a guess for the FMO composition has been drawn.

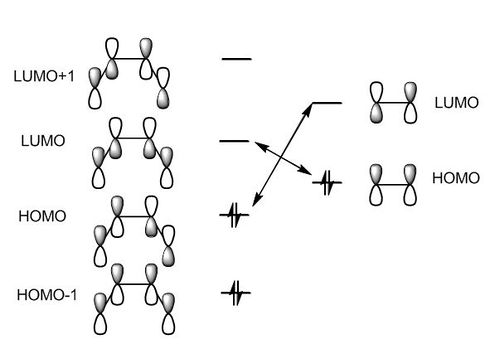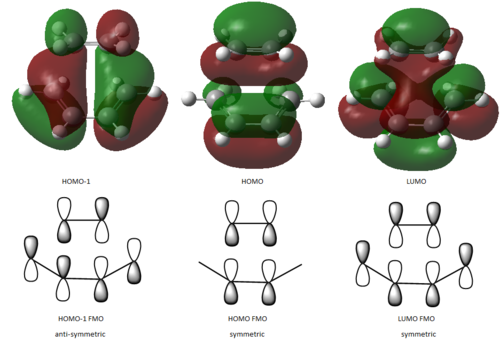Frontier Orbital Diagram, only orbitals with the same symmetry can interact

An animation of the negative vibration for the transitions state can be found here. The negative vibration and its mode confirm convergence of the optimization of the transition state.

The bond lengths for the partially formed sigma bonds are 2.3A. which is less than the sum of the Van der Walls radii for the two Carbon atoms (Carbon VdW radius is 1.7A) indicating partial bond character. The bond length of the C=C double bond in the dienophile is about 1.4A which is slightly longer than the typical 1.3A for a sp². However the bond length of the forming double bond in the diene is also 1.4A which is shorter than the typical 1.5A sp³ bond length. The diene double bonds that are breaking are also 1.4A long which is longer than a typical single bond. Overall all the bonds are about 1.4A. This means that the formation of the transition state is concerted. Observation of the animation suggests that the formation of bonds is synchronous. The lowest energy vibration (twisting) will be fairly excited due to its low frequency vibration, therefore it is supposed to be very fast. However since its mode is normal to the bond-forming vibration it does not affect the formation of the bond.

Reaction of cyclohexa-1,3-diene with maleic anhydride

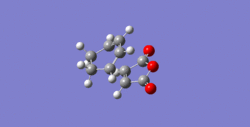
The Diel-Alder cycloaddition for cyclohexa-1,3-diene with maleic anhydride was investigated. The substituents over both the diene and the dienophile are the source of secondary orbtial interactions that give rise to the endo rule.The TS were optimized by QST2 method at the b3lyp/3-21g level of theory. As it was briefly mentioned above two products can be yielded by a Diels Alder cycloaddion depending on the realtive orientations of the π-systems. The transition states for the endo and the exo isomers are shown below.

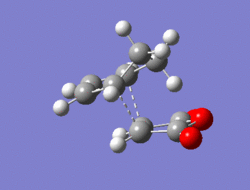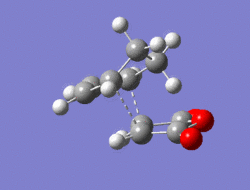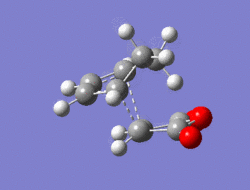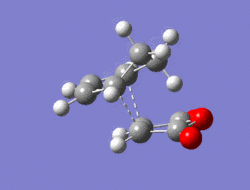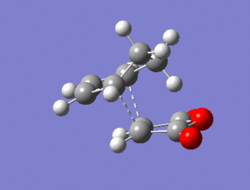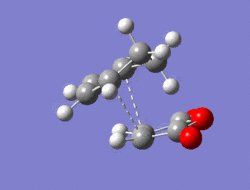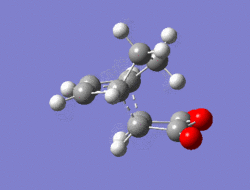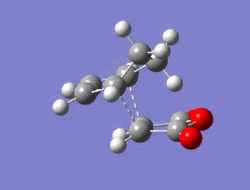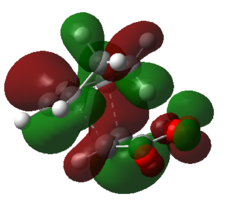For the exo isomer bond formation has two negative vbirational modes, one synchronous at -602cm^-1 and one asynchronous at -21^-1. A better understanding of the asynchronous mode comes from inspection of the HOMO: while one of the forming σ-bonds consists of a fully bonding interaction the other consists of a non bonding interaction, explaining the origin of the asynchronous mode: one bond weakens at the other forms. The energy for the transition state is found to be E=-609.25351 a.u. It can also be noted that the 6-memberred ring is distorted in order to reduce the unfavourable steric interactions between the maleic anhydride and the hydrogens on the adjacent diene carbons. The bond formation for the endo isomer is shown below. It consists of a single synchronous vibrational mode at -362cm^-1. This is in line with the HOMO representation. The calculated energy for the system was E=-609.32100 a.u.

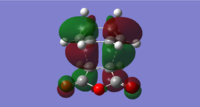The breaking and forming C=C bond lengths are all calculated to be about 1.4 A. as it was noted above this is shorter than a typical C-C single bond but longer than a typical C=C double bond. The distance between the carbons forming σ-bonds is calculated to be 2.1A for the exo and 2.3A for the endo. The larger distance for the endo can be probably be explained by the increased steric repulsion between the two rings that must overlap to form the endo. The energy for the transition state energy is significantly lower for the endo isomer, in fact it is 176kJ/mol lower in energy than for the exo. This calculated value is probably an overestimate but it gives a good idea of the importance of secodary interactions. A frontier orbital representation of the primary and secondary orbital interactions for the endo and the exo isomers is shown below. This representation can be copmpared to the HOMO pictures for the the two isomers: while on the exo the orbital overlap is localized between the carbons forming the new σ bonds, on the endo the orbital overlap is spread over the plane of the 4 carbons of the maleic anhydride.

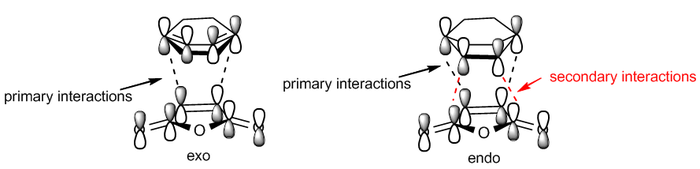
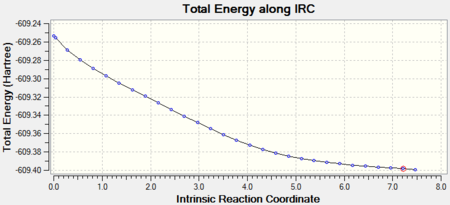
Primary and secondary orbital interactions

In order to visualize the products to which these TS states will lead a IRC calculation in the forward direction was carried out (the backward direction would lead to separation of the fragments). The IRC for the endo and the exo are shown below. The exo-isomer converged to a minimum after 30 steps.

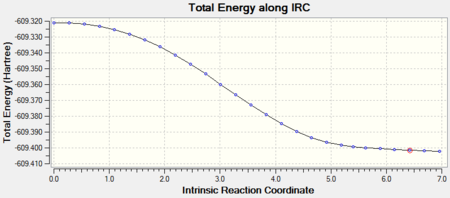
The endo-isomer converged to a minimum after 27 steps.

The structures for the products obtained by IRC are shown here.

The energy obtained is opposite to what was expected, in fact the calculated energy for the exo product is E=-609.39932a.u. while the calculated energy for the endo product is E = -609.40228. The exo product should be more stable than the endo due to reduced unfavourable steric interactions. In fact the substituents on the endo are in axial position which higher in energy than the exo with the substituents in equatorial position. However the IRC might not be complete and hence the structures not fully relaxed.

↑ http://www.ch.ic.ac.uk/local/organic/pericyclic/

SCAN OUTPUT files in D-space

0kelvin_antihexadiene_distorted_b3lyp_631Gd_optfreq http://hdl.handle.net/10042/to-10251
gauche_threefour_15hexadiene_opt http://hdl.handle.net/10042/to-10252
gauche_two_15hexadiene_opt http://hdl.handle.net/10042/to-10253
gauche_three_15hexadiene_opt http://hdl.handle.net/10042/to-10254
gauche_threethree_15hexadiene_opt http://hdl.handle.net/10042/to-10255
anti_two_dist_15hexadiene_opt http://hdl.handle.net/10042/to-10256
anti_two_15hexadiene_opt http://hdl.handle.net/10042/to-10257
anti_three_15hexadiene_opt http://hdl.handle.net/10042/to-10258
gauche_threetwo_15hexadiene_opt http://hdl.handle.net/10042/to-10259
gauche_threeone_15hexadiene_opt http://hdl.handle.net/10042/to-10260

QST2 anti[ci] convergent http://hdl.handle.net/10042/to-10236
boat TS DFT http://hdl.handle.net/10042/to-10235
boat IRC step1 http://hdl.handle.net/10042/to-10234
boat IRC stp2 http://hdl.handle.net/10042/to-10233
chair TS DFT http://hdl.handle.net/10042/to-10239
IRC_reduntantchairTS_200steps_fc_always_threesteps_all http://hdl.handle.net/10042/to-10240
boatTS_IRC_250steps_fc_always http://hdl.handle.net/10042/to-10241
IRC_reduntantchairTS_200steps_fc_always_twosteps http://hdl.handle.net/10042/to-10242
IRC_reduntantchairTS_50steps_fc_once_twosteps http://hdl.handle.net/10042/to-10243
IRC_reduntantchairTS_200steps_fc_once http://hdl.handle.net/10042/to-10244
IRC_reduntantchairTS_50steps_fc_always http://hdl.handle.net/10042/to-10245
IRC_reduntantchairTS_50steps_fc_once http://hdl.handle.net/10042/to-10246
chair_ts_reduntantcoordinate_step2 http://hdl.handle.net/10042/to-10247
chair_ts_reduntantcoordinate http://hdl.handle.net/10042/to-10248
chair_ts_forcematrix http://hdl.handle.net/10042/to-10249
allyl_fragment http://hdl.handle.net/10042/to-10250

[twentyone-1] Cope AC, Hardy EM. The introduction of substituted vinyl groups—a rearrangement involving the migration of an allyl group in a three-carbon system. J Am Chem Soc 1940, 62:441–444. doi: 10.1021/ja01859a055.

[review-2] 2.0 ^2.1 ^2.2 ^2.3 Graulich Nicole. The Cope rearrangement—the first born of a great family. WIREs Comput Mol Sci 2011, 1: 172-190. doi: 10.1002/wcms.17

[ten-3] Pindur U, Schneider GH. Pericyclic key reactions in biological systems and biomimetic syntheses. Chem Soc Rev 1994, 23:409–415. doi: 10.1039/ CS9942300409.

[harrison-4] An introduction to Density Functional Theory, N.M. Harrison 2003, in Computational Materials Science, NATO Science Series III, Ed. Catlow and Kotomin, 187, IOS Press

[becke93-5] Becke,A J. Chem. Phys. 98, 5648 (1993) doi:10.1063/1.464913

[LYP-6] Chengteh Lee, Weitao Yang, and Robert G. Parr, Phys. Rev. B,37,785–789,(1988)

[thermochemistry-7] ttp://www.gaussian.com/g_whitepap/thermo.htm

[PES-8] ttp://www.chem.wayne.edu/~hbs/chm6440/PES.gif

[fukui-9] K. Fukui, “The path of chemical-reactions - The IRC approach,” Acc. Chem. Res., 14 (1981) 363-68.

[doering-10] Doering WvE, Birladeanu L, Sarma K, Blaschke G,Scheidemantel U, Boese R, Benet-Bucholz J, KlarnerFG, Gehrke J-S, Zimny BU, et al. A non-Cope amongthe Cope rearrangements of 1,3,4,6-tetraphenylhexa-1,5-dienes. J Am Chem Soc 2000, 122:193–203. doi:10.1021/ja993417h

[rzepa-11] ttp://www.ch.ic.ac.uk/local/organic/pericyclic/

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[1]

Physical Chemistry Computational Laboratory

The Cope rearrangement

Introduction

Method

Hartree-Fock

Density Functional Theory

Example of Input file

Optimizations

Anti Conformations

Gauche Conformations

DFT investigation of [Ci]anti-1 lowest energy conformer

Optimization

Thermochemistry

Optimizing the "Chair" and "Boat" Transition Structures

"Chair" Transition State optimization

Optimization of the allyl fragment

"Chair" Transition State IRC

"Boat" Transition State optimization

"Boat" Transition State IRC

Transition States Optimization at DFT level of Theory

Tautomerism of the Transition State

The Diels Alder Cycloaddition

Introduction

Reaction of cyclobutadiene with ethylene

Reaction of cyclohexa-1,3-diene with maleic anhydride

SCAN OUTPUT files in D-space

DFT investigation of [C_i]anti-1 lowest energy conformer