Jump to content

Rep:Mod:MRTSFN89

From ChemWiki

Inorganic Chemistry Computational Laboratory

BH3

Optimization

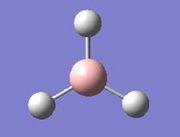
The structure of BH3 was optimized by density functional theory methods. This molecule is the parent compound of the larger class of Boranes. BH3 is only known in the gas phase and it normally dimerises to give diborane. The structure was built in GaussView and then an input file as the one shown below was submitted to Gaussian. 

# opt b3lyp/3-21g geom=connectivity
blank line
 BH3 optimisation
blank line
0 1
 B                  1.45598197    0.12415350    0.00000000
 H                  2.95598197    0.12415350    0.00000000
 H                  0.70598197    1.42319160    0.00000000
 H                  0.70598197   -1.17488461    0.00000000
blank line
 1 2 1.0 3 1.0 4 1.0
 2
 3
 4

The command structure can be briefly described as follows:

  • the key word opt requires optimization of the geometry of the molecule
  • the density functional theory method used for this optimization is b3lyp with basis set 3-21g. B3lyp stands for Becke, 3-parameter,Lee-Yang-Parr. This is a hybrid functional method that includes a mixture of Hartree-Fock and DFT exchange correlations. The general Becke three parameter Hybrid functionals have the following form for the exact energy exchange correlation approxiamation: EXC=a0*EXSlater+(1-a0)EXHF+axΔEXBecke+ECVWN+ac*ΔECnon-local where a0,ax and ac are semiempirical coefficients determined by Becke fitting to the G1 molecule set.[1] HBRLYP is a "flavor" of this hybrid functional, it uses the non-local correlation provided by the LYP [2]expression and VWN functional III for local correlation (instead of V). The correaltion functional used is aCECLYP+(1-aC)ECVWN. Since LYP includes boh local correlation functional, the VWN is used to provide the excess local correlation required since LYP contain a local term equivalent to VWN.
  • geom=connectivity tells the software to read the connectivity of the molecule referring to the last 4 lines of code where the connectivity of each atom is described. In this case for example we have that atom 1 (Boron) is connected to 2 by a single bond (1.0) and so forth.
  • under the first blank line is the title and after the second overall charge and spin are specified. A list of atoms and corresponding coordinates follows.

The geometry of the molecule is subsequently optimized by a DFT self consistent field method. This is a variational approach and on a qualitative level it takes an initial set of orbitals and then modify them until certain convergence criteria are met. Once the calculation has converged an output file is produced where the coordinates for the optimized structure are listed. The last optimization cycle is reported here as an example: 

Berny optimization.
Using GEDIIS/GDIIS optimizer.
Internal  Forces:  Max     0.000413434 RMS     0.000270656
Search for a local minimum.
Step number   4 out of a maximum of   20
All quantities printed in internal units (Hartrees-Bohrs-Radians)
Mixed Optimization -- En-DIIS/RFO-DIIS
Update second derivatives using D2CorX and points    3    4
DE= -1.23D-03 DEPred=-1.73D-03 R= 7.11D-01
SS=  1.41D+00  RLast= 1.03D-01 DXNew= 8.4853D-01 3.0972D-01
Trust test= 7.11D-01 RLast= 1.03D-01 DXMaxT set to 5.05D-01
The second derivative matrix:
                         R1        R2        R3        A1        A2
          R1           0.15486
          R2           0.04153   0.15486
          R3           0.04153   0.04153   0.15486
          A1           0.00000   0.00000   0.00000   0.16000
          A2           0.00000   0.00000   0.00000   0.00000   0.16000
          A3           0.00000   0.00000   0.00000   0.00000   0.00000
          D1           0.00000   0.00000   0.00000   0.00000   0.00000
                         A3        D1
          A3           0.16000
          D1           0.00000   0.00230
ITU=  1  0  1  0
Use linear search instead of GDIIS.
    Eigenvalues ---    0.00230   0.11333   0.11333   0.16000   0.16000
    Eigenvalues ---    0.23793
RFO step:  Lambda= 0.00000000D+00 EMin= 2.30000000D-03
Quartic linear search produced a step of -0.02701.
Iteration  1 RMS(Cart)=  0.00105389 RMS(Int)=  0.00000000
Iteration  2 RMS(Cart)=  0.00000000 RMS(Int)=  0.00000000
ClnCor:  largest displacement from symmetrization is 1.55D-14 for atom     3.
Variable       Old X    -DE/DX   Delta X   Delta X   Delta X     New X
                                (Linear)    (Quad)   (Total)
   R1        2.25537   0.00041   0.00161   0.00000   0.00161   2.25698
   R2        2.25537   0.00041   0.00161   0.00000   0.00161   2.25698
   R3        2.25537   0.00041   0.00161   0.00000   0.00161   2.25698
   A1        2.09440   0.00000   0.00000   0.00000   0.00000   2.09440
   A2        2.09440   0.00000   0.00000   0.00000   0.00000   2.09440
   A3        2.09440   0.00000   0.00000   0.00000   0.00000   2.09440
   D1        3.14159   0.00000   0.00000   0.00000   0.00000   3.14159
        Item               Value     Threshold  Converged?
Maximum Force            0.000413     0.000450     YES
RMS     Force            0.000271     0.000300     YES
Maximum Displacement     0.001610     0.001800     YES
RMS     Displacement     0.001054     0.001200     YES
Predicted change in Energy=-1.071764D-06
Optimization completed.
   -- Stationary point found.

When a stationary point is found it implies that a minimum or a maximum on the potential surface has been met. Whether this is a minimum or a maximum depends on the second derivative which gives the concavity of the well. Positive concavity corresponds to a minimum. Frequency analysis gives some insight in whether a minimum or a maximum have been met, however this will be discussed in more detail later.

A summary of the properties of the optimized borane are reported here: 

BH3 optimisation
File Name = BH3_OPT
File Type = .log
Calculation Type = FOPT
Calculation Method = RB3LYP
Basis Set = 3-21G
Charge = 0
Spin = Singlet
E(RB3LYP) = -26.462 a.u.
RMS Gradient Norm = 0.00020672 a.u.
Imaginary Freq =
Dipole Moment = 0.00 Debye
Point Group = D3H
Job cpu time:  0 days  0 hours  0 minutes 11.0 seconds.

References

  1. ↑ Becke,A J. Chem. Phys. 98, 5648 (1993) doi:10.1063/1.464913
  2. ↑ Chengteh Lee, Weitao Yang, and Robert G. Parr, Phys. Rev. B,37,785–789,(1988)

BH3 Frequency analysis

As briefly mentioned above vibrational analysis is fundamentally the study of the second order derivative of the potential energy surface of the molecule being investigated. When the first derivative fI(x) of a function f(x) is equal to zero then a stationary point has been determined. The identity of the stationary point depends on the concavity of the curve or more precisely on the second derivative fII(x). Depending on whether fII(x) is greater, less or equal to zero the stationary point corresponds to a minimum, a maximum or an inflection point repsectively. The input file for vibrational analysis was of the form: 

# freq b3lyp/3-21g pop=(nbo,full) geom=connectivity

the atomic coordiantes are the same as reported from the output file. The differences with the optimization input file are:

  • the key word freq tells the software to perform vibrational analysis of the molecule
  • pop=(nbo,full) tells the software to perform a full natural bond orbital analysis of the electron density and MOs. The ouptut from this commands will be discussed in a later section.

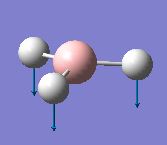
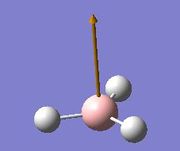
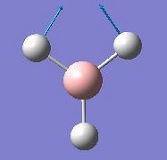
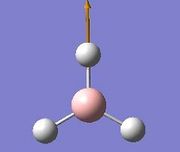
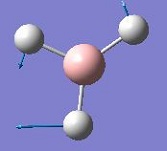
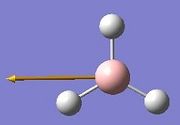
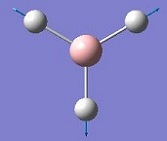
The vibrations identified by vibrational analysis are reported in the scheme below along with their frequency, intensity, symmetry label and dipole derivative unit vector due to the transient variation in dipole.

No form of the vibration Frequency Intensity Symmetry of the vibration Dipole derivative unit vector
1
1144.15 92.8665 A2"
2
1203.64 12.3148 E'
3
1203.64 12.3173 E'
4
2598.42 0.00 A1'
5
2737.44 103.74 E'
6
2737.44 103.7333 E'



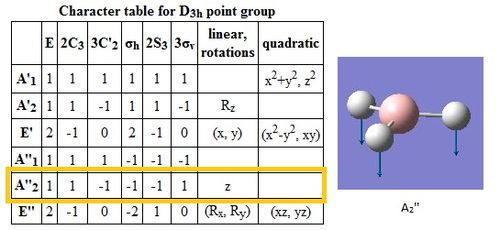
The symmetry label for the vibrations were identified with the help the D3hcharacter table. Each vibration will be represented by one of the irreducible representations of the point group. On the left the character table for D3h and the A2IIvibrations are shown. A2II is a non degenerate representation (contrarily to EI that consists of 3 degenerate vibrations). The symmetry label can be easily assigned by inspection of the table, for A2II for example all the symmetry operations are retained with the exception of the 3C2 rotations around the BH bonds, the σh plane of symmetry and the improper rotations S3. This symmetry properties can be unambiguously assigned to the A2II character.




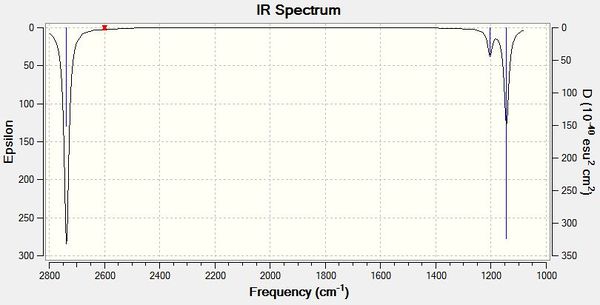
The calculated IR spectrum for BH3 is reported below which shows only three vibrations. This can be explained by noting that vibrations number 4 A1I has no transient dipole moment and that vibrations 2/3 and 5/6 are both degenerate. This could have been inferred by the degenerate representation EI assigned to the vibrations. The reasons why vibration 4 is not active in the IR are discussed further here. Normally for a molecule to be able to interact with an electromagnetic field it must posses a dipole oscillating at the photon frequency ν. This can be understood with a quantum mechanical approach [1]. Let us say that the Hamiltonian of the system has the form 

H=H(0)+H(1)(t)

where H(1)(t) is the time dependent perturbation. Because the perturbation is caused by an oscillating electric field acting on an electric dipole moment we define 

H(1)(t)=-μzEcos(ωt)

where μz is the electric dipole moment of magnitude μz=qR, E is the intensity of the electric field and ω is the oscillating frequency of the incoming field. In classical electromagnetism this expression is equivalent to the potential energy for an electric dipole in an oscillating electric field. We impose as a boundary condition that the perturbation is null at time zero. It can be shown by solution of the time dependent Schroedinger equation that the rate of change of population wf←i of the state ψf due to transition from the state ψi is proportional to the square modulus of the matrix element of the perturbation between the two states: 

wf←i α |Hz,fi(1)|2E2

As in this case the perturbation is that of the interaction of the electromagnetic field with a molecule the rate can be rewritten as 

wf←i α |μz,fi|2E2

Therefore the rate of transition and hence the intensity of the absorption of the incident field (the energy of the incoming field is transformed in work done over the oscillating dipole to redistribute its charge) is proportional to the square of the transition dipole moment 

μz,fi=<ψf|μz|ψi>

The rate of transition is also proportional to the intensity of the oscillating field E2. From this consideration a gross selection rule can be formulated for IR transitions: the electric dipole moment of a molecule must change when the atoms are displaced from one another in order for the vibration to be infra-red active.

Molecular orbitals of BH3

Quantitative and qualitative MOs analysis

Computationally calculating the molecular orbitals shape and energy means solving the Schroedinger equation numerically for a set of electron wavefuntions. While this is not trivial and requires intense computational methods the same can be done on a qualitative level by the construction of a molecualar orbital diagram. Here a molecular orbital diagram for borane has been constructed starting from two simple molecular fragments H3 and a Boron atom. The fundamental concept that makes MO diagrams so qualitatively accurate and powerful is the fact that atomic orbitals of a certain symmetry can only interact with other AOs of the same symmetry, and they can interact only once. Mathematically a MO is a linear combination of atomic orbitals of the form 

ψΓ=N(c1ψ1+c2ψ2+...cnψ2)

where Γ is the symmetry label of the MO, N is a normalization parameter, cn are coefficients that determine how much each atomic orbital contributes to the molecular orbital. The atomic orbitals of a molecule form the basis set for the molecule. To understand the shape of the MOs represented as a combination of AOs in a correlation diagram a few rules have to be made explicit:

  • the AO orbital which is lower in energy makes a larger contribution to the bonding MO
  • the AO which is higher in energy makes a larger contribution to the antibonding MO
  • the larger the orbital overlap the greater the energy splitting
  • the magnitude of orbital overlap depends on several factors such as relative location, orientation and diffusivity of the orbitals involved

Mathematically the splitting is dependent upon the energy difference between the two orbitals ΔE=Ei-Ej, Ei=<ψi|H|ψi>, the exchange integral Hij=<ψi|H|ψj> and the overlap integral Sij=<ψi|ψj>. For degenerate orbitals that interact without overlapping Ebonding=EAO-Hij; for non degenerate non overlapping orbitals Ebonding=E2-(Hij)2/ΔE where ΔE=E2-E1 and E2>E1. Finally for degenerate overlapping orbitals Ebonding=(E+Hij)/(1+Sij) while Eantibonding= (E-Hij)/(1-Sij). From these last relations it can be easily noted that the norm of the energy of the antibonding MO is larger than the norm of the bonding MO. If this effect was reversed dimers of any element with an even number of electrons would be allowed, however since this is not the case elemental dimers with a even number of electrons do not exist in general.

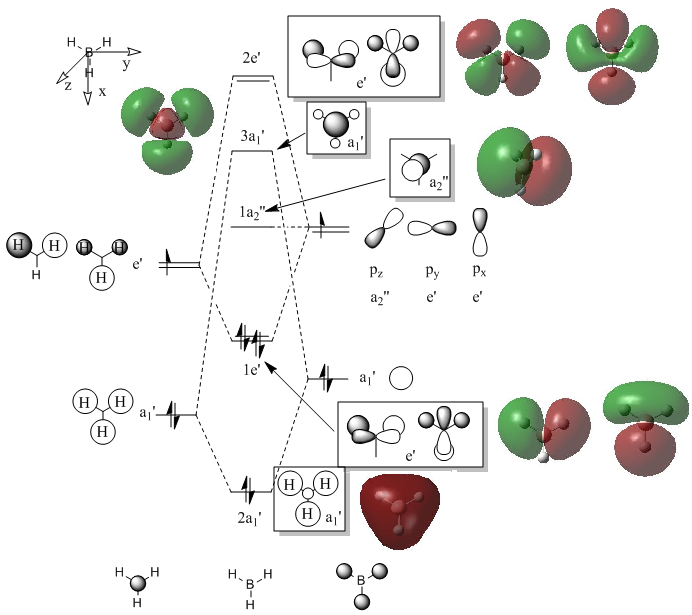
A few comments should be made regarding the molecular orbital diagram above. The energy of the molecular fragment orbital H3 is lower than the boron atomic orbital given the fully bonding interactions between the hydrogens.The antibonding character of the 3a1' and 2e' is difficult to assess by simple inspection. In fact the destabilization energy for each antibonding MO depends on the number of nodes and extent of antibonding interactions i.e. overlap. For both MOs 3 antibonding interactions can be observed (2 for one degenerate form of the 2e' but it is replaced by a node). However one would argue that orbital overlap would be more effective for the e' type orbitals and the number of nodes is also larger. This estimate is in line with the calculated MOs energies. Overall the agreement between calculated energies and predicted order is superb. This supports the idea that MO diagrams are an extremely powerful and useful tool for a chemist. [2]

NBO

The Natural Bonding Orbital analysis gives a molecular illustration which is more similar to a traditional way of thinking about the distribution of electron density in a molecule. The method, in fact, takes the calculated electron density of the MOs and reduces them to the classic natural atomic and hybridized orbitals. NBO provides a great amount of information about the molecule. A review of the NBO analysis output file for BH3 follows:

BH3 has a total of 15 natural atomic orbitals (NAO) listed in the following table. NAOs are listed according to the atom to which they belong to, the orbital angular momentum (s, p, d etc.) the type of orbital (Core, Valence, Rydeberg), the occupancy and finally their energy. Core atomic orbitals are those with lower principal quantum number n than the outermost valence atomic orbitals. Valence orbitals are usually the ones involved in bonding. Ryderberg orbitals are diffused orbitals with principal quantum number n greater than that of any occupied orbital of the ground state. 

NATURAL POPULATIONS:  Natural atomic orbital occupancies
                                                        
  NAO  Atom  No  lang   Type(AO)    Occupancy      Energy
----------------------------------------------------------
    1    B    1  S      Cor( 1S)     1.99903      -6.64475
    2    B    1  S      Val( 2S)     0.96608      -0.09627
    3    B    1  S      Ryd( 3S)     0.00000       0.67666
    4    B    1  px     Val( 2p)     0.85164       0.09607
    5    B    1  px     Ryd( 3p)     0.00000       0.37177
    6    B    1  py     Val( 2p)     0.85164       0.09607
    7    B    1  py     Ryd( 3p)     0.00000       0.37177
    8    B    1  pz     Val( 2p)     0.00000      -0.04532
    9    B    1  pz     Ryd( 3p)     0.00000       0.43446
   10    H    2  S      Val( 1S)     1.11021      -0.05706
   11    H    2  S      Ryd( 2S)     0.00032       0.90015
   12    H    3  S      Val( 1S)     1.11021      -0.05706
   13    H    3  S      Ryd( 2S)     0.00032       0.90015
   14    H    4  S      Val( 1S)     1.11021      -0.05706
   15    H    4  S      Ryd( 2S)     0.00032       0.90015

Inspection of the table above suggests that the Core and Valence orbitals predominate over the Rydeberg type orbitals in describing molecular bonding. This is also summarized in the following table. 

    Natural Population     
--------------------------------------------------------
  Core                       1.99903 ( 99.9517% of   2)
  Valence                    6.00000 (100.0000% of   6)
  Natural Minimal Basis      7.99903 ( 99.9879% of   8)
  Natural Rydberg Basis      0.00097 (  0.0121% of   8)
--------------------------------------------------------

The natural minimum basis set accounts for over 99.98% of the molecular properties. A summary of the natural population is shown below. It reports the natural atomic charges, total core, valence, and Rydberg populations on each atom. The natural charges are equal to the nuclear charge minus the summed natural populations of the NAOs on the atom. Also a visual representation of the natural charges can be produced in GaussView and it is shown below.

visual representation
                                   Natural population summary              
                                                         
                                      Natural Population 
               Natural  -----------------------------------------------
   Atom  No    Charge         Core      Valence    Rydberg      Total
-----------------------------------------------------------------------
     B    1    0.27816      1.99954     2.72230    0.00000     4.72184
     H    2   -0.09272      0.00000     1.09256    0.00015     1.09272
     H    3   -0.09272      0.00000     1.09256    0.00015     1.09272
     H    4   -0.09272      0.00000     1.09256    0.00015     1.09272
=======================================================================
  * Total *    0.00000      1.99954     6.00000    0.00046     8.00000


Finally a summary of the effective valence electron configuration or as defined by the output file "natural electron configuration" is summarized in the following table. It can be noted that the occupancies of atomic orbitals are not integers, however these can be approximated to idealized hybrid or atomic orbitals. For example B has electron configuration: [core]2s( 0.97)2p( 1.70), this can be approximated to the idealized sp2 orbital 

   Atom  No          Natural Electron Configuration
----------------------------------------------------------------------------
     B    1      [core]2S( 0.97)2p( 1.70)
     H    2            1S( 1.11)
     H    3            1S( 1.11)
     H    4            1S( 1.11)

A list of all the NBOs, with their type and occupancy follow. For brevity here we show only the first 4 of the 15 NBOs. Occupancy is shown first, with a label indicating the type of orbitals (BD for 2-center bond, CR for 1-center core pair, LP for 1-center valence lone pair, RY* for 1-center Rydberg, and BD* for 2-center antibond, the unstarred and starred labels corresponding to Lewis and non-Lewis NBOs, respectively)[3] A number indicating the bond order is followed by the atoms to which the NBO is referred to. So for example we have BD ( 1) which means single 2-center bond, B 1 - H 2 between atom B1 and atom H2. The we have an expression for the natural hybrid orbitals NHO written as the linear combination of natural atomic orbitals: 0.6669* B 1 s( 33.33%)p 2.00( 66.67%) + 0.7451* H 2 s(100.00%) where the constants preceding the orbital type are polarization coefficient. In this case for H the polarization coefficient is equal to 0.7451 and it is larger than for B due to the greater electronegativity of Hydrogen. 

      (Occupancy)   Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
    1. (1.99853) BD ( 1) B   1 - H   2 
               ( 44.48%)   0.6669* B   1 s( 33.33%)p 2.00( 66.67%)
                                           0.0000  0.5774  0.0000  0.0000  0.0000
                                           0.8165  0.0000  0.0000  0.0000
               ( 55.52%)   0.7451* H   2 s(100.00%)
                                           1.0000  0.0000
    2. (1.99853) BD ( 1) B   1 - H   3 
               ( 44.48%)   0.6669* B   1 s( 33.33%)p 2.00( 66.67%)
                                           0.0000  0.5774  0.0000  0.7071  0.0000
                                          -0.4082  0.0000  0.0000  0.0000
               ( 55.52%)   0.7451* H   3 s(100.00%)
                                           1.0000  0.0000
    3. (1.99853) BD ( 1) B   1 - H   4 
               ( 44.48%)   0.6669* B   1 s( 33.33%)p 2.00( 66.67%)
                                           0.0000  0.5774  0.0000 -0.7071  0.0000
                                          -0.4082  0.0000  0.0000  0.0000
               ( 55.52%)   0.7451* H   4 s(100.00%)
                                           1.0000  0.0000
    4. (1.99903) CR ( 1) B   1           s(100.00%)
                                           1.0000  0.0000  0.0000  0.0000  0.0000
                                           0.0000  0.0000  0.0000  0.0000

The next segment of the output file summarizes the angular properties of the natural hybrid orbitals. The direction of the bonds are compared with the direction of the internuclear segments and any deviation (bending) are expressed as a deviation angle between the two. For BH3 no deviation from ideality is detected, this information can be used as a probe for successful optimization. 

NHO Directionality and "Bond Bending" (deviations from line of nuclear centers)

        [Thresholds for printing:  angular deviation  >  1.0 degree]
                                   hybrid p-character > 25.0%
                                   orbital occupancy  >  0.10e
                               Line of Centers        Hybrid 1              Hybrid 2
                               ---------------  -------------------   ------------------
               NBO               Theta   Phi    Theta   Phi    Dev    Theta   Phi    Dev
========================================================================================
   None exceeding thresholds

The last interesting segment of the output file is the Perturbation Theory Analysis. This analysis determines all the possible stabilization due to orbital mixing. The stabilization energy is determined by second order perturbation theory. These interactions are referred as "delocalization" corrections to the 0th-order natural Lewis structure.[3] Interaction energies greater than 20Kcal/mol can be considered of interest. 

Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis
    Threshold for printing:   0.50 kcal/mol
                                                                             E(2)  E(j)-E(i) F(i,j)
        Donor NBO (i)                     Acceptor NBO (j)                 kcal/mol   a.u.    a.u.
===================================================================================================
within unit  1
  4. CR (   1) B   1                / 10. RY*(   1) H   2                    1.51    7.54    0.095
  4. CR (   1) B   1                / 11. RY*(   1) H   3                    1.51    7.54    0.095
  4. CR (   1) B   1                / 12. RY*(   1) H   4                    1.51    7.54    0.095

References

  1. ↑ Physical Chemistry, Atkins and De Paula, Oxford University press
  2. ↑ calculation |[DOI:10042/to-http://hdl.handle.net/10042/to-9556]
  3. ↑ 3.0 3.1 http://www.chem.wisc.edu/~nbo5/tutorial.html

Output files

TlBr3 optimization and vibrational analysis

TlBr3 molecule was built in Gaussview. Optimization and frequency analysis were conducted with the following input: 

# opt freq b3lyp/lanl2dz geom=connectivity
blank
TlBr3 optimization and frequency analysis
blank
0 1
Tl                 0.00000000    0.00000000   -0.00000000
Br                 0.00000000    2.69000000   -0.00000000
Br                -2.32960834   -1.34500000   -0.00000000
Br                 2.32960834   -1.34500000   -0.00000000
blank
1 2 1.0 3 1.0 4 1.0
2
3
4
  • The "opt freq" command requests structural optimization and frequency analysis, "b3lyp" is the ab initio DFT method used for the calculation and "lanl2dz" is the basis set of choice. LanL2DZ uses D95V basis set for first row elements[1] and Los Alamos ECP plus MBS on Na-La, Hf-Bi [2] [3] [4]. Since Tallium is between Afnium and Bismut the basis set should be appropriate for the calculation. Los Alamos National Laboratory effective core potential is a basis set that uses pseudo-potentials for a number of elements together with the the appropriate valence basis set. The latter is of double zeta (DZ) quality and combined to the ECB basis set (LANL2) gives the "LANL2DZ" basis set[3]
  • After the first line there is a title
  • 0 1 indicate the charge and the spin respectively
  • The following matrix assigns a coordinate to each atom
  • geom=connectivity tells the software to read the additional lines after the coordinates matrix which defines the bonds for each atom

The overall summary for the calculation is the following: 

File Name = tlbr3_optandfreq
Calculation Type = FREQ
Calculation Method = RB3LYP
Basis Set = LANL2DZ
Charge = 0
Spin = Singlet
Total Energy = -91.218 a.u.
RMS Gradient Norm = 0.00000090 a.u.
Imaginary Freq = 0
Dipole Moment = 0.00 Debye
Point Group = D3h
Job cpu time:  0 days  0 hours  0 minutes 10.0 seconds

It is necessary to use the same method for both optimization and frequency analysis for two reasons:

  • frequency analysis is a probe for successful optimization, hence if a different method were used we would not know whether the optimization has been succesful or not
  • results obtained with different methods are not comparable

As pointed out above vibrational analysis is a probe for successful optimization of the geometry of the molecule. Vibrations are the second derivative of the energy surface over which we optimize our molecule. Second derivative in the description of a mathematical function f(x) describes the curvature or concavity of the function. At f'(x)=0 (first derivative of f(x)) we have a stationary point. A stationary point can either be a minimum, a maximum or a point of inflection depending on whether the second derivative is greater, less or equal to zero respectively. Therefore by analyzing the vibrational modes of our molecule we can asses whether we are at a minimum, at a maximum or if the optimization failed to converge. When all the frequencies are positive we are at a minimum, if one frequency is negative we are at a transition state and if two or more vibrations are negative the optimization has failed to converge.

The vibrations of a molecule have 3N-6 degrees of freedom. The low frequencies are the "-6" frequencies and are the vibration of the molecule around the center of mass. Ideally these frequencies should be equal to zero as the molecule should not move with respect to its center of mass when it vibrates. The low frequencies calculated for TlBr3 are: 

low frequencies = -3.4217   -0.0026   -0.0004    0.0015    3.9359    3.9359

the vibrations are all very close to zero suggesting that the calculation was succesful. The lowest "real" mode is 46.4289 for the E' vibration. The calculated Tl-Br bond length is 2.65A and the bond angle Br-Tl-Br is 120. The bond length determined experimentally was 2.52A[5] therefore the calculated value is within 5% of the experimentally determined value.

What is a bond?

Gaussview does not always draws bonds were expected because the program determines where to display bonds simply by measuring inter-atomic distances. This does not mean that there are no bonds there, in fact bonds are a quantum mechanical concept. Geometry is not always a necessary condition for a bond to exist and neither it is sufficient. Molecular orbitals are diffused over an entire molecule and bonds will be where electron density is localized, if for instance all the MOs of a molecule were summed up we would get a picture that looks something like classical bonds, as the overall electron density is greater where bonds are localized. One of the state of the art approaches that characterize the chemical bonding of a system on the topology of the charge density is the "Quantum Theory of Atoms in Molecules" (AIM). In AIM each atoms acts as a local attractor of electron density and it can be defined in terms of the curvature of electron density. The molecular structure is given by the stationary points of the latter. However to support the idea that geometry is not a sufficient property to decide where the bonds are localized it can be pointed out that very often X-ray crystal structures are misinterpreted, in fact very close atoms could suggest that they are bonded to each other but often it is the case that they are not and they are simply vicinal.


References

  1. ↑ T. H. Dunning Jr. and P. J. Hay, in Modern Theoretical Chemistry, Ed. H. F. Schaefer III, Vol. 3 (Plenum, New York, 1976) 1-28.
  2. ↑ P. J. Hay and W. R. Wadt, “Ab initio effective core potentials for molecular calculations - potentials for the transition-metal atoms Sc to Hg,” J. Chem. Phys., 82 (1985) 270-83. DOI: 10.1063/1.448799
  3. ↑ 3.0 3.1 W. R. Wadt and P. J. Hay, “Ab initio effective core potentials for molecular calculations - potentials for main group elements Na to Bi,” J. Chem. Phys., 82 (1985) 284-98 DOI: 10.1063/1.448800|
  4. ↑ P. J. Hay and W. R. Wadt, “Ab initio effective core potentials for molecular calculations - potentials for K to Au including the outermost core orbitals,” J. Chem. Phys., 82 (1985) 299-310 DOI: 10.1063/1.448975
  5. ↑ Johan Blixt, Julius Glaser, Janos Mink, Ingmar Persson, Per Persson, Magnus Sandstroem,J. Am. Chem. Soc.,1995, 117 (18), pp 5089–5104 DOI:10.1021/ja00123a011

Output files

Isomers of Mo(CO)4L2

Optimization

In this section the relative stability and the vibrational modes of two Mo(CO)4(PPh3)3 isomers are investigated. The cis and trans isomers are expected to have different stability due to the combined back bonding character of the metal carbonyl bond and the trans effect induced by the electron donating PCl3 group. Steric effects are also expected to play a role in the stability of the two isomers, in fact the large size of the PCl3 group will cause deviation from ideality in bond angles and orbital overlap.

The optimization routine was carried on a molecule computationally equivalent, Mo(CO)4(PPh3), This was done to reduce the computational load, in fact by substituting the aryl groups with Chlorine atoms the overall number of electrons is strongly reduced and hence the computation time. Chlorine has been found to have a reasonably similar electronic contribution to PPh3 and in addition it is a very large atom, making the VdW radii of the two groups similar. The optimization consisted of 3 steps:

  • a "loose" optimization at the LanL2MB level of theory (STO-3G on first row, Los Alamos ECP plus MBS on Na-La, Hf-Bi).
  • a ultrafine optimization at the LanL2DZ level of theory with tighter convergence criteria. Convergence was set at 10^-9.
  • a ultrafine optimization at the LAnL2DZ level of theory with tighter convergence criteria and "extrabasis" to include the d-orbitals of the phosphorus atoms

The last optimization step command input was of this type: 

# opt b3lyp/lanl2dz geom=connectivity    int=ultrafine scf=conver=9 extrabasis
(blank line)
title
(blank line)
charge spin
(blank line)
atomic coordinates
(blank line)
connectivity
(blank line)
P 0
D  1  1.0
0.55  0.100D+01
****
(blank line)

the last 5 command lines correspond to the "extrabasis" added to the LanL2DZ basis set. It can be read as: "take the P atoms and add a D function of width 0.55 and decay rate 0.100D+01". The **** tells Gaussian that is the end of the extrabasis command.

A pseudopotential is an effective potential function that replaces the complicated explicit Coloumbic potential of core electrons affected by their relativistic motion. The need for these effective potentials is essential when dealing with heavy atoms. When pseuopotentials are used only the non-core or valence electrons are dealt with explicitly.

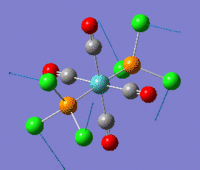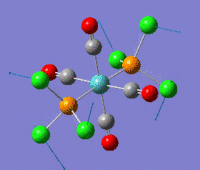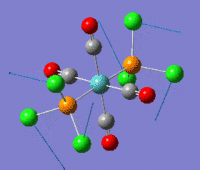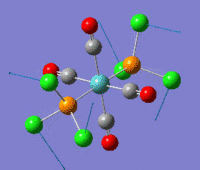
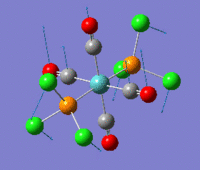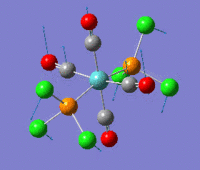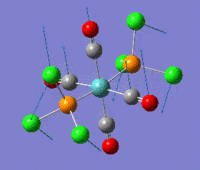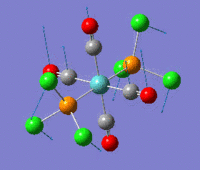
The summaries for the optimization of the cis- and trans- isomers are reported here: 

cis-Mo(CO)4L2 optimization                                      trans-Mo(CO)4L2 optimization
File Name = Mo(CO)4L2_cis_optimization3                         File Name = Mo(CO)4L2_trans_optimization3
File Type = .log                                                File Type = .log
Calculation Type = FOPT                                         Calculation Type = FOPT
Calculation Method = RB3LYP                                     Calculation Method = RB3LYP
Basis Set =lanl2dz+extrabasis                                   Basis Set=lanl2dz+extrabasis                                     
Charge = 0                                                      Charge = 0
Spin = Singlet                                                  Spin = Singlet
E(RB3LYP) = -623.693a.u.                                        E(RB3LYP) = -623.694a.u.
RMS Gradient Norm = 0.00005140 a.u.                             RMS Gradient Norm = 0.00000326 a.u.
Imaginary Freq = 0                                              Imaginary Freq = 0
Dipole Moment = 0.07 Debye                                      Dipole Moment = 0.23 Debye
Point Group = C2                                                Point Group = C2
Job cpu time:  0 days  0 hours 18 minutes 45.9 seconds.         Job cpu time:  0 days  0 hours 24 minutes 34.3 seconds.

Clearly the absolute energy of the two isomers is meaningless as it is in the order of bilion of joules per mole!However the difference between the energy of the two isomers can be insightful. The energies can be converted to kcal/mol as 1a.u.(or Hartree)=2625.49962 kJ/mol. The calculated energy difference is 3.26kJ/mol with the trans-isomer being more stable than the cis. The energy difference is less than the error 10kJ/mol, therefore the two molecules are computationally isoenergetic as their difference in energy is not sufficient to determine unequivocally which isomer is the most stable (at this level of theory). However an interesting exercise can be done assuming that the energy difference of 3.62kJ/mol is real. Assuming that the two isomers can interconvert at room temperature Maxwell-Boltzmann statistics can be used in order to determine the population ratio of cis- to trans- isomer. According to MB statistics the ratio of the population between the excited and the ground state can be defined by the following expression: 

NCis/NTrans=e(-ΔE(j/mol)/(k*Na*T))=e-(3260/(k*Na*298.15))= 0.27

The meaning of this result is that 27% of the overall ground state population(trans-) will be in the cis- form if interconversion between the two isomers is allowed. Although in general energy is an absolute property, in a chemical problem it can be regarded as a difference as it is easier to determine differences than absolute values. To answer the question of whether 3.62kJ/mol is a large amount of energy it can be said that this energy is 1.14kJ/mol greater than thermal energy at 298.25K (Ethermal=kT) or equivalently 3.62kJ/mol correspond to a temperature of 435.38K (162°C). If the two isomers were isoenergetic then the population ratio would be 1. As the calculation above suggests this is not the case and the temperature needs to be raised to 435.38K if to obtain a 1:1 ratio.

cis and trans isomers

As anticipated above a difference in energy between the two isomers was expected due both to the trans effect and to steric repulsion between the bulky groups. Deviation of the bond angles from ideality should reduce orbital overlap. Given the results obtained electronic effect and sterics are equally important. The trans effect will be discussed in the frequency analysis for the two isomers as it has its most obvious manifestation in the carbonyl bond strengths and hence its vibrational frequency. However the presence of steric repulsion can be easily determined by measuring the angle between a PCl3 group and the neighbouring groups. For the cis-isomer the angle between the two M-PCl3 bonds is 94° and the angle of a M-PCl3 bond with the neighboring axial carbonyls is 89° and 92°. For the trans isomer all the bond angles are between 91° and 89°. As expected bond there is greater angular strain for the cis-isomer.

If a catalyst had to be designed and the trans-isomer were to be the most active form of the catalyst (or even the only active one) then the choice of the non carbonyl substituents should be different. A first guess would be to substitute the electron donating PCl3 groups with the electronegative Fluorine. In this way the electronic effect is reversed and the steric strain for the cis-isomer is strongly reduced. The strong electronegativity of fluorine will withdraw electron density from the d-orbitals reducing the back bonding from the metal to the carbonyl and hence it will destabilize the molecule.

cis and trans isomers
Mo(CO)4L2 cis fluoride optimization                          MoCO4L2 trans fluoride optimization 1
File Name = Mo(CO)4L2_cis_fluoride                           File Name = Mo(CO)4L2_trans_fluoride
File Type = .log                                             File Type = .log
Calculation Type = FREQ                                      Calculation Type = FREQ
Calculation Method = RB3LYP                                  Calculation Method = RB3LYP
Basis Set = LANL2DZ                                          Basis Set = LANL2DZ
Charge = 0                                                   Charge = 0
Spin = Singlet                                               Spin = Singlet
E(RB3LYP) = -720.570 a.u.                                    E(RB3LYP) = -720.551 a.u.
RMS Gradient Norm = 0.00001369 a.u.                          RMS Gradient Norm = 0.00001852 a.u.
Imaginary Freq = 0                                           Imaginary Freq = 0
Dipole Moment = 2.65 Debye                                   Dipole Moment = 0.00 Debye
Point Group = C1                                             Point Group = C1
Job cpu time:  0 days  0 hours  8 minutes 42.0 seconds.      Job cpu time:  0 days  0 hours  8 minutes 29.0 seconds.

Mo(CO)4F2 cis and trans isomers were optimized at the same level of theory as for Mo(CO)4(PCl3)2. The results obtained were counterintuitive: the cis isomer is found to be considerably more stable than the trans with a difference in energy of 50kJ/mol. Although steric strain has become less unfavourable for the cis, electronic effects should have predominated making the trans isomer more favourable. However it is found that two Fluorine atoms trans to each other constitute a very unfavorable configuration. This can be proved by inspection of the metal to fluorine bond length. The M-F bond lengths are 1.97A and 1.99A for the cis and the trans isomers respectively. The M-F symmetric and asymmetric vibrations are respectively 582cm-1-symmetric and 609cm-1-asymmetric for the cis and 552cm-1-symmetric and 554cm-1-asymmetric for the trans. Therefore the covalent character and hence the strength of the bond is lower in the trans isomer. It has been shown that using very electronegative substituents will reverse the order of stability.

Frequency Analysis

Frequency analysis was performed for the two isomers. The same level of theory as for the last step of the optimization routine was used: DFT-b3lyp with LanL2DZ basis set, tighter convergence criteria (=10^-9) and "extrabasis" to include the d-orbitals of the phosphorus. The symmetry of the vibrations have been assigned referring to the highest symmetry possible for the two isomers, C2v for the cis-isomer and D4h for the trans. This was done with the help of the character tables for C2v and D4h symmetry in the same fashion as it had been done for BH3. The vibration frequencies and intensities, as well as the symmetry labels and their representation are shown in the following table.

cis-No form of the vibration Frequency (cm-1) Intensity Symmetry of the vibration trans-No form of the vibration Frequency (cm-1) Intensity Symmetry of the vibration
1-cis
1938 1605 B1 1-trans
1939 1606 Eu
2-cis
1942 812 B2 2-trans
1939 1606 Eu
3-cis
1952 588 A1 3-trans
1966 6 B1g
4-cis
2019 544 A1 4-trans
2025 5 A1g

The energy frequencies of the equatorial carbonyl stretches are higher in energy for the cis than for the trans, with the exception of the vibration number 4 which is higher in energy in the trans-isomer. The bond length of the equatorial carbonyl bonds is found to be 1.18A for the cis (cf.lit. cis 1.14)[1]and 1.17A for the trans, the slightly longer bond in the trans isomer explains the slightly lower vibrational energies. The metal to carbon bonds are found to be 2.02A and 2.06A (cf.lit. cis 2.03A)[1] long for the cis and trans isomers respectively. This can be explained by trans-effect, in fact since the phosphorus is coordinated to the metal by donation of a lone pair, this donates electron density in the d-orbital to which it is coordinated. Broadly speaking two trans groups share the same d-orbital. Bearing in mind that the carbonyl is a good π-acceptor, the excessive electron density will contribute to the backbonding to the carbonyl group. This will result in two effects: shortening of the M-C length and lengthening of the C=O bond as electron density is being donated in the C=O π* orbital. Both effects are observed. Comparison to the literature are made for the cis-isomer referring to Mo(CO)4(PPh3)2.

The carbonyl region of the IR spectra are shown in the figure below. As it can be seen the cis-isomer shows 4 characteristic peaks corresponding from left to right to the vibrations 4,3,2 and 1-cis. On the other hand due to the higher symmetry of the trans-isomer only only three peaks should be visible although one peak is visible corresponding to the degenerate modes 1 and 2-trans. Vibration 3 and 4-trans are not sufficiently IR active to be observed. The frequencies measured in the second year lab were ν(cm-1)=2010, 1896, 1887, 1839 (cf. lit.ν(cm-1)=2023, 1929, 1911, 1899)[2] for the cis isomer and ν(cm-1) =2013, 1945, 1889 (cf. lit.ii ν(cm-1) =1945, 1889)[2] for the trans isomer. The calculated frequencies are in good agreement with the experimental values and the literature, considered that the frequencies reported in the literature and measured experimentally refer to Mo(CO)4(PPh3)2. In the literature only 2 peaks were measured for the trans isomer. The literature seems to be in disagreement with both the experimental results and the calculated modes as 3 different peaks are predicted. The calculation suggests that vibrations 3-trans and 4-trans are very weak in intensity and hence weakly IR active, however these modes are experimentally visible probably due to distortion of the molecule. Symmetry arguments could also be used, in fact a peak should be visible for each IR-active mode.


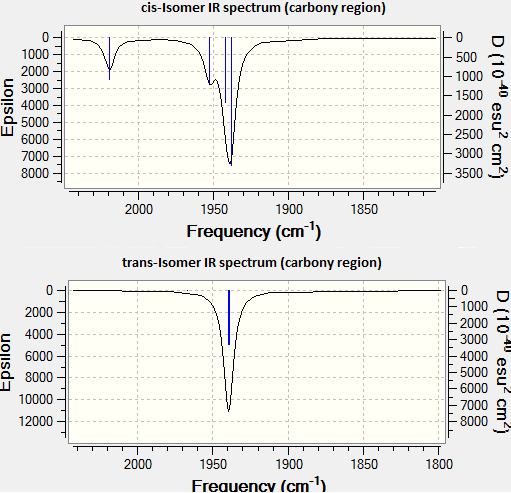
All the calculated vibrations are positive. This means that the calculations have converged to a minimum. A number of low frequency vibrations were observed and they are summarized in the table below. The lowest two correspond to the rotation of the PCl3 groups while the third one corresponds to distortion of the plane of the molecule to minimize steric strain. The temperature necessary to excite a molecule as if it was in the field of a photon of frequency 10cm-1 can be easily found: T=hν/kb=14K. This gives an idea of what temperatures are required to excite this sort of vibrations. These vibrations will be excited at room temperature and the PCl3 groups will rotate freely. Furthermore given the distortion from the plane of the molecule the two isomers will probably quickly interconvert at 298K. This result is in line with the relative energies of the two isomers found above.

cis-No form of the vibration Frequency (cm-1) Intensity trans-No form of the vibration Frequency (cm-1) Intensity
1-cis
12 0.016 1-trans
5 0.055
2-cis
20 0.004 2-trans
7 0.000
3-cis
46 0.001 3-trans
40 0.113

References

  1. ↑ 1.0 1.1 F. Albert. Cotton, Donald J. Darensbourg, Simonetta. Klein, Brian W. S. Kolthammer Inorg. Chem., 1982, 21 (1), pp 294–299 DOI:10.1021/ic00131a055
  2. ↑ 2.0 2.1 F. A. Cotton, , Inorg . Chem. 1964, 3, 702 DOI:10.1021/ic50015a024

Output files

Seven Coordinate neutral interhalogens: geometry, electronics and relative stabilities

Introduction

Diatomic interhalogens XY have been observed for all combination of the elements, but many of them show very short lifetimes. Interhalogens with the central atom in a intermediate oxidation state have been observed for several halogens, these are ClF3, BrF3, ClF5, BrF5and IF5. Some of them form dimers such as I2Cl6 or long polymeric chains like IF3. Most of the higher oxidation state interhalogens are fluorides and the only neutral species with the central atom in oxidation state +7 is iodine. Both Chlorine and Bromine are known in the oxidation state +7 only in the negatively charged perchlorate ions. In this work the reasons why IF7 is an isolable compund while BrF7 and ClF7 are not is investigated by a theoretical/computational approach with the help of density functional theory methods. As it will be seen, the work aimed to the optimization of the heptavalent interhalogen compounds but this was only successful for IF7. Interestingly a reaction was "filmed" instead for BrF7 and ClF7.

Method

Structures for the three interhalogen compounds were built using GaussView. A multi-step optimization routine was used to optimize the molecules. The method adopted was DFT-B3YLP. The optimization followed a logical stepwise process of the following form (the choice of basis sets was customized for each type of atom):

  • 1 optimize with basis sets: 6-31G for F and LanL2MB for halogen
  • 2 frequency analysis with basis sets: 6-31G for F and LanL2MB for halogen.

-TS check: If a transition state is found, displace the atoms in the direction indicated by the displacement vectors of the imaginary vibration using the GaussVIew tool in the vibrations interface and re-optimize at the same level of theory as for the last step. If the molecule returns to the starting point open the output file, copy the displacement vector for the imaginary vibrations, multiply by two and add to the atomic coordinates of the molecule. Then reoptimize at the same level of theory as for the last step.

  • 3 optimize with basis sets: 6-311G(d,p) for F and LanL2DZ for halogen
  • 4 frequency analysis with basis sets: 6-311G(d,p) for F and LanL2DZ for halogen

-TS check

  • 5 optimize with basis sets: 6-311G(d,p) for F and appropriate Stuttgart/Dresden pseudopotential for halogen(MW46 for iodine, MW28 for bromine and MW10 for Chlorine).
  • 6 frequency analysis with basis sets: 6-311G(d,p) for F and appropriate Stuttgart/Dresden pseudopotential for halogen(MW46 for iodine, MW28 for bromine and MW10 for Chlorine).

-TS check

  • 7 optimize with basis sets: 6-311G(d,p) for F and appropriate Stuttgart/Dresden pseudopotential for halogen(MW46 for iodine, MW28 for bromine and MW10 for Chlorine). Use ultrafine convergence criteria.
  • 8 frequency analysis with basis sets: 6-311G(d,p) for F and appropriate Stuttgart/Dresden pseudopotential for halogen(MW46 for iodine, MW28 for bromine and MW10 for Chlorine). Use ultrafine convergence criteria.

-TS check

A number of delicacies have been used when writing the input files. This is best explained by showing an example. For completeness the input file for step 7 of iodine will be shown: 

#p opt ub3lyp/gen nosymm geom=connectivity pseudo=read int=ultrafine scf=conver=11
(blank line)
IF7 fourth optimization
(blank line)
0 1
F                  0.00000100    1.97599600    0.00000200
F                  1.87928600    0.61066700   -0.00000200
F                 -0.00000100   -0.00006000    1.92456400
F                  1.16148700   -1.59860300    0.00000100
F                 -1.16148700   -1.59860300    0.00000100
F                 -0.00000100   -0.00006000   -1.92456300
F                 -1.87928600    0.61066600   -0.00000200
I                  0.00000000   -0.00000400    0.00000000
(blank line)
1 8 1.0
2 8 1.0
3 8 1.0
4 8 1.0
5 8 1.0
6 8 1.0
7 8 1.0
8
(blank line)
F 0
6-311G(d,p)
****
I 0
MWB46
****
(blank line)
I 0
MWB46

The features of the input file above are the following:

  • the #p instead of a simple # calls for an extended printout, specifically it switches on the printing of the SCF convergence
  • the u in front of b3lyp stands for unrestricted and it tells Gaussian to take into accouny electron correlation and hence to calcualte the MOs for every single electron, rather than for a pair. This gives different orbitals for different spins, one for the α and one for the β electron. Since these molecules are not paramagnetic this is not particularly important.
  • the /gen means that the basis set is customized and found at the bottom of the input file
  • nosymm tells Gaussian to carry out the optimization regardless of any possible symmetry
  • geom=connectivity refers tot he atoms connectivity shown under the atoms coordinates
  • pseudo=read tells Gaussian to read at the end of the input file for the ECP
  • int=ultrafine scf=conver=11 as above means stricter convergence criteria than by default
  • at the end of the input file F 0 6-311G(d,p) tells gaussian to use 6-311G(d,p) basis set for fluorine atom while I 0 MWB46 tells Gaussian to use the explicit component (not the pseudo potential) of MWB46 basis set for iodine. These commands refer to the "gen" keyword
  • the last two lines refer to the pseudo=read command and tells Gaussian to take MWB46 as the pseudopotential. Gauussian will only take the implicit part of the basis set (which is the pseudopotential).

IF7

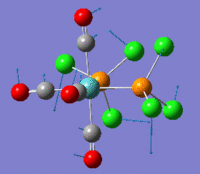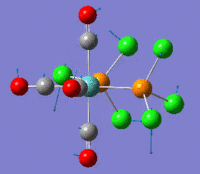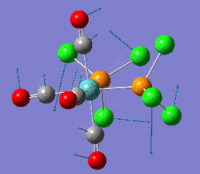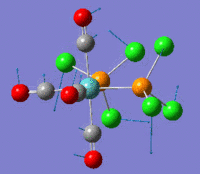
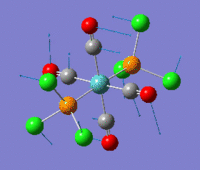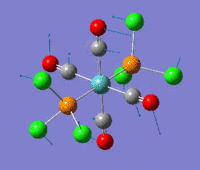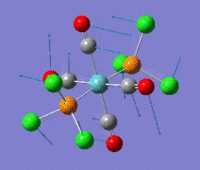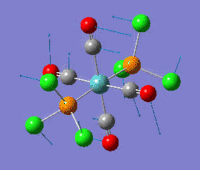
The optimization routine described above was successfully carried out for IF7. In the figure below a representation of the various optimization steps can be observed. Although negative frequencies were measured already at low level of theory, distortion of the geometry of the molecule was only preformed after the highest level of theory, calculation-step7 (the reason is that I had not realized!). This should have not affected the outcome of the optimization.

As it can be observed in the representation above the molecule distorts from pentagonal bipyramidal (PB) to distorted capped octahedral (CO). This is in disagreement with VSEPR theory that predicts PB geometry. Two negative vibrations were observed for structure 3: -67cm-1 and -66 cm-1. As it can be noted by observation of the vibrations, the molecule tends to distort the co-planar fluorine atoms.

Structure3 -67cm-1
Structure3 -66cm-1

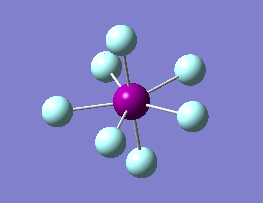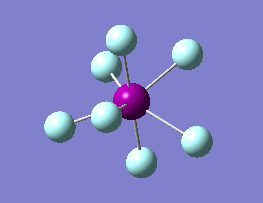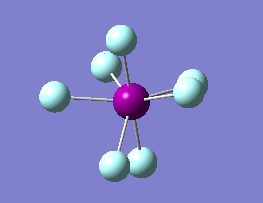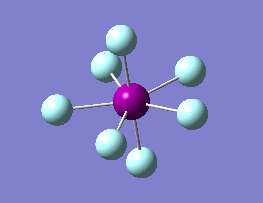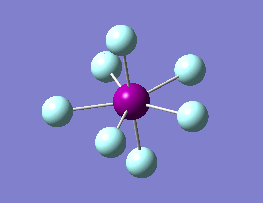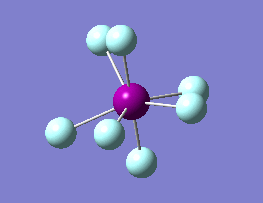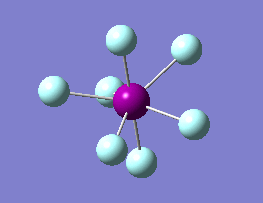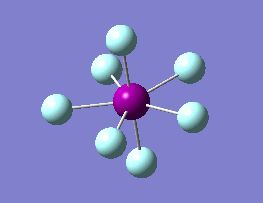A natural bond orbital analysis was conducted on the molecule in order to understand the nature of the hypervalency of the molecule. A summary of the Natural Population Analysis is reported below:

Natural Charge
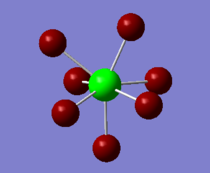
                        Natural Population
               Natural  -----------------------------------------------
   Atom  No    Charge         Core      Valence    Rydberg      Total
-----------------------------------------------------------------------
     F    1   -0.47639      1.99998     7.47030    0.00611     9.47639
     F    2   -0.46426      1.99998     7.45828    0.00599     9.46426
     F    3   -0.47611      1.99998     7.47002    0.00611     9.47611
     F    4   -0.46151      1.99999     7.45590    0.00563     9.46151
     F    5   -0.46418      1.99998     7.45821    0.00598     9.46418
     F    6   -0.46424      1.99998     7.45826    0.00599     9.46424
     F    7   -0.47604      1.99998     7.46994    0.00611     9.47604
     I    8    3.28273     46.00000     3.69492    0.02235    49.71727
=======================================================================
  * Total *    0.00000     59.99989    55.93584    0.06427   116.00000

As it could have been expected, given the strong electronegativity of the fluorine atoms and the great polarizability of the iodine atom the bonds have a very large ionic character. Also the Natural electron configuration can give some insight: 

   Atom  No          Natural Electron Configuration
----------------------------------------------------------------------------
     F    1      [core]2S( 1.96)2p( 5.51)
     F    2      [core]2S( 1.97)2p( 5.49)
     F    3      [core]2S( 1.96)2p( 5.51)
     F    4      [core]2S( 1.97)2p( 5.49)
     F    5      [core]2S( 1.97)2p( 5.49)
     F    6      [core]2S( 1.97)2p( 5.49)
     F    7      [core]2S( 1.96)2p( 5.51)
     I    8      [core]5S( 1.48)5p( 2.22)6p( 0.02)

From the Natural electron configuration it can be seen that only 4 electrons are effectively left in the iodine 5s(1.48)5p( 2.22) orbitals, supporting the idea of mostly ionic bond. The normal valency of iodine is 1. The calculated natural charge of Iodine is +3 which means that we might as well be looking at IF43+...3F-. However this is still hypervalent, in fact the calculated valence of Iodine is 3.69, hence 4. Iodine's hypervalency has been confirmed.

BrF7

The optimization process for BrF7 is shown in the Figure below. As it can be observed the optimization routine "films" a reaction. The heptavalent Bromine is very unfavourable, first it deforms from from PB geometry to CO geometry. Then as structure 4 has an imaginary vibration the atomic coordinates are modified once by the 1xdisplacement-vector to return 5 and since it has gone back to the transition state the coordinates are modified by 2xdisplacement-vector to yield the dissociated product 6. The molecule dissociates producing a pentavalent Bromine with square pyramidal structure and a F2 molecule . However this geometry is in not in accordance with VSEPR theory. In the absence of more accurate calculations it can be checked whether this geometry is more favourable than trigonal bipyramidal. Evaluation of the energy for the two geometries suggests that square pyramidal is lower in energy: -512.315a.u. for trigonal bypiramidal and -512.337a.u. for square pyramidal. This corresponds to a difference in energy of 58kJ/mol which is a very large difference.

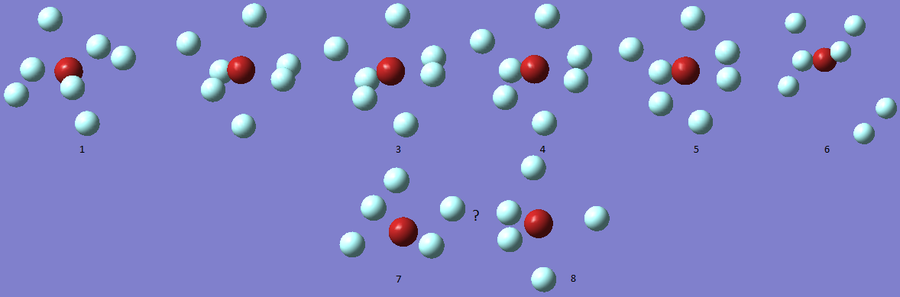
The imaginary vibrations for structures 1 and 5 are shown below. In order to obtain the dissociated structure the displacement vector for the third vibration had to be multiplied by two.

Structure1 -54cm-1
Structure1 -38cm-1
Structure5 -8cm-1

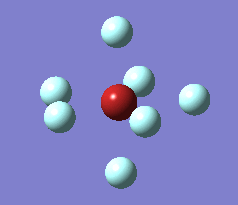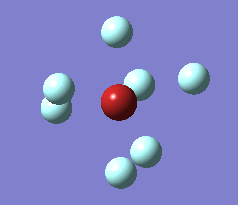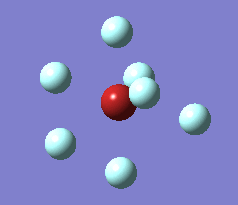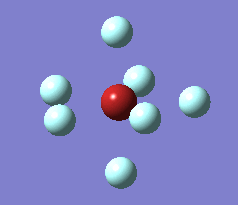Although BrF7 is found to be too unfavorable to be optimized, BrF5 is still hypervalent as the normal valency of halogens is 1. A natural population summary is reported below. The natural charge on the central halogen is only +2 as two fluorines have been removed. This is in accordance with what was found for iodine: if each fluorine atom has a a charge of about -0.5 then dissociation of 2 fluorine atoms will reduce the natural charge to +2. 

               Natural  -----------------------------------------------
   Atom  No    Charge         Core      Valence    Rydberg      Total
-----------------------------------------------------------------------
     F    1   -0.43990      1.99999     7.43571    0.00421     9.43990
     F    2   -0.43999      1.99999     7.43580    0.00421     9.43999
     F    3   -0.43990      1.99999     7.43571    0.00421     9.43990
     F    4   -0.44000      1.99999     7.43580    0.00421     9.44000
     F    5   -0.34305      1.99999     7.33719    0.00587     9.34305
    Br    6    2.10284     28.00000     4.87290    0.02426    32.89716
=======================================================================
  * Total *    0.00000     37.99994    41.95310    0.04696    80.00000

The formal charge of the fluorines is still about -0.5, however it is found to be slightly smaller than for Iodine, probably due to the lower polarizability of Bromine. Given the natural charges one might be tempted to rewrite BrF5 as BrF32+...2F-. This is indeed correct, in fact halogens have 7 electrons and the valence electrons for Bromine are calculated to be 4.87≈5. Of the five remaining electrons bromine will retain two and it will form 3 covalent bonds with the other 3. Overall bromine is found to be less hypervalent than Iodine. Hypervalency of Iodine was found to be 4 while the hypervalency of Bromine is 3. The natural electron configuration for BrF5 is also reported below. 

   Atom  No          Natural Electron Configuration
----------------------------------------------------------------------------
     F    1      [core]2S( 1.98)2p( 5.46)
     F    2      [core]2S( 1.98)2p( 5.46)
     F    3      [core]2S( 1.98)2p( 5.46)
     F    4      [core]2S( 1.98)2p( 5.46)
     F    5      [core]2S( 1.98)2p( 5.36)
    Br    6      [core]4S( 1.89)4p( 2.98)5p( 0.02)

ClF7

Heptavalency becomes increasingly unfavourable as we go up in the group. In fact while Bromine requires the highest level of theory to detect the unstability of the capped octahedral structure, chlorine shows the need of dissociation already when the LanL2DZ basis set is used. The optimization route is shown graphically in the figure below. Here as above the final product 7 is square pyramidal,not in accordance with VSEPR theory. While frequency analysis shows that the two geometries are both minima, the square pyramidal one is found to be lower in energy: -513.801a.u. for trigonal bypiramidal and -513.818a.u. for square pyramidal. This is equivalent to a difference in energy of 45kJ/mol.

Optimization at the Lan2DZ level of theory finds two degenerate imaginary vibrations. Observation of the distortions suggests that the fluorine atoms do not simple need to distort from the plane but they need to dissociate.

Structure2 -523cm-1
Structure2 -523cm-1

Th hypervalency of ClF5 is finally investigated. A summary of the Natural Population calculated by NBO is shwon below. Chlorine shows a hypervalency similar to that of Bromine, in fact the Chlorine's natural charge can be approximated to +2 and the formula rewritten as ClF32+...2F-. However since the charge of Chlorine is not fully +2 (due to its lower polarizability) the nature of one of the ionic interactions will be between that of an ionic and a covalent bond. This is confirmed by the fact that slightly more than 5 valence electrons are calculated for chlorine (5.39). This means that the hypevalency of Chlorine will be slightly higher than 3. 

               Natural  -----------------------------------------------
   Atom  No    Charge         Core      Valence    Rydberg      Total
-----------------------------------------------------------------------
     F    1   -0.34113      1.99999     7.33694    0.00419     9.34113
     F    2   -0.34114      1.99999     7.33696    0.00419     9.34114
     F    3   -0.23129      1.99999     7.22672    0.00457     9.23129
     F    4   -0.34116      1.99999     7.33698    0.00419     9.34116
     F    5   -0.34115      1.99999     7.33696    0.00419     9.34115
    Cl    6    1.59587     10.00000     5.39083    0.01330    15.40413
=======================================================================
  * Total *    0.00000     19.99997    41.96539    0.03464    62.00000

A summary of the Natural electron condfiguration is shown below: 

   Atom  No          Natural Electron Configuration
----------------------------------------------------------------------------
     F    1      [core]2S( 1.99)2p( 5.35)
     F    2      [core]2S( 1.99)2p( 5.35)
     F    3      [core]2S( 1.99)2p( 5.24)
     F    4      [core]2S( 1.99)2p( 5.35)
     F    5      [core]2S( 1.99)2p( 5.35)
    Cl    6      [core]3S( 1.91)3p( 3.48)4p( 0.01)

Overall the order of hypervalency is the following: I(4) > Cl(3<v<4) > Br(3).

Relative stabilities

The initial purpose of the project was to compare the relative stability of the three heptavalent interhalogens. However it was found that only Iodine can be heptavalent. However the optimization summaries for the three hypervalent compound are here reported and the energies can be compared. 

IF7                                       BrF5                                        ClF5
Calculation Method = UB3LYP               Calculation Method = RB3LYP                 Calculation Method = RB3LYP
Basis Set = Gen                           Basis Set = Gen                             Basis Set = Gen
Charge = 0                                Charge = 0                                  Charge = 0
Spin = Singlet                            Spin = Singlet                              Spin = Singlet
E(UB3LYP) = -710.047 a.u.                 E(RB3LYP) = -512.337 a.u.                   E(RB3LYP) = -513.818a.u.
RMS Gradient Norm =  a.u.                 RMS Gradient Norm = 0.00006850 a.u.         RMS Gradient Norm = 0.00006269 a.u.
Imaginary Freq = 0                        Imaginary Freq = 0                          Imaginary Freq = 0
Dipole Moment = 0.35 Debye                Dipole Moment = 2.31 Debye                  Dipole Moment = 1.26 Debye
Point Group = C1                          Point Group = C1                            Point Group = C1
Job cpu time: 3 minutes 38.4 seconds.     Job cpu time: 3 minutes 22.4 seconds.       Job cpu time:  1 minutes  3.3 seconds.

Energy is reported in Hartree with 3 significant figures, in fact an error of 10kJ/mol corresponds to an error of about 0.005a.u. While IF7 cannot be compared to the other two compounds, as they contain a different number of atoms, ClF5 is found to be lower in energy than BrF5. The reason for extra stability is probably the fact that bonds in ClF5 are more covalent in character and as noted above the compound is more hypervalent than BrF5.

Berry Pseudorotation

The Berry pseudorotation is a vibration causing molecules of certain geometries to isomerize by exchanging two axial ligands with two equatorial ligands. Two low energy vibrations have been identified for the square pyramidal structures of both BrF5 and ClF5. The vibrations are excited at 173cm-1 for both molecules. These vibrations if frozen when at the far left in the representation would give a trigonal bipyramidal geometry (clearly this is true as long as the central atom adjusts).Two of the equatorial fluorines become axial while the remaining two equatorial atoms and the axial fluorine atom become for the trigonal plane.For these reasons these vibrations are thought to be the ones that lead to Berry-pseudorotation.

BrF5 Berry-Pseudorotation -173cm-1
ClF5 Berry-Pseudorotation -173cm-1

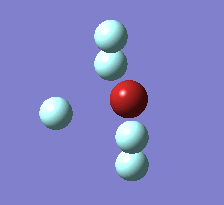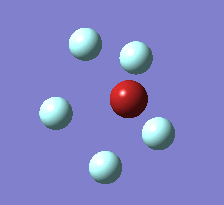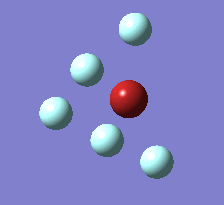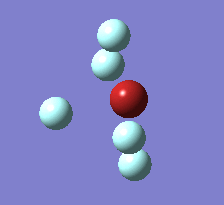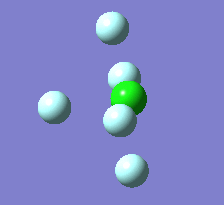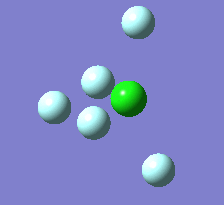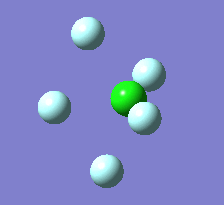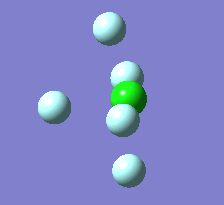This shows that the two structures can indeed isomerise even though the square pyramidal is the most stable configuration.

Output files

The output files are listed in the order they have been produced. opt and freq indicate optimization and frequency respectively. dist means that the molecule has been distorted because a transition state has been met. doubledisplaces means that the molecule has been distorted by displacing the atoom by twice the displacement vector of the imaginary vibration of the transition state. pop refers to the pop=(full,nbo) command. If the freq file is not listed it means that it is part of the optimization file. IF7 output files

BrF7 output files

BrF5 output files

ClF7 output files

ClF5 output files

Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:MRTSFN89&oldid=817462"