Rep:Mod:MM2jht

Ammonia (NH₃)

A frequency and optimization analysis was carried out on ammonia using Gaussian Calculation. The results obtained are presented below:

Key Information

Calculation method: RB3LYP

Basis set: 6-31G(d,p)

Final Energy E(RB3LYP): -56.55776873 a.u.

RMS gradient: 0.00000485 a.u.

Point group of your molecule: C_3V

N-H Bond Length = 1.01798 Å (within reasonable range (±5%) of literature values of 1.008 Å and 1.012Å)

N-H Bond Angle = 105.745° (within reasonable range (±5%) of literature values of 107.3° and 106.67°)

Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES

The optimisation file is available here

Rotatable Model of Ammonia

Vibrational Information

Literature values obtained from http://cccbdb.nist.gov/exp2.asp?casno=7664417, within ±5% of obtained values. Mode 1(Lit.) corresponds to Mode 4, Mode 2(Lit.) corresponds to Mode 1, Mode 3(Lit.) corresponds to modes 5 and 6, Mode 4(Lit.) corresponds to Modes 2 and 3

Modes of vibration expected from 3N-6 rule = 6 (N=4 for 4 atoms in ammonia)

Degenerate modes: Modes 2-3 are degenerate, Modes 5-6 are degenerate

Bending vibrations: Modes 1-3

Stretching vibrations: Modes 4-6

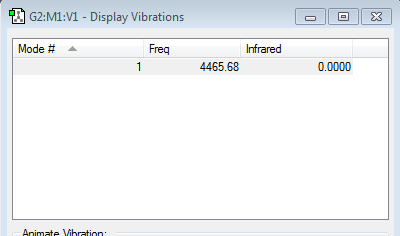
Mode that is highly symmetric: Mode 4

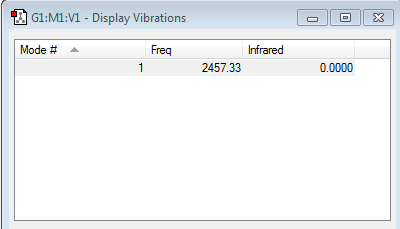
'Umbrella' mode: Mode 1

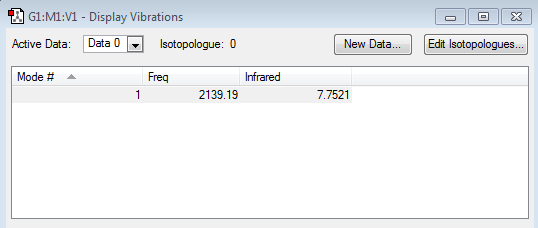
Bands expected in experimental spectrum of gaseous ammonia = 2 (as shown in the spectra below)

The modes at 3461.29 cm ^-1 and 3589.82 cm ^-1 are not observed since their intensities are too low. This is due to the fact that these stretching modes only involve a small change in dipole moment and thus, do not show intense peaks in the spectrum.

The 2 modes at 1693.95 cm ^-1 appear as a single peak since they are degenerate. Thus, only 2 peaks at 1089.54 cm ^-1 and 1693.95 cm ^-1 are visible, giving 2 bands.

Charge Distribution

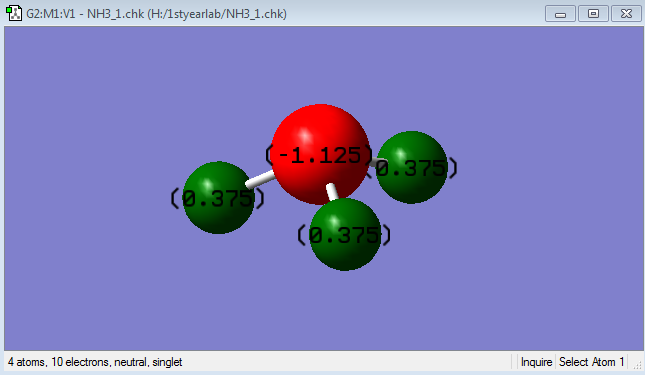
N is expected to be negatively charged whereas H is expected to be positively charged since N is more electronegative than H. Thus, it will draw electron density towards itself.

Charge of N = -1.125

Charge of H = +0.375

Nitrogen (N₂)

A frequency and optimization analysis was carried out on nitrogen using Gaussian Calculation. The results obtained are presented below:

Key Information

Calculation method: RB3LYP

Basis set: 6-31G(d,p)

Final Energy E(RB3LYP): -109.52412868 a.u.

RMS gradient: 0.00000003 a.u.

Point group of your molecule: D_∞h

N-N Bond Length = 1.10550 Å (within reasonable range (±5%) of literature values of 1.0975 Å and 1.098 Å)

Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES

The optimisation file is available here

Rotatable Model of Nitrogen

Vibrational Information

• Lit. value = 2359 cm^-1

Which is expected since there is only 1 vibrational mode for N₂ (stretching mode).

However, the vibration will not appear in an IR spectrum since it does not involve a change in dipole moment.

Hydrogen (H₂)

A frequency and optimization analysis was carried out on hydrogen using Gaussian Calculation. The results obtained are presented below:

Key Information

Calculation method: RB3LYP

Basis set: 6-31G(d,p)

Final Energy E(RB3LYP): -1.17853936 a.u.

RMS gradient: 0.00000017 a.u.

Point group of your molecule: D_∞h

H-H Bond Length = 0.74279 Å (within reasonable range (±5%) of literature values of 0.741 Å)

 Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES

The optimisation file is available here

Rotatable Model of Hydrogen

Vibrational Information

• Lit. value = 4401 cm^-1

Which is expected since there is only 1 vibrational mode for H₂ (stretching mode).

However, the vibration will not appear in an IR spectrum since it does not involve a change in dipole moment.

Haber-Bosch Process

Reaction Equation:

N₂ + 3H₂ → 2NH₃

Energy calculations

E(NH₃) = -56.55776873 a.u.

2*E(NH₃) = -113.11553746 a.u.

E(N₂) = -109.52412868 a.u.

E(H₂) = -1.17853936 a.u.

3*E(H₂) = -3.53561808 a.u.

ΔE = 2*E(NH₃) - [E(N₂) + 3*E(H₂)] = -113.11553746 - [(-109.52412868) + (-3.53561808)] = -0.0557907 a.u.

= -146.48 kJ mol^-1

Thus, the ammonia product is more stable than the gaseous reactants since energy is released in the reaction.

Cyanide Ion (CN^-)

A frequency and optimization analysis was carried out on the cyanide anion using Gaussian Calculation. The results obtained are presented below:

Key Information

Calculation method: RB3LYP

Basis set: 6-31G(d,p)

Final Energy E(RB3LYP): -92.82453153 a.u.

RMS gradient: 0.00000704 a.u.

Point group of your molecule: C_∞V

C-N Bond Length = 1.18408 Å (within reasonable range (±5%) of literature values of 1.14 Å and 1.177 Å)

Item               Value     Threshold  Converged?
 Maximum Force            0.000012     0.000450     YES
 RMS     Force            0.000012     0.000300     YES
 Maximum Displacement     0.000005     0.001800     YES
 RMS     Displacement     0.000008     0.001200     YES

The optimisation file is available here

Rotatable Model of CN Anion

Note: Grey Atom represents C, Blue Atom represents N (also for all subsequent diagrams)

Vibrational Information

• Lit. value 2035 cm^-1

Which is expected since there is only 1 vibrational mode for CN (stretching mode).

The vibration will appear in the IR spectrum since it involves a change in dipole moment. (As shown in the spectrum below)

Charge Distribution

A charge of -0.754 is observed for the N atom, while a charge of -0.246 is observed for the C atom.

This is expected since the charges add up to -1. Also, since N is more electronegative, it will pull the electron density of the molecule towards itself and thus have a higher charge.

Molecular Orbitals

Molecular Orbital Diagram for Valence Electrons of CN^-

Diagram taken from: http://chemistry.stackexchange.com/questions/18449/cyanide-ion-non-bonding-lone-pair

There is mixing between 3σ and 5σ molecular orbitals, causing the 5σ orbital to be higher in energy than the 1π orbitals.

Molecular Orbital Surfaces

Note: Bond is along the x-axis for the following diagrams

3σ of CN^-

3σ of CN^-

The 3σ of CN^- is formed from the linear combination of 2s orbitals from C and N respectively.

It is a bonding orbital since the overlap of the two 2s orbitals result in the electron density of the molecular orbital being localized in between the two atoms.

There is larger electron density on the nitrogen atom since it is more electronegative, which causes it to withdraw electron density towards itself.

4σ^* of CN^-

4σ^* of CN^-

The 4σ^* of CN^- is formed from the linear combination of 2s orbitals from C and N respectively.

It is an anti-bonding orbital since the overlap of the two 2s orbitals result in the electron density being localized on the individual atoms, with a nodal place in between the atoms. Thus, it has a higher energy than the 3σ orbital.

There is larger electron density on the carbon atom since it is less electronegative.

Due to the presence of 2 electrons in this M.O., the overlap between the 2s atomic orbitals does not result in a bond between C and N.

1π of CN^-

1π of CN^-

There are two 1π orbitals for CN^-. They are each formed from the linear combination of 2p_y orbitals from C and N, and from the combination the 2p_z orbitals. Thus, they are degenerate, both having the same energy of -0.01696 a.u. However, both orbitals lie in different planes. (only 1 representation is shown above since both have the same shapes)

The 1π orbitals are bonding orbitals since the overlap of the two 2p_y and two 2p_z orbitals result in the electron density of the molecular orbital being localized in between the two atoms.

5σ of CN^- (HOMO)

5σ of CN^-

The 5σ of CN^- is formed from the linear combination of 2p_x orbitals from C and N.

It is a bonding orbital since the overlap of the two 2p_x orbitals result in the electron density being localized in between the 2 atoms (i.e. a bond) and is the Highest Occupied Molecular Orbital (HOMO) of CN^-.

There is larger electron density on the carbon atom, which is less electronegative, even though it is a bonding orbital. However, this is reasonable since C acts as the nucleophilic site in CN^- as it forms a bond with other molecules.

2π^* of CN^- (LUMO)

2π^* of CN^-

There are two 2π^* orbitals for CN^-. They are each formed from the linear combination of 2p_y orbitals from C and N, and from the combination the 2p_z orbitals. Thus, they are degenerate, both having the same energy of 0.35435 a.u. However, both orbitals lie in different planes. (only 1 representation is shown above since both have the same shapes)

Both are anti-bonding orbitals since there is a nodal plane between the C and N atoms. The size of the orbital is larger on the Carbon atom since it is less electronegative.

The 2π^* is the Lowest Unoccupied Molecular Orbital of CN^-, as seen from the image above.

Bond Order

In the valence molecular orbital, there are 8 electrons in the bonding orbitals (3σ, 5σ and 1π), and 2 electrons in the anti-bonding orbitals (4σ^*)

Bond order = (8-2)/2 = 3

Thus, a triple bond, contributed by the Linear Combination of Atomic Orbitals of the 2p orbitals, is observed for CN^-.

Methyl Lithium (CH₃Li)

A frequency and optimization analysis was carried out on Methyl Lithium using Gaussian Calculation. The results obtained are presented below:

Key Information

Calculation method: RB3LYP

Basis set: 6-31G(d,p)

Final Energy E(RB3LYP): -47.40616301 a.u.

RMS gradient: 0.00005818 a.u.

Point group of your molecule: C_3V

C-Li Bond Length = 1.97800 Å

C-H Bond Length = 1.10031 Å

Li-C-H Bond Angle = 112.483°

H-C-H Bond Angle = 106.299°

• Bond angle between Li-C-H is larger since Li is a larger atom than H. Hence, there is more repulsion between the substituents, causing it to have a larger angle.

 Item               Value     Threshold  Converged?
 Maximum Force            0.000112     0.000450     YES
 RMS     Force            0.000052     0.000300     YES
 Maximum Displacement     0.000296     0.001800     YES
 RMS     Displacement     0.000162     0.001200     YES

The optimisation file is available here

Rotatable Model of MeLi

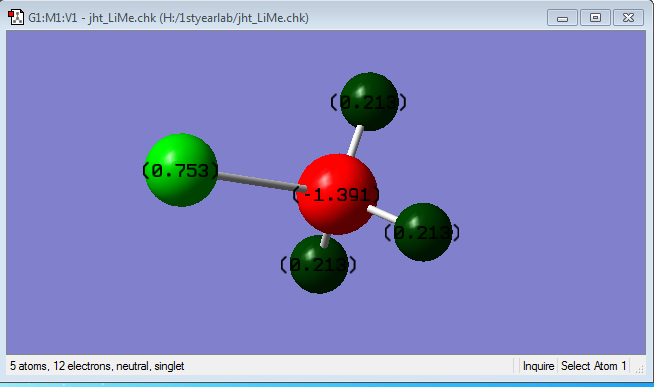
Note: Grey Atom represents C, White Atom represents H, Purple Atom represents Li

Vibrational Information

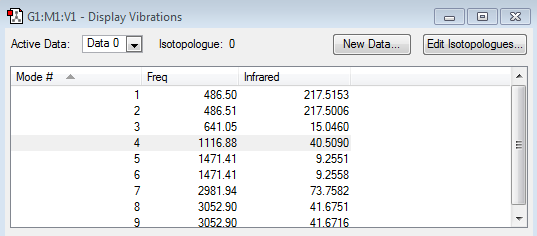
According to the 3N-6 rule, number of vibrational modes = 3(5)-6 = 9

This is in agreement with the number of vibrational frequencies shown above.

6 bands are observed from the spectrum. This is because Modes 1-2 are degenerate; Modes 5-6 are degenerate; and Modes 8-9 are degenerate because they occur at the same frequencies respectively.

Charge Distribution

A charge of -1.391 is observed for the C atom, while a charge of 0.213 is observed for the H atom, and a charge of 0.753 for the Li atom.

This is expected since the charges add up to 0. Also, since C is more electronegative than both Li and H, it will pull the electron density of the molecule towards itself and thus have a negative charge.

Molecular Orbitals

Molecular Orbital Surfaces

Note: Bond is along the x-axis for the following diagrams

Highest Occupied Molecular Orbital of MeLi

From the diagram above, much of the electron density of the H.O.M.O. is located between the C-Li bond. Thus, this is the nucleophilic site when Methyl Lithium acts as a nucleophile, and the C-Li bond breaks.

This is as expected since C is more electronegative than Li.

Lowest Unoccupied Molecular Orbital of MeLi

The L.U.M.O. has the largest orbital surface on the Li atom. Hence, when the C-Li bond breaks, Li will act as an electron acceptor, forming an Li⁺ ion; whereas C will act as an electron donor to the species reacting with MeLi.