Rep:Mod:MLN2
Energy and frequency calculations
BH3
Calculation and basis set: B3LYP/6-31G(d,p)
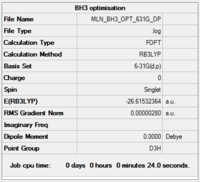
Item Value Threshold Converged? Maximum Force 0.000012 0.000450 YES RMS Force 0.000008 0.000300 YES Maximum Displacement 0.000064 0.001800 YES RMS Displacement 0.000039 0.001200 YES
Low frequencies --- -2.2126 -1.0751 -0.0055 2.2359 10.2633 10.3194 Low frequencies --- 1162.9860 1213.1757 1213.1784
Optimised BH molecule |
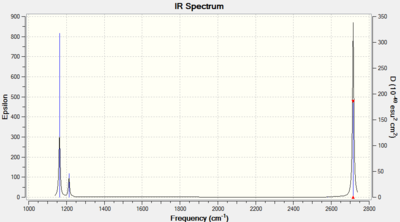
Vibrations and IR spectrum for BH3
| Mode number | Wavenumber (cm-1 | Intensity (arbitrary units) | Symmetry | IR active? | Type |
| 1 | 1163 | 93 | A2 | Yes | Out-of-plane bend |
| 2 | 1213 | 14 | E' | Very slight | In-plane bend |
| 3 | 1213 | 14 | E' | Very slight | In-plane bend |
| 4 | 2582 | 0 | A1' | No | Symmetric stretch |
| 5 | 2715 | 126 | E' | Yes | Asymmetric stretch |
| 6 | 2715 | 126 | E' | Yes | Asymmetric stretch |
|
BH3 has six normal vibrational modes, following the 3N-6 rule, which can be seen above. However, only five are IR active, two of which are only very slightly active. Mode 4 is not IR active, and so does not show up in the spectrum, because it is a symmetric B-H stretching mode so there is no overall change of dipole moment. Following the same idea, the modes that are only slightly active (2 and 3) have a very small overall change in dipole moment and thus a small intensity. Modes 2 & 3 and 5 & 6 are degenerate, each pair have the same wavenumber, so only one peak, per pair, will show in the spectrum which corresponds to both modes. Thus, the three peaks seen in the spectrum correspond to (with increasing wavenumber) mode 1, modes 2&3, and modes 5&6.
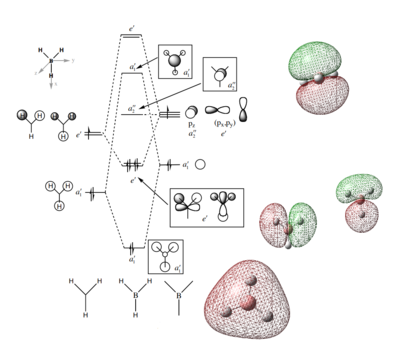
Molecular orbital diagram
MO diagram of BH3
Ng611 (talk) 21:21, 20 May 2018 (BST) Good analysis, although you needed to include the MOs for the highest energy antibonding orbitals.
The computed MOs can be seen next to a qualitative MO diagram of BH3, which has suggested MOs drawn on. The computed MOs are very similar, suggesting that MO theory is extremely useful and powerful, in that it can predict the shape of MOs which allows us to predict where electron density is around atoms in a molecules, and thus allows us to predict reactivities and properties of molecules and compounds. The only slight difference is the size of the orbitals, however this is likely due to the convention of drawing orbitals centered around their central atom to make the drawing clearer. The computed MOs are more diffuse, such as the MOs that are based on the Boron also encompassing a lot of the hydrogen atom, as opposed to just covering the Boron. The computed MOs also show the difference in size contribution from Boron and Hydrogen, as the number of electrons that are formally from Hydrogen is smaller so will contribute less, as opposed to the Hydrogen and Boron having the same size atomic orbitals and neither dominating the molecular orbitals.
Ng611 (talk) 21:22, 20 May 2018 (BST) Excellent explanation!
NH3
Calculation and basis set: B3LYP/6-31G(d,p)
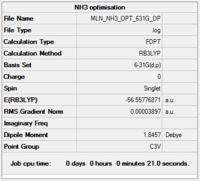
Item Value Threshold Converged? Maximum Force 0.000046 0.000450 YES RMS Force 0.000032 0.000300 YES Maximum Displacement 0.000437 0.001800 YES RMS Displacement 0.000215 0.001200 YES
Low frequencies --- -30.2800 -30.2661 -0.0032 0.0083 0.0488 6.6346 Low frequencies --- 1088.6566 1694.0289 1694.0292
Optimised NH molecule |
NH3BH3
Calculation and basis set: B3LYP/6-31G(d,p)
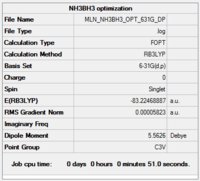
Item Value Threshold Converged? Maximum Force 0.000137 0.000450 YES RMS Force 0.000038 0.000300 YES Maximum Displacement 0.001015 0.001800 YES RMS Displacement 0.000224 0.001200 YES
NH3BH3 frequency analysis file
Low frequencies --- -0.1843 -0.0663 -0.0075 10.2238 16.5669 16.5817 Low frequencies --- 263.0245 631.3830 638.8701
Optimised NHBH molecule |
Association energy
Calculating the assosiation energy of NH3BH3:
The equation for assosiation energy is: ΔE=E(NH3BH3)-[E(NH3)+E(BH3)]
-| Energy | Energy value /a.u. | E(NH3BH3) | -83.22469 |
|---|---|---|---|
| E(NH3) | -56.55777 | ||
| E(BH3) | -26.61532 | ||
| ΔE=E(NH3BH3)-[E(NH3)+E(BH3)] | -0.05160 |
| ΔE | -135 kJ/mol |
Here, the association energy of NH3 and BH3 is ca;culated, which corresponds to the bond strength of the dative N-B bond formed between the fragment molecules. The dative bond is weaker than a standard single bond, such as a CH bond at around 413 kJ/mol[2], however it is stronger than an intermolecular force bond such as a hydrogen bonds, which can range from -4 to -50 kJmol.[3]
Ng611 (talk) 21:24, 20 May 2018 (BST) Good calculation and very good comparison to the literature. Well done for using a text source too!
Pseudo potential basis set calculations
BBr3
Calculation and basis set: B3LYP/6-31G(d,p)LANL2DZ
A pseudo potential basis set, LANL2DZ, was used on the Bromine atoms, to take their heavier size and greater number of electrons into account, as the standard basis set, 6-31G(d,p), is not sufficient for Bromine, but is still appropriate for Boron.
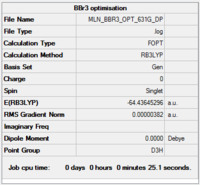
Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000036 0.001800 YES RMS Displacement 0.000023 0.001200 YES
BBr3 Optimization file: DOI:10042/202384
BBr3 Frequency analysis file: DOI:10042/202385
Low frequencies --- -0.0137 -0.0064 -0.0046 2.4315 2.4315 4.8421 Low frequencies --- 155.9631 155.9651 267.7052
Optimised BBr molecule |
Ionic Liquids
Optimization and frequency analysis
[N(CH3)4]+
Calculation and basis set: B3LYP/6-31G(d,p)
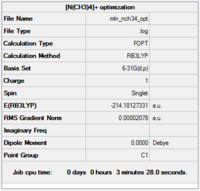
Item Value Threshold Converged? Maximum Force 0.000075 0.000450 YES RMS Force 0.000017 0.000300 YES Maximum Displacement 0.001604 0.001800 YES RMS Displacement 0.000478 0.001200 YES
[N(CH3)4]+ frequency analysis file
Low frequencies --- -13.0688 -0.0004 0.0007 0.0011 9.0649 17.6599 Low frequencies --- 184.1917 284.8215 288.7061
Optimised [N(CH)] molecule |
[P(CH3)4]+
Calculation and basis set: B3LYP/6-31G(d,p)
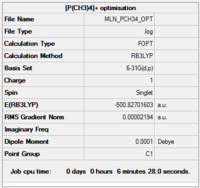
Item Value Threshold Converged? Maximum Force 0.000140 0.000450 YES RMS Force 0.000033 0.000300 YES Maximum Displacement 0.000758 0.001800 YES RMS Displacement 0.000298 0.001200 YES
[P(CH3)4]+ frequency analysis file
Low frequencies --- -25.0682 -0.0018 0.0028 0.0029 11.5007 23.6958 Low frequencies --- 156.2201 192.2968 193.0216
Optimised [P(CH)] molecule |
Charge analysis
NBO Charges
Charge distribution in [N(CH3)4]+: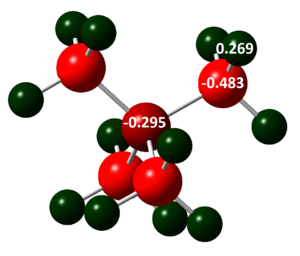 
and [P(CH3)4]+: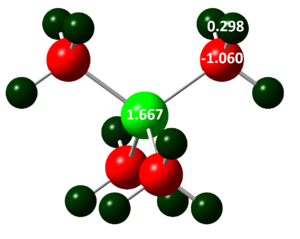 
The colours of the atoms correspond to charges and are the same for [N(CH3)4]+ and [P(CH3)4]+. Colour/charge range is from red/ -0.483, to black/ 0.000, to green/ 1.667. The colour range was kept the same to allow the charge distribution to be compared. The Phosphorous atom is much more positively charged (+1.667) than the Nitrogen atom (-0.295) in their respective cations, this is likely due to the greater electronegativity of Nitrogen compared to Phosphorous, so the Nitrogen will pull more electrons towards itself. Phosphorous is also a lot larger and softer, and therefore more polarisable so it is easier for the neighboring atoms to pull electron density away from it, creating a positive dipole. The Carbon in the Nitrogen containing cation is less negatively charged (-0.483) than in the Phosphorous containing cation (-1.060). This again shows the polarisiability and lesser electronegativity of Phosphorous as compared to Nitrogen. Because Phosphorous is more polarisiable, the carbon bonded to Phosphorous can pull more electron density onto itself. The hydrogen atoms in both cations have similar charges (0.269 and 0.298). Due to the separation of the Hydrogens and the central atoms, they are only affected by their neighboring atom which is Carbon in both, so a big difference is not expected.
Ng611 (talk) 21:31, 20 May 2018 (BST) What about the summation of partial charges? It might seem trivial, but it should be highlighted.
This charge distribution analysis can be used in designing ionic liquids, as the positive charged must be delocalised over the entire molecule in order to have a high melting point. Thus, the Phosphorous cation would not be suitable because the charge is localized and so the anions in the mixture would form formal ionic bonds to the Phosphorous cation. The nitrogen cation would however be suitable, but better cations can be designed too. By substituting the methyls for more electron withdrawing groups that are also delocalised, such as pyridine, the positive charge is further distributed and ionic liquids can be designed with melting points up to hundreds of degrees. [4]
On the nitrogen containing cation, the formal charge is usually placed on Nitrogen, however it can clearly be seen that this is not valid as the nitrogen actually has a negative dipole in the compound. It is usually depicted this way due to the Nitrogen donating its lone pairs to form the fourth bond, and thus a 'positive charge' is produced ,as an electron is somewhat removed from the Nitrogen in order to share it with another atom. However, this description can still be useful as the Nitrogen atom is still more positive than the Carbon atoms to which it is bonded, so of the central atoms it does have the relative positive dipole. The most positive atoms in this cation are actually the hydrogens, due to their low electronegativity.
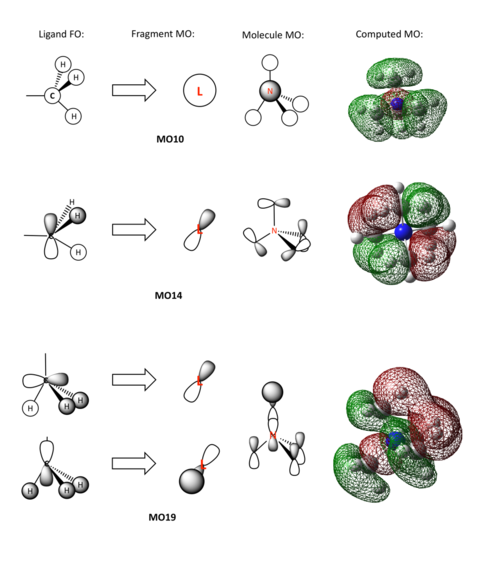
[N(CH3)4]+ Molecular Orbitals
The molecular orbitals of [N(CH3)4]+, show the distribution of electrons around the cation, and a selection can be seen below. The electron distribution seen here, supports the statements made about charges above.
In this diagram, the linear combination of atomic orbitals has been used to create fragment orbitals and then molecular orbitals, which have then been compared to the computed molecular orbitals. Above, the LCAO and computed MOs can be seen for MOs 10, 14, and 19. MO 19 was chosen as it portrays the most bonding character. This is the only MO with no nodes across bonds, which would weaken, what would formally be called a bond, between atoms. These three MOs also show a variety of p and s orbitals being combined to produce complex MOs, wchi distribute electrons all around the molecules, as opposed to just between each pair of atoms. It can also be seen that there is no lack of electron density at the Nitrogen, suggesting that there is not a 'positive charge' located at the nitrogen. The formal positive charged just means that there is one less electron in the whole system than would be expected from summing all the electrons in each atom.
Ng611 (talk) 21:30, 20 May 2018 (BST) Excellent MO/FO analysis, really well done!
Ng611 (talk) 21:35, 20 May 2018 (BST) Overall, this was a near perfect report, with only an incomplete BH3 MO analysis and a missing bit for your ionic liquids charge analysis preventing you from getting full marks. You should be very proud of this work.
References
- ↑ http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year2a/Tut_MO_diagram_BH3.pdf
- ↑ Yu-Ran Luo and Jin-Pei Cheng "Bond Dissociation Energies" in CRC Handbook of Chemistry and Physics, 96th Edition
- ↑ missing author1 (2002). "The Hydrogen Bond in the Solid State". [[Angew. Chem. Int. Ed. (journal)|Angew. Chem. Int. Ed.]] 41: 48–76. doi: <48::AID-ANIE48>3.0.CO;2-U 10.1002/1521-3773(20020104)41:1<48::AID-ANIE48>3.0.CO;2-U.
- ↑ https://pubs.acs.org/doi/abs/10.1021/ja0619612