Rep:Mod:MLN
Optimising Haber-Bosch Molecules
NH3
-
Before optimisation with bond lengths 1.30 Å
-
Optimisation intermediate step geometry 1
-
Optimisation intermediate step geometry 3: bonds are visualised as the atoms are within Gaussian's bonding distance.
-
Optimisation intermediate step geometry 5: H-N-Lone pair bond angle decreases
-
Optimisation intermediate step geometry 7: Fully optimised structure

Properties
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final energy E(RB3LYP) | -56.55776873 a.u. |
| RMS Gradient | 0.00000485 |
| Point Group | C3V |
| Optimised N-H bond length | 1.01798 Å |
| Optimised H-N-H bond angle | 105.741° |
A literature value for the average N-H bond length is 1.012 Å[1] which shows the Gaussian calculation is quite accurate. A literature value for the H-N-H bond angle is 106.7°[2] which show thats the Gaussian calculation is a good approximation for the angle but not perfect.
"Item" table from log file:
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
NH molecule |
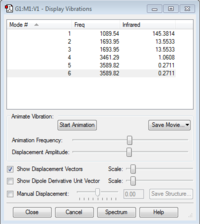
Vibrational Modes
Using the 3N-6 rule we expect 6 vibrational modes as there are 4 atoms. Modes 2 and 3 are degenerate, and 5 and 6 are degenerate, as they have the same frequency and IR number so, therefore, will have the same energy as frequency and energy are proportional. Modes 1, 2, and 3 are "bending" vibrations whereas modes 4, 5, and 6 are "bond stretch" vibrations. Mode 4 is also highly symmetric. Mode 1 is known as the "umbrella" mode. 4 bands would be expected to be seen in an experimental spectrum of gaseous ammonia as there are 4 distinct vibrational frequencies at which ammonia absorbs EM radiation, as 2 sets of the 6 modes are degenerate.
Charge Analysis
The image shows the charge distribution found on NH3 for the different atoms. It would be expected for the Nitrogen atom to have a negative charge as it is the more electronegative atom and so will pull more of the electron density towards itself, and therefore the Hydrogen atoms would be expected to have positive charges.
N2

Properties
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final energy E(RB3LYP) | -109.52412868 a.u. |
| RMS Gradient | 0.00000060 |
| Point Group | D*H |
| Optimised N-N bond length | 1.10550 Å |
| Optimised N-N bond angle | 180° |
A literature value for the N-N bond length is 1.10 Å[3] showing that the Gaussian calculation is again a good approximation.
"Item" table from log file:
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
N molecule |
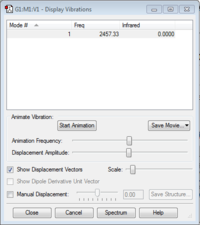
Vibrational Modes
Nitrogen only has one vibrational mode as it is a linear molecule and the IR value is zero as there is no absorption because there is no change in dipole moment.
H2

Properties
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final energy E(RB3LYP) | -1.17853936 a.u. |
| RMS Gradient | 0.00000017 |
| Point Group | D*H |
| Optimised H-H bond length | 0.74279 Å |
| Optimised H-H bond angle | 180° |
A literature value for the H-H bond is 0.74 Å[4], again showing that the Gaussian calculation is a good aroximation for the bond length.
"Item" table from log file:
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
H molecule |
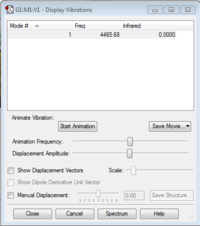
Vibrational Modes
Hydrogen only has one vibrational mode as it is a linear molecule and the IR value is zero as there is no absorption because there is no change in dipole moment.
Haber-Bosch Reaction Energies
| Energy | Energy value /a.u. |
|---|---|
| E(NH3) | -56.55776873 |
| 2*E(NH3) | -113.11553746 |
| E(N2) | -109.52412868 |
| E(H2) | -1.17853936 |
| 3*E(H2) | -3.53561808 |
| ΔE=2*E(NH3)-[E(N2)+3*E(H2)] | -0.05579070 |
| ΔE | -146.48 kJ/mol |
The energy for the reaction is negative therefore the Ammonia product is more stable than the reactants as it is lower in energy than the overall energy for Hydrogen and Nitrogen.
N2 Molecular Orbitals
-
Molecular orbital 1 shows the MO formed from the overlap of the 2py or 2pz AOs.
-
Molecular orbital 2 shows the MO formed from the overlap of the 2px AOs.
-
Molecular orbital 3 shows the anti-bonding MO formed from the overlap of the 2py or 2pz AOs.
-
Molecular orbital 3 shows the anti-bonding MO formed from the overlap of the 2px AOs.
CN-
Properties

| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | -1 |
| Final energy E(RB3LYP) | -92.82453153 a.u. |
| RMS Gradient | 0.00000704 |
| Point Group | C*V |
| Optimised CN bond length | 1.18409 Å |
| Optimised CN bond angle | 180° |
"Item" table from log file:
Item Value Threshold Converged? Maximum Force 0.000012 0.000450 YES RMS Force 0.000012 0.000300 YES Maximum Displacement 0.000005 0.001800 YES RMS Displacement 0.000008 0.001200 YES
CN molecule |
Vibrational Modes
Using the 3N-5 rule we would expect 1 vibrational mode for CN- as there are 2 atoms. The vibrational mode is a "bond stretch" vibration. As CN- has a dipole moment there will be a change in dipole moment during this stretch, thus the molecule will absorb IR radiation. One band would be expected to be seen in an experimental spectrum of gaseous CN- as there is only one distinct vibrational frequency at which CN- absorbs EM radiation.
Charge Analysis

The image on the right shows the charge distribution found on CN- for the different atoms. It would be expected for the Nitrogen atom to have the more negative charge as it is the more electronegative atom and so will pull more of the electron density towards itself. Carbon will also have a negative charge as the whole molecule has a single negative charge, just less negative than Nitrogen.
Molecular Orbitals
-
Molecular orbital 1 is occupied and shows the 2σ bonding MO formed by the overlap of the N 2s AO with the C 2s AO. The orbital is shifted towards Nitrogen due to Nitrogen's higher electron density.
-
Molecular orbital 2 is occupied and shows the 2σ* anti-bonding MO formed by the overlap of the N 2s AO with the C 2s AO. The anti-bonding orbital around Carbon is larger as it is the more electropositive atom.
-
Molecular orbital 3 is occupied and shows the 1π bonding MO formed by the overlap of the N 2p AO with the C 2p AO.
-
Molecular orbital 4 is the HOMO and shows the 3σ bonding MO formed by the overlap of the N 2p AO with the C 2p AO.
-
Molecular orbital 5 is the LUMO and shows the 1π* anti-bonding MO formed by the overlap of the N 2p AO with the C 2p AO.
H2SiO
Properties

| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final energy E(RB3LYP) | -365.90001403 a.u. |
| RMS Gradient | 0.00000941 |
| Point Group | C2V |
| Optimised Si=O bond length | 1.53172 Å |
| Optimised H-Si=O bond angle | 124.2° |
| Optimised Si-H bond length | 1.48652 Å |
| Optimised H-Si-H bond angle | 111.7° |
"Item" table from log file:
Item Value Threshold Converged? Maximum Force 0.000023 0.000450 YES RMS Force 0.000009 0.000300 YES Maximum Displacement 0.000022 0.001800 YES RMS Displacement 0.000015 0.001200 YES
HSiO molecule |
Vibrational Modes

Using the 3N-6 rule we would expect 6 vibrational modes for H2SiO as there are 4 atoms. No modes are degenerate as none have the same frequency and IR number so, therefore, none will have the same energy. Modes 1, 2, and 3 are "bending" vibrations whereas modes 5 and 6 are "bond stretch" vibrations. Mode 4 is a mix of "bending" and "bond stretch" vibrations, where the Si=O bond stretches and the Si-H bonds bend. 6 bands would be expected to be seen in an experimental spectrum of gaseous H2SiO as there are 6 distinct vibrational frequencies at which H2SiO absorbs EM radiation, as none of the 6 modes are degenerate.
Charge Analysis

The image shows the charge distribution found on H2SiO for the different atoms. It would be expected for the Oxygen atom to have a negative charge as it is the more electronegative atom and so will pull more of the electron density towards itself, and therefore the Silicon and Hydrogen atoms would be expected to have more positive charges than the Oxygen.
References
- ↑ CRC Handbook of Chemistry and Physics, 94th ed. http://www.hbcpnetbase.com. Page 9-26.Retrieved 18 June 2013. via https://en.wikipedia.org/wiki/Ammonia_(data_page)
- ↑ CRC Handbook of Chemistry and Physics, 94th ed. http://www.hbcpnetbase.com. Page 9-26.Retrieved 18 June 2013. via https://en.wikipedia.org/wiki/Ammonia_(data_page)
- ↑ Huheey, pps. A-21 to A-34; T.L. Cottrell, "The Strengths of Chemical Bonds," 2nd ed., Butterworths, London, 1958; B. deB. Darwent, "National Standard Reference Data Series," National Bureau of Standards, No. 31, Washington, DC, 1970; S.W. Benson, J. Chem. Educ., 42, 502 (1965).
- ↑ Huheey, pps. A-21 to A-34; T.L. Cottrell, "The Strengths of Chemical Bonds," 2nd ed., Butterworths, London, 1958; B. deB. Darwent, "National Standard Reference Data Series," National Bureau of Standards, No. 31, Washington, DC, 1970; S.W. Benson, J. Chem. Educ., 42, 502 (1965).