Thermal expansion of MgO

Introduction

Aim

The aim of this computational lab is to monitor the thermal expansion of the MgO crystal lattice. The General Utility Lattice program (GULP) is used to find the vibrational energy modes and the Helmholtz free energy of the MgO crystal. This in turn is used to calculate the lattice constants and volume of the MgO lattice which can be used to monitor the thermal expansion of the lattice. Using these calculations the coefficient of thermal expansion is found.

Quasi-Harmonic model and Molecular Dynamics model

The thermal expansion of the MgO crystal is modeled using two models; the quasi harmonic model and the molecular dynamics model.

Thermal expansion is the change in dimensions of a crystal that occurs with a change in temperature.

The harmonic potential model would fail in explaining thermal expansion, as the equilibrium distance between atoms does not change with temperature. However the quasi harmonic approximation is a phonon-based model in which the frequencies are dependent on the volume in order to account for the thermal effects. The parabolic potential of the harmonic potential is shifted at different Helmholtz free energies at varying temperatures. Therefore the optimal bond length is changed with temperature corresponding to the expansion of the crystal.

The equation that gives the relationship between the vibrational states and the wave vectors, k in a 1D chain is:

$ω_{k} = \sqrt{\frac{4 J}{M}} s i n (\frac{k a}{2})$

As the MgO crystal lattice is periodic, it can be described as a fourier series. There is a wave vector, k for every possible vibration of the crystal. By summing of all the wave vectors which is also the vibrational modes of the crystal, the free energy of the quasi harmonic approximation is calculated. The free energy of the crystal is given by:

$F = E_{0} + \frac{1}{2} \sum_{k, j} ℏ ω_{j, k} + K_{B} T \sum_{k, j} l n [1 - e x p (- \frac{ℏ ω_{j, k}}{K_{B} T})]$

The volume that minimizes the Helmholtz free energy is found for each temperature. The changing optimum volume as the temperature changes monitors the thermal expansion.

In the molecular dynamics model, classical mechanics is used. Newton's laws of motions are applied to the atoms in the lattice structure to compute the positions of the atoms at designated time intervals. Hence the model is able to measure the lattice parameters and volumes of the atoms at regular time intervals at a given temperature. It is assumed that the atoms interact by an anharmonic potential.

Thermal expansion coefficient

The coefficient of thermal expansion measures the factional change in size per degree change in temperature at a constant pressure. We can assume that pressure is constant since we are interested in a solid.

The coefficient of thermal expansion, $α$ can be found using the equation:

$α = \frac{1}{V_{0}} {(\frac{\partial V}{\partial T})}_{p}$

$V_{0}$ is the volume at 0K. $T$ is the temperature. $\frac{\partial V}{\partial T}$ is the change in volume with respect to the temperature. The subscript p shows that the system is help under constant pressure when the simulations are run.

The larger the thermal expansion coefficient, the faster the volume changes with the temperature.

Calculating the internal energy of an MgO crystal

molecule1
Figure 1: Conventional cell of MgO
molecule1
Figure 2: Primitive cell of MgO

The MgO lattice is a face-centered cubic structure (FCC).

The lattice can be represented conventionally as in figure 1. The lengths of the side of the face centered lattice is denoted $a_{c}$ , $b_{c}$ and $c_{c}$ where $a_{c} = b_{c} = c_{c}$ . The angle between $a_{c}$ and $b_{c}$ is $γ$ , the angle between $a_{c}$ and $c_{c}$ is $β$ and the angle between $b_{c}$ and $c_{c}$ is $α$ .

Although the MgO lattice can be described as a conventional cell it can be more simply looked at as a primitive cell as shown in figure 2. In the primitive cell $a_{p} = b_{p} = c_{p}$ and the $γ$ , $β$ , $α$ refer to the same angles as the conventional cell.

molecule1	molecule1
Figure 3	Figure 4

Figure 3 shows the vector forms as the primitive cell at initial state. Figure 6 shows the internal angles of the primitive cell at initial state.

The "binding energy" of the crystal which is the energy requried to pull the atoms apart to infinity was calculated to be -41.1 eV (3.s.f) which is equal to -3960 KJ/(mole unit cells) (3.s.f).

Lattice Vibrations - Computing the Phonons

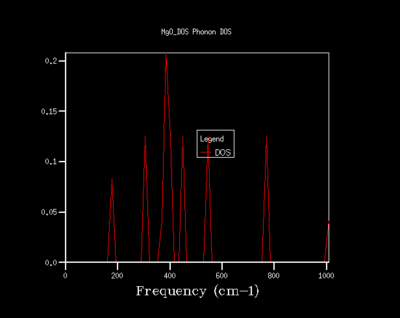
An appropriate Shrinking factor is needed before computing using the quasi harmonic model. The Density of states (DOS) gives the number of occupied and unoccupied vibrational states at each k-point. On figures 6 to 10 the density of states is plotted against the frequency at shrinking factors 1, 2, 4, 8, 16, 32 and 64 respectively. The shrinking factor represents the grid of k points. As the shrinking factor increases, the number of k-points computed increases hence the Density of state graph becomes smoother. This means that the as the shrinking factor increases, the information of the density of states becomes more detailed. The ideal shrinking factor needs to be balanced between the detail of the DOS and the time it takes for the simulation to run. This was determined to be a shrinkage factor of 32.

molecule1
Figure 5:

Figure 5 is the phonon dispersion curve. This shows the energy changes with each k-point.

molecule1	molecule1	molecule1
Figure 6: shrinking factor 1	Figure 7: shrinking factor 2	Figure 8: shrinking factor 4
molecule1	molecule1	molecule1
Figure 9: shrinking factor 8	Figure 10: shrinking factor 16	Figure 11: shrinking factor 32
molecule1
Figure 12: shrinking factor 64

The density of states graph for a shrinking factor of 1 corresponds to a single k-point. This DOS curve is the one that corresponds to the the dispersion curve on figure 5. The frequencies for the Density of States curve for a shrinking factor of 1 gives peaks at the frequencies around 290 cm^-1, 350 cm^-1, 690 cm^-1 and 805 cm^-1. This is the same as the symmetry point L on the dispersion curve.

The optimal grid size for MgO will be appropriate for calculations on other crystals with a similar cell structure to MgO such as CaO. The Zeolites will have a larger primitive cell in real space resulting in a smaller primitive cell in reciprocal space. This means that fewer k-points are needed to produce an accurate density of state graph and hence the shrinking factor required will also be smaller. Lithium is a metallic structure with a delocalised sea of electrons between the positively charge metal ions. Due to these electrostatic forces between the electrons and the positive ions, vibrtaional energy levels do not fluctuate as much therefore, not as many K-points are needed in order to get an accurate density of state curve.

Calculating the Free Energy in the Harmonic Approximation

The Helmholtz Free energy was calculated for each shrinking factor.

molecule1
Figure 13: Table showing the free energies

The table on figure 13 shows the Helmholtz Free Energies calculated at different shrinking factors. As the Shrinking factor increases, the free energy becomes closer to the actual value. With a shrinking factor of 2 the free energy is accurate to 1 meV and 0.5 meV. From a shrinking factor of 4, the free energy is accurate to a value of 0.1 meV.

The Thermal Expansion of MgO

Quasi-Harmonic model

molecule1	molecule1
Figure 14: The Helmholtz free energy against temperature	Figure 15: The lattice constant against temperature

Figure 14 shows the plot of the Helmholtz free energy of MgO at different temperatures. Figure 15 shows the lattice constant of the MgO lattice plotted at different temperatures. It can be seen that the Helmholtz free energy decreases as the temperature increases and the lattice constant increases with increasing temperature. The reason behind this trend is that as the volume of the lattice increases the entropy will increase as well. As the entropy becomes more positive the Helmholtz free energy will become more negative. This can be deduced from the equation $A = U - T S$ , where $A$ is the helmholtz free energy, $U$ is the internal energy, $T$ is the temperature and $S$ is the entropy.

In a diatomic molecule with a harmonic potential the bond length will not increase with temperature. In the quasi-harmonic model the vibrational frequencies are dependent on the volume and the potential of the harmonic potential shifts according to the shift in Helmholtz free energy.

Physically, the thermal expansion occurs when the thermal energy is transformed into kinetic energy of the atoms in the MgO lattice. As more energy is given to the lattice structure, higher vibrational levels become accessible. The vibrational modes induced by higher vibrational levels cause more repulsive interactions with neighboring atoms causing an increase in bond length and hence an increase in volume.

In order to determine the coefficient of thermal expansion, a graph of volume against temperature is plotted.


Figure 16: Volume against temperature (Quasi-Harmonic) 100 to 1000 K	Figure 17: Volume against temperature (Quasi-Harmonic) 100 to 2500 K

There are a few approximations made in the calculation. The First assumption is that the nuclear and electronic wavefunctions can be separated also known as the Born-Oppenheimer approximation. The second assumption made is that there are no electron-electron interactions.

Molecular dynamics model

The molecular dynamics model allow all the atoms to move unpredictably with a certain velocity. Due to this unpredictability a larger cell is needed when carrying out the simulations. For this reason a supercell of 32 MgO units is used.

molecule1	molecule1
Figure 18: Volume against temperature (Molecular dynamics) 100 to 1000 K	Figure 19: Volume against temperature (Molecular dynamics) 100 to 2500 K

Figure 18 shows the results plotted by running the calculations under the molecular dynamics model.

Comparing the two models

molecule1
Figure 20: Volume against temperature (Molecular dynamics and Quasi-Harmonic)

Figure 20 shows the volume against temperature plot for both the quasi-harmonic model and the molecular dynamics model. The gradients of the two lines are slightly different which results in slightly different coefficients of thermal expansions for each model.

By comparing figure 16 and 17 it can be shown that the gradient of the line changes when the simulations take place at temperatures higher than 1000K in the quasi harmonic model. However, by comparing figures 18 and 19 it can be seen that the gradient does not change even when the simulations take place at higher temperatures in the molecular dynamics model.

This shows the limitations of using the quasi-harmonic model at temperatures that approach the melting point of MgO which is 2852 $\circ C$ . When the melting point is approached the lattice structure will start to break down and the phonon modes will not represent the actual motions of the ions as well. The reason for this is that the crystalline lattice breaks down into liquid. The breaking of bonds is not considered in the quasi harmonic model. Therefore the quasi harmonic model is a better approximation at lower temperatures.

The molecular dynamics model works well even when higher temperatures are approached. Although the molecular dynamic model will show limitations in representing the thermal expansion as an infinite number of MgO units is needed in order to find all the possible vibrations.

Thermal expansion coefficients

The equation $α = \frac{1}{V_{0}} {(\frac{\partial V}{\partial T})}_{p}$ is used to determine the coefficient of thermal expansion where the volume at 0K, $V_{0}$ is 18.680416 Angstroms. The table below shows the coefficients calculated:

	Coefficient of Thermal Expansion (K^-1)
Quasi Harmonic model	$2.68 \times 1 0^{- 5}$
Molecular dynamics model	$3.21 \times 1 0^{- 5}$

In literature ^[1] it shows that the coefficient of thermal expansion changes with temperature. The coefficient obtained from the quasi harmonic model is closer to the literature. Despite this both the coefficient of thermal expansion obtained from both models shows a fairly large discrepancy from the literature value. This can be due to the limitations discussed in the previously section.

Conclusion

The thermal expansion properties of MgO was investigated using two models; quasi harmonic and molecular dynamics model. The two models have different approaches to measuring the changing lattice parameters in the MgO lattice which in turn illustrates the expansion of the lattice.

It was found that the quasi harmonic model was a better approximation at lower temperatures. On the contrary, the molecular dynamics model produced more precise results at a larger range of temperatures. Nonetheless, both models had their limitations which explains the dependency in the coefficient of thermal expansion obtained and the literature.

References

↑ Robert R. Reeber, Kathryn Goessel, kai Wang, Eur. J. Mineral, 1995, 7, 1039-1047

[1] Robert R. Reeber, Kathryn Goessel, kai Wang, Eur. J. Mineral, 1995, 7, 1039-1047

[1]