Rep:Mod:MLBA1090 report
NH3, H2 and N2 optimization
NH3
The link to the opzimized .log Gaussian file can be found here
Optimization summary
optimized N-H bond distance = 1.01798 A
optimized H-N-H bond angles = 105.741 deg
| Molecule | NH3 |
| calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Final energy | -56.55776873 a.u. |
| RMS Gradient | 0.00000485 a.u. |
| point group | C3v |
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
optimized NH3 molecule |
vibrational analysis
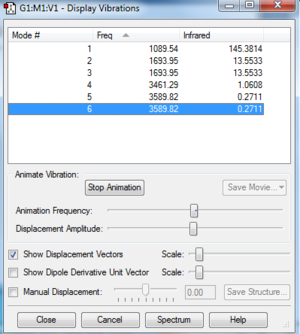
The number of vibrational modes calculated by Gaussian is the same as that predicted by the 3N-6 rule. Since there are 4 atoms in a molecule of ammonia, the expected number is 6 (3*4-6=6), which is exactly the same as in the number of modes in the window above, which is a screenshot of gaussian's output. We must keep in mind, though, that not all of these vibrational modes are have a unique zero point frequency. We can see that modes 2 and 3 are degenerate, as well as is true for 5 and 6. This means that not all of the vibrational modes would have a corresponding peak in the IR spectrum. The actual number of peaks would be 4, as the two degenerate pairs produce a single peak each only.
These vibrations correspond to different types of movement of the atoms within the molecule. Molecular bending motions are usually of lower energy, and therefore frequency, than molecular stretches. It is no different in this case, where the first three molecular vibrational modes (2 and 3 being degenerate) correspond to the scissoring and wagging motions. The latter three vibrations correspond to the symmetric stretch (4) and the asymmetric stretch (5 and 6). it is the first mode - the one with the wagging motion - which most resembles the motion of an umbrella.
charge analysis
Since nitrogen is widely known to be one of the most electronegative elements whereas the electronegativity of hydrogen is much smaller, it would be logical that nitrogen would attract the bonding electrons much more strongly. Thus, the expected result of the charge analysis would be a negative charge on the nitrogen and a positive charge on the hydrogens. Indeed, the analysis shows these results; the charge on the nitrogen is -1.125, whereas the charge on each of the three hydrogens is one third of the magnitude and positive (0.375). This is to be completely expected, as the overall charge must be 0, which means that each of the hydrogens who are all in the same position must contribute a third of the positive charge needed to neutralize the nitrogen's negative one.
H2
| Molecule | H2 |
| calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Final energy | -1.17853935 a.u. |
| RMS Gradient | 0.00003809 a.u. |
| point group | Dinf H |
Item Value Threshold Converged? Maximum Force 0.000066 0.000450 YES RMS Force 0.000066 0.000300 YES Maximum Displacement 0.000087 0.001800 YES RMS Displacement 0.000123 0.001200 YES
N2
summary: molecule - H2, calculation method - RB3LYP, Basis set - 6-31G(d,p), Final energy - -109.52412868 a.u., RMS Gradient - 0.00000134 a.u., point group - Dinf H
| Molecule | N2 |
| calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Final energy | -109.52412868 a.u. |
| RMS Gradient | 0.00000134 a.u. |
| point group | Dinf H |
Item Value Threshold Converged? Maximum Force 0.000002 0.000450 YES RMS Force 0.000002 0.000300 YES Maximum Displacement 0.000001 0.001800 YES RMS Displacement 0.000001 0.001200 YES
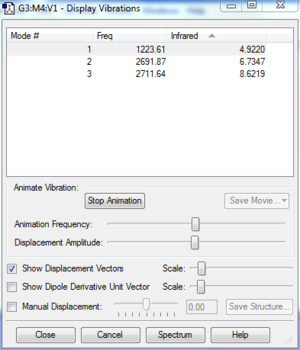
[[File:Vib_3_N2.PNG]|thumb|centre|figure 3:window showing the computed bibrational modes for nitrogen]
reaction enthalpy calculation
E(NH3)=-56.55776873 a.u. 2*E(NH3)=-113.115537 a.u. E(N2)=-109.52412868 a.u. E(H2)=-1.17853935 a.u. 3*E(H2)=-3.53561805 a.u. ΔE=2*E(NH3)-[E(N2)+3*E(H2)]=-0.05579095 a.u. ΔE=-146.479139 Kj/mol
H2S
Optimization results summary
| Molecule | H2S |
| calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Final energy | -399.39162414 a.u. |
| RMS Gradient | 0.00012068 a.u. |
| point group | C2v |
Item Value Threshold Converged? Maximum Force 0.000175 0.000450 YES RMS Force 0.000145 0.000300 YES Maximum Displacement 0.000465 0.001800 YES RMS Displacement 0.000390 0.001200 YES
vibrational states
There are three different vibrations available to the H2S molecule. This obeys the 3N-6 rule.
molecular charge diagram
As expected, the more electronegative sulfur will be the atom on which the negative charge resides. We can see that it is much less electronegative than nitrogen just by comparing the magnitude of the dipoles of H2S and NH3.
molecular orbitals
| orbital number | image of computed orbital | orbital energy (a.u.) | substituent AOs | type of orbital |
|---|---|---|---|---|
| 1 |  |
-0.74654 | 3s and two 1s | bonding |
| 2 |  |
-0.44963 | 3px and two 1s | bonding |
| 3 |  |
-0.36725 | 3py and two 1s | bonding |
| 4 |  |
-0.26181 | 3pz and two 1s | non-bonding, HOMO |
| 5 |  |
0.02126 | 3px and two 1s | anti-bonding, LUMO |
The above table shows the 5 molecular orbitals, which are ordered in increasing energy, and are all in or around the HOMO-LUMO energy level. The first four are all filled with electron pairs (fourth is HOMO) while the fifth is the LUMO. The first orbital is a bonding orbital made up of the 3s orbital of sulphur and the two 1s orbitals of hydrogen which combine in-phase. The following three orbitals are different combinations of the three 3p orbitals of sulphur and 1s orbitals of sulphur. They form two bonding orbitals, where the 3px and 3py combine with the 1s orbitals in phase. The third p ortbital, the 3pz is orthogonal to the other two and points away from the hydrogens, and so forms a non-bonding orbital, which is also the HOMO. The final orbital is a combination of two 1s orbitals of different phases combined out-of-phase with a 3px orbital, producing an anti-bonding orbital. The HOMO-LUMO transition is 0.28307a.u. which corresponds to 1.23411273408E-18 joules or 7.70270964611 eV. The bond order is difficult to assess, given that some of the molecular orbitals are mixtures of bonding and anti-bonding orbitals, but if we assume that one of the mixed orbitals is bonding and the other anti-bonding, we get a bond order of 2, which corresponds to the two signle bonds observed in a H2S molecule.