Rep:Mod:MJM333oooo
This examination of cycloadditions with computational calculations of varying complexity up to the B3LYP/6-31G* model chemistry includes the Diels-Alder cycloaddition between maleic anhydride and 1,3-cyclohexadiene and, following this, a [3+2] cycloaddition of a camphor-derived oxazoline N-oxide and a nitroalkene.
Cope rearrangement
Some background reading shows that "the B3LYP/6-31G* model chemistry" is the way that people often refer to this level of theory.[1]
Interesting.[1]
Drawing 1,5-hexadiene with an anti-periplanar linkage in the central four-carbon unit in ChemDraw Pro 13.0 then dragging the saved CDXML file into Avogadro to optimise the structure (MMFF94s force field), produced an anti-molecule ready for optimisation in Gaussian.
Drawing 1,5-hexadiene with a syn eclipsed linkage in the central four-carbon unit in ChemDraw then dragging the molecule, saved as a CDXML file, into Avogadro only produced the same approximately anti-periplanar conformer as before. Rotating one half of the molecule around the central bond allowed Avogadro to produce an optimised gauche-molecule (MMFF94s force field) for further optimisation in Gaussian. (The Avogadro files were imported by saving them as PDB files for opening in Gaussian.)
Optimisation of the structures (HF/3-21G) gave an anti-conformer with C2h symmetry, of energy -231.685 a.u. and a gauche-conformer with C2 symmetry of energy -231.691 a.u.. (Only a slight reorganisation of the molecules by Gaussian was seen, presumably because they were already optimised by Avogadro.)
Attempting to predict the lowest energy conformer, this gauche-diene with aligned pi-orbitals was optimised in Gaussian (HF/3-21G) to give this optimised structure of C2 symmerty with an energy of -231.692 a.u.. The pi-orbitals did not apparently stack or interact in any significant way. This was, however, not the intended structure.
Tweaking the dihedral angles a little to make the double bonds even more highly aligned together, submitting this gauche-diene to Gaussian for optimisation resulted in this new optimised strucure of C2 symmerty and low energy, -231.68871616 a.u.. The pi-orbitals appear to be interacting here, giving the energy stablisation looked for initially. This appears to be the lowest-energy conformation.
Ci symmetry
Optimising this initial guess at the HF/3-21G level of theory gave the anti-diene of Ci symmerty of energy -231.69253530 a.u.. Optimising again at the B3LYP/3-21G level gave this optimised structure of energy -233.33633685 a.u.. This is significantly lower in energy reflecting the higher level of theory used (although visual inspection shows the geometry little changed). Optimising again, this time at the B3LYP/6-31G level of theory, which took a little longer to calculate, gave this new optimised structure of energy -234.55970437 a.u.. This is again lower in energy, reflecting the higher level of theory's ability to get closer to the "true" minimum energy of the molecule. Again, visual inspection shows little change in overall geometry. Finally, using the drop-down menu box to specify a "d" additional to the 6-31G basis set, the B3LYP/6-31G* model chemistry produced a very similar optimised molecule this time with an energy of -234.61171038 (lower still).
Frequency caculations
Performing a frequency calculation at the B3LYP/6-31G level of theory gave no imaginary vibrational modes. The word "Thermochemistry" could not be found from View File under the Results menu... Trying again
Anti diene Ci B3LYP 6-31G STAR frequency 2c was the name of the last checkpont file worked with...
Optimising chair and boat transition structures
Chair form
Optimising a pair of allyl fragments at the HF/3-21G level of theory gave this structure of C2h symmerty. It has an imaginary frequency of -818.11 /cm.
Using the freezing technique, an imaginary frequency of -726.63 is initially obtained before improvement...
Boat form
Optimising using the QST2 method produced this C2v-symmerty transition state for the rearrangement of 1,5-hexadiene, having one imaginary frequency of -840.03 /cm. Clicking the picture of the transition state, below, shows it animated. One end of the molecule comes together as the other end separates: this appears to be the correct transition state.

Diels-Alder reaction
Moving on to plotting orbitals...
Butadiene
Optimising cis-butadiene at the AM1 level produced this HOMO: (anit-symmertic with respect to a mirror plane through the centre of the molecule)

and this LUMO: (symmetric with respect to the same mirror-plane)

Butadiene with ethene
With reactants and products based on the arrangement of atoms in norbornene (with the methylene in the smallest ring removed and replaced by hydrogens, as shown below)

optmised at the AM1 level of theory, this transition state was obtained, -0.01099615 a.u. in energy (a low value as might be expected for an electrocyclic reaction). It posessed one imaginary (negative) frequency at -52.77 /cm, shown below.

The imaginary frequency was a swivelling motion, not corresponding to the bonds lengthening and shortening in a Diels-Alder reaction. (Further optimising at the B3LYP/6-31* level of theory took quite a while, eventually failing.) Starting again with different starting structures...
Starting over again
Optimising cis-butadiene at the HF/3-21G level and then again at the B3LYP/6-31G* level gave a structure of energy -155.98595611 a.u.. Following the same two-step procedure for ethene gave a molecule of energy -78.58745827 a.u..
The two were placed next to each other in a likely reactive arrangement; the bond orders were changed to give that expected for cyclohexene, the product, to give a cyclohexene structure which was then partially optimised in Avogadro (MMFF94s model chemistry) to give this guess at the product structure (one that was not too far from the transition state itself). The reactants and product are shown below:

This transition state of energy -231.60320850 a.u. was obtained from this using the HF/3-21G model chemistry (TS(QST2) optimisation):

Repeating the transition state calculation at the B3LYP/6-31G* level of theory gave a transition state of energy -234.54389645 a.u. with this imaginary frequency at -525.11 /cm:

This is definitely the transition state corresponding to the Diels-Alder reaction, since the imaginary frequency corresponding to the "top" of the potential energy barrier here shows the bonds between the diene and the dienophile being made in a concerted fashion.
The transition state's HOMO:

and the transition state's LUMO:

are both symmetric with respect to a plane through the centre of the transition state.
Studying the Diels-Alder reaction's regioselectivity
Studying the Diels-Alder reaction by looking at the reaction of cyclohexa-1,3-diene and maleic anhydride.
Optimising the starting structures, at the B3LYP/6-31G* level of theory, it was found that a cyclohexadiene sturcture with a completely planar carbon backbone had a higher energy (-233.41588514 a.u.) than the structure with a pair of gauche methylene groups (-233.41893632 a.u.), giving the molecule a bit of a twist in its low-energy form.
Maleic anhydride, optimised at the B3LYP/6-31G* level of theory, and completely planar has an energy of -379.28954468 a.u.. Putting the anhydride and the hexadiene together in a way that matches the transition state of the Diels-Alder reaction studied previously (above)...
Endo transition state
The starting anhydride and the starting diene, both optimised at the B3LYP/6-31G* level of theory, were placed in close proximity as shown here; the bond orders were changed, with a pair of new bonds between the molecules with a pair of new bonds between the molecules as shown here; the resulting endo product geometry was optimised, for speed, in Avogadro (MMFF94s level), producing this structure and then optimised again at the B3LYP/6-31G* level of theory in Gaussian. The resulting optimised structure has an energy of -612.75829018 a.u. and possesses Cs symmerty, the twist seen in the original cyclohexadiene having become symmertical again. A mirror plane could be drawn down the centre of the molecule.
The reactants and product are shown below:

Calculating the transition state (TS(QST2), with the keyword "opt=noeigen") at the HF/3-21G level of theory gave this transition structure of energy -605.61036822 a.u. and with a single imaginary frequency of -643.49 /cm, indeed vibrating in a way confirming the transition state as that belonging to the Diels-Alder reaction (click the image below to animate).

Exo transition state
Following the same procedure for this exo pair:

produced a transition state of energy -605.60359124 a.u. and with one imaginary frequency of -647.52 /cm. The animation (click the image below to animate) is again in line with the correct Diels-Alder reaction.

The correct bonds are being formed in this transition state.
Comparison: exo or endo?
The HF/3-21G model chemistry shows the exo form of the transition state to be higher in energy than the endo form, suggesting that the endo product should be kinetically favoured. Looking at the molecular orbital picture, it is difficult to see why.
Endo HOMO:

Exo HOMO:

From the side, it is perhaps easier to see the electron density at the centre of the molecule.
Endo HOMO from the side:

Exo HOMO from the side:

There appears to be some orbital overlap between the anhydride group and the methylene carbons directly above them (as shown) in the exo form, suggesting stability of the transition state; in the endo transition state, on the other hand, there appears to be a non-bonding arrangement between the anhydride group and the molecule's central electron density above it (bordering on anti-bonding) suggesting relatively low stability. Why, then, should the endo transition state be lower in energy and therefore kinetically favoured?
Looking at the charge distribution in the transition states, shows that carbons on the side of the diene with the double bond are less negatively charged than the side with methylene carbons.
Endo charge distribution (below): the most negatively charged (methylene) carbons are not next to the most positively charged (anyhdride-group) carbons.

Exo charge distribution (below): this way round, the most positively charged carbons (belonging to the dienophile) are closely apposed to the most negatively charged carbons.

This may suggest that the molecule will more quickly react with the forming double bond away from the positively charged anhydride-group carbons.
A closer look: recalculating at the B3LYP/6-31G* level of theory
Recalculating (at around an hour for each calculation) the transition states at the B3LYP/6-31G* level of theory gave similar transition states with energies of -612.68339676 a.u. and -612.67931093 a.u. for the endo and exo forms respectively. Something useful is revealed at this (higher) level of theory:
The endo transition state HOMO orbital, below, now shows electron density around the central oxygen atom of the anhydride group, in-phase with the central electron density above it. This may be a clue that indeed this bonding interaction between the diene and dienophlie pi-systems is present in "real life" molecules (for which this model chemistry is an approximation).

The bonding interactions seen in the endo transition state, and refered to above, are closer together than the bonding interactons, refered to above, in the exo transition state (below), involving smaller lobes of electron density.

Experimental studies: Oxazoline N-oxides
Kouklovsky, Dirat, Berranger, Langlois, Tran-Huu-Dao and Riche (1998)[2] found that the reaction between the camphor-derived oxazoline N-oxide below,

and dipolarophile (1E)-1-Nitro-1-hexene,
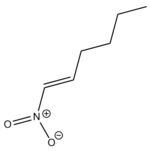
gave alomst exclusively the endo-regioisomer below:

The endo/exo selectivity was greater than 95:5. The regioselectivity was also greater than 95:5 (this figure refers to the ratio of the endo product above compared with the regioisomer below,

in which the nitro-group's position is reversed).
Computational studies relating to the reaction, carried out at the RHF/AM1 level, are discussed in a wonderful book by Gómez Gallego and Sierra (2004), used to explain the high selectivity of the reaction.[3]
Computational model
Optimising the structure of the camphor-derived oxazoline N-oxide in Gaussian at the HF/3-21G level of theory, and modeling the nitrohexene dipolarophlie as a truncated derivative, trans-1-nitropropene, also optimised in the same way, allows a look at the interacting HOMO and LUMO orbitals in these [3+2] cycloaddition reactants.
trans-1-nitropropene LUMO:

Camphor-derived oxazoline N-oxide HOMO:

Optimising again, this time at the B3LYP/6-31G* level, the camphor-derived oxazoline N-oxide HOMO, shown below, is clearly blocked from attack of the nitropropene dipolarophile from above by steric bulk.

The

Interestingly, the fronteir orbitals would also have the correct symmetry for a cycloaddition if the nitropropene fragment was placed the other way up, as to produce the endo-regioisomer seen at less than five percent.

The orbital contriution from the methyl group, however, is much lower than from the nitro group (the orbital on the m ethyl group is smaller than on the nitro group), explaining the regioselectivity? Replacing the methyl group with a butyl group to perhaps more closely simulate the experimental conditions, the LUMO orbitals change very little...

...but, of course, as shown now, the nitro-group would end up on the sterically hindered top face of the molecule! In the correct orientation for the nitro-group to end up on the least hindered bottom face of the molecule would require HOMO-LUMO orbital mismatch. These are both no-win situations: there is only really one correct alignment, the one that is seen experimentally.
Orbital energies at the B3LYP/6-31G* level
The orbital energies are, for the frontier orbitals:
Nitropropene dipolarophile HOMO: -0.28731 a.u. Nitropropene dipolarophile LUMO: -0.08602 a.u.
Oxazoline N-oxide dieneophile HOMO: -0.31720 a.u. Oxazoline N-oxide dieneophile LUMO: +0.14957 a.u.
HOMO-LUMO energy gaps
Dipolarophile HOMO - dieneophile LUMO gap: 0.43688 a.u.
Dipolarophile LUMO - dieneophile HOMO gap: 0.23118 a.u.
The narrower gap involves the LUMO of the dipolarophile (trans-1-nitropropene) and the HOMO of the dieneophlie (oxazoline N-oxide), so indeed the correct orbitals have been examined.[3]
References
- ↑ 1.0 1.1 Why the Standard B3LYP/6-31G* Model Chemistry Should Not Be Used in DFT Calculations of Molecular Thermochemistry: Understanding and Correcting the Problem, Kruse, H., Goerigk, L., Grimme, S., J. Org. Chem.; 2012; 77(23) pp 10824-10834; DOI:10.1021/jo302156p
- ↑ [3 + 2] Cycloadditions between α,β-Unsaturated Esters or Nitroalkenes and Camphor-Derived Oxazoline N-Oxides: Experimental and Theoretical Study, Kouklovsky, C., Dirat, O., Berranger, T., Langlois, Y., Tran-Huu-Dao, M. E., Riche, C. J., Org. Chem.; 1998; 63(15) pp 5123-5128; DOI:10.1021/jo980326e
- ↑ 3.0 3.1 Gómez Gallego, M., Miguel Ángel Sierra, M. A., Organic Reaction Mechanisms: 40 Solved Cases, Springer-Verlag, 2004, pp 101-106, ISBN 9783540003526, 3540003525
