Rep:Mod:MATTBIDWELL
Matthew Bidwell Synthesis and Computational Experiment 1C
In this Computational exercise we used the molecular modelling programs Avogadro and GaussView in order to investigate the molecular mechanics of cyclopentadiene and its hydrogenated products, conformational analysis of a key Taxol intermediate, NMR spectral simulation of another Taxol synthetic intermediate and the analysis of Shi and Jacobsen catalysts in their role in epoxidation reactions, focusing particularly on the transition states formed. Through these methods we teased out useful properties such as molecules geometry and regioselectivity and prediction of their 13C and 1H NMR spectra.
Cyclodimersation of Cyclopentadiene and Hydrogenation of Cyclopentadiene Dimer
Cyclodimersiation of Cyclopentadiene
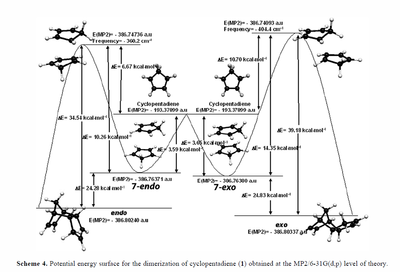
In the first part of the experiment we looked at the cyclodimerisation of cyclopentadiene and its subsequent hydrogenation, paying special attention to which of the endo or exo forms predominated and whether this is due to kinetic or thermodynamic reasons. The exo and endo structures were first optimised by calculation using MMFF94s force field and Conjugate Gradients algorithm in Avogadro in order to determine which product was thermodynamically more stable and so less energetically strained. Ab initio calculations would be more accurate however take longer to run computationally, therefore the use of the parametric method of Molecular Mechanics was used instead in this case. Through this analysis we were able to see which conformer had the largest energy contributions by considering total bond stretching energy, total angle bending energy, total torsional energy, total Van der Waals energy and total electrostatic energy of each molecule.
Comparing the relative stabilities of the endo and exo form of cyclopentadiene dimer, we can see that the exo conformer has a total energy which is almost 3 kcal/mol less than the endo form, therefore we can deduce that this is the thermodynamic product and that the endo conformer is the kinetic product. The biggest difference in energy lies in the total angle bending energy term which is the potential energy increase as bond angles are bent from their equilibrium position. We can also see that the non-bonded energy terms of the total Van der Waals and electrostatic energy, which are the pair wise sum of the of the energies of all possible interacting non-bonded atoms in the molecule, also contribute largely to the dicyclopentadiene's total energy. Interestingly we can also see that the total torsional energy of the molecules are negative which indicates that the value is insignificant and that it is due to noise rather than a chemical interaction as the torsion energy term in molecular mechanics is primarily used to correct the remaining energy terms rather than to represent an actual physical process.
Diels Alder Cycloaddition
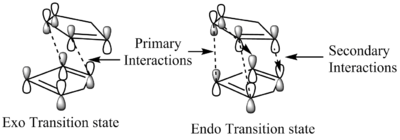
The Diels Alder reaction occuring is a concerted π4s + π2s thermal bicyclic cycloaddition which involves the sigma-overlap of the diene (in s-cis conformation) and the dienophile (usually electron poor), yielding stereospecific exo and endo products, due to the fact reactants may approach each other in two distinct orientations.[1] Normally in such reactions the endo product dominates, but as we can see from the table below the exo conformer is the most stable as previously discussed. This seems to be counter-intuitive at first glance however we must examine the transition states of the two conformers to find a satisfactory answer. At room temperature it is the endo molecule that dominates due to the fact the reaction is under kinetic control and the transition state energy of the endo dimer is lower than that of the exo dimer by 4.54 kcal/mol.[2] Woodward and Hoffmann ascribed preferential endo formation to the stabilising interaction of the occupied and unoccupied frontier orbitals(HOMO-LUMO orbitals) being favoured by orbital symmetry in the endo over the exo conformation.[3] From the diagram below we can see the primary Frontier Molecular orbital interactions as solid lines, while the secondary interactions are dashed lines, it is suggested that it is these secondary interactions that are responsible for the added stabilisation of the endo conformer however this is under debate as the cyclopentadiene rings may not approach close enough for interactions to occur.

| Dimer | Total bond stretching energy (kcal/mol) | Total angle bending energy (kcal/mol) | Total torsional energy (kcal/mol) | Total van der Waals energy (kcal/mol) | Total electrostatic energy (kcal/mol) | Total energy (kcal/mol) |
|---|---|---|---|---|---|---|
| Dimer 1 exo | 3.54294 | 30.77280 | -2.73100 | 12.80150 | 13.01367 | 55.37344 |
| Dimer 2 endo | 3.46737 | 33.19135 | -2.94947 | 12.35735 | 14.18428 | 58.19069 |
Bredt's rule and Bridgehead double bonds
Bredt's rule is an empirical observation that states a double bond can't be placed at a bridgehead position unless the ring is large enough to accommodate it. This observation is the consequence of the fact that having a double bond at a bridgehead is equivalent to having a trans double bond on a ring, which is not possible due to ring and angle strain in the ring. Therefore the p orbitals of the bridgehead carbon and adjacent atoms are orthogonal and so unable to align properly to form a pi bond.[5] The rule is useful for predicting the elimination product of a bridged ring system and also helps to explain the the stability of the double bond at non bridgehead carbons in a bridged ring system such as norbornene.
Hydrogenation of Endo Cyclpentadiene Dimer
The endo conformer previously seen can be partially hydrogenated to form Molecule 3 and 4. To see which molecule is preferentially formed the molecules' structures were optimised in Avogadro using MMFF94s Force Field and Conjugate Fields algorithm, and the thermodynamic product was found.
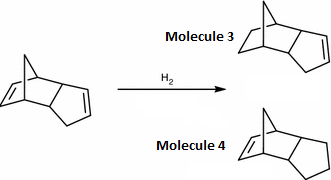
The data above shows that molecule 4 is the most stable and therefore is the product, as the reaction is under thermodynamic control. Molecule 3 has a much larger angle bending energy term than molecule 4 and this could be due to the fact that molecule 3 has a sp2 carbon atom in a five membered ring rather than molecule 4 which has a double bond in the norbornene ring. This result is supported by literature which also suggests that steric factors play a role as well in the stereospecific reaction.[6]
The molecules, 9 and 10, analysed are synthetic intermediates of the drug Taxol and are atropisomers of each other. Atropisomers are stereoisomers resulting from hindered rotation about bonds, whose energy barriers are high enough such that separate isomers can be isolated.[7] In the paper published by Paquette[8] it is suggestd that the large barrier to rotation is due to the other functional groups on the ring, namely the fused cyclohexane ring adjacent which is unable to ring-flip. Our task is to find the lowest energy atropisomer of molecule 9 and 10 and see which of the conformations of each of the molecules cyclohexane ring yields the lowest energy molecule. It is expected that the chair conformer will be of the lowest energy in each case as it does not have any eclipsed bonds leading to unwanted 1,3 flagpole interactions such as in the boat conformer, and so should be the most stable.
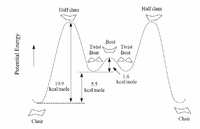
Avogardo was used to optimise the structures and find the minimum energy conformers, however this was not trivial as the optimisation by the Molecular Mechanics force field often found local minima in energy and significant physically manipulation of the structures were needed to find all of the conformers as shown below.
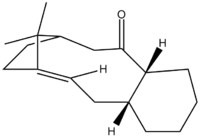
| Conformations of Taxol 9 Intermediate | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Taxol Indermediate C=O pointing up | Chair Conformer 1 | Boat Conformer | Twist Boat Conformer | Chair Conformer 2 | ||||||||
 |
||||||||||||
| Energy | kcal/mol | |||||||||||
| Total bond stretching energy (kcal/mol) | 7.72268 | 8.00296 | 7.94860 | 8.71590 | ||||||||
| Total angle bending energy (kcal/mol) | 28.32670 | 30.17441 | 29.50230 | 33.53171 | ||||||||
| Total torsional energy (kcal/mol) | 0.04734 | 2.73658 | 2.76679 | 3.11388 | ||||||||
| Total Van der Waals energy (kcal/mol) | 33.26454 | 35.79351 | 34.72044 | 35.89990 | ||||||||
| Total electrostatic energy (kcal/mol) | 0.29863 | 0.29255 | 0.31712 | 0.21803 | ||||||||
| Total energy (kcal/mol) | 70.56181 | 77.91101 | 76.28729 | 83.04830 | ||||||||
As expected, the chair conformer of molecule 9 is the most thermodynamically stable and has an overall energy approximately 7 kcal/mol lower than the boat conformer, due to unfavourable eclipsed bonds on 4 of the boat conformer carbon atoms, leading to repulsive 1,3 flagpole interactions as mentioned above. Strangely though the second chair conformer was found to be much higher in energy than any of the other conformers which may be due to unfavourable interactions caused by the strained sp2 carbonyl group, and this is shown through the large angle bending and Van der Waals energy term in the molecule.
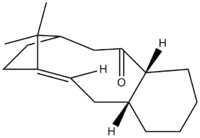
| Conformations of Taxol 10 Intermediate | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Taxol Indermediate C=O pointing down | Chair Conformer | Twist Boat Conformer 1 | Boat Conformer | Twist Boat Conformer 2 | ||||||||
 |
||||||||||||
| Energy | kcal/mol | |||||||||||
| Total bond stretching energy (kcal/mol) | 7.61050 | 7.69895 | 8.31672 | 8.67572 | ||||||||
| Total angle bending energy (kcal/mol) | 18.86745 | 19.56374 | 32.59590 | 25.77175 | ||||||||
| Total torsional energy (kcal/mol) | 0.25246 | 3.49010 | 4.31788 | 2.59024 | ||||||||
| Total Van der Waals energy (kcal/mol) | 33.17829 | 35.01708 | 35.19615 | 36.56469 | ||||||||
| Total electrostatic energy (kcal/mol) | -0.04935 | -0.05904 | -0.01859 | -0.10186 | ||||||||
| Total energy (kcal/mol) | 60.56229 | 66.53670 | 81.55812 | 74.36714 | ||||||||
As with molecule 9, the conformation with the lowest energy is the chair, with the boat conformer approximately 20 kcal/mol higher in energy, due to large angle bending and Van der Waals energy terms as discussed previously. It can be seen that molecule 10 is the thermodynamically most stable atropisomer and this can be explained by the large difference in angle bending energy in both molecule 9 and 10 chair conformers with a difference of 8 kcal/mol due to the less hindered down position of the sp2 carbonyl group.
Spectroscopic Simulation using Quantum Mechanics
The structures of the Taxol intermediate molecules 17 and 18 were given in the experimental guide and were sourced from the paper by Paquette.[8] These structures were drawn and their geomteries optimised in Avogardo using the MMFF94s mechanics force field as per previous examples. Particular care was taken to ensure the lowest energy geometries were found and that the hydrogen and methyl positions were correct throughout the optimisation to ensure a valid comparison to literature. After initial optimisation the molecules were saved as GaussView input files so that ab initio calculations could be performed in GaussView to further optimise and produce the carbon and hydrogen NMR spectra of the intermediates. Spin-spin coupling constant calculations were attempted however the time needed to compute the values was over 72 hours therefore it could not be completed within the time restrainsts set. The theory used was B3LYP from a 6-31G(d,p)basis set, specifing carefully the different solvation used in each NMR spectrum from literature so that valid comparison could be made.
| Conformations of Taxol 18 Intermediate | ||||||
|---|---|---|---|---|---|---|
| Taxol Indermediate C=O pointing down | Chair Conformer | Boat Conformer | ||||
 |
||||||
| Energy | kcal/mol | |||||
| Total bond stretching energy (kcal/mol) | 15.64881 | 14.39560 | ||||
| Total angle bending energy (kcal/mol) | 26.04977 | 27.80956 | ||||
| Total torsional energy (kcal/mol) | 17.43971 | 14.35119 | ||||
| Total Van der Waals energy (kcal/mol) | 52.46558 | 50.65077 | ||||
| Total electrostatic energy (kcal/mol) | -7.44276 | -6.45106 | ||||
| Total energy (kcal/mol) | 105.73760 | 102.24698 | ||||
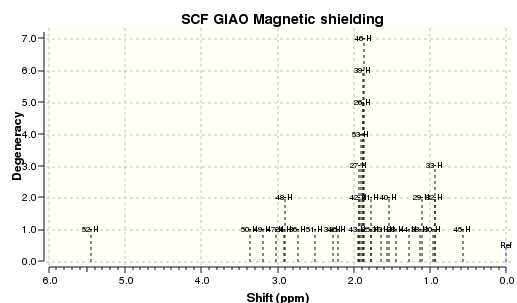
The Taxol 18 intermediate has two main conformers, counter-intuitively the thermodynamically favoured conformer is the boat conformer. However this result is reported in literature, as indeed the chair conformer predominates in the solid state, but in solution the boat conformer is preferred due to stabilising solvent affects.[10] The Taxol 17 intermediate also has a boat and chair conformer which can be seen below, and are higher in energy than the Taxol 18 molecule, therefore the NMR spectra are not shown but some values are compared for reference to deshielding effects.
| Atom Number | Calculated NMR peaks for Boat (ppm) | Calculated NMR peaks for Chair (ppm) |
|---|---|---|
| 52 | 5.36 | 5.45 |
| 50 | 3.33 | 3.37 |
| 49 | 3.09 | 3.19 |
| 47 | 3.03 | 3.02 |
| 24, 48 | 2.92 | 2.91 |
| 36 | 2.80 | 2.72 |
| 51 | 2.60 | 2.51 |
| 34 | 2.51 | 2.27 |
| 35 | 2.45 | 2.21 |
| 43, 42, 27, 53, 26, 39, 46 | 2.20 | 1.90 |
| 25, 41 | 2.07 | 1.77 |
| 37 | 1.96 | 1.64 |
| 31, 40 | 1.83 | 1.55 |
| 28 | 1.64 | 1.44 |
| 44 | 1.53 | 1.28 |
| 38, 29 | 1.39 | 1.11 |
| 30, 32, 33 | 1.17 | 0.94 |
| 45 | 1.01 | 0.57 |
| Speculated Atom Number | Reported 1H Shift (ppm) | Integration and Multiplicity |
|---|---|---|
| 52 | 5.21 | 1H, m |
| 50, 49, 47, 24, 48, 36 | 3.00-2.70 | 6H, m |
| 51, 34 | 2.70-2.35 | 4H, m |
| 35, 43, 42, 27, 53, 26, 39, 46, 25, 41 | 2.20-1.70 | 6H, m |
| 37, 31, 40 | 1.58 | 1H, t |
| 28, 44 | 1.50-1.20 | 3H, m |
| 38, 29 | 1.10 | 3H, s |
| 30, 32, 33 | 1.07 | 3H, s |
| 45 | 1.03 | 3H, s |
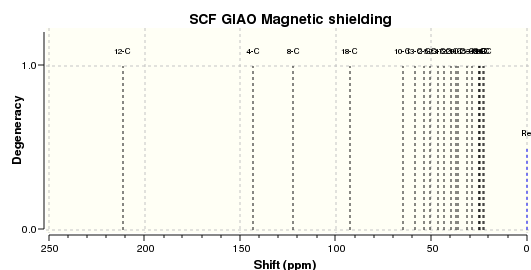
| Atom Number | Calculated NMR peaks for Boat (ppm)[11] | Calculated NMR peaks for Chair (ppm)[12] | Literature values (ppm)[13] |
|---|---|---|---|
| 12 | 211.0 | 211.3 | 211.5 |
| 4 | 148.6 | 143.4 | 148.7 |
| 8 | 118.6 | 122.2 | 120.9 |
| 10 | 88.7 | 92.7 | 74.6 |
| 13 | 67.5 | 65.1 | 60.5 |
| 2 | 55.4 | 54.0 | 51.3 |
| 5 | 49.9 | 50.5 | 50.9 |
| 23 | 46.6 | 46.4 | 45.5 |
| 17 | 44.3 | 43.5 | 40.8 |
| 22 | 41.2 | 39.5 | 38.7 |
| 9 | 37.4 | 36.9 | 36.8 |
| 11 | 36.2 | 36.3 | 35.5 |
| 15 | 32.0 | 31.5 | 30.00 |
| 3 | 29.1 | 28.6 | 25.6 |
| 19 | 28.6 | 25.2 | 25.4 |
| 7 | 25.8 | 25.0 | 22.2 |
| 1 | 25.1 | 24.4 | 21.4 |
| 16 | 21.7 | 22.6 | 19.83 |
| Conformations of Taxol 17 Intermediate | ||||||
|---|---|---|---|---|---|---|
| Taxol Indermediate C=O pointing up | Chair Conformer | Boat Conformer | ||||
 |
||||||
| Energy | kcal/mol | |||||
| Total bond stretching energy (kcal/mol) | 15.96706 | 15.97311 | ||||
| Total angle bending energy (kcal/mol) | 31.34441 | 31.22036 | ||||
| Total torsional energy (kcal/mol) | 11.17509 | 13.52954 | ||||
| Total Van der Waals energy (kcal/mol) | 52.12292 | 53.84688 | ||||
| Total electrostatic energy (kcal/mol) | -7.37665 | -7.03158 | ||||
| Total energy (kcal/mol) | 104.73795 | 109.12670 | ||||
Taxol 18 NMR Statistical Comparison
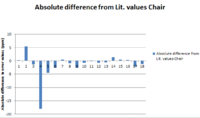
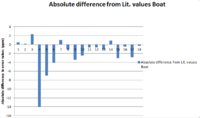
In order to evaluate the calculated data properly a statistical comparison to the literature is needed in order to work out the associated errors. Unfortunately it is only possible to analyse the 13C NMR data as the 1H NMR literature data is not detailed enough to compare with directly, a different possibly more relevent source would be needed for this. At first I wanted to apply a confidence test on the 13C NMR data in order to determine if there were any outliers in the data, however we only have two distinct data points for each reference value so this was not possible as a sample size of at least 30 would be needed for a meaningful test. Therefore instead I compared the absolute errors from the literature values for the chair and boat conformers and also calculated was the linear regression of each data set with respect to the literature values.
The Chair conformer has a very high R-squared value, but has a slightly larger deviance in chemical shift values from literature (which may be hard to see in the graph as the scales of the bar charts are slightly different). This in line with the theory that the boat conformer is slightly more favourable than the chair conformer in soltion for molecule 18.

The Boat conformer also has a very high R-squared value which shows good correlation with literature, and has less deviation from literature chemical shift as seen the in the bar chart above.

Analysis of the properties of the synthesised alkene epoxides
Crystal Structures of Jacobsen and Shi Catalysts
Shi Catalyst
| Carbon environment | C-O bond length (Angstroms) |
|---|---|
| Acetal ring 1 first bond | 1.423 |
| Acetal ring 1 second bond | 1.454 |
| Pyranose ring first bond | 1.415 |
| Pyranose ring second bond | 1.423 |
| Acetal ring 2 first bond | 1.428 |
| Acetal ring 2 second bond | 1.454 |
Firstly the crystal structure of the Shi catalyst was searched for in the Cambridge Structural Database using the program Conquest and the most revised and up to date crystal structure was chosen from the resulting search to ensure the most accurate analysis could be performed. After importing the resulting crystal structure into the program Mercury the C-O bond lengths of the 3 anomeric centres were determined and subsequently analysed. Differing bond lengths in the anomeric centres were seen in the 6-membered pyranose ring and the 5-membered acetal like rings as shown in the table below:
| Carbon environment | C-O bond length (Angstroms) |
|---|---|
| Acetal ring 1 first bond | 1.423 |
| Acetal ring 1 second bond | 1.454 |
| Pyranose ring first bond | 1.415 |
| Pyranose ring second bond | 1.423 |
| Acetal ring 2 first bond | 1.428 |
| Acetal ring 2 second bond | 1.454 |
At first glance at the table above it becomes apparent that the C-O bond lengths are larger in the acetal rings than in the pyranose ring. Mercury calculates the pyranose C-O bond lengths to be 1.415 and 1.423 Angstroms; this increase in bond length suggests a weaker bond and so a larger contrbution of stereoelctronic effects leading to donation of the lone pair on the oxygen atom into the σ* C-O orbital, which also in turns leads to larger C-O-C bond angles. While in the acetal rings the C-O bond is even longer, 1.42-1.43 and 1.454 Angstroms, which suggests a greater overlap of the oxygen lone pair orbital with the σ* C-O orbitals to give larger stereoelectronic interactions and so even weaker bonds.
Jacobsen Catalyst
As above the crystal structure of the Jacobsen catalyst was searched for in the Cambridge structural database, and the most optimised, up to date structure was chosen in Conquest and then analysed in Mercury. By looking at Jacobsen's catalyst it can be seen that there will be many unfavourable interactions due to the tert-butyl groups, however suprisingly not all of the interactions are repulsive. If the sum of the Van der Waals radii for the approach of two hydrogen atoms is 2.4 Angstroms or greater than the interaction is attractive, however below this it becomes severly repulsive, and this can be likened to the Lennard-Jones potential for two approaching atoms.
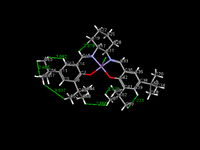
As seen in the picture above there are a few favourable H-H Van der Waals interactions between the tert-butyl groups, however these attractive forces are overshadowed by repulsive steric clashes such as of the two terminal tert-butyl groups which are ortho to the lone hydrogen on the benzene ring at the open face, which are less than the Van der Waals radius apart at 2.223 Angstroms away. There are many other such repulsive interactions also present as well.
Epoxide Formation
Firstly the two epoxides chosen, Trans-stilbene oxide and Styrene oxide were optimised in Avogadro using the MMFF94s force field and Conjugate Gradients algorithm. Subsequently the molecules were further optimised in Gaussview using B3LYP theory and 6-31G(d,p) basis set and their NMR spectra were calculated. The calculation of the coupling constants for each epoxide were also attempted, however the calculation took far too long to run and so was not possible.
Styrene Oxide
Below is the thermodynamic data of styrene oxide molecule, the lowest energy conformer was found to be when the ring was almost perpendicular to the epoxide centre in order to minimise unfavourable steric clashes. This allows us to compute an NMR spectrum with values close to the literature data.
| Styrene Oxide energy contributions | ||||
|---|---|---|---|---|
| Styrene Oxide | Styrene oxide J mol | |||
 |
||||
| Energy | kcal/mol | |||
| Total bond stretching energy (kcal/mol) | 1.84035 | |||
| Total angle bending energy (kcal/mol) | 1.42443 | |||
| Total torsional energy (kcal/mol) | 2.34617 | |||
| Total Van der Waals energy (kcal/mol) | 13.66548 | |||
| Total electrostatic energy (kcal/mol) | 3.08323 | |||
| Total energy (kcal/mol) | 21.61527 | |||
NMR of Styrene Oxide
| Atom Number | Calculated 1H Shift (ppm)[14] | Literature value (ppm)[15] |
|---|---|---|
| 8, 14, 10, 12 | 7.49 | 7.28-7.38, m |
| 16 | 7.30 | 7.28-7.38, m |
| 17 | 3.66 | 3.82, dd |
| 4 | 3.11 | 3.09, dd |
| 5 | 2.53 | 2.76, dd |
The computed 1H NMR values above match well with the literature values, however interestingly atom 16 does not have the same chemical shift as the other aromatic protons. This is due to the fact the computed NMR spectrum does not allow free rotation around a bond as discussed previously and so each atom has a specific 3D position. In this case the epoxide oxygen atom is having a Van der Waals interaction with the nearest aromatic proton, which causes this difference from the literature value.

| Atom Number | Calculated 13C Shift (ppm)[14] | Literature value (ppm)[16] |
|---|---|---|
| 6 | 135.1 | 137.6 |
| 13, 9 | 123.7 | 128.8 |
| 7,11 | 123.0 | 128.2 |
| 15 | 118.3 | 125.5 |
| 1 | 54.1 | 52.4 |
| 2 | 53.5 | 51.3 |
Considering the computed 13C NMR spectrum, the values also match the literature well but there are some differences which can be ascribed also to the lack of computational incorporation of free bond rotation, which doesn't enable us fully to distinguish which chemical shift belongs to which carbon atom as the same chemical environment here have different chemical shifts.

Trans-Stilbene
| Trans-Stilbene oxide energy contributions | ||||
|---|---|---|---|---|
| Trans-stilbene oxide | Trans-stilbene oxide J mol | |||
 |
||||
| Energy | kcal/mol | |||
| Total bond stretching energy (kcal/mol) | 3.72758 | |||
| Total angle bending energy (kcal/mol) | 2.69554 | |||
| Total torsional energy (kcal/mol) | 2.33107 | |||
| Total Van der Waals energy (kcal/mol) | 26.88686 | |||
| Total electrostatic energy (kcal/mol) | 5.35644 | |||
| Total energy (kcal/mol) | 39.45768 | |||
Trans-stilbene oxide NMR
| Atom Number | Calculated 1H Shift (ppm)[17] | Literature value (ppm)[18] |
|---|---|---|
| 8,24 | 7.57, 2H | 7.26-7.45, 10H, m |
| 18, 14, 20, 12, 10, 22, 26, 6 | 7.48, 8H | 7.26-7.45 |
| 27, 15 | 3.54, 2H | 3.86, 2H, s |
The 1H calculated NMR data matches well with the literature values reported, with only 0.3 ppm difference, which indicates that the correct conformation was optimised in Avogadro before the NMR spectra was calculated. However, as before with Styrene oxide the calculated chemical shifts for the aromatic protons are not averaged and so we have two chemical shifts at 7.57 and 7.48 ppm due to no rotation available around the aryl-carbon bond. Therefore a distinct 3D structure has been modeled and the epoxide oxygen has a definite position which interacts with the closest aromatic proton on each aryl ring leading to a deshielding effect and a higher proton shift of 7.57 ppm (2H) instead of 7.26-7.45 ppm (10H).

| Atom Number | Calculated 13C Shift (ppm)[17] | Literature value (ppm) [18] |
|---|---|---|
| 16, 4 | 134.1 | 137.0 |
| 7, 23 | 124.2 | 128.4 |
| 19, 11 | 123.5 | 128.4 |
| 9, 21 | 123.2 | 128.2 |
| 13, 17 | 123.1 | 128.2 |
| 5, 25 | 120.3 | 125.4 |
| 2, 1 | 66.4 | 62.81 |
The 13C calculated NMR matches reasonably well to literature, however as before there is no averaging of calculated NMR values for the same environment which makes it more difficult to assign peaks. I chose not to average the values myself as I felt this illustrates well that even though NMR prediction in GaussView is a powerful tool, it still has limitations. The ipso and para carbons are distinguished well but the ortho and meta carbons in the aromatic rings are seen to have different chemical shifts. The close match to literature value chemical shifts (less than 5 ppm on average) supports the assumption that the correct conformer was found.

Calculation and Comparison of Optical Rotations
The previously optimised epoxides which were used for NMR calculations were also used in the optical rotation calculations in GaussView. The same theory and basis sets were used as before B3YLP-6-31G(d,p)so that a valid comparison could be made. The calculations were then published to D-space after they had been performed.
With one exception the physical and chemical properties for enantiomers are indistinguishable in absence of other chiral materials, therefore the technique of optical rotation is very useful as enantiomers rotate the plane of polarised light in equal and opposite directions. Traditionally, optical polarimetry was performed using an instrument in which the extent of optical rotation was measured by the visual matching of splitting bands. Therefore the the D-line of the sodium lamp at the visible wavelength of 589nm was most often employed and so is still conventionally used.
Optical rotation comparison for Trans-Stilbene oxide
| Molecule | Calculated Optical Rotation (degrees) at 589 nm [19] | Literature value for Optical Rotation at 589 nm [20] |
|---|---|---|
| Trans-Stilbene oxide | 304.27 | 319.8 |
The optical rotation was only measured at 589 nm as this is the only wavelength at which literature data was reported, however the calculated optical rotation matches very well with literature and only differs by approximately 15 degrees which indicates that the the correct conformer was found, as a shift in the aryl ring plane of the molecule by only 10 degrees away from the correct orientation causes a discrepancy of 60 degrees or more in the calculated optical rotation value. Having said this, there are many differing literature values at the same wavelength and solvent system but they are all at different temperatures therefore it is not valid to compare these. From this value it is determined through comparison with literature that the (+)-(R,R)-trans-stilbene oxide enantiomer was modeled.
The ECD(Electronic Circular Dichroism) Spectrum, which in effect is the UV/Vis spectrum recorded with polarised light, is actually useless for the epoxides because no appropriate chromophore exists for them. However it was still calculated for Trans-stilbene oxide in order to show an example of the technique in the report.

Optical rotation comparison for Styrene oxide
| Molecule | Calculated Optical Rotation (degrees) at 589 nm[22] | Literature value for Optical Rotation at 589 nm [23] |
|---|---|---|
| Styrene oxide | -30.15 | -33.30 |
Similarly as above, the optical rotation was only measured at 589 nm as this is the only wavelength literature values were reported at. The calculated value for the optical rotation matches extremely well with the literature value and is less than 3 degrees different which indicates this is the same conformer as reported in the literature, which in this case is (R)-Styrene oxide.
Transition state for β-methyl styrene
The required energies of the Transition states were provided as it would be too time consuming in order to calculate them all.
Method of calculating Enantiomeric excess
The enantiomeric excess for the β-methyl styrene transition states using both Shi and Jacobsen catalysts can be found be examining the Gibbs free energy of the transition states provided to us in the output log files provided. By examining the lowest energy transition states of the S,S and R,R enantiomers it can be found which one predominates. Firstly the equilibrium constant must be found by using the below equation:
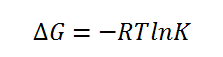
After this is done K can be subsequently split into the mole fraction contribution for each enantiomer (R,R and S,S):
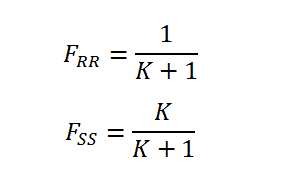
And thus the absolute difference between the mole fractions can be calculated F(R,R) - F(S,S) which equals the enantiomeric excess:
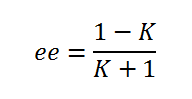
Shi Catlyst
| R,R Gibbs Free energy (Hartrees) | S,S Gibbs Free energy (Hartrees) | Δ Gibbs Free energy (Hartrees) | Δ Gibbs Free energy (J/mol) | K Equilibrium constant | Enantiomeric excess |
| -1343.02297 | -1343.017942 | -0.005028 | 13201.014 | 0.004867234 | 0.990312682 |
| -1343.019233 | -1343.017942 | -0.001291 | 3389.5205 | 0.25478958 | 0.593892739 |
| -1343.029272 | -1343.023766 | -0.005506 | 14456.003 | 0.002933713 | 0.994149736 |
| -1343.032443 | -1343.024742 | -0.007701 | 20218.9755 | 0.000286938 | 0.999426288 |
The two lowest energy transition states correspond to set 4 with (R,R)=-1343.032442 Hartrees and (S,S)=-1343.024742 Hartrees and are therefore the transition state which the Shi catalyst will most likely go through. The values in the table above were determined using the previous equations and we can see that the lowest energy transition states has an enantiomeric excess = 99.94% which infers that The (R,R) enantiomer is the one which is produced. If we compare this to the literature value[24] of 91.7%, this seems like a large value, however we must take into account different solvation systems, temperatures and other factors which may affect the values.
Jacobsen Catalyst
| Cis β methyl Styrene | ||||||
|---|---|---|---|---|---|---|
| S,R Gibbs Free energy (Hartrees) | R,S Gibbs Free energy (Hartrees) | Δ Gibbs Free energy (Hartrees) | Δ Gibbs Free energy (J/mol) | K Equilibrium constant | Enantiomeric excess | |
| -3383.259559 | -3383.25106 | 0.008499 | 22314.1245 | 0.000123235 | 0.99975356 | |
| -3383.253442 | -3383.25027 | 0.003172 | 8328.086 | 0.034752205 | 0.932829899 | |
The lowest energy transition state was found for Cis β methyl Styrene to be set 1 with (S,R)=-3383.259559 Hartrees and (R,S)=-3383.25106 Hartrees. The enantiomeric excess was calculated to be 99.98% which implies that the S,R enantiomer is the most favoured. Comparing this with the literature value[25] of 91% there is a quite good match, however the difference may be down to solvent and temperature effects as discussed above.
| Trans β methyl Styrene | ||||||
|---|---|---|---|---|---|---|
| S,S Gibbs Free energy (Hartrees) | R,R Gibbs Free energy (Hartrees) | Δ Gibbs Free energy (Hartrees) | Δ Gibbs Free energy (J/mol) | K Equilibrium constant | Enantiomeric excess | |
| -3383.262481 | -3383.253816 | 0.008665 | 22749.9575 | 0.000103366 | 0.999793288 | |
| -3383.257847 | -3383.254344 | 0.003503 | 9197.1265 | 0.024475583 | 0.952218318 | |
As above the lowest energy transition state found for Trans β methyl Styrene was set 1 with (S,S)=-3383.262481 Hartrees and (R,R)=-3383.253816 Hartress with an enantiomeric excess of 99.98%. Therefore this implies that the S,S enantiomer is the most favoured. Comparing this with the literature value[26] of 91-92% there is a good match but it may have differed as the literature value was ran using GC.
Overall Trans β methyl Styrene has a very slightly larger enantiomeric excess and so could be argued to be the preferred conformer however I believe there is not enough evidence to support this.
NCI Transition State Analysis
Non-Covalent Interactions play a central role in supramolecular chemistry and molecular biology, these interactions include hydrogen bonding, electrostatic effects and Van der Waals interactions to name a few. Attractive non-covalent interactions are important in catalysis as they act by lowerering the kinetic barriers to reactions through transition state stabilisation such as in the reaction of Jacobsen's catalyst with R-Styrene below:
Orbital |
The colours on the NCI surface above denote the strength of interactions, blue is very attractive, green mildly attractive, yellow mildly repulsive and red is strongly repulsive. We can see that there are strong attractive Van der Waals forces between the terminal tert-butyl groups which are helping to stabilise the transition state, the strong pi-stacking effect created by the aryl ring of the methyl stryrene and Jacobsen's catalyst also helps to stabilise the transition state, and is also present in protein folding and stacking of nucleobases in RNA and DNA. There are some repulsive interactions at the centre of the transition state, and this is due to the Mn atom clashing sterically with surrounding ligands.
QTAIM Analysis
QTAIM defines chemical bonding and structure of a chemical system based on the topology of the electron density in the transition state. BCP (bond critical points) are shown, and indicate where possible bonds may be formed in the transition state and are illustrated by solid lines, whereas dotted lines indicate regions where bonds may exist.

(R)-Styrene was chosen as for NCI analysis in order to compare the two methods. NCI gives far greater information about the transition state, as with QTAIM you cannot tell whether the interactions are attractive or repulsive, however in this case we can assume they are attractive after viewing the previous NCI surface and can see thatin this case many small attractive interactions are adding up to form one large overall one, stabilsing the transition state. As before it is possible to see the attractive forces between the tert-butyl groups and pi stacking effects of the aryl rings in the QTAIM image above.
Suggesting new candidates for investigations
First of all a reaxys substructure search was undertaken to find an epoxide with a molecular weight under 200 g/mol and an optical rotation above -300 and below +300 degrees. 1-phenyl-7-oxa-bicyclo[4.1.0]heptane was chosen as it is a small moelcule with a molecular weight of 174 g/mol and racemises when the equivalent alkene is epoxidised to form R,R and S,S enantiomers.
The R,R enantiomer has an optical rotation of 116 degrees[27], whereas the S,S enantiomer has an optical rotation of 92 degrees[28] in benzene. The molecule is also available to buy from Sigma-Aldrich if ever the optical rotations should want to be examined experimentally. It would be interesting to see if the literature values for the optical rotations matched the experimental values well.
References
- ↑ http://www.organic-chemistry.org/namedreactions/diels-alder-reaction.shtm.
- ↑ J. Org. Chem., 1994, 59 (4), pp 803–805
- ↑ The conservation of orbital symmetry. R. Hoffmann, R. B. Woodward Acc. Chem. Res. , 1968 , 1 , 17 - 22
- ↑ J. Mex. Chem. Soc. 2013 , 57(4) , 267-275
- ↑ Bredt, J. (1924). "Über sterische Hinderung in Brückenringen (Bredtsche Regel) und über die meso-trans-Stellung in kondensierten Ringsystemen des Hexamethylens". Justus Liebig's Annalen der Chemie 437 (1)DOI:10.1002/jlac.19244370102
- ↑ Shea, K. (1980). "Recent developments in the synthesis, structure and chemistry of bridgehead alkenes". Tetrahedron 36 (12): 1683–1715. DOI:10.1016/0040-4020(80)80067-6
- ↑ Bringmann G, Mortimer AJP, Keller PA, Gresser MJ, Garner J, Breuning M (2005). "Atroposelective Synthesis of Axially Chiral Biaryl Compounds". Angewandte Chemie International Edition 44 (34): 5384–5427
- ↑ 8.0 8.1 S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, 319 DOI:10.1016/S0040-4039(00)92617-0
- ↑ R. F. Daley, S. J. Daley, Organic Chemistry - Ch 3,2008, 143
- ↑ J. Org. Chem. , Vol . 70 , No . 26 , 2005 10728
- ↑ 11.0 11.1 Matthew Bidwell Taxol 18 Boat 1H NMR DOI:10042/27432
- ↑ 12.0 12.1 Matthew Bidwell Taxol 18 Chair 1H NMRDOI:10042/27435
- ↑ 13.0 13.1 L. A. Paquette, N. A. Pegg, D. Toops, G. D. Maynard, R. D. Rogers, J. Am. Chem. Soc.,1990, 112 (1), 277-83
- ↑ 14.0 14.1 Matthew Bidwell 1H NMR Styrene Oxide DOI:10042/27553
- ↑ http://www.hanhonggroup.com/nmr/nmr_en/RB03010019.html
- ↑ Shifting the equilibrium of a biocatalytic cascade synthesis to enantiopure epoxides using anion exchangers Joerg H. Schrittwieser, Iván Lavandera, Birgit Seisser, Barbara Mautner, Jeffrey H. Lutje Spelberg, Wolfgang Kroutil; Tetrahedron: Asymmetry, Volume 20, Issue 4, 11 March 2009, Pages 483–488
- ↑ 17.0 17.1 Matthew Bidwell Trans-Stilbene NMR CalculationsDOI:10042/27554
- ↑ 18.0 18.1 Org. Synth. 1997, 74, 91
- ↑ Matthew Bidwell Trans-Stilbene Optical rotationDOI:10042/27556
- ↑ Chen, Dajun; Nettles, Brian; Shi, Yian; Wang, Bin; Wong, O. Andrea; Wu, Xin-Yan; Zhao, Mei-Xin Journal of Organic Chemistry, 2009 , vol. 74, # 10 p. 3986 - 3989
- ↑ Matthew Bidwell ECD spectrum Trans-StilbeneDOI:10042/27557
- ↑ DOI:10042/27555
- ↑ Jensen; Kiskis Journal of the American Chemical Society, 1975 , vol. 97, p. 5825,5826
- ↑ J. Am. Chem. Soc. 1997, 119, 11224 - 11235
- ↑ Tian,H.;She,X.;Shu,L.;Yu,H.;Shi,Y.J. Am. Chem. Soc.200,122,11551
- ↑ Org. Synth. 2003, 80, 9
- ↑ Frohn, Michael; Shi, Yian; Tu, Yong; Wang, Zhi-Xian; Zhang, Jian-Rong Journal of the American Chemical Society, 1997 , vol. 119, # 46 p. 11224 - 11235
- ↑ Shi, Yian; Wang, Bin; Wong, O. Andrea; Zhao, Mei-Xin Journal of Organic Chemistry, 2009 , vol. 74, # 16 p. 6335 - 6338

