Rep:Mod:MAC01049979lab2
EX3
BH3 molecule
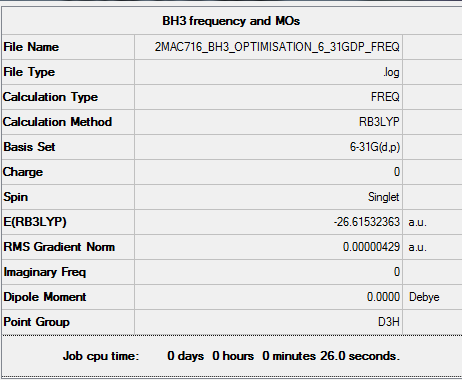
Method and basis set: RB3LYP, 6-31G(d,p)
Item table for optimisation
Item Value Threshold Converged?
Maximum Force 0.000009 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000034 0.001800 YES
RMS Displacement 0.000017 0.001200 YES
Predicted change in Energy=-4.343399D-10
Optimization completed.
-- Stationary point found.
Frequency analysis log file is here
Low frequency lines from log file
Low frequencies --- -2.2126 -1.0751 -0.0054 2.2359 10.2633 10.3194 Low frequencies --- 1162.9860 1213.1757 1213.1784
Jmol
BH3 molecule |
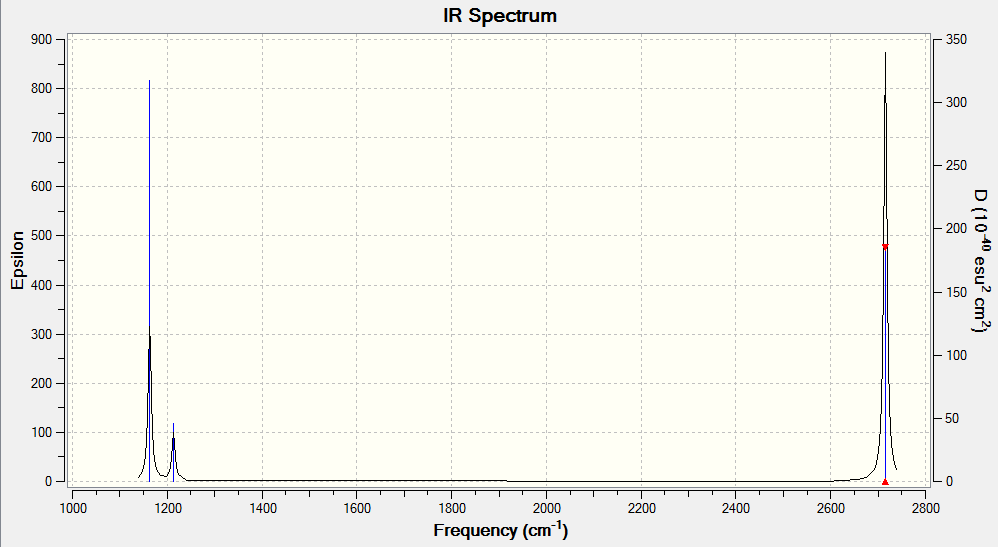
Vibration spectrum of BH3
| wavenumber (cm-1) | Intensity (arbitrary units) | Symmetry | IR active? | type |
|---|---|---|---|---|
| 1163 | 93 | A2 | yes | out-of-plane bend |
| 1213 | 14 | E | weak | bend |
| 1213 | 14 | E | weak | bend |
| 2582 | 0 | A1 | no | symmetric stretch |
| 2716 | 126 | E | yes | asymmetric stretch |
| 2716 | 126 | E | yes | asymmetric stretch |
From the formula, 3N-6, we expect (3) x (4)-6=6 vibrational modes for BH3 A total of 6 different vibrations are given in the table above. In order for a particular vibrational mode to be seen in the IR spectrum, it must be associated with a change in dipole moment. The symmetrical stretch vibration at 2582 cm-1 is not seen in the IR spectrum because this vibrational mode does not involve a change in the molecule's overall dipole moment when excited. The two bending modes at 1213 -1 are degenerate, ie have the same energy, and so they appear in the spectrum as a single peak. The two asymmetric stretches at 2716 cm-1 are also degenerate and hence appear as a single peak in the IR spectrum.
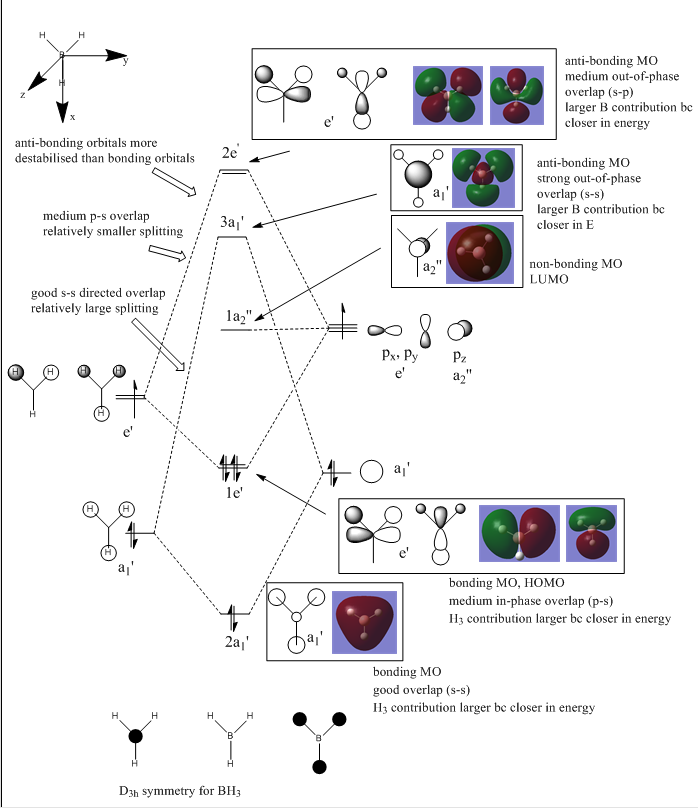
MO diagram for BH3
MO diagram for BH3 - adapted from Dr. Hunt, P.[1]
Are there any significant differences between the real MOs and the LCAO?
The real MOs calculated are very similar to those predicted by the LCAO combinations using the cartoon representations.
What does this say about the accuracy and usefulness of qualitative MO theory? This suggests that for BH3, the use of the LCAO method is very useful as it allows one to suggest an approximate structure of the real MOs. Just by considering the LCAOs, it is difficult to predict the relative energy of the 2e' and 3a1' anti-bonding MOS. The 2e' has strong directed s-s antibonding overlap while the 3a1' has medium s-p overlap. The energy difference between the two a1' fragment orbitals relative to the energy difference between the two e' fragment orbitals is not accurately known. Since the energy gap between the fragment orbitals affects the size of the energy splitting between the bonding and anti bonding pair, it is difficult to estimate the relative energy of the 2e' and 3a1' molecular orbitals from the LCAO method. Hence the quantitative calculation must be performed in order to determine relative positioning of these MOs.
Smf115 (talk) 18:06, 23 May 2018 (BST)Nicely adapted MO diagram and good consideration towards the energy estimation of the approaches. To improve, subtle differences in the shapes of 2e' and 3a1' MOs and the LCAOS, with larger contributions from H, should also be mentioned.
NH3
NH3 molecule
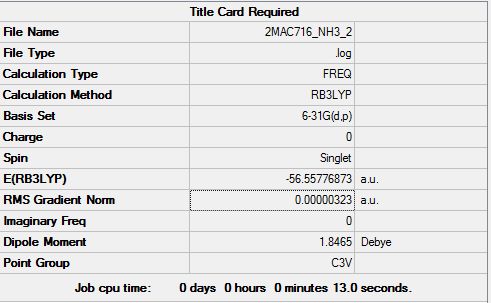
Method and basis set: RB3LYP, 6-31G(d,p)
Item table for optimisation
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000014 0.001800 YES
RMS Displacement 0.000009 0.001200 YES
Predicted change in Energy=-1.141602D-10
Optimization completed.
-- Stationary point found.
Frequency analysis
Frequency analysis log file is here
Low frequencies --- -0.0128 0.0008 0.0016 7.1032 8.1046 8.1049 Low frequencies --- 1089.3834 1693.9368 1693.9368
Jmol
NH3 molecule |
NH3BH3
Method and basis set: RB3LYP, 6-31G(d,p)
Item table for optimisation
Item Value Threshold Converged?
Maximum Force 0.000122 0.000450 YES
RMS Force 0.000058 0.000300 YES
Maximum Displacement 0.000513 0.001800 YES
RMS Displacement 0.000296 0.001200 YES
Predicted change in Energy=-1.631175D-07
Optimization completed.
-- Stationary point found.
Frequency analysis
Frequency analysis log file is here
Low frequencies --- 0.0013 0.0016 0.0017 16.8481 17.4133 37.2932 Low frequencies --- 265.8219 632.2116 639.3277
Jmol
NH3BH3 molecule |
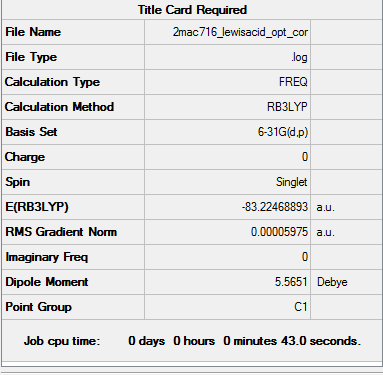
Calculation for the energy of the N-B dative bond
E(NH3)=-56.55777 a.u.
E(BH3)=-26.61532 a.u.
E(NH3BH3)=-83.22469 a.u.
Association energy:
ΔE=E(NH3BH3)-[E(NH3)+E(BH3)]=-83.22469-(-56.55777-26.61532)=-0.05160 a.u.
ΔE= 0.058 a.u./(3.8088x10-4 a.u. mol/ kJ)= -135 kJ/mol
This suggests that the bond energy of the B-N dative bond is approximately 135 kJ/mol.The B-N bond is isoelectronic with the C-C bond so we expect the bond energy for the B-N bond to be of the same magnitude as the C-C bond (348 kJ/mol). Relative to the C-C bond (348 kJ/mol) the B-N bond is relatively weak as it's bond energy is approximately half of that of the C-C bond.
Smf115 (talk) 18:03, 23 May 2018 (BST)Correct calcualtion method and a good comparison used to evaluate the result, however, literature values should be referenced.
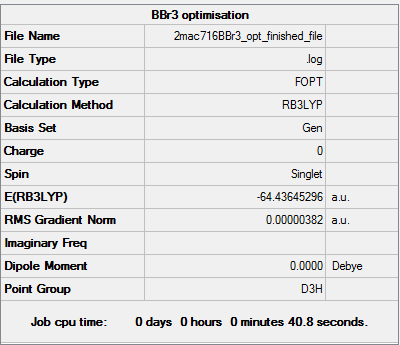
BBr3
Method and basis set RB3LYP, Gen: 6-31G(d,p) for B and PP LANL2DZ for Br
Item table for optimisation
Item Value Threshold Converged?
Maximum Force 0.000008 0.000450 YES
RMS Force 0.000005 0.000300 YES
Maximum Displacement 0.000036 0.001800 YES
RMS Displacement 0.000023 0.001200 YES
Predicted change in Energy=-4.026879D-10
Optimization completed.
-- Stationary point found.
DOI for optimisation
http://hdl.handle.net/10042/202376
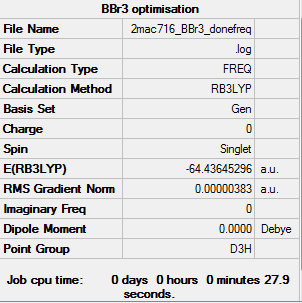
Frequency analysis
Summary Table:
Frequency analysis log file is here
Low frequencies --- -0.0137 -0.0064 -0.0046 2.4315 2.4315 4.8421 Low frequencies --- 155.9631 155.9651 267.7052
http://hdl.handle.net/10042/202379
Jmol
BBr3 molecule |
Project - Benzene
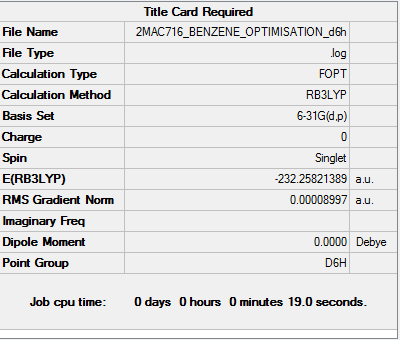
Benzene
Method and basis set: RB3LYP, 6-31G(d,p)
Item table for optimisation
Item Value Threshold Converged?
Maximum Force 0.000202 0.000450 YES
RMS Force 0.000078 0.000300 YES
Maximum Displacement 0.000823 0.001800 YES
RMS Displacement 0.000287 0.001200 YES
Predicted change in Energy=-4.347232D-07
Optimization completed.
-- Stationary point found.
Frequency analysis
Frequency analysis log file is here
Low frequencies --- -2.5530 -2.5530 -0.0088 -0.0042 -0.0041 10.3930 Low frequencies --- 413.9723 413.9723 621.1358
Jmol
Benzene molecule |
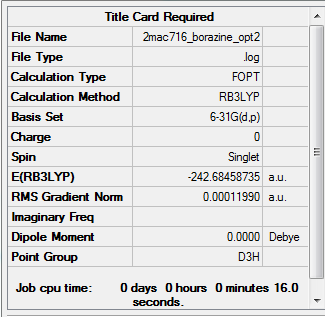
Borazine
Method and basis set: RB3LYP, 6-31G(d,p)
Item table for optimisation
Item Value Threshold Converged?
Maximum Force 0.000185 0.000450 YES
RMS Force 0.000057 0.000300 YES
Maximum Displacement 0.000449 0.001800 YES
RMS Displacement 0.000136 0.001200 YES
Predicted change in Energy=-3.059995D-07
Optimization completed.
-- Stationary point found.
Frequency analysis
Frequency analysis log file is here
Low frequencies --- -7.9285 -7.7974 -7.4289 -0.0096 0.0475 0.1134 Low frequencies --- 289.0304 289.0408 403.6933
Jmol
Borazine molecule |
Charge Analysis - Charge distribution for benzene and borazine
| Benzene |  |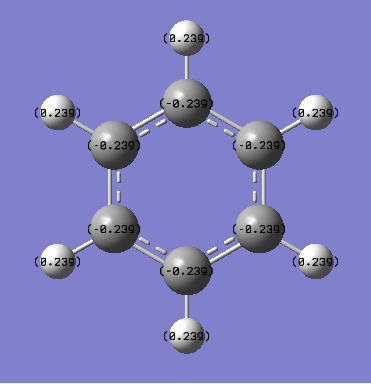
|
| Borazine |  |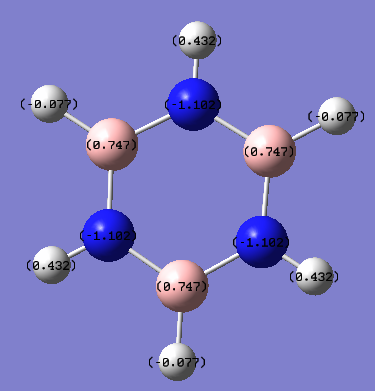
|
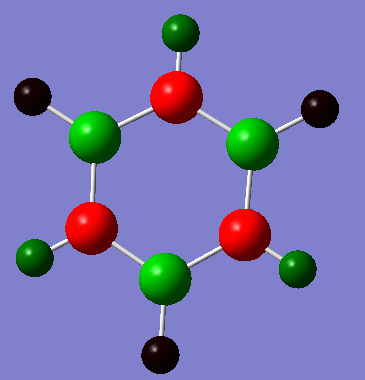
| Molecule | H (e) | B (e) | C (e) | N (e) |
|---|---|---|---|---|
| Benzene | +0.239 | - | -0.239 | - |
| Borazine | +0.432, -0.077 | +0.747 | - | -1.102 |
The charge distribution in borazine is much more polarised than the charge distribution in benzene. In the benzene molecule, the Hydrogen atoms all have the same positive partial charge(+0.234e) while the carbon atoms all have slightly more electron density and hence have a slightly negative partial charge (-0.234e) of the same magnitude (but opposite sign) as for the H atoms. This is as expected since C (Pauling electronegativity of 2.5) is slightly more electronegative than H (Pauling electronegativity of 2.1). Overall, the charge distribution is totally symmetric in benzene: all the C atoms have the same partial negative charge and all the H atoms have the same partial positive charge.
The charge distribution in Borazine is much more polarised. The boron atoms have a slight positive charge (0.747e) while the N atoms all have a partial negative charge (-1.102). The H atoms directly attached the the B atoms have a slight negative partial charge (-0.077e) while the those attached to the N atoms have a positive partial charge (+0.432e). The Pauling electronegativities of H, B and N are 2.1, 2.0 and 3.0 respectively. This suggests that B is the most electropositive atom in the molecule, and that it gives up electron density to both the N and the H atoms it is attached to and consequently has the greatest positive partial charge(+0.747e). This means that the H directly attached to the B atoms acquire electron density from B (since they are more slightly electronegative than B) and therefore have a slight negative partial charge(-0.077e). The N atoms acquire electron density from the H and B atoms directly attached to them and hence have a partial negative charge (-1.102). Finally, since N pulls electron density away from the H atoms directly attach to them this means that these H atoms have a slight positive charge (+0.432e). The B-N bond in borazine is more polarised relative to the B-H and N-H bonds since the electronegativity between B and N is the largest in the molecule (difference of 1.0 Pauling units). The N-H bond is the second most polarised bond since the electronegativity difference between N and H (0.9 Pauling units) is larger than that between B and H (0.1 Pauling units). Consequently, the B-H bond is the least polarised bond in the borazine molecule.
Comparison of MOs for Benzene and Borazine
| Benzene MO | Borazine MO | Analysis |
|---|---|---|
 |
 |
The two MOs for benzene and borazine are very similar in shape.Neither of the MOs involve the H atoms. The benzene MO shows p orbitals on each of the carbon atoms that are in the same plane as the benzene molecule all interacting in phase. Each given p orbital has a node which is centered on the each of the carbon atoms. However, these nodes are of lesser importance since they are centered directly on the atomic centers. The p-p head on sigma-type overlap between carbon atoms is relatively good and hence these interactions represent relatively strong sigma-type bonding interactions. Hence this is an overall strongly bonding MO.
The borazine MO is very similar in that there is good p-p head on overlap between the p orbitals in the plane of the molecule on the B and N atoms. Similarly to the benzene molecule, since there are nodes centered on each of the B and N atoms and the overall interaction is relatively good p-p head-on sigma type overlap, this MO also represents a strongly bonding MO. These MOs involve strong sigma-type interactions which contribute to them being lower in energy than the each of the two MOs below for benzene/borazine respectively. |
 |
 |
The two strongly bonding MOs for benzene and borazine are very similar in shape. The benzene MO involves relatively strong side-on overlap between the p orbitals that are perpendicular to the plane of the benzene molecule on each of the carbon atoms. This gives an pi-type bonding interaction between the C atoms which is delocalised over the center of the molecule but not over the H atoms. The H atom are not significantly involved in this MO. The nodes centered on each of the carbon atoms form a nodal plane in the plane of the molecule which represents a weak anti bonding interaction. Overall, the pi-type interactions suggest that this MO is a relatively strong bonding MO.
For the borazine MO, the p orbitals perpendicular to the plane of the molecule on the N and B atoms interact side-on in a relatively good pi-type interaction. The MO is very delocalised but does not involve the H atoms. The nodes on each of the B and N atoms form a nodal place in the plane of the borazine molecule that represents a weakly anti-bonding interaction. Overall this MO is therefore a relatively strong bonding MO. These MOs involve relatively good pi-type interactions and each respective MO is therefore slightly higher in energy than its corresponding MO above. |
 |
 |
These two MOs have a very similar shape. In the benzene MO, there are two pairs of carbon atoms interacting on opposite sides of the molecule. On one side, there is side-on overlap between two p orbitals that are perpendicular to the plane of the ring on two adjacent C atoms. This is a relatively strong bonding pi-type bonding interaction. On the opposite side of the ring, the two carbon atoms form an identical pi-type interaction. This means that there is a nodal plane which runs through the plane of the molecule (running through the nodes centered on the 4 carbon atoms). There is also a second more significant nodal plane which runs through the centre of the ring, perpendicular to the plane of the molecule. This nodal plane represents a relatively strong pi-anti-bonding interaction: the lobes of electron density on opposite sides of the ring above and below the ring are of opposite phase. Hence, this is a weakly anti-bonding MO.
The Mo for borazine is very similar. Two pairs of p orbitals perpendicular to the plane of the ring on a N and B atom on opposite sides of the ring interact in a pi type interaction. This means there is a nodal plane running through the plane of the molecule (involving the nodes centred on the N and B atoms) and a nodal plane running through the centre of the ring which involved the lobes of electron density on either side of the ring interacting in a pi-type anti bonding interaction on either side of the plane of the ring. Hence this suggests this MO is also a weakly bonding pi-type MO. Since these MOs are strongly antibonding- they are higher in energy than the two MOs above. These MOs more strongly anti bonding than the two respective pairs of MOs above and hence are the highest in energy. |
Smf115 (talk) 17:57, 23 May 2018 (BST)Very thorough analysis of the MOs in terms of the AO contributions with the correct identification of sigma- and pi-type interactions and the MO character. To improve it would have been good to see a larger range in character seen across the MOs (label which MOs they are!) and consideration given to other factors such as electronegativity and symmetry when comparing the MOs across the molecules.
Investigation into the concept of aromaticity
A molecule is described as being aromatic if it obeys Huckel's Rule. This dictates that in order for a molecule to be aromatic it must have a planar structure, with a contiguous cyclic set of p orbitals perpendicular to the plane of the ring and a total of (4n+2) pi electrons (where n is an integer). [2] Furthermore, aromatic compounds are characterised by their unusual stability (they are more conjugated and hence more stable than the their olefinic analogues). They also possess "Ring-currents" due to the movement of delocalised pi electrons around the ring: these cause the Hs present outside the ring to be more deshielded (and hence have higher chemical shifts) while the Hs inside an aromatic ring are more shielded (and hence have lower chemical shifts). [2] [3] Due to their extensive delocalisation, the C-C bonds in aromatic compounds are typically shorter than C-C bonds but longer than C=C bonds, making them of intermediate strength. Finally, due to their favourable stability, aromatic compounds typically react to give aromatic products and undergo reactions such as nucleophilic/electrophilic aromatic substitution reactions. [3]
Typically, aromatic systems have been associated with benzene and planar pi-electron cyclic systems. Anti-aromaticity is the term used to describe planar, cyclic molecules with a contiguous set of p orbitals perpendicular to the plan of the ring with only 4n pi electrons. Anti-aromatic systems are exceptionally unstable and hence anti aromatic systems tend to pucker so as decrease the interaction between p orbitals and hence take up a more stable state. [2] More recently, groups of molecules that do possess all of the characteristics given above such as non-planar cyclic pi-electron systems, metallobenzenes and fullerenes have been suggested to posess aromatic behaviour. Quasi-aromaticity and pseudo-aromaticity are terms further used to describe possessing some aromatic features and molecules closely resembling aromatic systems respectively. [3]
Benzene has six p(z) orbitals (which are perpendicular to the plane of the ring) that interact in a p-p side interaction to form six different aromatic pi MOs. These involve a fully bonding MO which involves all the p orbitals interacting in phase, two degenerate weakly bonding MOs (a nodal plane running through the center of the molecule), two degenerate weakly anti-bonding MO with two nodal planes though the centre of the ring and a strongly anti-bonding MO in which all p orbitals are out-of-phase and there are 3 nodal planes running though the center of the ring. In benzene, only the bonding pi MOs are occupied since there are only 6 pi electrons giving it a "closed shell structure" and contributing to its stability. [2]
LCAO method for benzene: diagram taken from Chemistry stack exchange. [4]
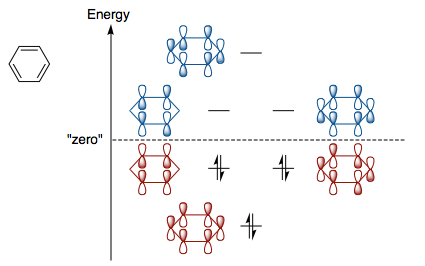
These three occupied pi bonding MOs are very similar to the computed MOs benzene and are shown below.
| Lowest energy pi MO | Weakly bonding pi MO | Weakly bonding pi MO | Weakly anti-bonding pi MO | Weakly anti-bonding pi MO | Strongly antibonding MO |
|---|---|---|---|---|---|
| ] |
|
 |
 |
 |
 ]
|
This suggest that the real occupied and unoccupied pi MO of benzene can be reasonably well predicted using the LCAO method. However, the real MOs are significantly more delocalised than those derived using the LCAO method. The computed MOs also suggest the bond length of the C-C bonds in benzene are made up of sigma and pi type interactions. Finally, the computed bonding occupied MOs are fully bonding and obey Huckel's rule and hence also suggest that benzene is aromatic.
While the pi-MO structure of benzene is often used to describe the unusual aromatic stability of benzene, it has been shown that the sigma molecular orbitals of benzene may itself have a significant effect on the structure and symmetry of the molecule and hence it is not sufficient to describe benzene using only the p(z) MO description. [3] [5]
Smf115 (talk) 18:03, 23 May 2018 (BST)Excellent and well referenced discussion of aromaticity. Great reference to the MOs visualised to explain why the overalpping pZ AO description is not adequate.
Smf115 (talk) 18:03, 23 May 2018 (BST)Overall a very good report!
References
- ↑ Dr. Hunt P. Lecture 4 Tutorial Problem Model Answers [Internet]. Molecular Orbitals in Inorganic Chemistry. 2018. Available from: http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year2a/Tut_MO_diagram_BH3.pdf.
- ↑ 2.0 2.1 2.2 2.3 Clayden J, Greeves N, Warren S. Organic Chemistry. 2nd ed. Oxford University Press; 2012. 276, 156-162 p.
- ↑ 3.0 3.1 3.2 3.3 Palusiak M, Krygowski TM. Application of AIM parameters at ring critical points for estimation of π-electron delocalization in six-membered aromatic and quasi-aromatic rings. Chem - A Eur J. 2007;13(28):7996–8006.
- ↑ Chemistry Stack Exchange[Internet]. What is the justification for Hückel's rule?. 2018. Available from: https://chemistry.stackexchange.com/questions/30927/what-is-the-justification-for-h%C3%BCckels-rule
- ↑ Kovačević B, Barić D,Maksić Z B, Müller T. The Origin of Aromaticity: Important Role of the Sigma Framework in Benzene. ChemPhysChem. 2004; 5: 1352–1364.