Rep:Mod:MAC01049979
NH3 molecule, N2 and H2 molecules
NH3 molecule
Important Information about optimized NH3 molecule
Molecule= NH3 , Ammonia molecule
Calculation method= RB3LYP
Basis set= 6-31G(d,p)
Final Energy, E(RB3LYP)= -56.55776873 au
RMS gradient= 0.00000485 au
Point group= C3V
Optimized N-H distance= 101.798 pm
Optimized H-N-H bond angle= 105.741o
The Item Table suggests that the structure is converged:
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986274D-10
Optimization completed.
-- Stationary point found.
Since at equilibrium there are no forces acting on the molecule, the slope of the energy vs. distance graph should be zero: i.e. at a minimum. The value of the forces (and displacement) are very close to zero suggesting and a minimum has been found. Therefore the system is at equilibrium and the structure represented above is has the lowest energy geometry.
Optimized ammonia molecule |
The optimisation file is liked to here
Information about the vibrations of the optimized NH3 molecule
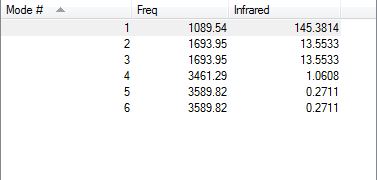
The information about the vibrations of the optimized molecule are show below.
All the frequencies given are positive suggesting that the structure is fully optimized.
From the 3N-6 rule we can expect 6 vibrational modes.
Vibrational modes of 5 and 6 have the same energy (are degenerate). Vibrational modes of 2 and 3 are also degenerate.
The vibrational modes of 1, 2 and 3 are bending vibrations. The vibrational modes of 4, 5, 6 are bond stretch vibrations. Vibrational mode 4 is highly symmetric. Vibrational mode 1 is an umbrella mode.
Vibrational mode 4 is involves a symmetrical stretching of the N-H bonds - this will not cause a change in dipole moment and hence will not be visible on the IR spectrum. Vibrational modes 5 and 6 have a very low intensity of 0.2711, suggesting that they will not be visible on the IR spectrum. Vibrational modes 2 and 3 are degenerate (have the same frequency) and will appear at the same frequency on the spectrum. Hence, overall one would expect to see only 2 bands on the IR spectrum for gaseous ammonia at a frequency of 1089.54 cm-1 and 1693.95 cm-1.
Charge analysis of the NH3 molecule
It is expected that the N atom will be negatively charged because N is more electronegative than H. It is expected that H will be positively charged because the H atom is less electronegative (electronegativity of H=2.20) than the N atom (electronegativity of N=3.04). The charge given by the NBO analysis is given as 0.375 for each of the H-atoms and -1.125 for the N-atom hence confirming the prediction made above.
N2 molecule
Important Information about optimized N2 molecule
Molecule= N2 , Nitrogen molecule
Calculation method= RB3LYP
Basis set= 6-31G(d,p)
Final Energy, E(RB3LYP)= -109.52412868 au
RMS gradient= 0.00000060 au
Point group= Dinfh
Optimized N-N distance= 110.550 pm
The Item Table suggests the structure is converged:
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.400994D-13
Optimization completed.
-- Stationary point found.
A stationary point has been found suggesting the system is at equilibrium and that the structure is optimized.
Optimized molecule |
The optimisation file is liked to here
Information about the vibrations of the optimized N2 molecule
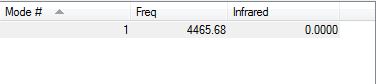
The information about the vibrations of the N2 optimized molecule is show below.
There are no negative frequencies suggesting that the optimization is complete. The frequency shown at 2457.33 cm-1, which consists of a symmetric stretch, will not cause a change in dipole moment and therefore N2 can be considered IR inactive.
Charge analysis of the molecule was done and both N atoms were found to have no charge (0.000) as would be expected for the neutral molecule.
H2 molecule
Important Information about optimized H2 molecule
Molecule= H2 , Hydrogen molecule
Calculation method= RB3LYP
Basis set= 6-31G(d,p)
Final Energy, E(RB3LYP)= -1.17853936 au
RMS gradient= 0.00000017 au
Point group= Dinfh
Optimized H-H distance= 74.279 pm
The Item Table suggests that the structure is converged since a stationary point has been found:
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
A stationary point has been found suggesting the system is at equilibrium and that the structure is optimized.
Optimized molecule |
The optimisation file is liked to here
Information about the vibrations of the optimized H2 molecule
The information about the vibrations of the optimized H2 molecule is show below.
There are no negative frequencies suggesting that the optimization is complete.
As expected, both H atoms have neutral charge (0.000).
The Haber Bosch process
Although discovered more than one hundred years ago, the Haber Bosch process remains the one of the key ways in which NH3 is produced on an industrial scale today.[1] The process consists of reacting Nitrogen and Hydrogen gas together under high temperature and pressure (500oC and 20 MPa).[1] The ammonia produced via the Haber-Bosch cycle was used to produce the N-base fertilizers essential for food crop growth, and allowed the food production levels to sustain the massive increase in the global population throughout the 20th century. [2] The industrial process is used to meet approximately 66% of the global NH3 demand and it is estimated that the process sustains approximately 40% of the global population.[1][2]
Energy of reaction between hydrogen and nitrogen (Haber-Bosch process)
The reaction considered is the following: N2 + 3H2 --> 2NH3
The calculations used to determine the energy for the reaction.
E(NH3)= -56.55776873 au
2*E(NH3)= -113.11553746 au
E(N2)= -109.52412868 au
E(H2)= -1.17853936 au
3*E(H2)= -3.53561808 au
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]
ΔE= -113.11553746-[-109.52412868+(-3.53561808)]
ΔE= -0.05579070 au
ΔE= -146.48 kJ/mol
Hence, 146.48 kJ/mol is released for the conversion of hydrogen and nitrogen gas into ammonia. The value of the change in energy for the reaction is negative: ΔE= -146.48 kJ/mol. This suggests that the product, NH3 is more stable than the gaseous hydrogen and nitrogen reactants.
Molecule of choice: ClF3
The molecule chosen for analysis was ClF3. The molecule was determined to have a 'T-shape' since the central Cl atom has 2 sets of lone pairs in the equatorial position and has 3 Cl-F single bonds. This molecule was determined to have a point group of C2V.[3]
Information obtained from the optimization of the ClF3 molecule
Molecule= ClF3, Chlorine Trifluoride
Calculation method= RB3LYP
Basis set= 6-31G(d,p)
Final Energy, E(RB3LYP)= -759.46531688 au
RMS gradient= 0.00002465 au
Point group= C2V
Optimized Cl-Fax distance= 172.863 pm
Optimized Cl-Feq distance= 165.143 pm
Optimized Fax-Cl-Fax bond angle= 87.140o
Optimized Feq-Cl-Feq bond angle= 174.281o
Item Value Threshold Converged?
Maximum Force 0.000050 0.000450 YES
RMS Force 0.000028 0.000300 YES
Maximum Displacement 0.000204 0.001800 YES
RMS Displacement 0.000134 0.001200 YES
Predicted change in Energy=-1.250222D-08
Optimization completed.
-- Stationary point found.
A stationary point has been found suggesting that the optimization is complete and that the system is at equilibrium.
Optimized molecule |
The optimisation file is liked to here
Information obtained from the vibrations of the optimized ClF3 molecule
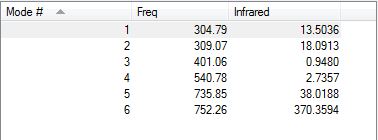
All the frequencies obtained as shown below are positive values suggesting that the molecule is fully optimized.
The information about the vibration analysis of the ClF3 molecule are shown below. All frequencies are positive suggesting that the structure is optimized.
Using the 3N-6 rule, 3(4)-6=6 , six different vibrational modes are expected for the molecule. According to the image above there, are 6 different vibrational modes as expected. None of the vibrational modes are symmetrical and so all the vibrational modes can be expected to produce a change in dipole moment. The asymmetric stretch at a frequency of 752.26 cm-1 is the vibrational mode with the greatest amplitude (370.3594 cm-1) and consists of an asymmetric stretch. Vibrational modes 3 and 4 both have exceptionally weak intensities of 0.9480 and 2.7357 respectively and hence they are not expected that the will appear on the IR spectrum of the molecule. Hence, it is expected that the ClF3 will have 4 visible bands on its IR spectrum.
Information obtained from the charge analysis of the optimized ClF3 molecule
Fluorine atoms are more electronegative than Cl atoms since these have electronegativities of 4.0 and 3.0 respectfully. Hence, it can be expected that the Cl will be positively charged while the F atoms will be negatively charged.
The charge analysis was used to determine the charges on each atom in the molecule: the central Cl atom was found to have a charge of 1.225, the equatorial F atom was found to have a charge of -0.315, while the two axial F atoms were found to have a charge of -0.454. Hence, this lies in parallel with the predicted charges above.
Analysis of 5 molecular orbitals from the optimized ClF3 molecule
The molecular orbitals below give some information about the types of bonding and which atomic orbitals contribute to bonding interactions within the molecule.
Molecular Orbital 1
This is an occupied bonding molecular orbital between the central chlorine atom and the 3 fluorine atoms. There are no nodes anywhere within the molecular orbital: this suggests that it is made from an s orbital from the chlorine atom and an s orbital from each of the F atoms all interacting in-phase. It is the lowest energy bonding molecular orbital, since only non-bonding orbitals are lower in energy, and it can therefore be considered to be deep in energy. Since the molecular orbital consists of a filled bonding molecular orbital between the central Cl-atom and the 3 F-atoms, this molecular orbital will contribute to the formation of a sigma bond between the Chlorine-atom and each of the three Fluorine-atoms. Hence, the molecular orbital can be considered an occupied sigma-type molecular orbital.
Molecular Orbital 2
The molecular orbital consists of an occupied anti-bonding orbital: it consists of the s orbital on the central Cl-atom and the s orbitals of each of the three F atoms meeting out-of-phase. It is the anti-bonding equivalent of 'Molecular Orbital 1' (shown above) since it consists of out-of-phase interactions between an s orbital from each of the atoms in the molecule. Therefore, it can be considered a sigma-star type anti-bonding molecular orbital. Because of its anti-bonding character, this molecular orbital is higher in energy than 'Molecular Orbital 1' and contributes to decreasing the sigma-bond character between the Cl-atom and each of the three F-atoms.
Molecular Orbital 3
'Molecular Orbital 3' consists of a bonding interaction between a p orbital on the central chlorine atom and an s orbital from each of the two axial fluorine atoms. The presence of a node on the central Chlorine atom suggests that this molecular orbital involves a p-orbital from chlorine. The molecular orbital is deeper in energy than 'Molecular orbital 2' since it consists of a bonding sigma-type interaction between the Cl-atom and the two axial F-atoms. Therefore, the molecular orbital can be considered a sigma-type molecular orbital which contributes to the formation of a sigma bond between the chlorine atom and each of the two axial fluorine atoms.
Molecular Orbital 4
'Molecular orbital 4' consists of a filled molecular orbital with a mixture of bonding and anti-bonding character. Because of its anti bonding-character, this molecular orbital is higher in energy than the 'Molecular Orbitals 1, 2 and 3'.
There is a bonding interaction between the chlorine atom and the axial fluorine atoms. The presence of a nodal plane running parallel to the Fax -Cl- Fax bond suggest that this bonding interaction is produced by p orbitals from the Cl and Fax atoms meeting in-phase in a pi-like fashion. The presence of electron density of opposite phase above and below the nodal plane running parallel to the Fax -Cl- Fax atoms suggests that this is a pi-type interaction contributing to strengthening each of the Fax -Cl bonds i.e. increasing the pi-character of the Fax -Cl bonds.
There is a anti-bonding interaction between a p orbital on the equatorial fluorine atom (recognized by the presence of a nodal plane on the equatorial fluorine atom) and the bonding-system between the Fax -Cl- Fax atoms. The present of electron density of opposite phase above and below the plane of the molecule suggest that this is potentially a pi-star type interaction. Since the molecular orbital is filled, this suggests that this anti-bonding interaction weakens the Cl-Feq bond.
Molecular Orbital 5
'Molecular Orbital 5' is the highest energy occupied molecular orbital i.e. the HOMO. The molecular orbital has a nodal plane which runs parallel to the plane in which the molecule lies and has nodal planes that run perpendicular to this plane, through the center of each of the Cl-F bonds. This suggests that this molecular orbital is an anti-bonding molecular orbital, made up of p orbitals form each of the atoms in the molecule meeting out of phase. Therefore, this molecular orbital consists of a pi-star type molecular orbital that contributes to decreasing the strength (and increasing the length) of each of the Cl-F bonds.
Further investigation of the bond lengths and vibrations of H2SiO
The bond lengths, vibrations and shape of the molecular orbitals of a H2SiO molecule was investigated using Gaussview.
A comparison of the bond lengths obtained for H2SiO using GaussView with a literature value
GaussView was used to find the optimum structure for a H2SiO molecule. The parameters set for the optimization and the results obtained are shown below.
Molecule= H2SiO
Calculation method= RB3LYP
Basis set= 6-31G(d,p)
Final Energy, E(RB3LYP)= -365.90001403 au
RMS gradient= 0.00000941 au
Point group= C2V
Optimized Si=O distance= 153.172 pm
Optimized Si-H distance= 148.652 pm
The log file indicates that a stationary point has been found - this suggests that the forces have converged and that the structure is fully optimized. The optimisation file is liked to here
Item Value Threshold Converged?
Maximum Force 0.000023 0.000450 YES
RMS Force 0.000009 0.000300 YES
Maximum Displacement 0.000022 0.001800 YES
RMS Displacement 0.000015 0.001200 YES
Predicted change in Energy=-4.981734D-10
Optimization completed.
-- Stationary point found.
Optimized molecule |
The optimized bond Si=O and Si-H bond lengths for the molecule were found to be 153.2 pm and 148.7 pm. The value of the Si=O and the Si-H bond lengths are given in literature as 150.5 pm and 149.1 pm respectively.[4] Therefore, the bond length values obtained from the optimized structure in GaussView are reasonably similar to values obtained from literature. This could potentially suggest that the bong lengths obtained for this molecule using GaussView are reasonably accurate.
Vibrational analysis of H2SiO and comparison to values obtained from literature
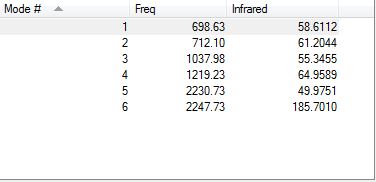
The information about the vibration analysis of the H2SiO molecule is shown below.
The frequencies of the vibrational modes are all positive suggesting that the structure of the molecule has been fully optimised. As expected from the 3N-6 rule (3(4)-6=6), 6 modes are vibration can be seen. All 6 of the vibrational modes at 698, 712, 1037, 1219, 2230 and 2247 cm-1 have relatively high intensities suggesting that all 6 vibrational modes will be visible on the IR spectrum of H2SiO. The vibrational mode with the highest intensity at a frequency of 2247 cm-1 is caused by an asymmetric H-Si stretch. Furthermore, the modes at 1219 and 2230 cm-1 are caused by stretching of the Si=O bond and symmetric H-Si stretching receptively. [4]
For H2SiO, 6 vibrational modes are given in literature at frequencies of 706, 712, 1023, 1217, 2223 and 2238 cm-1.[5] These values are reasonably similar to the values obtained using the optimized structure in GaussView. This suggests that the values obtained in GaussView are reasonably accurate.
References
- ↑ 1.0 1.1 1.2 R. D. Milton, R. Cai, S. Abdellaoui, D. Leech, A. L. De Lacey, M. Pita and S. D. Minteer, Angew. Chemie Int. Ed., 2017, 56, 2680–2683.
- ↑ 2.0 2.1 N. Cherkasov, A. O. Ibhadon and P. Fitzpatrick, Chem. Eng. Process. Process Intensif., 2015, 90, 24–33.
- ↑ P. Schwerdtfeger, J. Phys. Chem. A, 1996, 100, 2968–2973
- ↑ 4.0 4.1 G. Canevari, G. Onida and K. Gaal-Nagy, J. Phys. Condens. Matter, 2008, 20.
- ↑ M. Hargittai, J. Phys. Chem. A, 2004, 108, 10194–10199.