Rep:Mod:Logopolis
Abstract
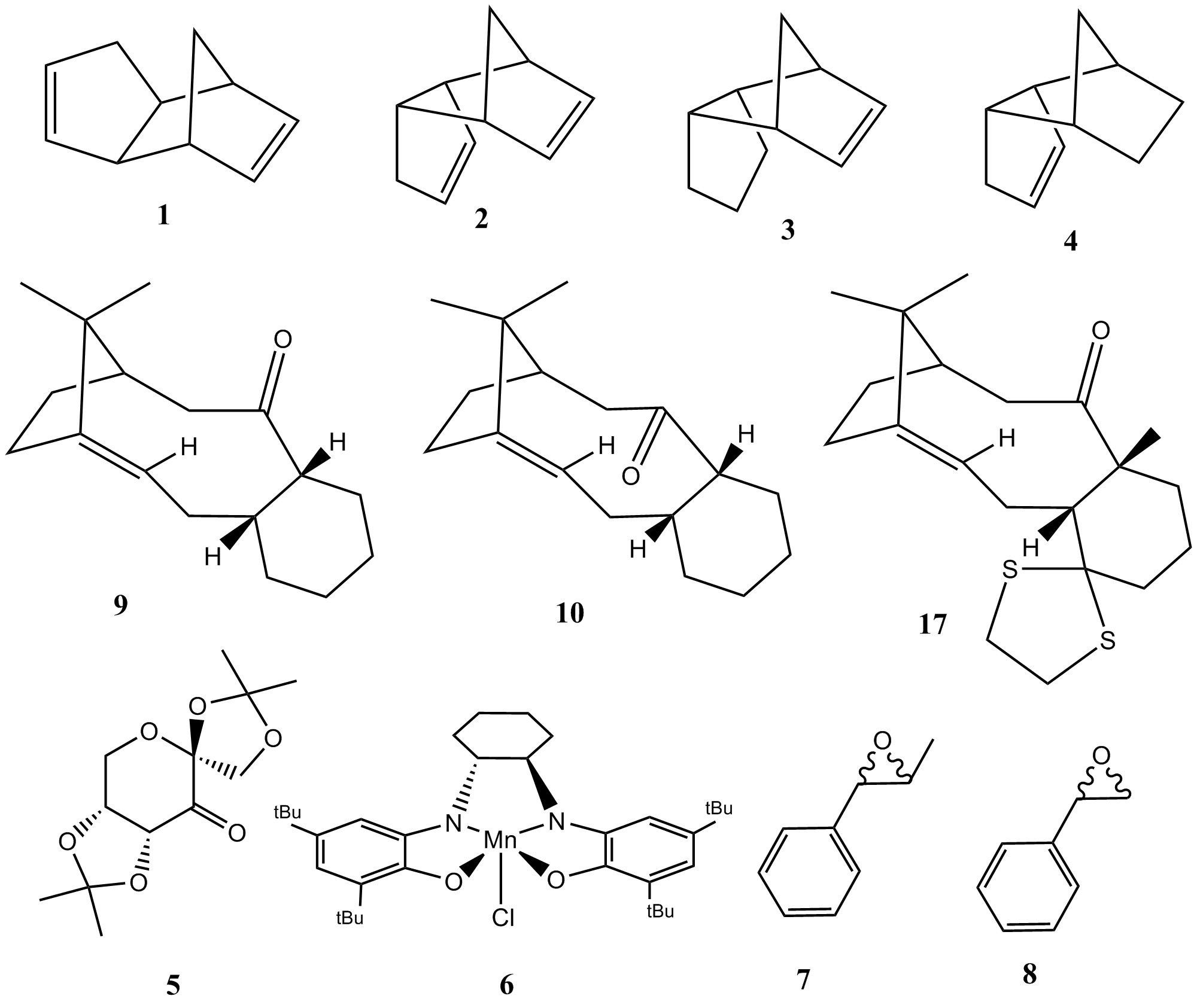
Calculations of increasing complexity have been conducted on a series of bicyclic molecules 1-4, 9, 10 and 17, culminating in a high level prediction of the NMR properties of 17 with the intention of evaluating an assigned conformation. Later investigations focused on using less familiar computational techniques to probe asymmetric epoxidation catalysts 5-6 and the stereochemical identity of two previously synthesised epoxides 7 and 8.
Investigations using Molecular Mechanics
Dicyclopentadiene
The dimerisation of cyclopentadiene proceeds by a [4+2] pericyclic reaction and is a prototypical example of the 'endo transition state rule' ie. the product most readily formed is the one in which the bulk of the dienophile ends up on the same face as the bulk of the diene. Given that dicyclopentadiene may be considered a substituted bicyclo[2.2.1] system, this would place the second ring in the endo position, hence the nomenclature.
The hydrogenation of said compound is of considerable commercial interest due to its use in the synthesis of adamantane, first reported in 1957[1], and now carried out on industrial scales. (it is also somewhat of a benchmark for the investigation of new hydrogenation catalysts[2][3]) Isomerisation of the fully hydrogenated tetrahydro-dicyclopentadiene to the exo form has also shown significant promise in the field of high energy density fuels (as the endo isomer has much less desirable properties[4]). As such, the theoretical aspects relating to the stability of these compounds is not without practical application, while the simplicity of their elemental makeup allows for an accurate assessment of their mechanical parameters without needing to resort to quantum mechanics.
To this end, a molecular mechanics simulation has been conducted on:
- The two possible dimerisation products, and
- The two possible dihydro derivatives of the endo-dimer
using the MMFF94s force field, the results of which are presented below.
| Molecule | Electrostatic Energy Contribution | Value/kcalmol-1 | Molecule | Electrostatic Energy Contribution | Value/kcalmol-1 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
Bond Stretching
Angle Bending Stretch Bending Torsion Out of Plane Bending Van der Waals Electrostatic TOTAL |
3.54313
30.77265 -2.04139 -2.73060 0.01486 12.80113 13.01370 55.37344 |
|
Bond Stretching
Angle Bending Stretch Bending Torsion Out of Plane Bending Van der Waals Electrostatic TOTAL |
3.46746
33.19152 -2.08213 -2.94935 0.02197 12.35710 14.18415 58.19070 | ||||||
|
Bond Stretching
Angle Bending Stretch Bending Torsion Out of Plane Bending Van der Waals Electrostatic TOTAL |
3.30800
30.86182 -1.92647 0.06454 0.01534 13.27880 5.12098 50.72283 |
|
Bond Stretching
Angle Bending Stretch Bending Torsion Out of Plane Bending Van der Waals Electrostatic TOTAL |
2.82311
24.68537 -1.65718 -0.37835 0.00028 10.63724 5.14702 41.25749 |
The initial conclusion afforded by this treatment is that the endo form is a higher energy configuration than the exo, and therefore its' formation must be a kinetically controlled process with a more stable transition state. This may be a relatively non controversial statement however the reasons for this (and endo selectivity in general) have been the subject of debate for some time.

The accepted explaination for the stabilisation of the endo transition state is a favourable secondary orbital overlap[5] of the occupied (yet not frontier) π orbitals in the 4nπ system and the 2nπ system. However this fails to explain the preference for endo in the pre-hydrogenated (ie cyclopentadiene with cyclopentene) pericyclic reaction[6], which results in the formation of compound 3, an in which there are no secondary orbital overlaps possible. This was rationalised at the time by invoking a steric interaction in the exo transition state associated with the approach of the (in this case) blue methylene group and black ring, that destabilises in both the saturated and unsaturated reaction mechanisms. This effect has been verified subsequently[7].
Hydrogenation product 4 has shown itself to be mechanically more stable than its norbornene-like isomer 3, and this manifests itself in all components excluding electrostatic (indeed, the torsional energy is actually destabilising in the latter case). 3 also possesses the largest VdW energy of any of four molecules. This can be understood in that, among other things, it incurs two large 1,2-diaxial interaction between the methylene and methyne hydrogens in the bottom ring (in 4 the hydrogens are added laterally away from the ring bridging methynes). There is also a large discrepancy in the angle bending energies of the two molecules, likely a manifestation of the conformations of the fully hydrogenated cyclopentane rings. In 3 it is quite considerably distorted from the lowest energy half chair conformation - dihedral angles are all between 20 and 35° - whereas in 4 they are all close to 60° (an example of this is shown visually in the JMol figures). The reported difficulty associated with the second hydrogenation may be an example of hyperstability of the alkenes (covered in the next section) but any conclusions achieved presently are done so in the absence of any information regarding the reaction mechanism - solid state Lindlar catalysis may severely disfavour the formation of 3 for example, due to the shape of the molecule precluding it from approaching at the right trajectory.
References
- ↑ P.R. Schleyer, J. Am. Chem. Soc., 1957, 79, 3292
- ↑ M. Navrátilová, K. Sporka, Applied Catalysis A., 2000, 203(1), 127
- ↑ L. Wu, M. Ji, M. He, T. Cai, Chinese Journal of Catalysis, 2007, 28(7), 585
- ↑ H.S. Chung, C.S.H. Chen, R.A. Kremer, and J.R. Boulton, Energy and Fuels, 1999, 13, 641
- ↑ R. Hoffmann, R.B. Woodward, J. Am. Chem. Soc., 1965, 87, 4388
- ↑ M. A. Fox, R. Cardona, N.J. Kiwiet, J. Org. Chem., 1987, 52 (8), 1469
- ↑ I. Fernández, F.M. Bickelhaupt, J. Comp. Chem., 2014. 35(5), 371
Taxol Intermediates
The second compound investigated in this work provides examples of two subtle mechanical effects that both alter its organic reactivity, and both of which involve unusually large energetic benefits accrued: the first, of one conformational minimum over another; and the second, of an unsaturated system over a saturated one. In the context of a synthetic intermediate these effects are detrimental as they introduce uncertainty into both the identity of your compound and the feasibility of concluding the synthesis, but from a computational standpoint they can be eaily identified. Previous molecular mechanics studies on bicyclic [6.2.1] compounds[1] have involved the use of rotamer searching to establish low energy conformations, whereas unsaturated variants of this ring structure[2] only appear to have been probed using the less advanced MMX force field, if at all. While the utilised modelling program (Avogadro) contains a rotamer searching facility, (courtesy of OpenBabel[3]), the defined stereochemistry about the ring junctions and double bond, as well as the presence of an extra ring, indicate that this would not be a worthwhile procedure. Indeed, the only rotation that appears to be 'searchable' in the sense that multiple minima can be achieved is that of the carbonyl, which is the very effect under discussion here.
Atropisomerism
A variety of conformations of the structures 9 and 10 have been investigated using the MMFF94s force field. Several orientations in which the cyclohexane adopts a chair in 9 were found, the most stable of which involves the back methylene facing away from the carbonyl (shown below). This gave rise to nice gauche interactions about the bond linking the 6 and 10 membered rings, with two antiperiplanar σC-H > σ*C-C relationships observable (and an arguably favourable[4] σC-C > σ*C-O overlap). It is speculated that there also exists an intramolecular hydrogen bond between the carbonyl and the protons on the methyl situated at the apex of the bridge, the distance between them being only 2.28Å (although these are both of course beyond the level of theory inherent in this calculation).
The motif in which the 'back' of the chair is geometrically opposite to the carbon-oxygen bond of the carbonyl is repeated in the lowest energy state of rotamer 10, which optimises to a slightly lower total energy. Given that the reported[5] isomerisation takes place under equilibrating conditions (albeit with a barrier low enough that it takes place at room temperature) it is concluded that alkene 10 is the favoured atropisomer.
A search of the Cambridge Crystal Structure Database has been conducted using the structural formula of the considered alkene to discern whether recorded conformations in the solid state duplicate that found by this treatment. No exact crystal structure of this compound appears to have been published, however a small sample[6][7] of (cyclohexane-)ring substituted compounds have been found, and each corresponds almost exactly to the optimised structure of 10. A rotatable version of an acyl-substituted alkene is provided directly from the published coordinates. . The features of note are the carbonyl position, which replicates very well; the angle about the cyclohexane ring junction subtended by the methylene group α to the olefin (113.8 vs. 116.8°); and the dihedral angle about the double bond (12.8 vs. 12.5°). Given the drawbacks of X-ray crystallography, it should be noted that hydrogen atoms are included merely for completeness and may not reflect their actual positions in the crystal structure.
Hyperstability
Bicyclic/Polycyclic alkenes where the olefins are placed at the bridgehead frequently encounter endothermic heats of hydrogenation[8]. This effect becomes more pronounced around middling ring size[9] and constitutes an exceptional thermodynamic system, known as hyperstability.
The term 'olefinic strain' is defined by Maier & Schleyer as the total strain of the hydrogenated product minus the strain of the alkene, and is expected to be negative in at least the lower energy product. This was expectedly found to be the case for both 9 and 10 (OS= -7.337kcal/mol for 9, -8.99384 for 10), but would decrease by a small amount in a hypothetical hygrogenation of 9 simultaneous with 'atropisomerisation'. Values are smaller than those for similar ring sizes and saturation levels (-14.2kcal for 6.2.2)9, but still allow us a full explanation of the known unresponsiveness to hydrogenation. The contention that 'Since OS values are obtained by subtraction, errors inherent in the calculations should tend to cancel'8 appears to be a quite naive assumption; there doesn't seem to be any correlation between functional groups present and the tendency of the calculation to over/underestimate. It is only because of the large energy differences reached that it is deemed useful to compare the strain properties of two molecules of differing empirical formulae in this way. An alternative may have been to shift the double bond anticlockwise one increment around the ring, but the established publication history in this area indicated an OS would be more useful in quantifying hyperstability.
- ↑ B. Mi, R.E. Maleczka, Tetrahedron Lett., 1999, 40, 2053
- ↑ M.G. Constantino, K.T. de Oliviera, A. Beatriz, G.V.J. da Silva, Magn. Reson. Chem., 2003, 41, 726
- ↑ O’Boyle et. al, J. Cheminformatics, 2011, 3, 33
- ↑ I.V. Alabugin, T.A. Zeidan, J. Am. Chem. Soc., 2002, 124, 3175
- ↑ Paquette, L.A., Combrink, K.D., Elmore, S.W., Rogers, R.D., J. Am. Chem. Soc, 1991, 113, 1335
- ↑ L.A.Paquette, S.K.Huber, R.C.Thompson, J. Org. Chem., 1993, 58, 4952
- ↑ L.A.Paquette, R.C.Thompson, J. Org. Chem., 1993, 58, 6874
- ↑ W.F. Maier, P.V.R. Schleyer, J. Am. Chem. Soc., 1981, 103, 1891
- ↑ A.B. McEwan, P.V.R. Schleyer, J. Am. Chem. Soc., 1986, 108, 3951
Investigations using Quantum Mechanics
Taxol Intermediates
NMR Prediction
The proximity of a heavy atom imposes strong consequences on the magnetic environments of elements and can significantly alter an NMR spectrum (this is used to the chemists advantage in the field of Lanthanide shift reagents[1]). The molecule under discussion, 17, contains two sulphur atoms and has understandably been found extremely sensitive to changes in it's spatial orientation.
Initial prediction of the 1H spectrum to the B3LYP/6-31G(d,p) level[2] was done with an input that broadly satisfied the coordinates reached for molecule 9 with molecular mechanics earlier, and correlated with that assigned in the leading reference[3]. The output spectrum was found to discriminate too drastically between protons within each of the methyl environments, as rotation is not considered within the calculation. This was corrected as instructed (assuming a uniform field gradient, the mean of the three shifts may be taken) and the spectrum became significantly closer to that recorded. Analysis of the extent of this is difficult as not all environments were resolved in the original work, meaning relative errors are only calculable for a portion. Nonetheless, at this point, some significant anomalous features remained. The alkene proton was predicted to be almost 0.4ppm downfield of it's observed value (7.5% relative error) and this deviation remained for all subsequent calculations done. This is not believed to be due to an inaccurate geometry optimisation as it's position is entirely defined by the oxy-cope process used to form 17. It is also consistent with the established literature[4] for bridgehead [6.2.2] systems and the tendency for the alkene proton to project out[5] of the bicyclic cage.
The prediction for the methyne environment α to the dithiolane unit (atom 19) places it degenerate with several of the dithiolane (S-CH2) protons. These were themselves slightly downfield of their recorded shifts in both the 17 spectrum and that of 1,3-dithiolane in CDCl3[6]. Perhaps unsurprisingly, the 13C spectrum also produced anomalously high shifts for atoms in close proximity to sulphur.
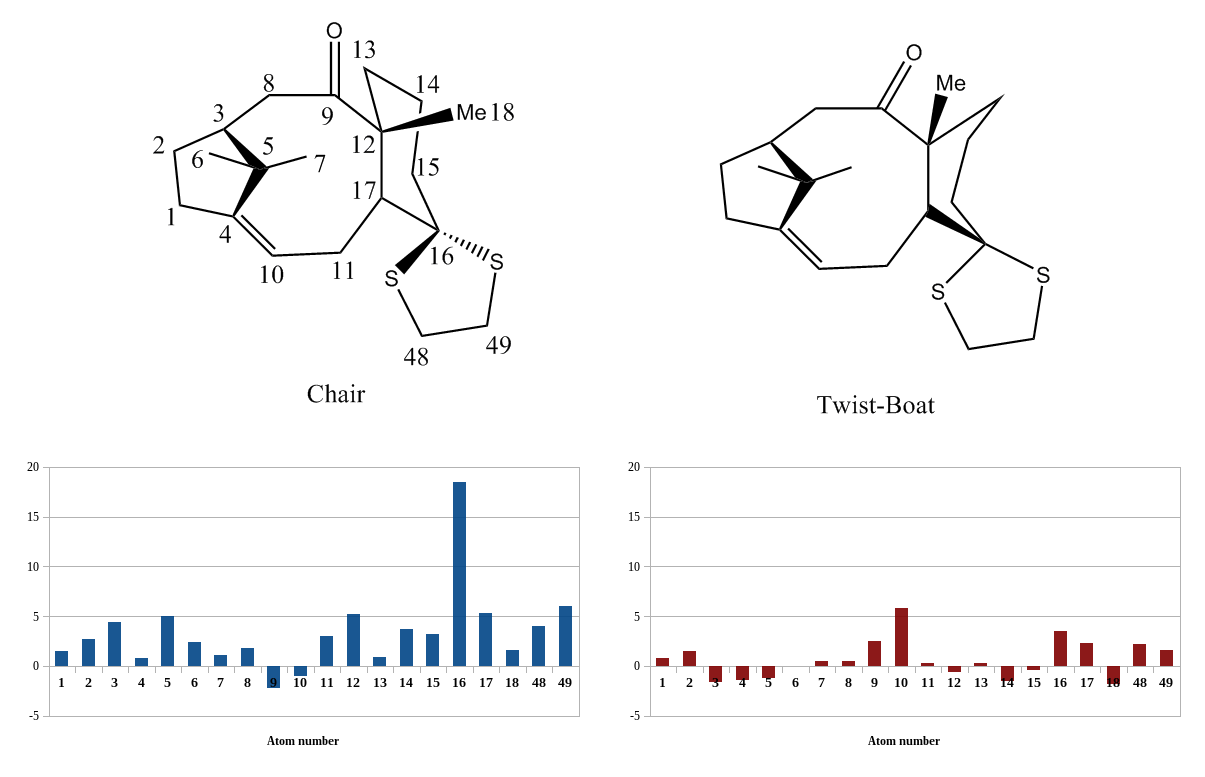
To try and alleviate some of these inconsistencies a conformational tweak in the vicinity of the spirocyclic carbon was attempted and a second B3LYP/6-31G(d,p) NMR prediction[7] was done using the most stable twist-boat conformer achievable. This significantly improved the 13C spectrum, with a Mean Absolute Error[8] of 0.663ppm, compared to 3.401ppm for that of the chair, but sharply increased the errors in many of the 1H environments (a more detailed overview of this can be seen in figures 3 and 4). It was also found to have a less negative free energy than the chair conformation - disfavouring its formation. The most distinctive feature of the data is that the proton deviations possess identical directionality and relative magnitude in both predictions, merely differing in absolute magnitude. It is unknown if the error is truly asymmetric about zero as so many of the proton environments do not have an associated literature value. Operating under the assumption that there is, one explanation is a bias in the referencing model[9].
This may be statistically quantified by performing a linear regression of calculated shielding values with observed shifts[10], and using the intercept as a reference. This treatment was done with all possible proton values (6 data points each) in both predicted spectra and was successful in both the case of the chair (0.1% relative error from literature intercept) and, to a lesser extent, the twist boat (6.5% relative error). This might appear to undermine the validity of the twist boat conformation but it should be noted that the calculations in the quoted study pertained to gas phase NMR, and so do not account for differing solvent/solute interactions (or rather, the simulation of them at this theory level). This course of investigation was ceased as no information could be found regarding the internal reference used (TMS vs. CDCl3) for 17 in the synthetic work, and this was discerned to be the most likely cause of any bias in δ found.
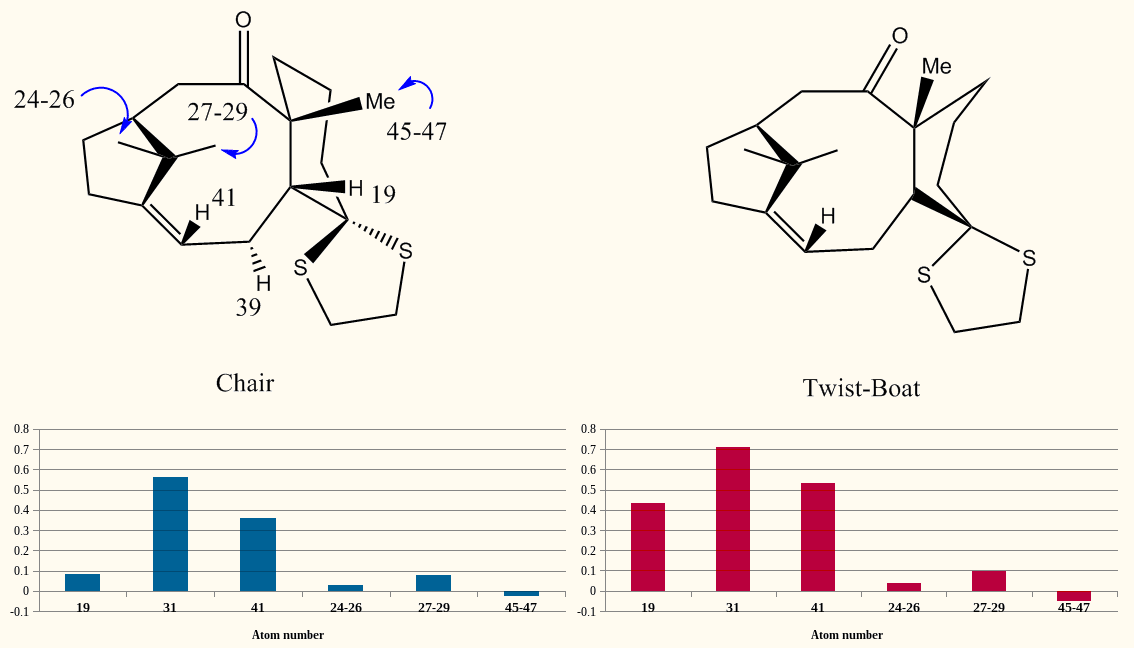
The two computed spectra place protons 39 and 19 in the opposite order to each other, and there was an initial uncertainty regarding the identity of the 2.99ppm environment. The similar magnitude of the two coupling constants reported implies two 3JHH couplings, rather than one 3JHH and one geminal 2JHH coupling (as would be the case for 39). Computational verification of this would be prohibitively long, and so qualitatively it may be taken that atom 19 is this environment.The consistent deshielding of the olefinic proton in all reported calculations is somewhat unfortunate although there is some basis for this in the simulation of bicyclic molecules (if only for [2.2.1] systems)[11].
Conclusions
Two possible geometries of the molecule 17 have been simulated to assess literature NMR assignment. Significant steps were made in the reproducability of the 13C NMR by introducing a twist-boat motif, but this was at the expense of both 1H and free energy considerations. On balance, the literature assignment is the closest to fulfilling all recorded data of any investigated conformation, but the aforementioned superior fit of the twist boat carbon resonances still leaves the possibly open for a wrong assignment. Flux is not believed to contribute significantly to the published NMR spectra.
- ↑ R.E. Sievens, in Nuclear Magnetic Resonance Shift Reagents, Elsevier, 1973
- ↑ S. Ingram, 2014, DOI:10042/27430
- ↑ L. Paquette, N.A. Pegg, D. Toops, G.D. Maynard, R.D. Rogers, J. Am. Chem. Soc., 1990, 112, 277
- ↑ Y. Tobe,Y. Ueda,M. Matsumoto,Y. Sakai,Y. Odaira, Tetrahedron Lett., 1982, 23, 537
- ↑ A.B McEwan, P.R. Schleyer, J. Am. Chem. Soc., 1986, 108, 3951
- ↑ Y.J. Cao, Y.Y. Lai, H. Cao, X.N. Xing, X. Wang, W.J. Xia, Canadian Journal of Chemistry, 2006, 84(11), 1529
- ↑ S. Ingram, 2014, DOI:10042/27429
- ↑ S. G. Smith, J. M. Goodman, J. Org. Chem., 2009, 74(12), 4597
- ↑ R. Jain, T. Bally, P.R. Rablen, J. Org. Chem., 2009, 74(11), 4017
- ↑ P.R. Rablen,S.A. Pearlman, J. Finkbiner, J. Phys. Chem. A, 1999, 103, 7357
- ↑ R.J. Abraham, M. Canton, L. Griffiths, Magn. Reson. Chem., 2001, 39, 421
Supplementary Information
Chair Carbon:
# SCF GIAO Magnetic shielding # X-Axis: Shift (ppm) # Y-Axis: Degeneracy # Reference: TMS B3LYP/6-31G(d,p) Chloroform # Reference shielding: 192.17 ppm # NMR Degeneracy Tolerance: 0.05 # # X Y Degeneracy 9-C 216.5978105634 1.0000000000 1.0000000000 4-C 145.4190065757 1.0000000000 1.0000000000 10-C 124.3189635428 1.0000000000 1.0000000000 16-C 91.4020527521 1.0000000000 1.0000000000 17-C 61.4600990483 1.0000000000 1.0000000000 12-C 57.7469779867 1.0000000000 1.0000000000 3-C 52.8846669677 1.0000000000 1.0000000000 5-C 51.7983544341 1.0000000000 1.0000000000 8-C 47.5325072161 1.0000000000 1.0000000000 48-C 43.8458973410 1.0000000000 1.0000000000 15-C 41.9960842893 1.0000000000 1.0000000000 49-C 41.8778382377 1.0000000000 1.0000000000 11-C 35.6298712513 1.0000000000 1.0000000000 2-C 31.5320137722 1.0000000000 1.0000000000 13-C 29.1980880461 1.0000000000 1.0000000000 18-C 28.5040297787 1.0000000000 1.0000000000 1-C 27.1114481177 1.0000000000 1.0000000000 6-C 26.3106226605 1.0000000000 1.0000000000 14-C 24.6714197788 1.0000000000 1.0000000000 7-C 19.8492446603 1.0000000000 1.0000000000

Chair Proton
# Summary of NMR spectra (SCF GIAO Magnetic shielding)
# Values for element H only
# Reference: TMS B3LYP/6-31G(d,p) Chloroform
# Reference shielding: 31.7462 ppm
# Degenerate peaks are condensed together (Degeneracy Tolerance 0.05)
#
# Shift (ppm) Degeneracy Atoms
5.2013609364 1.0000 41
3.1865151402 1.0000 51
3.0752627043 4.0000 50,52,19,53
2.7829444998 2.0000 40,39
2.7058232264 1.0000 20
2.5788079193 1.0000 28
2.4483961344 1.0000 44
2.3667551878 1.0000 43
2.2804644573 3.0000 23,21,34
2.1268047820 2.0000 30,38
2.0361564399 2.0000 46,33
1.8570278135 1.0000 35
1.5908477196 3.0000 26,22,32
1.4603828135 1.0000 31
1.0499133892 1.0000 47
0.8990108205 4.0000 24,27,25,29
0.5832657922 1.0000 45
Post Averaging:
1.4589 3.0000 27,28,29
1.2231 3.0000 45,46,47
1.1296 3.0000 24,25,26
Twist Boat Carbon:
# SCF GIAO Magnetic shielding # X-Axis: Shift (ppm) # Y-Axis: Degeneracy # Reference: TMS B3LYP/6-31G(d,p) Chloroform # Reference shielding: 192.17 ppm # NMR Degeneracy Tolerance: 0.05 # # X Y Degeneracy 9-C 219.1346475563 1.0000000000 1.0000000000 4-C 143.9765804972 1.0000000000 1.0000000000 10-C 130.0853002218 1.0000000000 1.0000000000 16-C 94.9347742019 1.0000000000 1.0000000000 17-C 63.7834889940 1.0000000000 1.0000000000 12-C 57.1452497569 1.0000000000 1.0000000000 3-C 51.2487576823 1.0000000000 1.0000000000 5-C 50.5506620746 1.0000000000 1.0000000000 8-C 48.0064934354 1.0000000000 1.0000000000 49-C 45.4690264790 1.0000000000 1.0000000000 48-C 44.1793495095 1.0000000000 1.0000000000 15-C 41.4926294807 1.0000000000 1.0000000000 18-C 33.8519354571 1.0000000000 1.0000000000 11-C 31.8429883667 1.0000000000 1.0000000000 2-C 30.7204558596 1.0000000000 1.0000000000 13-C 28.8173816911 1.0000000000 1.0000000000 1-C 27.9055314209 1.0000000000 1.0000000000 6-C 26.2880518966 1.0000000000 1.0000000000 14-C 23.1472334316 1.0000000000 1.0000000000 7-C 20.3620576844 1.0000000000 1.0000000000

Twist Boat Proton
# SCF GIAO Magnetic shielding # X-Axis: Shift (ppm) # Y-Axis: Degeneracy # Reference: TMS B3LYP/6-31G(d,p) Chloroform # Reference shielding: 31.7462 ppm # NMR Degeneracy Tolerance: 0.05 # # X Y Degeneracy 41-H 5.3715855636 1.0000000000 1.0000000000 19-H 3.4210073533 1.0000000000 1.0000000000 53-H 3.3694278965 1.0000000000 2.0000000000 39-H 3.3280250043 2.0000000000 2.0000000000 52-H 3.2512429242 1.0000000000 2.0000000000 50-H 3.2277036425 2.0000000000 2.0000000000 51-H 3.0339075519 1.0000000000 1.0000000000 40-H 2.7357860947 1.0000000000 1.0000000000 20-H 2.6186809712 1.0000000000 3.0000000000 28-H 2.5739056352 2.0000000000 3.0000000000 43-H 2.5367153866 3.0000000000 3.0000000000 44-H 2.4120744154 1.0000000000 1.0000000000 21-H 2.2609027499 1.0000000000 3.0000000000 35-H 2.2285994845 2.0000000000 3.0000000000 23-H 2.2145523808 3.0000000000 3.0000000000 34-H 2.1531666518 1.0000000000 1.0000000000 32-H 2.0211491788 1.0000000000 1.0000000000 38-H 1.9575063911 1.0000000000 2.0000000000 30-H 1.9477834571 2.0000000000 2.0000000000 33-H 1.6852180000 1.0000000000 1.0000000000 22-H 1.6155498926 1.0000000000 3.0000000000 31-H 1.6108384435 2.0000000000 3.0000000000 Post Averaging: 45,46,47 1.200028666 24,25,26 1.140501877 27,28,29 1.476014127
Asymmetric Epoxidation Reactions
Catalyst Crystal Structures
The crystal structures of enantiomerically pure chiral compounds offer the closest observations the theoretical chemist has to the nature of the 'active' species present in solution; for a catalyst even more so. Presently an investigation of some of the more esoteric aspects of two previously synthesized catalysts (specifically their precatalysts) will be carried out, and the consequences of these for their substrate preferences will be assessed.
Shi's Catalyst
This organocatalyst is based on a protected D-fructose framework, therefore will likely adopt a structure which maximises the anomeric effect[1] about the fused 5- and 6-membered rings. We are concerned with finding a ring conformation in which any carbon-heteroatom bonds α to oxygen are axial, and in which the ring C-O bond exhibits a small amount of double bond character (of course the absolute stereochemistry does not depend on the ring flipping). The most up to date crystal structure recorded[2] confirms the orientations relative to the ring, but one of the molecules present in the unit cell shows the opposite trend with regard to bond lengths (142.0 and 140.5pm for the 'expected' molecule, and 141.5 and 142.3pm for the other - see JMol figure), implying an anomeric interaction arising from the five-membered ring. This may be a packing effect, but the most famous example of mutual anomeric interactions in fused rings, dispiroketals, also show disparate C-O bond length differences within the same molecule (two examples[3][4] of a chemically similar nature and low enough crystallographic R value have been found).
Shi's Catalyst |
An analysis of dihedral angles about the carbon-oxygen bonds in the 2,2-dimethoxypropane rings indicated that they are significantly more planar than has been found in meta-studies before[5], and once again quite different within the unit cell. How much lateral rotation is possible in the regime within which both oxygen atoms are still stereochemically down however is debatable, but probably minimal.
Jacobsen's Catalyst[6]
Proton positions cannot be discerned by X-ray diffraction and so the close approach of the bulky substituents on the salen ligand have been determined by using the carbon distances. Once again the two molecules in the unit cell are nonequivalent as far as their geometrical arrangement, with one's salen system being much more dihedrally twisted (the angle about the base of the pyramid is either 5.3° or 10.7°), necessitating larger butyl-butyl distances (374.5 and 403.7 vs 386.1 and 396.6pm). However this may not be inherently repulsive: Depending on the rotation of the methyl hydrogens this distance could place them in a favourable position for a positive VdW interaction in both cases.
Jacobsen's Catalyst |
The extent of the asymmetry in the catalyst actually appears rather subtle as far as the topology of the metal's surroundings is concerned. There is also an apparent protrusion of the metal away from the ligand towards the chlorine: The C-Mn-C angles measured (where C=ring carbon bound to schiff base unit) are 154.2 and 157.6°, over 20° away from planar. The implications of this for the catalytic activity will be discussed in section 3.2.3
Properties of Synthesised epoxides
Trans-β-methylstyrene oxide (7) has been prepared using both catalysts elucidated above, although significantly more successfully with the former. The expected (R,R) diastereomer[7] of this reaction has been investigated by a variety of quantum mechanical methods to maximise the potential comparison with recorded physical data.
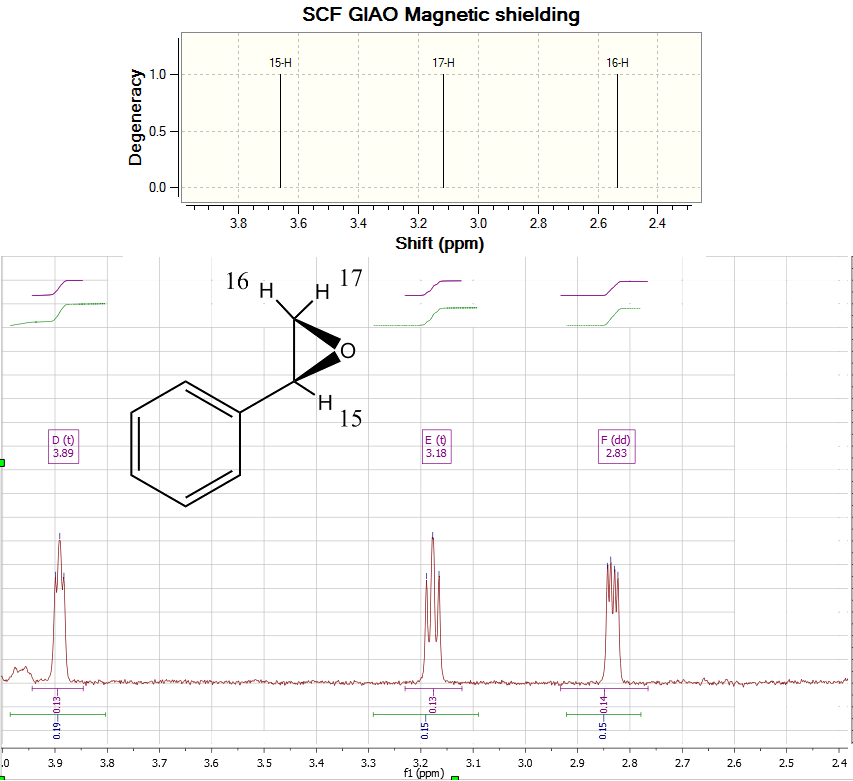
There was little dependence on conformation in the appearance of the NMR spectrum, although the reproduction of the aromatic proton shifts to the literature was surprisingly poor, with them all appearing below 7ppm rather than the known 7.2-7.4[8]. Spin-Spin coupling determination was also done during this calculation[9], and their values were found to be adequately correlated with observations (table below).
| Literature | Observed | Calculated [B3LYP/6311G(d,p)] | Deviation [from observed] | |
|---|---|---|---|---|
| 3JH(20)-H(17-19) | 5.1 | 5.0 | 5.45 | +0.45 |
|
3JH(20)-H(15) |
2.1 | 2.0 | 1.3 | -0.7 |
Optical rotation calculations using a chloroform solvation model initially[10] gave a value 3x too large (133.5 vs 44.3[11] degrees). The basis set was deemed to be too small to provide accurate results and so a larger functional was included; 6-311++G(2df,p) vs the original 6-311++G(d,p). This produced an α value of +41.44[12] , a much better correlation with the range of values reported for the majority product of the reaction over the last 20 years[13][14][15], and so its identity may be concluded to a high level of confidence.
The epoxidation of Styrene has been attempted with Jacobsen's catalyst and only NMR data recorded on the resultant sample produced. It should follow that a B3LYP calculation of a similar nature to that run on 7 should aid in the identification of the sample (no known literature involving non deuterated variants of this compound have been found). The enantiomer (styrene oxide only has one chiral centre) chosen for first calculation[16] was the S, based on the assumption that the ordering of transition state energies would be similar to those for the reaction with trans-β-methylstyrene(see section 3.2.3) and this product would be slightly in excess. The lack of rotational equilibration means that the produced spectrum should correlate exactly (and so may be printed precisely from the logfile).
The results are somewhat better than that for the previous epoxide although there is a consistent under-prediction relative to the observed. Unfortunately, calculations on the R-enantiomer produced the same spectrum to two decimal places[17], and currently no conclusions can be reached with regards to the outcome of this reaction by this treatment.
Transition State Considerations
Returning immediately to styrene-oxide 8, the lowest energy transition state for the Jacobsen epoxidation has been identified and is consistent with a majority S product mixture[18], as expected. The energy difference ΔG between this and the competing lowest energy R transition state[19] is 15.72kJmol-1 (5.988*10-3hartree). The kinetically controlled nature of the reaction tells us that the lowest energy maximum in the reaction profile will define the majority stereochemical outcome. We may now calculate a theoretical enantiomeric excess.
The reaction quotient, K, is given by , where T = 273K for this process. Note that the activation energy is not known, but may be neglected due to the properties of exponentials:
This implies a 99.8% enantiomeric excess; somewhat ambitous. It must be stated though that this model does not take a large number of possibilities into account, including:
- other reaction pathways, including those occurring via the other computed transition states
- intermediates in which stereochemistry is lost by rotation through a radical intermediate[20]
- reactions which proceed to the transition state and then fall back down to the reactants
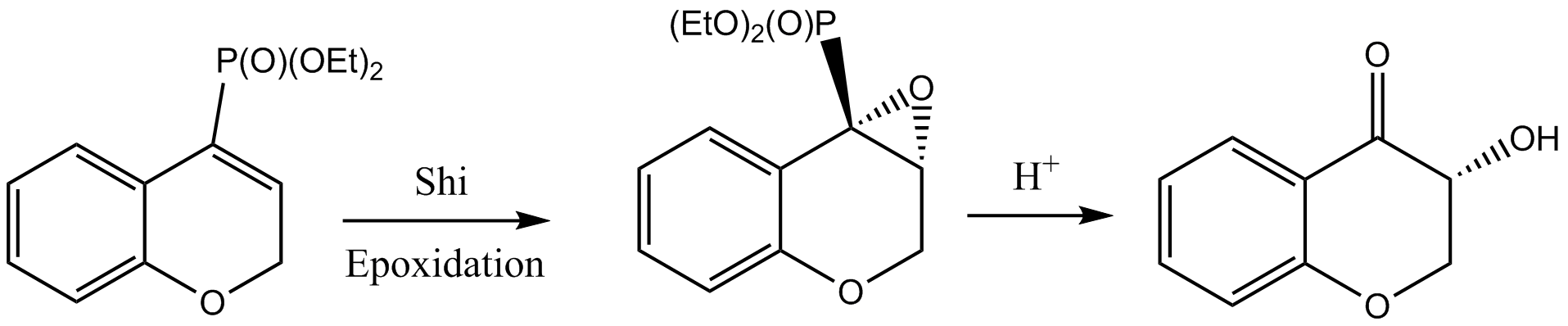
So we can see that rather simple modelling of the reaction pathway (reactant > TS > product) allows the extraction of useful information about the outcome (provided high level calculations have been conducted) that cannot be extracted from the simulation of experimentally observable properties. Presently two computational methods will be employed to analyse the transition states invisaged for two other epoxidation reactions, namely noncovalent interactions (courtesy of wB97X-D density functional theory[21] calculations) and Quantum Theory Atoms In Molecules (QTAIM) (which provides information on saddle points in electron and nuclear density[22]).
The most stabilised transition state has been isolated from the possible permutations relating the reaction of the dioxirane derivative of Shi's catalyst 5 with one molecule of trans-β-methylstyrene. It consists of a spiro orientation of the alkene about the 'up' oxygen of the oxirane, en route to the formation of the (R,R) diastereomer. Attempts will now be made to identify the stabilisations incurred in this transition state (and that of the corresponding Jacobsen reaction) responsible for the energetic result.
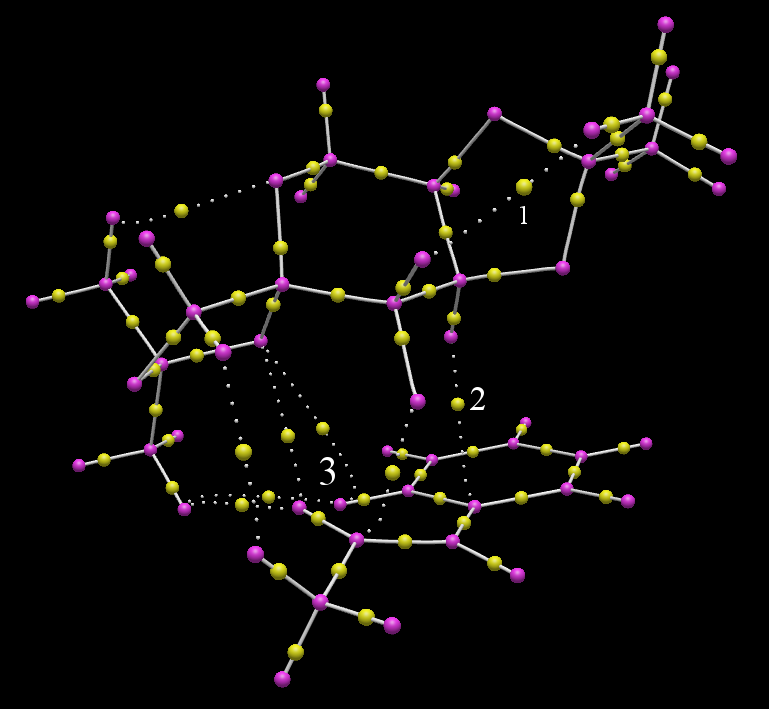
QTAIM treatment allows one to gain a more precise appraisal of where bonds are and how electron density is shared relative to that usually supplied by programs which interpret atomic and molecular coordinates. In the previously considered example the only reorganisation of bonds present that actively drives the reaction relative to the starting materials are the 'opening' of the dioxirane and the formation of a carbon oxygen bond to the β carbon of the alkene. In this sense it is a quite early transition state, although the aforementioned C-O bond critical point is ostensibly in between the two olefin carbons, perhaps implying the 'decision' of which carbon to add to first occurs quite soon before it. Nonetheless, the bulk of the electron density sharing that would appear to stabilise arises from much less conspicuous interactions:
- The formally less than two coordinate dioxirane oxygen (that will become the cabonyl at the completion of the reaction) forms a hydrogen bond 1 to the methyl of the protected ring.
- An axial fructose hydrogen forms some kind of electron sharing interaction 2 with the phenyl it is directly above (likely donation from π orbitals)
- Hydrogens 7 and 20 (from the numbering in figure 5) interact strongly with several atoms on the spirocyclic 5-membered ring, namely the methyl hydrogens and anomeric oxygen. This is the only 'bonding' process that is unique to this molecular orientation and is believed to be the effect most responsible for (R,R) being the majority product
- Interestingly, the bottom of the well 3 around hydrogen 7 does not coincide with the nuclear critical point; it deviates considerably towards the ring.

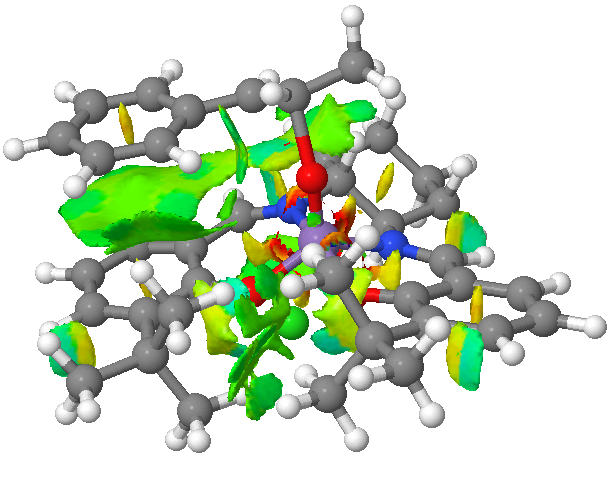
Noncovalent interactions were deemed to be a more useful approach to evaluate the Jacobsen epoxidation of trans-β-methylstyrene, (a reaction that occured with surprisingly low yield and selectivity when carried out by the author). The method was chosen due to the large, planar nature of the catalyst in comparison to Shi's, which was thought to favour point like interactions better.
Although there is very little energetic benefit between enantiomers, the lowest energy transition state has been found as an (S,S) forming one, specifically resulting from a leftward approach (if oxygen is placed up and the tert butyl groups forward). This is known as the Φ= -90 approach, and has been identified previously as a minimum in energy[23]. As was expected, there exists a large noncovalent surface linking the ring of the catalyst and the ring of the alkene. The positioning of the chloride ion, which initially might appear arbitrary, can be seen to be entirely justified by a cradle of attractive forces arising around the schiff base section of the catalyst.
This alone does not account for the lack of observed reactivity however. Finding any significant energetic penalties in this transition state would prescribe a worse fate for any possible others and might go some way to explaining the poor results: One immediate contender is the large number of unsatisfactory clashes between the atoms immediately bonded to Manganese. These, taken simultaneously with the distortion at the metal away from its preferred square pyramidal coordination signifies a significant penalty. They are probably not semi-covalent or bond-forming in nature and it is speculated that they would be alleviated by the absence of the methyl group above the metal/cyclohexane ring. This may therefore illustrate the propensity for Jacobsen's catalyst to selectively form cis epoxides (even from trans substrates, due to an aforementioned radical intermediate20), and simultaneously explains the planarity of the precatalyst noted from the crystal structure.
References
- ↑ J. A. Kanters, G. Roelofsen, B.P. Alblas, I. Meinders, Acta. Cryst. B., 1977, 33, 665
- ↑ Z.X. Wang, S.M. Miller, O.P. Anderson, Y. Shi, J. Org. Chem., 2001, 66(2), 521
- ↑ A.J.Blake, R.O.Gould, R.M.Paton, C.J.Todd, Acta. Cryst. C., 1997, 53, 116
- ↑ M.G.Banwell, A.J.Edwards, M.Essers, K.A.Jolliffe, J. Org. Chem., 2003, 68, 6839
- ↑ A. Cosse-Barbi, J.E. Dubois, J. Am. Chem. Soc., 1987, 109, 1503
- ↑ J.W.Yoon, T.S.Yoon, S.W.Lee, W.Shin, Acta. Cryst. C., 1999, 55, 1766
- ↑ Y. Shi, H. Tian, X. She, L. Shu, H. Yu, J. Am. Chem. Soc., 2000, 122, 11551
- ↑ Z.X. Wang, L. Shu, M. Frohn, Y. Tu, Y. Shi, Org. Synth., 2003, 80, 9
- ↑ S. Ingram, 2014, DOI:10042/27446
- ↑ S. Ingram, 2014, DOI:10042/27448
- ↑ O.A. Wong, B. Wang, M.X. Zhao, Y. Shi, J. Org. Chem., 2009, 74(16), 6335
- ↑ S. Ingram, 2014, DOI:10042/27449
- ↑ P. Besse, M.F. Renard, H. Veschambre, Tetrahedron Asymmetry, 1994, 5(7), 1249
- ↑ A. Archelas, R. Furstoss, S. Pedragosa-Moreau, Tetrahedron, 1996, 52(13), 4593
- ↑ D. Chen, B. Nettles, Y. Shi, B. Wang, O.A. Wong, X.Y Wu, M.X. Zhao, J. Org. Chem., 2009, 74(10), 3986
- ↑ S. Ingram, 2014, DOI:10042/27463
- ↑ S. Ingram, 2014, DOI:10042/27469
- ↑ H. Rzepa, 2013, DOI:10.6084/m9.figshare.860441
- ↑ H. Rzepa, 2013, DOI:10.6084/m9.figshare.860449
- ↑ M. Palucki, N.S. Finney, P.J. Pospisil, M.L. Güler, T. Ishida, E.N. Jacobsen, J. Am. Chem. Soc., 1998, 120, 948
- ↑ J.D. Chai, M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615
- ↑ R.F.W. Bader, in Atoms in Molecules - A Quantum Theory ,Oxford University Press, 1990
- ↑ H. Jacobsen, L. Cavallo, Chem. Eur. J., 2001, 7(4), 800
Supplementary Information
S-Styrene-oxide 1H NMR
# SCF GIAO Magnetic shielding # X-Axis: Shift (ppm) # Y-Axis: Degeneracy # Reference: TMS B3LYP/6-31G(d,p) Chloroform # Reference shielding: 31.7462 ppm # NMR Degeneracy Tolerance: 0.05 # # X Y Degeneracy 12-H 7.5145681226 1.0000000000 4.0000000000 6-H 7.5126918999 2.0000000000 4.0000000000 1-H 7.4834731128 3.0000000000 4.0000000000 4-H 7.4464269090 4.0000000000 4.0000000000 8-H 7.2986346277 1.0000000000 1.0000000000 15-H 3.6625777185 1.0000000000 1.0000000000 17-H 3.1154716746 1.0000000000 1.0000000000 16-H 2.5354715237 1.0000000000 1.0000000000
R-Styrene-oxide 1H NMR
# Summary of NMR spectra (SCF GIAO Magnetic shielding)
# Values for element H only
# Reference: TMS B3LYP/6-31G(d,p) Chloroform
# Reference shielding: 31.7462 ppm
# Degenerate peaks are condensed together (Degeneracy Tolerance 0.05)
#
# Shift (ppm) Degeneracy Atoms
7.4893044466 4.0000 1,8,4,6
7.2978507323 1.0000 10
3.6625534004 1.0000 15
3.1139900444 1.0000 16
2.5339504875 1.0000 17
(R,R) Trans-β-methylstyrene oxide 1H NMR
# SCF GIAO Magnetic shielding # X-Axis: Shift (ppm) # Y-Axis: Degeneracy # Reference: TMS B3LYP/6-31G(d,p) Dichloromethane # Reference shielding: 31.7445 ppm # NMR Degeneracy Tolerance: 0.05 # # X Y Degeneracy 11-H 6.8777556427 1.0000000000 4.0000000000 9-H 6.8586957938 2.0000000000 4.0000000000 10-H 6.8331397590 3.0000000000 4.0000000000 12-H 6.8006612080 4.0000000000 4.0000000000 7-H 6.6096918235 1.0000000000 1.0000000000 15-H 2.9506539020 1.0000000000 1.0000000000 20-H 2.3985627503 1.0000000000 1.0000000000 17-H 1.1805834394 1.0000000000 1.0000000000 19-H 1.0757768047 1.0000000000 1.0000000000 18-H 0.2682955496 1.0000000000 1.0000000000 Post Averaging: 17,18,19 0.8415519309
Suggestions for further Investigations
The suggested epoxide has been found to decompose extremely quickly in the presence of aqueous acid to produce the ketone below and is actually not isolable as a result[1]. The reasons for this may be worthy of computational modelling, and indeed might introduce the need for more complex functionals as the epoxide molecule contains a phosphorus atom. Nevertheless, this resultant ketone is an extremely likely candidate for an incorrect assignment as Krawczyk et. al. recorded a negative optical rotation (α= -8.8°), but the compound as drawn (presumably the favoured Shi product) is the (+) enantiomer, with a known[2] α of +54°.