Rep:Mod:Loftus
Background
Computational chemistry has been used since the early 1940's to solve complex chemical problems. It has proven itself to be an extremely successful approach by reducing both the cost and time constraints of trial and error synthesis. This makes it a valuable tool for many chemists to use in modern day techniques.
Analysing the Hydrogenation of Cyclopentadiene Dimers
Introduction
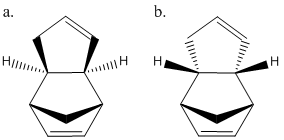
A molecular mechanics approach was first used to compute the relative stability of two cyclopentadienes dimers a and b, by minimizing their energies. The stability of the two products from the hydrogenation of the endo (a) dimer were then calculated to see which is preferably formed.
The use of molecular mechanics for this approach although less accurate than some other MO based techniques is suitable due to the dimers only containing carbon and hydrogen atoms which are well defined and hence yield good approximations. MM2 force fields were used for this calculation as they are known to provide good accuracy for hydrocarbon based molecules as they rely on previously computed data from similar molecules.
Results/Discussion
The results of the energy minimisation shows that product a has a final energy which is lower than that of b by 2.12 kcal/mol. This means that a is the more stable conformation and hence the thermodynamic product, making b the kinetic product.
| Molecule | Energy / kcal mol-1 |
|---|---|
| a | 31.88 |
| b | 34.00 |
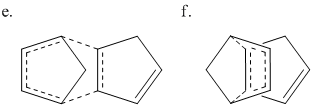
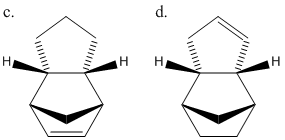
The two products form from the dimerisation of cyclopentadiene in a 4π+2π Diels-Alder cycloaddition reaction. This can occur from two transition states shown in Fig. 3 leading to the two possible products c and d.
Even though the exo product is thermodynamically more stable, the endo dimer predominates due to it having a more stable transition state, caused by better orbital overlap during the transition state. This effect is known as the "endo addition rule".
The energy minimisations from the hydrogenation of the endo product show that it is more preferable to hydrogenate the double bond on the pentyl ring rather than the cyclohexene bond. This is evident from the energy difference of 20.53 kcal/mol. Again this shows that product d is the thermodynamic product while c the kinetic.
| Molecule | Energy / kcal mol-1 |
|---|---|
| c | 35.69 |
| d | 31.15 |
If we look more specifically at the contributions to the final energy we see that the main difference is in the bending term which is ~5 kcal/mol larger for c showing that the removal of the double bond in this example has a large effect on the overall energy.
| c | d | |
|---|---|---|
| Contribution | Energy / kcal mol-1 | Energy / kcal mol-1 |
| Stretch | 1.28 | 1.10 |
| Bend | 19.87 | 14.53 |
| Torsion | 10.81 | 12.50 |
| 1,4 VDW | 5.63 | 4.51 |
Conclusion
From the computational analysis we can see that a the endo product and d, are both thermodynamically preferred as there is less strain on the molecules giving them lower energies than the other products.
Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)
Introduction
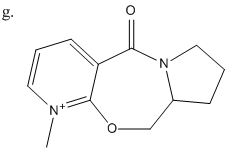
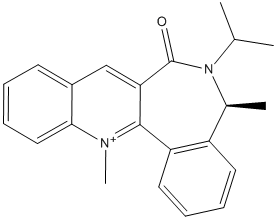
Again using molecular mechanics the steriospecific reaction shown in Fig 6. was analysed. The energy of structure g was analysed, this time using the MMFF94 force fields in preference to MM2, as they are more suited to larger molecules, as in this case. The MeMgI cannot be modelled as part of the structure as the molecular mechanics approach does not extend to Mg.
Using the results from the analysis of g and some other data the steriospecifity of the reaction of h and PhNH2 shown in Fig 7. was also investigated.
Results
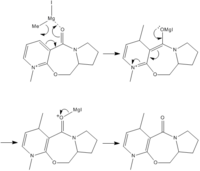
The results of the energy minimisation is shown in table 4 and the corresponding 3D structure can be viewed in Fig 4. Each minimisation was carried out between 3 and 5 times to ensure that the lowest energy configuration was found.
| Product | Energy / kcal mol-1 | Dihedral angle |
|---|---|---|
| g | 57.47 | 17.6 |
From the reaction mechanism and the dihedral angle between the C=O and pyridine ring (planar) which is shown more clearly in Fig 4. It was seen that the selectivity arises due to the initial co-ordination of the magnesium to the carbonyl. The reaction that then takes place is restricted to the same face that the carbonyl group is on, giving the specific steriochemistry.
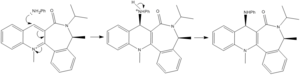
The energy minimisation and dihedral angle between the carbonyl and ring of h was found to be.
| Product | Energy / kcal mol-1 | Dihedral angle |
|---|---|---|
| h | 98.40 | 38.0 |
In this example, the dihedral angle is larger than before, showing that the carbonyl group is bent to a greater degree. However, unlike last time there is no co-ordination in the reaction mechanism and therefore the amine can attack from the least hindered side. This being the one opposite to the carbonyl, as the lone pair on the nucleophilic nitrogen will be repelled by the two lone pairs of oxygen on the carbonyl. The large phenyl group will also contribute to the steriochemistry of the preferred attack due to steric hindrance between the phenyl and the carbonyl group. Taking these to effects into account shows that the preferred steriocontrol of the reaction is that shown in Fig 7.
Conclusion
The conformations of each reactant g and h obtained from energy minimisations, when combined with considerations of the reaction mechanisms show that steriocontrol of each reaction is due to firstly , the co-ordination of magnesium "guiding" g to react on the face shown, and in the case of h, the repulsion of lone pairs on both nitrogen and oxygen combined with the steric hindrance of the phenyl ring.
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
Introduction
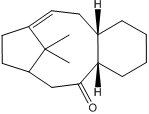
The intermediate in the synthesis of taxol shown in Fig 8. is initially formed as two isomers with the carbonyl pointing up or down. Given time, the compound spontaneously isomerises to form the most stable isomer exhibiting atropisomerism. By minimising the energy of the two isomers (carbonyl up or down) using both MM2 and MMFF94 force fields for comparison, the most stable form was found. The slowness of the alkene functionalisation was then also explored.
Results/Discussion

The results of the energy minimisations shown below indicate that having the carbonyl group pointing down (j) is the most stable form. This is as would be predicted by reasonable deduction because it minimises both the sterics from being close to the two methyl groups on top of the ring system and the two hydrogens which also point upwards. The energy difference between i and j for the MM2 calculations is ~10 kcal/mol while for MMFF94 it is ~15 kcal/mol this is relatively small and is most likely sue to the differences in force fields which are in use.
| MM2 | MMFF94 | |
|---|---|---|
| Molecule | Energy / kcal mol-1 | Energy / kcal mol-1 |
| i | 53.02 | 76.44 |
| j | 43.31 | 61.04 |

The reaction of the alkene is slow due to it being hyperstable. The hyperstability comes from the fact that when the alkene is hydrogenated, the products strain increases as opposed to the more normal and expected decrease in energy, known as negative olefin strain energy.[3] This is shown by the MM2 energy minimisations of i and k, where k is the hydrogenated product.
| Molecule | Energy / kcal mol-1 |
|---|---|
| i | 53.02 |
| k | 61.41 |
A possible reason for the alkene being hyperstabilised is due to attractive VDW interactions between the hydrogens on either side of the alkene which were measured to be 2.32 Å and 2.35 Å apart, these are in the correct region for this type of attraction (~2.4 Å). Fig 10. illustrates the distances and hydrogens discussed.
Conclusion
Using two molecular mechanics force field sets (MM2 and MMFF94) the lowest energy form of the taxol intermediate was found to be with the carbonyl pointing downwards away from both the hydrogens and methyl groups. The alkene was also found to be hyperstable by further energy minimisations showing that the alkane product had a higher energy than alkene. VDW attraction between the hydrogens was a possible explanation for this.
Modelling Using Semi-empirical Molecular Orbital Theory
Introduction
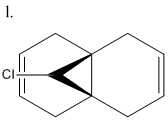


The reaction of molecule l (Fig 11.) with dichlorocarbene shows particular selectivity in forming the mono adduct (m) (syn), in preference to the di adduct (n).[4] This type of selectivity can only be effectively explained using a molecular orbital approach.
To do this energy minimisation of l using MM2 was carried out giving a value of 17.89 kcal/mol. The energy was then minimised again using the MOPAC/RM1 MO method and then the molecular surfaces calculated again using MOPAC/RM1. From the calculated MO's the selectivity of the reaction shown in Fig 12. can be explained.
The carbon chlorine bond effect on the rest of the molecule was then investigated further by comparing the C-Cl and C=C vibrational frequencies of l and the product from the hydrogenation of the anti alkene (Fig 13.)
To calculate the vibrational frequencies a density functional approach was used, where the optimised structures of each l and ? were minimised using MOPAC/RM1 and then submitted to Gausssian for frequency optimisation.
Results/Analysis
The MO's calculated using MOPAC/RM1 are shown below. The HOMO is the most important MO in affecting the reactivity as it will be most reactive to electrophilic attack. Looking at the HOMO we can see that there is far greater electron density on the alkene that is on the same side as the chlorine (syn) making it very nucleophilic. In the reaction mechanism dichlorocarbene acts as a electrophile and will therefore be more likely to react with an area of high electron density. Taking both into account it is clear that the selectivity of the reaction comes from the dichlorocarbene favouring reacting with the more nucleophilic alkene.
There is also the possibility of a further stabilisation from antiperiplanar overlap of the LUMO+2 orbital with the HOMO-1 which further helps to favour product m as it makes the anti alkene slightly more stable.[5]
| HOMO-1 | HOMO | LUMO |
|---|---|---|
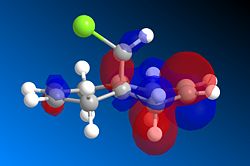 |
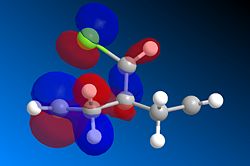 |
 |
Vibrational Frequency
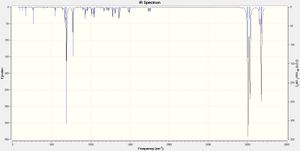
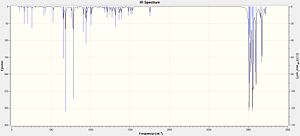
The results of the geometry optimization and frequency anaylsis are tabulated below. The corresponding IR spectrum are shown right.
| di alkene (l) | mono alkene (o) | |||
|---|---|---|---|---|
| Freq / cm-1 | Intensity | Freq / cm-1 | Intensity | |
| C-Cl | 770.86 | 130.06 | 780.03 | 109.24 |
| C=C syn | 1757.34 | 8.94 | 1753.72 | 11.47 |
| C=C anti | 1737.04 | 9.64 | na | na |
Starting with l, the C-Cl stretch is found in the correct region and agrees extremely well with literature value of 600-800 cm-1.[6] The values of the two C=C stretches, however, are high when compared to the literature value of 1620-1680 cm-1. [7] An increase in the calculated frequency of absorption, corresponds to absorption at a lower wavelength (λ=1/freq) which will have a higher energy (E=hc/λ). This shows that the bond requires more energy to cause a vibration indicating that it must be stronger than a normal C=C bond. A possible reason for the increase in strength could be from the effect of the Cl atom causing a stabilising effect on the double bond or the fact that the alkene is in a constrained cyclic system. It could also be due to slight inaccuracies of the gaussian optimisations and calculations.
The difference in the values of the two C=C bonds on l shows that the syn alkene has a higher frequency stretch compared to the anti alkene. Using the same explanation as above, this shows that the bond is slightly weaker which helps to explain why this alkene is more reactive than the anti alkene, shown by the 72:23 % product ratios. However, this does somewhat contradict the information from the MO's shown in Fig 14-16. as the HOMO shows more electron density on the syn side indicating that it would be stronger than the anti alkene. Other interactions between orbitals must therefore contribute to the weakening of the syn alkene or strengthening of the anti alkene.
The values of the C-Cl stretch in o also agrees well with literature, being in the correct region. The C=C value is again high compared to literature and it is possible that this could be due to the same explanations which have already been given.
Comparing the C-Cl values between l and o shows that the mono alkene's stretch is at a slightly higher frequency. A slight weakening of the bond could be from the loss of the second alkene which was stabilising the bond. The syn alkene bond stretch frequency is slightly lower for the mono alkene (o) the difference is only small ~4 cm-1 and could be attributed to the decrease in strain on the bond from the removal of the other double bond and overall lowering in energy of the molecule.
Conclusion
The selectivity of the reaction shown in Fig 12. was attributed to the chlorine causing the greater electron density on the syn alkene which intern caused the electrophilic carbene to favour reacting with the syn rather than anti alkene. This was shown by looking at the HOMO of l where the increased electron density was visible.
The vibrational analysis has shown that there is indeed a difference in the two C=C bonds as they have different IR stretches within the same molecule (l) backing up the with the syn bond shown to be weaker and hence more reactive contributing to the higher yield of the mono adduct. It also showed small differences in thevalues of the C-Cl bond between l and o and in the frequency of the syn C=C of l and o.
Structure based Mini project using DFT-based Molecular orbital methods
Introduction

The aim was to investigate the observed diastereoselectivity of a Diels-Alder reaction between maleic anhydride and a particular chiral (9-anthryl)carbinol (p). The reaction scheme is shown in Fig 19. This reaction gives extremely good selectivity of the r product in preference to the s product.
The C13 NMR of the main product r and also the minor product s were calculated using gaussian and compared with the literature values to see if there was good agreement between the literature results main product, and the computational equivalent.
To compute this, the predicted product was first minimised using MM2 force field to give the general structure. It was then minimised again using the MOPAC/PM6 method. The resulting structure was then outputted to gaussian for further minimisations at the mpw1pw91/6-31g(d,p) level. After this final stage of optimization the structure could again be submitted to gaussian for NMR chemical shift calculation, using the mpw1pw91/6-31(d,p) method again and setting the solvent to chloroform, as it is stated in the literature.
To account for the possible selectivity the reaction mechanism and conformation of the reactants were taken into account.
Results/Analysis
To determine between the two products r and s the main methods which could be used would be x-ray crystallography as it would show the distance and angles between the chiral atoms and the atoms on the five membered ring showing which side the ring was on and hence which orientation it had when reacting. From the data, the solid is non crystalline and hence, a different method was needed to determine the steriochemistry of the product.
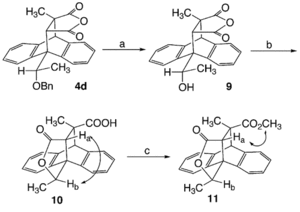
The method used was to transform the product into a lactone, and then using NOE's look at the relationship between the syn hydrogens. This is shown clearly by Fig 20. with syn hydrogens Ha and Hb as the reaction to form the lactone retains specific steriochemistry relating to the reactant.
C13 NMR Comparison
The results of the caluclated C13 NMR for r are tabulated below, along with the literature values for r. The results of the computation of the NMR of s have also been tabulated and again the difference from the literature values shifts of r.[9][10]
| C13 / ppm | |||||
|---|---|---|---|---|---|
| Product r | Product s | ||||
| Carbon # | Literature | Calculated | Difference | Calculated | Difference |
| 34 | 170.5 | 171.1 | 0.6 | 171.8 | 1.3 |
| 37 | 169.4 | 171.0 | 1.6 | 171.5 | 2.1 |
| 5 | 141.9 | 143.4 | 1.5 | 141.1 | 0.8 |
| 4 | 138.6 | 142.1 | 3.5 | 138.4 | 0.2 |
| 9 | 138.4 | 139.8 | 1.4 | 140.1 | 1.7 |
| 8 | 138.0 | 139.3 | 1.3 | 142.5 | 2.5 |
| 6 | 127.5 | 128.6 | 1.1 | 124.9 | 2.6 |
| 12 | 127.4 | 127.1 | 0.3 | 126.7 | 0.7 |
| 2 | 127.0 | 126.9 | 0.1 | 127.3 | 0.3 |
| 14 | 126.8 | 126.7 | 0.1 | 128.0 | 1.2 |
| 1 | 126.3 | 126.3 | 0.0 | 126.5 | 0.2 |
| 13 | 125.5 | 126.3 | 0.8 | 126.1 | 0.6 |
| 11 | 124.0 | 125.9 | 1.9 | 124.4 | 0.4 |
| 3 | 123.9 | 123.4 | 0.5 | 125.3 | 1.4 |
| 15 | 73.5 | 78.7 | 5.2 | 76.8 | 3.3 |
| 10 | 57.2 | 60.9 | 2.8 | 56.7 | 0.5 |
| 24 | 54.6 | 57.7 | 3.1 | 56.5 | 1.9 |
| 22 | 49.7 | 56.7 | 7.0 | 54.8 | 5.1 |
| 33 | 48.3 | 55.0 | 6.7 | 61.3 | 13.0 |
| 7 | 46.4 | 52.1 | 5.7 | 52.2 | 5.8 |
| 16 | 16.7 | 21.2 | 4.5 | 26.2 | 9.5 |
| Sum | 45.2 | Sum | 55.1 | ||
In general, the computed C13 NMR of r agrees well with the literature values, especially at the higher shifts where the differences are very small. It does however become less accurate at lower shifts indicating that the geometry could be slightly wrong in these areas, leading to the differences.
The NMR of s if also compared to the supposed literature values for r are also similar in some areas, this would be expected as much of the molecule is very similar. It also shows deviation from the literature values at lower shifts, although in this case they are to a much larger degree. Specifically for example C33 which has a difference of 13 ppm and C16 where the difference is 9.5 ppm.
The overall differences in NMR shifts which have been calculated (Sum=) does favour the fact that the correct product is r as indicated by the paper, and not s, which was expected and fits well. More specifically the small changes which we might expect in C34, C16, C33 shifts from having different position relative to other carbons caused by the different conformations of the two products is also strongly in favour of r as its calculated shifts are all closer with respect to the literature.
Although there are some differences larger than 5 ppm between the calculated spectrum of r and the literature values, I believe these conformations are very close to correct. The differences could be the result of a very small change in the conformation of the more mobile OMe and Me group on the chiral carbon as these are generally the values which are furthest from literature. I do not believe that the differences are large enough to constitute the wrong steriochemistry of the product, only the fact that the NMR calculation is very sensitive to small deviations.
Mechanism

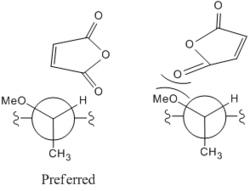
The two possible products are formed due to the different alignments of the maleic anhydride above the planar ring system as shown in Fig 22. These then cause the transition states shown to form and each steriospecific product to form.
By minimising the energy of each of the products using simple MM2 force fields we can see that r is the kinetic product and s the thermodynamic. This can be seen from the energy of s being lower than r, however we know that the reaction is highly specific about producing r.
| Molecule | Energy / kcal mol-1 |
|---|---|
| r | 57.60 |
| s | 49.92 |
The best explanation of the high selectivity of r over s for this reaction is due to the steric hinderance from the maleic anhydride carbonyls clashing with the OMe group on the chiral carbon as shown in Fig 23. As the maleic anhydride aligns the carbonyls would be in close proximity to the OMe group and both steric hinderance between the two groups would make it unfavourable. Instead the maleic anhydride aligns with the hydrogen which is far smaller and less sterically demanding making it more likely to react in this conformation. This conformation also maximises σ donation which will further stabilise the transition state.
This explanation was further strengthened by another reaction which is carried out in7 where the OMe group is replaced by and alchol. With this change, the selectivity reversed forming more of the equivalent of s and makes sense with our theory as possible hydrogen bonding between the carbonyl and the OH group could stabilise the transition state.
As the Diels-Alder reaction takes place, the groups on the chiral carbon rotate anticlockwise, this moves the largest group furthest away (OMe) forming the specific steriochemsitry shown in Fig 19. When the reaction is complete, the chiral carbon cannot rotate due to the non reversible position of the five membered ring and the clashing which would result should they be forced to eclipse. Also any further rotation only make the molecule less stable by moving the larger OMe group closer to the five membered ring.
Conclusion
The selectivity of the reaction shown in Fig 19. is best explained in terms of steric hinderance between the carbonyl on the maleic anhydride and the large OMe group causing r to be almost completely favoured.
After computational analysis of r including minimisation using gaussian and calculations of the C13 NMR there was largely agreement that r was indeed the product formed as there was close matching between the spectrum.
References
- ↑ A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chemistry, 1986, 51, 838.
- ↑ S. Leleu, C. Papamicael, F. Marsais, G. Dupas, V.; Levacher, Vincent. Tetrahedron: Asymmetry, 2004, 15, 3919-3928.
- ↑ P. Camps, F. Perez, S. Vazquez. Tetrahedron, 1997, 53, 9727-9734.
- ↑ B. Halton, S. G. G. Russell. J. Org. Chem., 1991, 56, 5553-5556.
- ↑ B. Halton, R. Boese, H. S. Rzepa. J. Chem. Soc., 1992, 447-449.
- ↑ http://www2.ups.edu/faculty/hanson/Spectroscopy/IR/IRfrequencies.html
- ↑ http://www2.ups.edu/faculty/hanson/Spectroscopy/IR/IRfrequencies.html
- ↑ A. Sanyal, J. K. Snyder Org. Lett., 2000, 2 16, 2527-2530. (http://pubs.acs.org/doi/full/10.1021/ol006206m)
- ↑ A. Sanyal, J. K. Snyder Org. Lett., 2000, 2 16, 2527-2530. (http://pubs.acs.org/doi/full/10.1021/ol006206m)
- ↑ A. Sanyal, J. K. Snyder Org. Lett., 2000, 2 16, (Supplement). (http://pubs.acs.org/doi/suppl/10.1021/ol006206m/suppl_file/ol006206m_s.pdf)
