Rep:Mod:Lkb110
Module 2: Bonding analyses using Ab initio and Density functional techniques
Introduction
Gaussian 5.0 is a valuable tool for the study of molecular structures. It enables the calculation of equilibrium bond lengths, angles, MOs and energies, contributing to the understanding of why certain molecules adopt certain conformations.
Optimisation Comparison
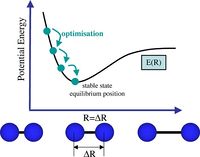
By optimising a molecule, we are calculating the structure that sits at the minimum energy point at the bottom of the PES well, ie equilibrium bond distance r0, where there is an equilibrium between the repulsive and attractive forces present between the nucleus and the electrons.The graph below [1] shows how by optimising we are looking for the distance where the gradient is zero and the potential energy is minimised.
Optimisation of BH3 using 3-21G Basis Set
The trigonal planar BH3 model was built on Gaussian with a point group of D3H. The B-H bond lengths were extended to 1.5 angstroms to aid the accuracy of the calculation.
A lower basis set, 3-21g, was used to give an estimate of the minimum location on the PES, where the molecule is optimised. A higher basis set will then be used to provide greater accuracy.
The calculation was run through Gaussian and the output recorded in a log file linked here: Media:BH3_AT_321G.LOG.
A summary of calculation, provided by Gaussian, is presented in the table below:
| File name | BH3_AT_321G |
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 3-21G |
| E(RB3LYP) | -26.46226435 a.u. |
| RMS Gradient Norm | 0.00003117 a.u. |
| Dipole Moment | 0 (Debye) |
| Point Group | D3H |
| Job cpu time | 0 days 0 hours 0 minutes 4.0 seconds |
The "real" text based .log file allows us to check the convergence has been successful by checking the final set of forces and displacements shown below.
Item Value Threshold Converged?
Maximum Force 0.000062 0.000450 YES
RMS Force 0.000041 0.000300 YES
Maximum Displacement 0.000243 0.001800 YES
RMS Displacement 0.000159 0.001200 YES
Predicted change in Energy=-2.225689D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1945 -DE/DX = -0.0001 !
! R2 R(1,3) 1.1945 -DE/DX = -0.0001 !
! R3 R(1,4) 1.1945 -DE/DX = -0.0001 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The "YES" answers in the "converge" colomn confirm that the data has converged and the calculation has been successful.
Therefore, the following information was collected:
| Final Energy | -26.46226435 a.u. |
| B-H Bond Length | 1.19447 Å |
| H-B-H Bond Angle | 120 degrees |
The images below show the optimisation steps that took place during the calculation. The images are labelled 1, 2 ,3, 4 and 5 in order in which they were considered, where 5 is the final optimised structure, which can be viewed more clearly by clicking on this button
The absence of bonds in image 1 and 2 is due to the distance exceeding a predetermined value. The bonds still exist but they are not graphically represented.
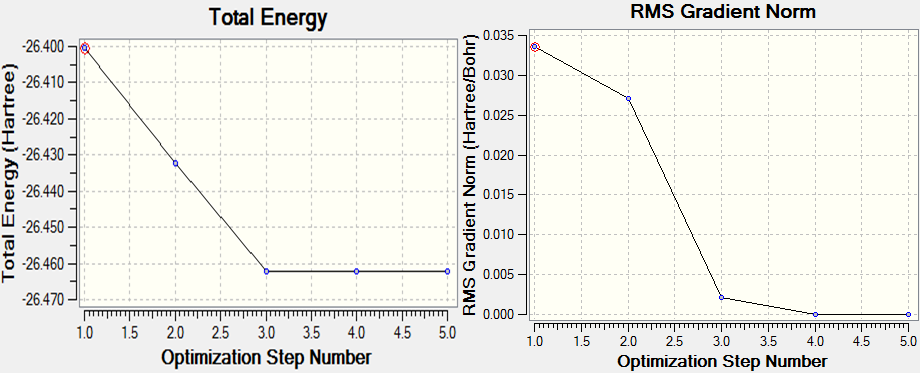
The images coincide with points on the following graphs. It shows that by marginally decreasing the distance between the Boron atom and the Bromine atoms, the Total Energy decreases until it reaches the minimum energy. signifying the potential energy minimum has been reached and therefore so has the optimised, equilibrium bond length. The graph RMS gradient graph shows the change in the Root Mean Square (RMS) gradient as the PES is traversed. It decreases until it is very close to zero, signifying that the structure very close to the equilibrium position where the gradient equals zero.
Optimisation of BH3 using 6-31G(d,p) Basis Set
Having found a rough estimate of the optimised structure using a lower basis set,321G the equilibrium B-H bond length can be honed by the use of a higher level basis set, 6-31G(d,p).
Using the output from the previous BH3 calculation as the input for this calculation, the calculation was run through Gaussian.
The resulting calculation output was recorded in a log file linked here: Media:BH3 AT 631G.LOG.
The summary of the calculation provided by gaussian is tabulated below:
| File name | BH3_AT_631G |
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -26.61532363 a.u. |
| RMS Gradient Norm | 0.00000461 a.u. |
| Dipole Moment | 0 (Debye) |
| Point Group | D3H |
| Job cpu time | 0 days 0 hours 0 minutes 8.0 seconds |
The "real" text based .log file allows us to check the convergence has been successful by checking the final set of forces and displacements shown below.
Item Value Threshold Converged?
Maximum Force 0.000009 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.000036 0.001800 YES
RMS Displacement 0.000024 0.001200 YES
Predicted change in Energy=-5.033874D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1923 -DE/DX = 0.0 !
! R2 R(1,3) 1.1923 -DE/DX = 0.0 !
! R3 R(1,4) 1.1923 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The "YES" notations in the "Converged?" colomn signify that convergence has occured and the calculation was successful.
The following data was collected:
| Final Energy | -26.61532335 a.u. |
| B-H Bond Length | 1.19189 Å |
| H-B-H Bond Angle | 120 degrees |
Summary of 3-21G and 6-31G(d,p) Optimisations
| 3-21G BH3 Optimisation | 6-31G(d,p) BH3 Optimisation | |
|---|---|---|
| Optimised Bond Length (angstroms) | 1.19349 | 1.19189 |
| Optimised Bond Angle (degrees) | 120 | 120 |
| Total Energy (a.u.) | -26.46226338 | -26.61532335 |
The Energy difference between the total energies is 401.86kJ mol^-1.
However, these energies are not comparable because they are dependent on the basis set used.
It can be said that the 6-31G(d,p) data is likely to be closer to the exact values associated with the equilibrium bond length of B-H due to the higher quality of the basis set used.
As a comparison, the literature value of B-H is 1.19001 Å [2] which confirms that the 6-31G(d,p) has given a more accurate prediction of the ultimate BH3 structure.
Optimisation of TlBr3 molecule using the HPC system
To study the use of pseudo-potentials, which increase the ease of calculation, we must carry out the calculation on a heavier atom/molecule. They enable the study of atoms with large numbers of electrons and do not effect the outcomes of the calculation significantly. To run this larger calculation, it must be sent to the HPC system.
The TlBr3 molecule was built on gaussian amd the calculation, using LANL2DZ basis set, was run through the HPC system. The resulting calculation output is accessible via this link to D-space: DOI:10042/22448
The Calculation Summary provided by Gaussian is shown in the table below:
| File name | TlBr3 optimisation output |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | LANL2DZ |
| E(RB3LYP) | -91.21812851 a.u. |
| RMS Gradient Norm | 0.00000090 a.u. |
| Dipole Moment | 0 (Debye) |
| Point Group | D3H |
| Job cpu time | 0 days 0 hours 0 minutes 28.6 seconds |
The "real" text based .log file allows us to check the convergence has been successful by checking the final set of forces and displacements shown below.
Item Value Threshold Converged?
Maximum Force 0.000002 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000022 0.001800 YES
RMS Displacement 0.000014 0.001200 YES
Predicted change in Energy=-6.084052D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 2.651 -DE/DX = 0.0 !
! R2 R(1,3) 2.651 -DE/DX = 0.0 !
! R3 R(1,4) 2.651 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The "YES" notations ins the "Converged?" colomn signify that convergence was achieved and the calculation was successful.
Therefore, the following data was recorded:
| Total Energy | -91.21812851 a.u. |
| T;-Br Bond Length | 120 degrees |
| Br-Tl_Br Bond Angle | 2.65095 Å |
The Tl-Br bond length was compared with literature value is 2,512 angstroms.[3] Therefore showing the calculated bond length to be within 0.15 angstroms of the calculated value.
Optimisation of BBr3 molecule using the HPC system
Similar to the TlBr3 case discussed above, the BBr3 molecule was built on Gaussian and the calculation, using basis set Gen, was sent to the HPC system.
The resulting calculation output was published in D-space and can be accessed by this link:DOI:10042/22463
The Summary provided by Gaussian is shown in the table below:
| File name | BBr3 Optimisation output |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | Gen |
| E(RB3LYP) | -64.43645296 a.u. |
| RMS Gradient Norm | 0.00000382 a.u. |
| Dipole Moment | 0 (Debye) |
| Point Group | D3H |
| Job cpu time | 0 days 0 hours 0 minutes 27.0 seconds |
The "real" text based .log file allows us to check the convergence has been successful by checking the final set of forces and displacements shown below.
Item Value Threshold Converged?
Maximum Force 0.000008 0.000450 YES
RMS Force 0.000005 0.000300 YES
Maximum Displacement 0.000036 0.001800 YES
RMS Displacement 0.000023 0.001200 YES
Predicted change in Energy=-4.027590D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.934 -DE/DX = 0.0 !
! R2 R(1,3) 1.934 -DE/DX = 0.0 !
! R3 R(1,4) 1.934 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Again, the "YES" notations in the "converged?" colomn signify that convergence has occurred and the calculation was successful.
| Total Energy | -64.43645296 a.u. |
| B-Br Bond Length | 1.93396 Å |
| Br-B-Br Bond Angle | 120 degrees |
A Literature value for the B-Br Bond length is 1.893254Å,[4]showing there to be ~0.1Å difference between the calculated and literature values.
Analysis and Comparison of Bond Lengths
The question, "what is a bond?" is a popular one. A bond is not a static, unyielding entity like the straight, solid line that generally depicts it. It is a versatile, concoction of electrons moving through overlapping orbitals that is always in contant motion.
| Molecule | BH3 | BBr3 | TlBr3 |
| Bond Length (Å) | 1.19189 | 1.93396 | 2.65095 |
In the table above are the calculated bond lengths from the optimisation of BH3, BBr3 and TlBr3 molecules. The molecules themselves differ from each other in terms of atomic size and differing ligands.
The change of ligand from H to Br causes an increase in bond length from 1.19189Å to 1.93396Å. Both ligand are X type, donating one electron into the bond with boron. However, H is a very small, highly charged, electropositive ligand with a 1s orbital that is of similar size to the lobe of the boron 2p orbital. Therefore, there is good overlap between these two orbitals and the hydrogen is held close to the Boron centre, giving it a short bond length. On the other hand, Br is a much larger atom, electronegative ligand in group 17 and period 4,with a more diffuse electron cloud. The bromine 4p orbital lobe does not overlap as well with the smaller with the smaller 2p boron orbital. Therefore the bromine is not held as tightly to the boron centre as Hydrogen making the bond significantly longer. Bromine's ability to pull the electrons in the bond to itself due to its electronegativity also substantially weakens the B-Br bond.
Comparing BBr3 and TlBr3 shows the effect of changing the central atom on the bond length. From the data in the table, it is possible to state that increasing the size of the central atom , subsequently increases the bond length between central atom and the ligand. Boron and Thallium are both in group 13 but Thallium inhabits period compared to Boron's period 2 making Thallium significantly larger. Bromine is equi-distant in terms of size therefore the molecules have similar degrees of overlap. Due to its size, Thallium's orbitals are much more diffuse and situated further away from the nucleus than boron making the 6p orbital less electropositive and able to attract the electronegative bromine. Boron's 2p orbital is situated much closer to the nucleus increasing the electrostatic attraction, thus causing the B-Br bond length to be significantly shorter than that of TlBr3.
Frequency Analysis
BH3 Molecule
Frequency Analysis was carried out in the same calculation as the optimisation of BH3 molecule using the 6-31G(d,p)Basis set as it provided more confirmation that the optimised structure has been obtained.
The calculation was done through gaussian and the link to the frequency calculation output is: Media: BH3_AT_631G.LOG.
The summary of the calculation provided by gaussian is tabulated below:
| File name | BH3_AT_631G |
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -26.61532363 a.u. |
| RMS Gradient Norm | 0.00000461 a.u. |
| Dipole Moment | 0 (Debye) |
| Point Group | D3H |
| Job cpu time | 0 days 0 hours 0 minutes 8.0 seconds |
Confirmation that the minimum potential energy structure has been reached is shown by the low frequencies below. They are all close to zero and within 15cm^-1 of each other.
Low frequencies --- -3.1264 -1.1139 -0.0053 1.5824 9.8979 9.9603 Low frequencies --- 1162.9837 1213.1741 1213.1768
Below is a table containing animations of the calculated vibrations.
| Number | Form of the Vibration | Description of Vibration | Frequency | Intensity | Symmetry |
| 1 |  |
All 3 hydrogens involved in symmetrical wag in and out of the plane | 1162.98 | 92.5495 | A"2 |
| 2 |  |
2 hydrogens involved in symmetrical scissoring motion whilst 1 Hydrogen remains static | 1213.17 | 14.0545 | E' |
| 3 |  |
All 3 hydrogens involved in an inplane rocking motion | 1213.18 | 14.0581 | E' |
| 4 |  |
All 3 hydrogens ivolved in symmetric stretching along the bonds | 2582.32 | 0.0000 | A'1 |
| 5 |  |
2 Hydrogens involved in asymnmetric stretch along the bond axis, 1 Hydrogen remains static | 2715.49 | 126.3286 | E' |
| 6 |  |
2 hydrogens involved in symmetric stretch along the bond axes which is asymmetric to the stretch along the bond axis of the 3rd hydrogen | 2715.50 | 126.3191 | E' |
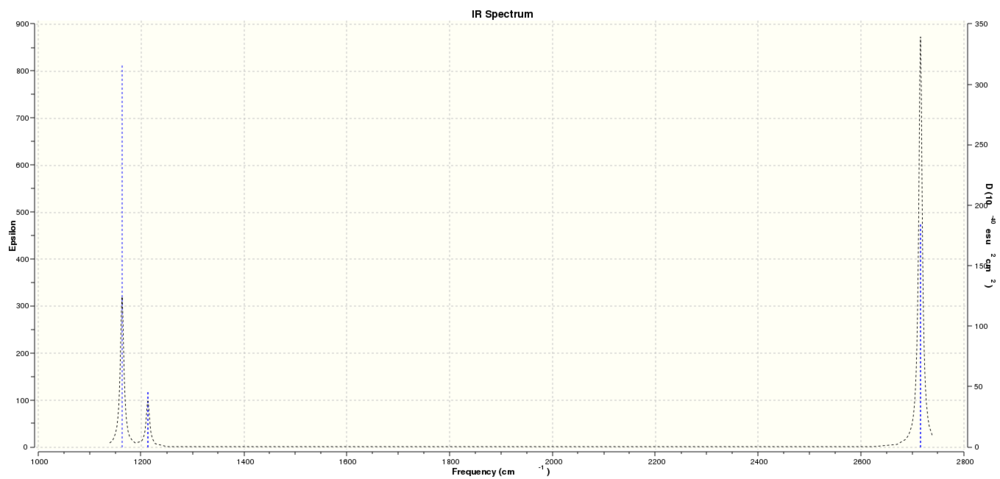
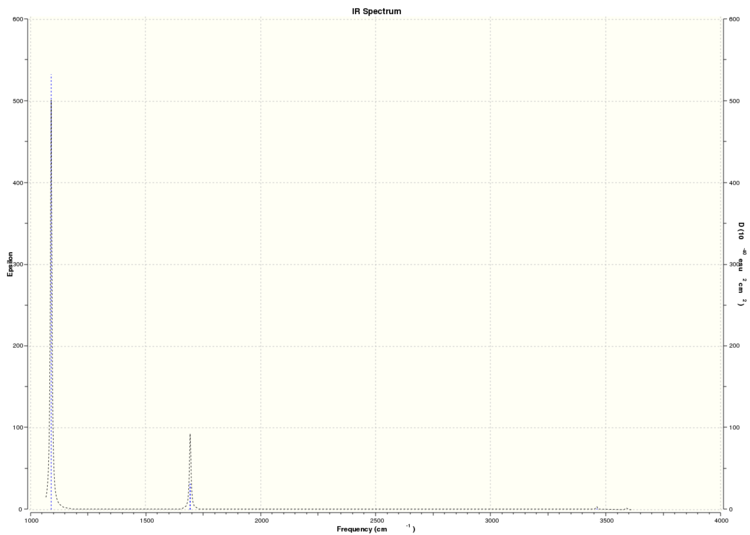
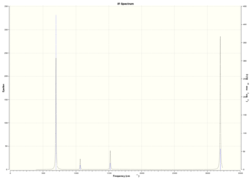
These vibrations correspond to the predicted IR spectrum for BH3 shown below:
Three peaks are visible for 6 vibrations because vibrations 2 and 3 have very similar frequencies at 1213.17cm^-1 and 1213.18cm^-1 which overlap and are therefore represented as one peak. The same happens with vibrations 5 and 6 at 2715.49cm^-1 and 2715.50cm^-1. Vibration 4 has zero intensity and therefore is not visible on the spectrum leading to only 3 peaks being visible.
TlBr3 Molecule
Frequency Analysis was carried out on the optimised TlBr3 using the LANL2DZ Basis set. The calculation was run through the HPC and the results published in D-space, accessible at this link: DOI:10042/22464
A summary of the calculation was tabulated below:
| File name | TlBr3 frequency output final |
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | LANL2DZ |
| E(RB3LYP) | -91.21812851 a.u. |
| RMS Gradient Norm | 0.00000088 a.u. |
| Dipole Moment | 0 (Debye) |
| Point Group | D3H |
| Job cpu time | 0 days 0 hours 0 minutes 36.6 seconds |
Confirmation that the minimum potential energy structure has been reached is shown by the low frequencies below. They are all close to zero and within 15cm^-1 of each other.
Low frequencies --- -3.4213 -0.0026 -0.0004 0.0015 3.9367 3.9367 Low frequencies --- 46.4289 46.4292 52.1449
Below is a table containing animations of the calculated vibrations.
| Number | Form of the Vibration | Description of Vibration | Frequency | Intensity | Symmetry |
| 1 |  |
2 hydrogens involved in symmetric scissoring, 1 hydrogen remains static | 46.43 | 3.6867 | E' |
| 2 |  |
All 3 hydrogens involved in a rocking motion | 46.63 | 3.6837 | E' |
| 3 |  |
3 hydrogens involved in out of plane wagging | 52.14 | 5.8466 | A2 |
| 4 |  |
All three hydrogens involved in symmetric stretching along bond axes | 165.27 | 0.0000 | A1' |
| 5 |  |
2 hydrogens involved in asymmetric stretching, one hydrogen remains static | 210.69 | 25.4830 | E' |
| 6 |  |
2 hydrogens involved in symmetric stretching whilst the other stretches asymmetrically to the other 2 | 210.69 | 25.4797 | E' |
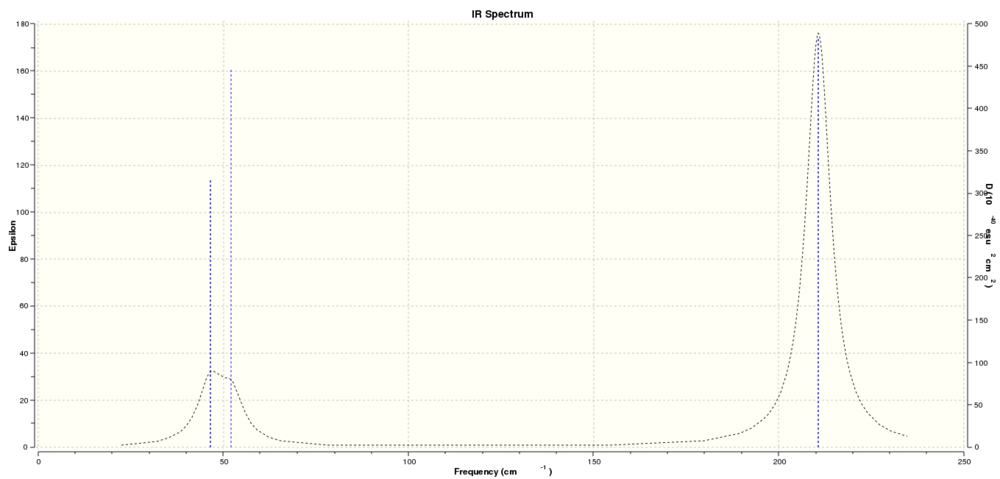
From these calculated the predicted IR spectrum for TlBr3 is shown below:
Again, as with BH3, for 6 vibrations only 3 peaks are visible. This is due to vibrations 1 and 2 having very similar frequencies at 46.43cm^-1 and 46.63cm^-1 and thus overlap on the spectrum. Vibrations 5 and 6 also overlap as both have frequency 210.69cm^-1. Vibration 4 has zero intensity and therefore does not feature on the IR spectrum. Thus leaving 3 peaks.
Population Analysis and Charge Distribution of BH3
A full NBO energy calculation was conducted using basis set 6-31G(d,p).
The calculation was run through the HPC system and the results were published in D-space, accessible by link DOI:10042/22538 .
A summary of the calculation is tabulated below:
| File name | checkpoint_BH3_MO4 |
| File Type | .fch |
| Calculation Type | SP |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(D,P) |
| E(RB3LYP) | -26.61532363 a.u. |
| RMS Gradient Norm | 0.00000000 a.u. |
| Dipole Moment | 0 (Debye) |
| Point Group | - |
| Job cpu time | - days - hours - minutes - seconds |
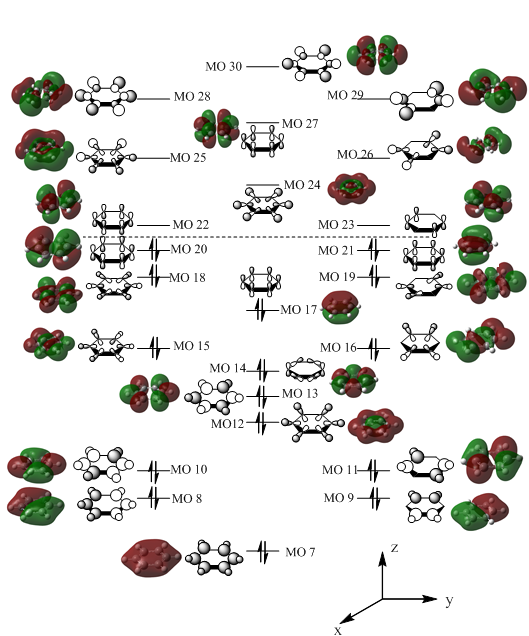
From the data collected from the calculation, it was possible to construct an MO diagram of the BH3. Shown below:
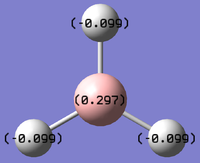
The charge distribution on BH3 is shown on the diagrams below:
The Boron molecule on the BH3 has a value of +0.297 showing it to be electropositive whilst the Hydrogen atoms have a charge of -0.099 showing them to be slightly electronegative. This suggests the Boron to be donating electrons to the hydrogen.
NH3 Molecule
Optimisation and Frequency Analysis of NH3
The calculation was carried out using the "opt+freq" method and the 6-31G (d,p) basis set, a higher basis set which was possible to use immediately due to the small size of the molecule, compared to the process used when optimising the BH3 molecule.
The resulting calculation .log file is linked here: Media:NH3_OPT_FREQ_CALC.LOG
The summary of the reaction is shown in the table below:
| File name | NH3_opt_freq_calc |
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -56.55776872 a.u. |
| RMS Gradient Norm | 0.00000878 a.u. |
| Dipole Moment | 1.8464 (Debye) |
| Point Group | C1 |
| Job cpu time | 0 days 0 hours 0 minutes 20.0 seconds |
The "real" text based .log file allows us to check the convergence has been successful by checking the final set of forces and displacements shown below.
Item Value Threshold Converged?
Maximum Force 0.000024 0.000450 YES
RMS Force 0.000012 0.000300 YES
Maximum Displacement 0.000079 0.001800 YES
RMS Displacement 0.000051 0.001200 YES
Predicted change in Energy=-1.624508D-09
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7406 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7479 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7479 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.862 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The "YES" answers in the "converge" colomn confirm that the data has converged and the calculation has been successful.
Therefore, this optimisation provides the following data:
| Final Energy | -56.55776872 a.u. |
| N-H Bond Length | 1.01800 Å |
| H-N-H Bond Angle | 105.748 degrees |
The calculated N-H Bond length value was compared with a literature value, 1.03–1.05 Å [5], and was found to be within ~ 0.05 Å. Frequency log file:
Confirmation that the minimum potential energy structure has been reached is shown by the low frequencies below. They are all close to zero and within 15cm^-1 of each other.
Low frequencies --- -6.7523 -0.0018 -0.0018 -0.0014 11.3367 16.0975 Low frequencies --- 1089.3546 1693.9209 1693.9586
Below is a table containing animations of the calculated vibrations:
| Number | Form of the Vibration | Description of Vibration | Frequency | Intensity |
| 1 |  |
symmetric wagging of 3H in and out of plane | 1089.35 | 145.4356 |
| 2 |  |
3 H in wagging motion | 1693.92 | 13.5601 |
| 3 |  |
2 H involved in scissoring motion, 1H static | 1693.96 | 13.5552 |
| 4 |  |
3 H symmetric stretching along the bond axes | 3461.23 | 1.0593 |
| 5 |  |
2H in symmetric stretching, 1H stretching asymmetrically to other 2H | 3589.73 | 0.2693 |
| 6 |  |
2H assymmetric stretching, 1H static | 3589.84 | 0.2703 |
These vibrations translate onto the predicted IR spectrum of NH3, shown below:
Only 2 peaks clearly visible, representing vibration 1 (at 1089.35 cm^-1) and vibrations 2 and 3 (at ~1693.94cm^-1. The other three vibrations are visible as two peaks but at very low intensity around 3500cm^-1.
Population Analysis of NH3
A NBO analysis of NH3 was conducted. The calculation was run through HPC system using basis set 6-31G(d,p)and job type "energy. The output was published in D-space:DOI::10042/22553 .
Summary of the calculation is tabulated below:
| File name | MO_NH3_final |
| File Type | .fch |
| Calculation Type | SP |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -56.55776856 a.u. |
| RMS Gradient Norm | 0.00000000 a.u. |
| Dipole Moment | 1.8465 (Debye) |
| Point Group | - |
| Job cpu time | - days - hours - minutes - seconds |
MO analysis shown below:
| MO | Gaussian MO | LCFAO | MO | Gaussian MO | LCFAO |
| 1 |  |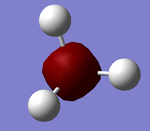
 |
5 (HOMO) |  |
|
| 2 |  |
 |
6 (LUMO) |  |
|
| 3 |  |
 |
7 |  |
|
| 4 |  |
 |
8 |  |
|
NBO Analysis of NH3
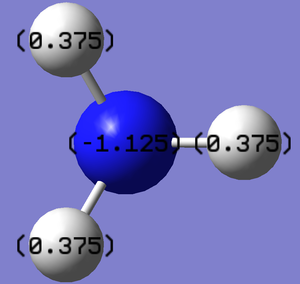
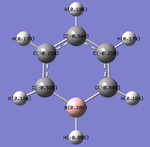
The charge distribution of NH3, displayed in the diagrams to the right, show a highly electronegative nitrogen with a value of -1.125 and electropositive hydrogens with values of 0.375. This distribution is due to the lone pair on the nitrogen as well as the ability of the nitrogen atom to pull electrons towards itself in the bond.
Hydrogen Storage: NH3BH3
Ammonia-borane, an acid-base complex, is being investigated for storage of hydrogen in the solid form, deemed to be much safer,due to its high hydrogen content and solid state stability at room temeperature.
The dative bond energy was calculated taking into account the previously calculated energies of BH3 and NH3 and that of NH3BH3.
Optimisation and Frequency Analysis of NH3BH3
The optimisation and frequency of the NH3BH3 molecule were calculated at the same time using the "opt+freq" job type and the 6-31G(d,p)basis. The calculations were run through the HPC system and the results published in D-space, accessible via this link: DOI::10042/22573 .
A summary of the calculation is tabulated below:
| File name | NH3BH3_Opt_freq_final_output |
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -83.22468905 a.u. |
| RMS Gradient Norm | 0.00000119 a.u. |
| Dipole Moment | 5.5647 (Debye) |
| Point Group | C1 |
| Job cpu time | 0 days 0 hours 2 minutes 3.2 seconds |
The "real" text based .log file allows us to check the convergence has been successful by checking the final set of forces and displacements shown below.
Item Value Threshold Converged?
Maximum Force 0.000002 0.000015 YES
RMS Force 0.000001 0.000010 YES
Maximum Displacement 0.000023 0.000060 YES
RMS Displacement 0.000009 0.000040 YES
Predicted change in Energy=-1.040362D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,7) 1.2098 -DE/DX = 0.0 !
! R2 R(2,7) 1.2098 -DE/DX = 0.0 !
! R3 R(3,7) 1.2098 -DE/DX = 0.0 !
! R4 R(4,8) 1.0185 -DE/DX = 0.0 !
! R5 R(5,8) 1.0185 -DE/DX = 0.0 !
! R6 R(6,8) 1.0185 -DE/DX = 0.0 !
! R7 R(7,8) 1.6677 -DE/DX = 0.0 !
! A1 A(1,7,2) 113.874 -DE/DX = 0.0 !
! A2 A(1,7,3) 113.874 -DE/DX = 0.0 !
! A3 A(1,7,8) 104.5972 -DE/DX = 0.0 !
! A4 A(2,7,3) 113.874 -DE/DX = 0.0 !
! A5 A(2,7,8) 104.5972 -DE/DX = 0.0 !
! A6 A(3,7,8) 104.5973 -DE/DX = 0.0 !
! A7 A(4,8,5) 107.8749 -DE/DX = 0.0 !
! A8 A(4,8,6) 107.8749 -DE/DX = 0.0 !
! A9 A(4,8,7) 111.0237 -DE/DX = 0.0 !
! A10 A(5,8,6) 107.8748 -DE/DX = 0.0 !
! A11 A(5,8,7) 111.0241 -DE/DX = 0.0 !
! A12 A(6,8,7) 111.0241 -DE/DX = 0.0 !
! D1 D(1,7,8,4) 180.0 -DE/DX = 0.0 !
! D2 D(1,7,8,5) -60.0 -DE/DX = 0.0 !
! D3 D(1,7,8,6) 60.0 -DE/DX = 0.0 !
! D4 D(2,7,8,4) -60.0 -DE/DX = 0.0 !
! D5 D(2,7,8,5) 60.0 -DE/DX = 0.0 !
! D6 D(2,7,8,6) 180.0 -DE/DX = 0.0 !
! D7 D(3,7,8,4) 60.0 -DE/DX = 0.0 !
! D8 D(3,7,8,5) 180.0 -DE/DX = 0.0 !
! D9 D(3,7,8,6) -60.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The "YES" answers in the "converge" colomn confirm that the data has converged and the calculation has been successful. Therefore, this optimisation provides the following data:
| Total Energy | -83.22468905 a.u. |
| B-N Bond Length | 1.66771 Å |
| B-H Bond Length | 1.20977 Å |
| N-H Bond Length | 1.01847 Å |
Therefore, the bonding between NH3 and BH3 causes a slight increase in the B-H bond length of 0.01788 Å and an even smaller increase in the N-H bond length of 0.00047 Å. This is due to the new bond causing the hydrogen atoms to be held less tightly. However, the difference is minimal.
Confirmation that the minimum potential energy structure has been reached is shown by the low frequencies below. They are all close to zero and within 15cm^-1 of each other.
Low frequencies --- -4.4618 -2.5163 -0.0011 -0.0011 -0.0005 1.3914 Low frequencies --- 263.4063 632.9621 638.4176
Analysis of vibrations is tabulated below:
Association Energy of NH3BH3
| E(BH3) | -26.61532335 a.u. |
| E(NH3) | -56.55776872 a.u |
| E(NH3BH3) | -83.22468905 a.u. |
ΔE = E(NH3BH3)- (E(BH3) + E(NH3))
ΔE = (-83.22468905) - (-26.61532335 +(-56.55776872))= -0.05159698 a.u.
ΔE = -0.05159698 a.u. = -135.47 kJ mol^-1
The calculated association energy of NH3BH3, shown above, is low and exothermic. This indicated weak, easily breakable bond. The bond itself is dative, with nitrogen donating a lone pair of electrons into the empty pz orbital on the boron. Therefore, the molecule displays lewis acid/base behaviour.
Investigation of Aromaticity
Benzene
Optimisation and Frequency Analysis of Benzene
A benzene molecule was built on Gaussian and a calculation was run using the method, "opt + freq", and basis set, 6-31G. The calculation was run through the HPC system.
The output was published on D-space and is accessible via the following link: DOI::10042/22575 .
The summary of the calculation is tabulated below:
| File name | benzene_opt_freq_calc_631G_output |
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -232.25820415 a.u. |
| RMS Gradient Norm | 0.00000849 a.u. |
| Dipole Moment | 0 (Debye) |
| Point Group | C1 |
| Job cpu time | 0 days 0 hours 10 minutes 38.5 seconds |
The "real" text based .log file allows us to check the convergence has been successful by checking the final set of forces and displacements shown below.
Item Value Threshold Converged?
Maximum Force 0.000013 0.000015 YES
RMS Force 0.000004 0.000010 YES
Maximum Displacement 0.000052 0.000060 YES
RMS Displacement 0.000017 0.000040 YES
Predicted change in Energy=-1.961187D-09
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.3964 -DE/DX = 0.0 !
! R2 R(1,6) 1.3963 -DE/DX = 0.0 !
! R3 R(1,7) 1.0863 -DE/DX = 0.0 !
! R4 R(2,3) 1.3963 -DE/DX = 0.0 !
! R5 R(2,8) 1.0863 -DE/DX = 0.0 !
! R6 R(3,4) 1.3964 -DE/DX = 0.0 !
! R7 R(3,9) 1.0863 -DE/DX = 0.0 !
! R8 R(4,5) 1.3963 -DE/DX = 0.0 !
! R9 R(4,10) 1.0863 -DE/DX = 0.0 !
! R10 R(5,6) 1.3964 -DE/DX = 0.0 !
! R11 R(5,11) 1.0863 -DE/DX = 0.0 !
! R12 R(6,12) 1.0863 -DE/DX = 0.0 !
! A1 A(2,1,6) 119.9999 -DE/DX = 0.0 !
! A2 A(2,1,7) 119.9988 -DE/DX = 0.0 !
! A3 A(6,1,7) 120.0013 -DE/DX = 0.0 !
! A4 A(1,2,3) 120.0001 -DE/DX = 0.0 !
! A5 A(1,2,8) 119.9977 -DE/DX = 0.0 !
! A6 A(3,2,8) 120.0022 -DE/DX = 0.0 !
! A7 A(2,3,4) 120.0 -DE/DX = 0.0 !
! A8 A(2,3,9) 120.0015 -DE/DX = 0.0 !
! A9 A(4,3,9) 119.9985 -DE/DX = 0.0 !
! A10 A(3,4,5) 119.9999 -DE/DX = 0.0 !
! A11 A(3,4,10) 119.9978 -DE/DX = 0.0 !
! A12 A(5,4,10) 120.0023 -DE/DX = 0.0 !
! A13 A(4,5,6) 120.0001 -DE/DX = 0.0 !
! A14 A(4,5,11) 120.0012 -DE/DX = 0.0 !
! A15 A(6,5,11) 119.9987 -DE/DX = 0.0 !
! A16 A(1,6,5) 120.0 -DE/DX = 0.0 !
! A17 A(1,6,12) 120.002 -DE/DX = 0.0 !
! A18 A(5,6,12) 119.998 -DE/DX = 0.0 !
! D1 D(6,1,2,3) -0.0003 -DE/DX = 0.0 !
! D2 D(6,1,2,8) 180.0 -DE/DX = 0.0 !
! D3 D(7,1,2,3) 179.9997 -DE/DX = 0.0 !
! D4 D(7,1,2,8) 0.0 -DE/DX = 0.0 !
! D5 D(2,1,6,5) -0.0002 -DE/DX = 0.0 !
! D6 D(2,1,6,12) 180.0001 -DE/DX = 0.0 !
! D7 D(7,1,6,5) 179.9998 -DE/DX = 0.0 !
! D8 D(7,1,6,12) 0.0001 -DE/DX = 0.0 !
! D9 D(1,2,3,4) 0.0006 -DE/DX = 0.0 !
! D10 D(1,2,3,9) 180.0002 -DE/DX = 0.0 !
! D11 D(8,2,3,4) 180.0002 -DE/DX = 0.0 !
! D12 D(8,2,3,9) -0.0002 -DE/DX = 0.0 !
! D13 D(2,3,4,5) -0.0003 -DE/DX = 0.0 !
! D14 D(2,3,4,10) 179.9997 -DE/DX = 0.0 !
! D15 D(9,3,4,5) -180.0 -DE/DX = 0.0 !
! D16 D(9,3,4,10) 0.0001 -DE/DX = 0.0 !
! D17 D(3,4,5,6) -0.0002 -DE/DX = 0.0 !
! D18 D(3,4,5,11) 180.0002 -DE/DX = 0.0 !
! D19 D(10,4,5,6) 179.9998 -DE/DX = 0.0 !
! D20 D(10,4,5,11) 0.0001 -DE/DX = 0.0 !
! D21 D(4,5,6,1) 0.0004 -DE/DX = 0.0 !
! D22 D(4,5,6,12) 180.0002 -DE/DX = 0.0 !
! D23 D(11,5,6,1) 180.0001 -DE/DX = 0.0 !
! D24 D(11,5,6,12) -0.0002 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The "YES" answers in the "converge" colomn confirm that the data has converged and the calculation has been successful. Therefore, this optimisation provides the following data:
| Final Energy | -232.25820415 a.u. |
| C-C Bond length | 1.39636 Å |
| C-H Bond Length | 1.08635 Å |
All the C-C bonds are equal signifying delocalisation of electrons around the ring.
Confirmation that the minimum potential energy structure has been reached is shown by the low frequencies below. They are all close to zero and within 15cm^-1 of each other.
Low frequencies --- -4.7115 -0.0009 -0.0007 -0.0006 5.2723 6.2068 Low frequencies --- 414.5308 414.5721 621.0881
There for this calculation provide information about the numerous, 30 in total, vibrational modes of the benzene ring. Tabulated below:
| Vibration mode | Frequency | Infrared | Vibration mode | Frequency | Infrared |
| 1 | 414.53 | 0.0000 | 16 | 1179.64 | 0.0000 |
| 2 | 414.57 | 0.0000 | 17 | 1202.50 | 0.0000 |
| 3 | 621.09 | 0.0000 | 18 | 1202.52 | 0.0000 |
| 4 | 621.09 | 0.0000 | 19 | 1355.52 | 0.0000 |
| 5 | 694.74 | 74.2411 | 20 | 1380.69 | 0.0000 |
| 6 | 718.39 | 0.0000 | 21 | 1524.45 | 6.6239 |
| 7 | 865.29 | 0.0000 | 22 | 1524.46 | 6.6293 |
| 8 | 865.34 | 0.0000 | 23 | 1652.66 | 0.0000 |
| 9 | 974.59 | 0.0000 | 24 | 1652.69 | 0.0000 |
| 10 | 974.62 | 0.0000 | 25 | 3171.71 | 0.0001 |
| 11 | 1013.25 | 0.0000 | 26 | 3181.26 | 0.0000 |
| 12 | 1017.80 | 0.0000 | 27 | 3181.30 | 0.0000 |
| 13 | 1019.52 | 0.0000 | 28 | 3196.93 | 46.6234 |
| 14 | 1066.46 | 0.0000 | 29 | 3196.97 | 46.6128 |
| 15 | 1066.47 | 3.3811 | 30 | 3207.54 | 0.0000 |
These vibrations are used to predict the IR spectrum of benzene, shown to the right of this page. There are not 30 peaks visible on the spectrum as many molecules have minimal or no intensity and thus do not show up. Others, that do have significant intensity, have very similar frequencies and thus overlap, showing up as a single peak.
Population Distribution Analysis of Benzene
The calculation was run through the HPC system using the optimised Benzene molecule from the previous calculation. The calculation used the "Energy" method and the 6-31G Basis set. The output of the calculation was published on D-space which is accessible via this link: DOI::10042/ .
A summary of the calculation is tabulated below:
| File name | Benzene_MO_output |
| File Type | .fch |
| Calculation Type | SP |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -232.25820674 a.u. |
| RMS Gradient Norm | 0.00000000 a.u. |
| Dipole Moment | 0 (Debye) |
| Point Group | - |
| Job cpu time | - days - hours - minutes - seconds |
MO Analysis
Using the calculated MOs, an MO diagram of benzene was built focusing on both sigma and pi interations:
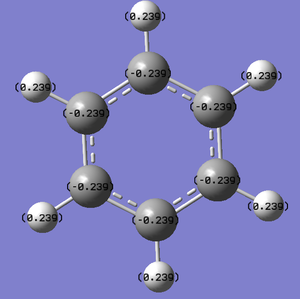
Charge Distribution of Benzene
The charge distribution of benzene is illustrated to the right of this page. It shows negative charge evenly distributed over the carbons situated in the ring with a value of -0.084, whilst the hydrogens have a positive charge of 0.084 as their single electron has been donated into the C-H bond.
Boratabenzene
Optimisation and Frequency Analysis of Boratabenzene
A boratabenzene molecule was built on Gaussian and a calculation was run using the method, "opt + freq", and basis set, 6-31G. The calculation was run through the HPC system.
The output was published on D-space and is accessible via the following link: DOI::10042/22639 .
The summary of the calculation is tabulated below:
| File name | Boratabenzene_opt_freq_output |
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | -1 |
| Spin | Singlet |
| E(RB3LYP) | -219.02052299a.u. |
| RMS Gradient Norm | 0.00000174a.u. |
| Dipole Moment | 2.8455(Debye) |
| Point Group | C1 |
| Job cpu time | 0 days 0 hours 10 minutes 35.8 seconds |
The "real" text based .log file allows us to check the convergence has been successful by checking the final set of forces and displacements shown below.
Item Value Threshold Converged?
Maximum Force 0.000004 0.000015 YES
RMS Force 0.000001 0.000010 YES
Maximum Displacement 0.000019 0.000060 YES
RMS Displacement 0.000005 0.000040 YES
Predicted change in Energy=-1.109824D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.3988 -DE/DX = 0.0 !
! R2 R(1,6) 1.0968 -DE/DX = 0.0 !
! R3 R(1,12) 1.5141 -DE/DX = 0.0 !
! R4 R(2,3) 1.4051 -DE/DX = 0.0 !
! R5 R(2,7) 1.0969 -DE/DX = 0.0 !
! R6 R(3,4) 1.4052 -DE/DX = 0.0 !
! R7 R(3,8) 1.0915 -DE/DX = 0.0 !
! R8 R(4,5) 1.3988 -DE/DX = 0.0 !
! R9 R(4,9) 1.0969 -DE/DX = 0.0 !
! R10 R(5,10) 1.0968 -DE/DX = 0.0 !
! R11 R(5,12) 1.5141 -DE/DX = 0.0 !
! R12 R(11,12) 1.2185 -DE/DX = 0.0 !
! A1 A(2,1,6) 116.0115 -DE/DX = 0.0 !
! A2 A(2,1,12) 120.0604 -DE/DX = 0.0 !
! A3 A(6,1,12) 123.928 -DE/DX = 0.0 !
! A4 A(1,2,3) 122.1801 -DE/DX = 0.0 !
! A5 A(1,2,7) 120.3636 -DE/DX = 0.0 !
! A6 A(3,2,7) 117.4563 -DE/DX = 0.0 !
! A7 A(2,3,4) 120.4148 -DE/DX = 0.0 !
! A8 A(2,3,8) 119.7927 -DE/DX = 0.0 !
! A9 A(4,3,8) 119.7925 -DE/DX = 0.0 !
! A10 A(3,4,5) 122.18 -DE/DX = 0.0 !
! A11 A(3,4,9) 117.4562 -DE/DX = 0.0 !
! A12 A(5,4,9) 120.3639 -DE/DX = 0.0 !
! A13 A(4,5,10) 116.0119 -DE/DX = 0.0 !
! A14 A(4,5,12) 120.0605 -DE/DX = 0.0 !
! A15 A(10,5,12) 123.9276 -DE/DX = 0.0 !
! A16 A(1,12,5) 115.1042 -DE/DX = 0.0 !
! A17 A(1,12,11) 122.4483 -DE/DX = 0.0 !
! A18 A(5,12,11) 122.4475 -DE/DX = 0.0 !
! D1 D(6,1,2,3) 179.9996 -DE/DX = 0.0 !
! D2 D(6,1,2,7) 0.0 -DE/DX = 0.0 !
! D3 D(12,1,2,3) -0.0003 -DE/DX = 0.0 !
! D4 D(12,1,2,7) 180.0002 -DE/DX = 0.0 !
! D5 D(2,1,12,5) 0.0 -DE/DX = 0.0 !
! D6 D(2,1,12,11) -180.0 -DE/DX = 0.0 !
! D7 D(6,1,12,5) 180.0001 -DE/DX = 0.0 !
! D8 D(6,1,12,11) 0.0001 -DE/DX = 0.0 !
! D9 D(1,2,3,4) 0.0006 -DE/DX = 0.0 !
! D10 D(1,2,3,8) 180.0004 -DE/DX = 0.0 !
! D11 D(7,2,3,4) 180.0002 -DE/DX = 0.0 !
! D12 D(7,2,3,8) -0.0001 -DE/DX = 0.0 !
! D13 D(2,3,4,5) -0.0006 -DE/DX = 0.0 !
! D14 D(2,3,4,9) -180.0001 -DE/DX = 0.0 !
! D15 D(8,3,4,5) -180.0004 -DE/DX = 0.0 !
! D16 D(8,3,4,9) 0.0001 -DE/DX = 0.0 !
! D17 D(3,4,5,10) 180.0004 -DE/DX = 0.0 !
! D18 D(3,4,5,12) 0.0003 -DE/DX = 0.0 !
! D19 D(9,4,5,10) -0.0001 -DE/DX = 0.0 !
! D20 D(9,4,5,12) 179.9998 -DE/DX = 0.0 !
! D21 D(4,5,12,1) 0.0 -DE/DX = 0.0 !
! D22 D(4,5,12,11) 180.0 -DE/DX = 0.0 !
! D23 D(10,5,12,1) 179.9999 -DE/DX = 0.0 !
! D24 D(10,5,12,11) -0.0001 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The "YES" answers in the "converge" colomn confirm that the data has converged and the calculation has been successful. Therefore, this optimisation provides the following data:
| Final Energy | -219.02052299 a.u. |
| B-C Bond length | 1.15408 Å |
| C1-C2/C4-C5 Bond Length | 1.39883 Å |
| C2-C3/C3-C4 Bond Length | 1.40515 Å |
| B-H Bond Length | 1.21846 Å |
| C-H Bond Length | 1.09682 Å |
Confirmation that the minimum potential energy structure has been reached is shown by the low frequencies below. They are all close to zero and within 15cm^-1 of each other.
Low frequencies --- -7.1681 -0.0005 0.0006 0.0007 3.3368 4.7083 Low frequencies --- 371.3001 404.4172 565.0798
| Vibration mode | Frequency | Infrared | Vibration mode | Frequency | Infrared |
| 1 | 371.30 | 2.3049 | 16 | 1084.78 | 3.3531 |
| 2 | 404.42 | 0.0000 | 17 | 1175.12 | 0.9440 |
| 3 | 565.08 | 0.1557 | 18 | 1179.84 | 1.0096 |
| 4 | 568.34 | 0.0886 | 19 | 1227.44 | 1.3489 |
| 5 | 607.65 | 11.4062 | 20 | 1333.45 | 30.6983 |
| 6 | 710.69 | 3.3451 | 21 | 1449.00 | 9.1261 |
| 7 | 755.89 | 7.1901 | 22 | 1462.98 | 13.8634 |
| 8 | 814.69 | 0.0000 | 23 | 1564.60 | 7.2353 |
| 9 | 873.45 | 27.8569 | 24 | 1591.91 | 40.2292 |
| 10 | 905.92 | 0.1173 | 25 | 2446.79 | 368.3131 |
| 11 | 917.18 | 0.8672 | 26 | 3027.46 | 108.1318 |
| 12 | 950.73 | 0.3362 | 27 | 3029.66 | 0.1235 |
| 13 | 951.37 | 0.0000 | 28 | 3059.75 | 379.6621 |
| 14 | 960.39 | 1.8173 | 29 | 3061.34 | 10.0794 |
| 15 | 1012.27 | 3.9348 | 30 | 3116.23 | 111.9970 |
From this vibrational data, the IR spectrum for boratabenzene has been predicted. It can be seen to the right of this page.
Population distribution of Boratabenzene
The calculation was run through the HPC system using the optimised Boratabenzene molecule from the previous calculation. The calculation used the "Energy" method and the 6-31G Basis set.
The output of the calculation was published on D-space which is accessible via this link: DOI::10042/22650 .
A summary of the calculation is tabulated below:
| File name | checkpoint_boratabenzene_MO_output |
| File Type | .fch |
| Calculation Type | SP |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -219.02053056 a.u. |
| RMS Gradient Norm | 0.00000000 a.u. |
| Dipole Moment | 2.8454 (Debye) |
| Point Group | - |
| Job cpu time | - days - hours - minutes - seconds |
MO analysis
The calculated HOMO and LUMO MOs are pictured below: ple.jp
| MO | 7 | 20 (HOMO) | 21 (LUMO) |
| Gaussian depiction |  |
.png) |
.png)
|
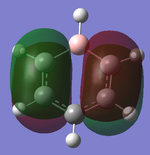| Energy (a.u.) | -0.60437 | -0.03492 | 0.01095 |
Charge Distribution Analysis
Pyridinium
Optimisation and Frequency Analysis of Pyridinium
A Pyridinium molecule was built on Gaussian and a calculation was run using the method, "opt + freq", and basis set, 6-31G. The calculation was run through the HPC system.
The output was published on D-space and is accessible via the following link: DOI::10042/22648 .
The summary of the calculation is tabulated below:
| File name | Pyridinium_opt_freq_output |
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 1 |
| Spin | Singlet |
| E(RB3LYP) | -248.66806092 a.u. |
| RMS Gradient Norm | 0.00000206 a.u. |
| Dipole Moment | 1.8723(Debye) |
| Point Group | C1 |
| Job cpu time | 0 days 0 hours 10 minutes 44.1 seconds |
The "real" text based .log file allows us to check the convergence has been successful by checking the final set of forces and displacements shown below.
Item Value Threshold Converged?
Maximum Force 0.000004 0.000015 YES
RMS Force 0.000001 0.000010 YES
Maximum Displacement 0.000009 0.000060 YES
RMS Displacement 0.000003 0.000040 YES
Predicted change in Energy=-9.673373D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.3838 -DE/DX = 0.0 !
! R2 R(1,6) 1.0832 -DE/DX = 0.0 !
! R3 R(1,12) 1.3524 -DE/DX = 0.0 !
! R4 R(2,3) 1.3987 -DE/DX = 0.0 !
! R5 R(2,7) 1.0835 -DE/DX = 0.0 !
! R6 R(3,4) 1.3987 -DE/DX = 0.0 !
! R7 R(3,8) 1.0852 -DE/DX = 0.0 !
! R8 R(4,5) 1.3838 -DE/DX = 0.0 !
! R9 R(4,9) 1.0835 -DE/DX = 0.0 !
! R10 R(5,10) 1.0832 -DE/DX = 0.0 !
! R11 R(5,12) 1.3524 -DE/DX = 0.0 !
! R12 R(11,12) 1.0169 -DE/DX = 0.0 !
! A1 A(2,1,6) 123.9409 -DE/DX = 0.0 !
! A2 A(2,1,12) 119.2365 -DE/DX = 0.0 !
! A3 A(6,1,12) 116.8226 -DE/DX = 0.0 !
! A4 A(1,2,3) 119.0801 -DE/DX = 0.0 !
! A5 A(1,2,7) 119.4448 -DE/DX = 0.0 !
! A6 A(3,2,7) 121.475 -DE/DX = 0.0 !
! A7 A(2,3,4) 120.0618 -DE/DX = 0.0 !
! A8 A(2,3,8) 119.9693 -DE/DX = 0.0 !
! A9 A(4,3,8) 119.9689 -DE/DX = 0.0 !
! A10 A(3,4,5) 119.0802 -DE/DX = 0.0 !
! A11 A(3,4,9) 121.4746 -DE/DX = 0.0 !
! A12 A(5,4,9) 119.4452 -DE/DX = 0.0 !
! A13 A(4,5,10) 123.9413 -DE/DX = 0.0 !
! A14 A(4,5,12) 119.2364 -DE/DX = 0.0 !
! A15 A(10,5,12) 116.8223 -DE/DX = 0.0 !
! A16 A(1,12,5) 123.305 -DE/DX = 0.0 !
! A17 A(1,12,11) 118.3476 -DE/DX = 0.0 !
! A18 A(5,12,11) 118.3474 -DE/DX = 0.0 !
! D1 D(6,1,2,3) 180.0001 -DE/DX = 0.0 !
! D2 D(6,1,2,7) 0.0 -DE/DX = 0.0 !
! D3 D(12,1,2,3) -0.0001 -DE/DX = 0.0 !
! D4 D(12,1,2,7) 179.9998 -DE/DX = 0.0 !
! D5 D(2,1,12,5) 0.0004 -DE/DX = 0.0 !
! D6 D(2,1,12,11) 180.0002 -DE/DX = 0.0 !
! D7 D(6,1,12,5) -179.9997 -DE/DX = 0.0 !
! D8 D(6,1,12,11) 0.0 -DE/DX = 0.0 !
! D9 D(1,2,3,4) -0.0001 -DE/DX = 0.0 !
! D10 D(1,2,3,8) 180.0 -DE/DX = 0.0 !
! D11 D(7,2,3,4) 180.0 -DE/DX = 0.0 !
! D12 D(7,2,3,8) 0.0001 -DE/DX = 0.0 !
! D13 D(2,3,4,5) -0.0001 -DE/DX = 0.0 !
! D14 D(2,3,4,9) -180.0001 -DE/DX = 0.0 !
! D15 D(8,3,4,5) 179.9998 -DE/DX = 0.0 !
! D16 D(8,3,4,9) -0.0001 -DE/DX = 0.0 !
! D17 D(3,4,5,10) 179.9999 -DE/DX = 0.0 !
! D18 D(3,4,5,12) 0.0005 -DE/DX = 0.0 !
! D19 D(9,4,5,10) -0.0002 -DE/DX = 0.0 !
! D20 D(9,4,5,12) -179.9996 -DE/DX = 0.0 !
! D21 D(4,5,12,1) -0.0006 -DE/DX = 0.0 !
! D22 D(4,5,12,11) 179.9996 -DE/DX = 0.0 !
! D23 D(10,5,12,1) 179.9999 -DE/DX = 0.0 !
! D24 D(10,5,12,11) 0.0002 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The "YES" answers in the "converge" colomn confirm that the data has converged and the calculation has been successful. Therefore, this optimisation provides the following data:
| Final Energy | -248.66806092 a.u. |
| N-C Bond length | 1.35242 Å |
| C1-C2/C4-C5 Bond Length | 1.38384 Å |
| C2-C3/C3-C4 Bond Length | 1.39873 Å |
| C-H Bond Length | 1.08324 Å |
| N-H Bond Length | 1.01688 Å |
Confirmation that the minimum potential energy structure has been reached is shown by the low frequencies below. They are all close to zero and within 15cm^-1 of each other.
Low frequencies --- -9.3858 -2.9630 -0.0010 -0.0007 0.0007 0.8916 Low frequencies --- 391.9002 404.3427 620.1995
The Vibrational data is tabulated below:
| Vibration mode | Frequency | Infrared | Vibration mode | Frequency | Infrared |
| 1 | 391.90 | 0.9882 | 16 | 1199.74 | 2.7165 |
| 2 | 404.34 | 0.0000 | 17 | 1228.72 | 1.7791 |
| 3 | 620.20 | 0.0146 | 18 | 1299.79 | 3.1809 |
| 4 | 645.16 | 0.2822 | 19 | 1374.07 | 10.6717 |
| 5 | 676.74 | 89.6612 | 20 | 1416.09 | 3.0787 |
| 6 | 747.69 | 82.3452 | 21 | 1523.67 | 21.0681 |
| 7 | 854.07 | 10.7751 | 22 | 1580.24 | 47.8967 |
| 8 | 882.78 | 0.0000 | 23 | 1656.63 | 31.8271 |
| 9 | 991.90 | 1.5297 | 24 | 1676.54 | 33.7930 |
| 10 | 1005.67 | 0.0000 | 25 | 3223.31 | 0.3000 |
| 11 | 1022.44 | 3.6548 | 26 | 3240.17 | 0.9864 |
| 12 | 1047.81 | 0.4354 | 27 | 3241.69 | 10.8548 |
| 13 | 1052.26 | 0.4123 | 28 | 3252.43 | 20.2777 |
| 14 | 2.7165 | 29 | 3253.79 | 0.3936 | |
| 15 | 1087.16 | 4.2176 | 30 | 3569.78 | 158.4642 |
From this data it was possible to predict the IR spectrum of Pyridinium, which can be viewed to the right of the page.
Population Distribution of Pyridinium
The calculation was run through the HPC system using the optimised Pyridinium molecule from the previous calculation. The calculation used the "Energy" method and the 6-31G Basis set.
The output of the calculation was published on D-space which is accessible via this link: DOI::10042/22651 .
A summary of the calculation is tabulated below:
| File name | checkpoint_pyridinium_MO_output |
| File Type | .fch |
| Calculation Type | SP |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 1 |
| Spin | Singlet |
| E(RB3LYP) | -248.66807403 a.u. |
| RMS Gradient Norm | 0.00000000 a.u. |
| Dipole Moment | 1.8723 (Debye) |
| Point Group | - |
| Job cpu time | - days - hours - minutes - seconds |
MO Analysis of Pyridinium
The calculated HOMO and LUMO MOs are pictured below: ple.jp
| MO | 7 | 20 (HOMO) | 21 (LUMO) |
| Gaussian depiction |  |
_pyr.png) |
_pyr.png)
|
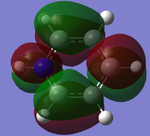
| Energy (a.u.) | -1.21399 | -0.47886 | -0.25841 |
Electronegative nitrogen pulls the electron cloud towards itself, depicted in MO7. This is backed up by the charge distribution values in the next section.
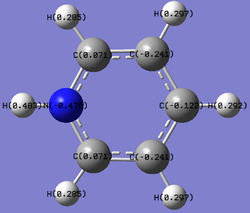
Charge Distribution of Pyridinium
The illustration to the right displays the trend charge distribution over the pyridinium molecule. The nitrogen atom possesses a high negative charge of -0.476 due to its electronegativity and ability to pull electrons towards itself. Therefore as it pulls electrons towards itself from the delocalised electron cloud, the adjacent carbons become more positive the further away from nitrogen they are situated. The same trend appears with the hydrogen, but to a lesser degree.
Borazine
Optimisation and Frequency Analysis of Borazine
A Borazine molecule was built on Gaussian and a calculation was run using the method, "opt + freq", and basis set, 6-31G. The calculation was run through the HPC system.
The output was published on D-space and is accessible via the following link: DOI::10042/22654 .
The summary of the calculation is tabulated below:
| File name | borazine_opt_freq_output |
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -242.68459923 a.u. |
| RMS Gradient Norm | 0.00000252 a.u. |
| Dipole Moment | 0(Debye) |
| Point Group | C1 |
| Job cpu time | 0 days 0 hours 10 minutes 38.3 seconds |
The "real" text based .log file allows us to check the convergence has been successful by checking the final set of forces and displacements shown below.
Item Value Threshold Converged?
Maximum Force 0.000005 0.000015 YES
RMS Force 0.000002 0.000010 YES
Maximum Displacement 0.000033 0.000060 YES
RMS Displacement 0.000012 0.000040 YES
Predicted change in Energy=-3.539488D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,7) 1.1951 -DE/DX = 0.0 !
! R2 R(2,10) 1.0097 -DE/DX = 0.0 !
! R3 R(3,9) 1.1951 -DE/DX = 0.0 !
! R4 R(4,11) 1.0097 -DE/DX = 0.0 !
! R5 R(5,8) 1.1951 -DE/DX = 0.0 !
! R6 R(6,12) 1.0097 -DE/DX = 0.0 !
! R7 R(7,10) 1.4306 -DE/DX = 0.0 !
! R8 R(7,12) 1.4306 -DE/DX = 0.0 !
! R9 R(8,11) 1.4306 -DE/DX = 0.0 !
! R10 R(8,12) 1.4306 -DE/DX = 0.0 !
! R11 R(9,10) 1.4306 -DE/DX = 0.0 !
! R12 R(9,11) 1.4306 -DE/DX = 0.0 !
! A1 A(1,7,10) 121.4338 -DE/DX = 0.0 !
! A2 A(1,7,12) 121.4349 -DE/DX = 0.0 !
! A3 A(10,7,12) 117.1314 -DE/DX = 0.0 !
! A4 A(5,8,11) 121.4346 -DE/DX = 0.0 !
! A5 A(5,8,12) 121.4345 -DE/DX = 0.0 !
! A6 A(11,8,12) 117.1309 -DE/DX = 0.0 !
! A7 A(3,9,10) 121.4341 -DE/DX = 0.0 !
! A8 A(3,9,11) 121.4335 -DE/DX = 0.0 !
! A9 A(10,9,11) 117.1324 -DE/DX = 0.0 !
! A10 A(2,10,7) 118.5656 -DE/DX = 0.0 !
! A11 A(2,10,9) 118.5667 -DE/DX = 0.0 !
! A12 A(7,10,9) 122.8677 -DE/DX = 0.0 !
! A13 A(4,11,8) 118.5665 -DE/DX = 0.0 !
! A14 A(4,11,9) 118.565 -DE/DX = 0.0 !
! A15 A(8,11,9) 122.8684 -DE/DX = 0.0 !
! A16 A(6,12,7) 118.5654 -DE/DX = 0.0 !
! A17 A(6,12,8) 118.5655 -DE/DX = 0.0 !
! A18 A(7,12,8) 122.8692 -DE/DX = 0.0 !
! D1 D(1,7,10,2) -0.001 -DE/DX = 0.0 !
! D2 D(1,7,10,9) 180.001 -DE/DX = 0.0 !
! D3 D(12,7,10,2) 179.999 -DE/DX = 0.0 !
! D4 D(12,7,10,9) 0.001 -DE/DX = 0.0 !
! D5 D(1,7,12,6) -0.0005 -DE/DX = 0.0 !
! D6 D(1,7,12,8) -179.9999 -DE/DX = 0.0 !
! D7 D(10,7,12,6) 179.9995 -DE/DX = 0.0 !
! D8 D(10,7,12,8) 0.0001 -DE/DX = 0.0 !
! D9 D(5,8,11,4) 0.0007 -DE/DX = 0.0 !
! D10 D(5,8,11,9) 179.9999 -DE/DX = 0.0 !
! D11 D(12,8,11,4) 180.0007 -DE/DX = 0.0 !
! D12 D(12,8,11,9) 0.0 -DE/DX = 0.0 !
! D13 D(5,8,12,6) 0.0001 -DE/DX = 0.0 !
! D14 D(5,8,12,7) 179.9996 -DE/DX = 0.0 !
! D15 D(11,8,12,6) -179.9999 -DE/DX = 0.0 !
! D16 D(11,8,12,7) -0.0005 -DE/DX = 0.0 !
! D17 D(3,9,10,2) 0.0005 -DE/DX = 0.0 !
! D18 D(3,9,10,7) 179.9986 -DE/DX = 0.0 !
! D19 D(11,9,10,2) 180.0005 -DE/DX = 0.0 !
! D20 D(11,9,10,7) -0.0015 -DE/DX = 0.0 !
! D21 D(3,9,11,4) 0.0002 -DE/DX = 0.0 !
! D22 D(3,9,11,8) 180.0009 -DE/DX = 0.0 !
! D23 D(10,9,11,4) 180.0002 -DE/DX = 0.0 !
! D24 D(10,9,11,8) 0.001 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The "YES" answers in the "converge" colomn confirm that the data has converged and the calculation has been successful. Therefore, this optimisation provides the following data:
| Final Energy | -242.68459923 a.u. |
| N-B Bond length | 1.43057 Å |
| N-H Bond Length | 1.00971 Å |
| B-H Bond Length | 1.19513 Å |
Confirmation that the minimum potential energy structure has been reached is shown by the low frequencies below. They are all close to zero and within 15cm^-1 of each other.
Low frequencies --- -7.7519 -0.0012 -0.0008 -0.0006 2.4711 6.8240 Low frequencies --- 289.5806 289.6796 404.4482
The vibrational information gained by this calculation is tabulated below.
| Vibration mode | Frequency | Infrared | Vibration mode | Frequency | Infrared |
| 1 | 289.58 | 0.0000 | 16 | 1052.11 | 0.0000 |
| 2 | 289.68 | 0.0000 | 17 | 1080.78 | 0.2052 |
| 3 | 404.45 | 23.6081 | 18 | 1080.80 | 0.2044 |
| 4 | 525.06 | 0.6330 | 19 | 1245.77 | 0.0000 |
| 5 | 525.13 | 0.6323 | 20 | 1314.07 | 0.0000 |
| 6 | 710.12 | 0.0007 | 21 | 1400.32 | 10.6617 |
| 7 | 710.23 | 0.0000 | 22 | 1400.34 | 10.6347 |
| 8 | 732.36 | 60.0984 | 23 | 1492.47 | 494.3203 |
| 9 | 864.56 | 0.0000 | 24 | 1492.49 | 494.3069 |
| 10 | 927.88 | 0.0000 | 25 | 2639.79 | 283.7784 |
| 11 | 927.90 | 0.0001 | 26 | 2639.84 | 283.7734 |
| 12 | 937.16 | 235.9039 | 27 | 2649.74 | 0.0045 |
| 13 | 944.76 | 0.0037 | 28 | 3641.96 | 0.0114 |
| 14 | 0.0038 | 29 | 3643.76 | 39.7821 | |
| 15 | 945.07 | 0.0000 | 30 | 3643.81 | 39.7850 |
This data enables the IR spectrum of benzene to be predicted.
Population Distribution of Borazine
The calculation was run through the HPC system using the optimised Borazine molecule from the previous calculation. The calculation used the "Energy" method and the 6-31G Basis set.
The output of the calculation was published on D-space which is accessible via this link: DOI::10042/22655 .
A summary of the calculation is tabulated below:
| File name | checkpoint_borazine_MO_output |
| File Type | .fch |
| Calculation Type | SP |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| E(RB3LYP) | -242.68458490 a.u. |
| RMS Gradient Norm | 0.00000000 a.u. |
| Dipole Moment | 0.0001(Debye) |
| Point Group | - |
| Job cpu time | - days - hours - minutes - seconds |
MO analysis of Borazine
The calculated HOMO and LUMO MOs are pictured below: ple.jp
| MO | 7 | 20 (HOMO) | 21 (LUMO) |
| Gaussian depiction |  |
 |
|
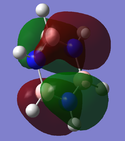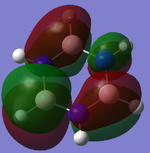
| Energy (a.u.) | -0.88856 | -0.27593 | 0.02423 |
The MO show a mix of the distinctive characteristics of boratabenzene and pyridinium. Electronegative nitrogen has a high electron density whilst electropositive boron has a low electron density. This is backed up by the Charge distribution diagram to the right.
Comparison between Benzene and its analogues
Naturally, there are many different comparisons that could be made between these molecules. However, due to time restraints, I will only be able to consider one. I have chosen to compare the MO 7 as I find it visually represents what is going on in these molecules very well. By substituting carbons with more electronegative and electropositive atoms, the orbitals are being manipulated by these forces, changing the reactivity of the molecule considerably. For example, due to the high electron density around the nitrogen, this benzene analogue is now primed to act as a nucleophile, attacking from the lone pair on the nitrogen. In almost the opposite way as substituting a carbon for a boron to form boratabenzene makes nucleophilic attack at the boron a likely possibility in the right conditions. Most interestingly, in my opionion is the borazine, where 3 nucleophillic centres have been created by the nitrogens adjacent to sites open to nucleophillic attack.
These can be seen in the table below.
| Molecule | Benzene | Boratabenzene | Pyridinium | Borazine |
| MO 7 |  |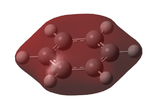
|
|
|
Conclusion
Using Gaussian 5.0 has enabled a huge variety of observations and assumptions to be made without wasting chemicals or exposing anyone to dangerous substances. It is a valuable tool for the analysis of molecular structure, charges and MOs.
References
- ↑ http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year3/3b_understand_opt.html
- ↑ J. Chern. Phys. 96 (5), 1 March 1992 pg3411
- ↑ Acta Chemica Scandivanica A36(1982)125-135
- ↑ D. Grant DD. Heats of formation and bond energies of the H(3-n)BXn compounds for (X ) F, cl, br, I,NH2, OH, and SH). J Phys Chem [bond lengths BHnXn]. 2009(113):777-787.
- ↑ J.F.Stanton,N.S. Kadagathur: J. Chem. Phys., Vol. 102, No. 2, 8 January 1995