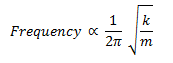Jump to content

Rep:Mod:Linstead

From ChemWiki

Optimisation

BH3 First Optimisation

BH3

File:BH3 (ALF).LOG

Summary

Optimisation Report
Title Result
File Name BH3
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 3-21G
Final Energy (au) -26.46226338
Gradient 0.00020672
Dipole Moment 0.00
Point Group D3H
Duration of Calculation 10 seconds

Convergence Report

         Item               Value     Threshold  Converged?
 Maximum Force            0.000413     0.000450     YES
 RMS     Force            0.000271     0.000300     YES
 Maximum Displacement     0.001610     0.001800     YES
 RMS     Displacement     0.001054     0.001200     YES
 Predicted change in Energy=-1.071764D-06
 Optimization completed.
    -- Stationary point found.

BH3 Second Optimisation

BH3

File:BH3 II.LOG

Summary

Optimisation Report
Title Result
File Name BH3_II
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Final Energy (au) -26.61532363
Gradient 0.00000296
Dipole Moment 0.00
Point Group D3H
Duration of Calculation 8 seconds

Convergence Report

    Item               Value     Threshold  Converged?
 Maximum Force            0.000006     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000023     0.001800     YES
 RMS     Displacement     0.000015     0.001200     YES
 Predicted change in Energy=-2.008855D-10
 Optimization completed.
    -- Stationary point found.

TlBr3

DSpace Report

http://dx.doi.org/10042/23340

Summary

Optimisation Report
Title Result
File Name TlBr3_LOG_ALF
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set LANL2DZ
Final Energy (au) -91.21812851
Gradient 0.00000090
Dipole Moment 0.00
Point Group D3H
Bond Length (Å) 2.65095
Bond Angle (deg) 120
Duration of Calculation 19.6 seconds

Convergence Report

          Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000022     0.001800     YES
 RMS     Displacement     0.000014     0.001200     YES
 Predicted change in Energy=-6.084023D-11
 Optimization completed.
    -- Stationary point found.

Literature bond lengths put the Tl-Br bond at 2.5122 Å [1], which means the value given by this model, 2.65095 Å is reasonable. The variation between my modeled values and the experimental values arise due to the limits of using only a few wave functions and small basis sets.

Optimisation BBr3

DSpace Report

http://dx.doi.org/10042/23338

Summary

Optimisation Report
Title Result
File Name BBr3_LOG_ALF
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set Gen
Final Energy (au) -64.43645253
Gradient 0.00012323
Dipole Moment 0.00
Point Group D3H
Bond Length (Å) 1.933
Bond Angle (deg) 120
Duration of Calculation 31.5 seconds

Convergence Report

         Item               Value     Threshold  Converged?
 Maximum Force            0.000246     0.000450     YES
 RMS     Force            0.000161     0.000300     YES
 Maximum Displacement     0.001151     0.001800     YES
 RMS     Displacement     0.000754     0.001200     YES
 Predicted change in Energy=-4.716315D-07
 Optimization completed.
    -- Stationary point found.

Frequency Analysis

BH3

File:BH3 II FREQ.LOG

Vibrational Frequencies Summary

Low frequencies ---   -0.9432   -0.8611   -0.0054    5.7455   11.7246   11.7625
 Low frequencies --- 1162.9963 1213.1826 1213.1853


Vibrational Frequencies Summary
# Form of Vibration Frequency Intensity Symmetry

D3h Point Group

1
The Hydrogen atoms move in and out of the plane of the molecule together. The Boron atom moves in and out of the plane in the opposite direction to the Hydrogen atoms.		 1163 92.5
A2"
2
The symmetric stretch of two Hydrogen atoms in the plane of the molecule, while the third Hydrogen atom and the Boron move linearly together in the opposite direction.		 1213 14
E'
3
Similar to stretching mode 2. but the Boron atom does not move.The Hydrogen atoms are rocking, with one opposing the motion of the others (antisymmetric)		 1213 14
E'
4
A totally symmetric stretch, the boron atom remains in place while the hydrogen atoms move together in and out, all in the same plane.		 2582 0
A1' Totally Symmetric
5
A Hydrogen atom stays still while the other two atoms move in an asymmetric stretch in the plane, i.e. in opposite directions. The Hydrogen - Boron bond from the stationary Hydrogen moves slightly.		 2715 126.3
E'
6
A symmetric stretch of two Hydrogens coupled with the asymmetric stretch of the other, i.e. opposing the direction of motion of the two. The Boron atom remains stationary		 2715 126.3
E'

IR Spectrum

A computed IR spectrum of the calculated molecule is included:

There appear to be only 3 peaks rather than 6 because the totally symmetric stretch does not give a change in dipole, and therefore does not appear. The degenerate peaks appear at the same energy, and thus are not distinguishable. This means you only see 3 distinguishable peaks.

TlBr3

DSpace Report

http://dx.doi.org/10042/23392

Vibrational Frequencies Summary

Low frequencies ---   -3.4213   -0.0026   -0.0004    0.0015    3.9367    3.9367
 Low frequencies ---   46.4289   46.4292   52.1449


Vibrational Frequencies Summary
# Form of Vibration Frequency Intensity Symmetry

D3h Point Group

1
Symmetric scissoring action of 2 Bromine atoms in plane of molecule. The other Bromine atom and the Thallium move in the opposing direction to the other atoms in the same plane.		 46 4
E'
2
The central Thallium atom remains stationary while 2 of the Bromine atoms wag in the plane of the molecule in one direction and the other in the other direction. (asymmetric wag)		 46 4
E'
3
All Bromine atoms move out of the plane of the molecule together in the opposite direction to the Thallium atom (symmetric twist)		 52 6
A2"
4
All Br atoms move in and out together in the plane, the Thallium atom remains stationary (symmetric stretch)		 165 0
A1' Totally Symmetric
5
A single Br atom remains in position with an asymmetric stretching motion for the other two Bromines, leading to the Tl atom moving a small amount in the opposite direction (assymetric stretch)		 211 25
E'
6
Two Bromine atoms move concertedly in a stretching motion, the third Bromine atom stretches in the opposing direction with little movement of the central atom in space (assymetric stretch)		 211 25
E'

IR Spectrum

A computed IR spectrum of the calculated molecule is included:


Comparison of IR frequencies in the isostructural compounds TlBr3 and BH3

Vibrational Frequencies
# TlBr3 BH3
1 46 E' 1163 A2"
2 46 E' 1213 E'
3 52 A2" 1213 E'
4 165 A1' 2582 A'1
5 211 E' 2715 E'
6 211 E' 2715 E'

The large difference in the frequency values between BH3 and TlBr3 indicates the large difference in mass and also the differing in strength of the bonds within the molecule.

The equation that relates mass of the system and the frequency is given below:

There is also the fact that the force constant will be different in each system, because boron and hydrogen are smaller than thallium and bromide, the bonds will be shorter and stiffer, giving a larger force constant. This will also serve to increase the frequency of the BH3 stretches in comparison to the TlBr3.

There has been a reorganisation of stretching modes, in that the A2" is the lowest energy mode for the BH3, but the A2" comes after the two E' modes in the TlBr3.

The spectra are similar in that there are two peaks much smaller than the third, due to degenerate stretches.

Optimisation and Frequenc Analysis Methods

The molecules must be optimised using exactly the same basis sets and methods, so that the assumptions used in each case are the same. If you were to use different basis sets for the same molecule it would give us different minima and differing stretching frequencies.

The frequency analysis allows us not only to determine that we have found a minima, by minimising the low frequencies, but also allow us to see stretching modes that would otherwise not appear on a spectra, because of being totally symmetric, not changing the dipole moment.

The low frequencies that are shown in the .log file are the "-6" in the 3N-6 stretching modes.

Comparison of Bond Lengths in BH3, BBr3 and TlBr3

Bond Lengths of BH3, TlBr3 and BBr3
Molecule Bond length / Å
BH3 1.19
TlBr3 2.65
BBr3 1.93


The BH3 is the smallest molecule, with both the atoms involved being very small. This results in a far smaller bond length than even the BBr3. The BBr3 has three bromide atoms, each of which is far far greater in size than a hydrogen. The difference in bond lengths is also down to the fact that the valence shell for the bromide is far more diffuse than that of the hydrogen, and that there are three lone pairs on the bromide atom, each taking up space. The same logic applies to the TlBr3, where the thallium is both larger and has a more diffuse valence shell than the boron. The atoms themselves have differing covalent radii, and when you look at these, the trend is the same.


Atomic Radii of H, B, Br, Tl.
Molecule Atomic Radius [2]/ Å
H 0.32
B 0.84
Br 1.17
Tl 1.44

Overall, the steric bulk of the constituent atoms along with their electronegativity makes up for the difference in bond lengths.

What is a bond?

On Gaussview, a bond is determined by length. Whether the distance between two atoms is within a set "bond condition." This leads to some confusion when Gaussview appears to show no bond between two atoms that are in fact bonded. This is because the bond length falls outside what Gaussview calls a bond. It is in fact the overlap of orbitals that make up a bond, and the IUPAC definition of a bond is "A region of relatively high electron density between nuclei which arises at least partly from sharing of electrons and gives rise to an attractive force and characteristic internuclear distance." [3] Using this as our guide, we can see that a bond should be solved using quantum mechanics to find the electron density between two atoms. This means that a bond does not suddenly come into being, as Gaussview appears to show, but increases its bonding character as the atoms approach from infinitely far apart.

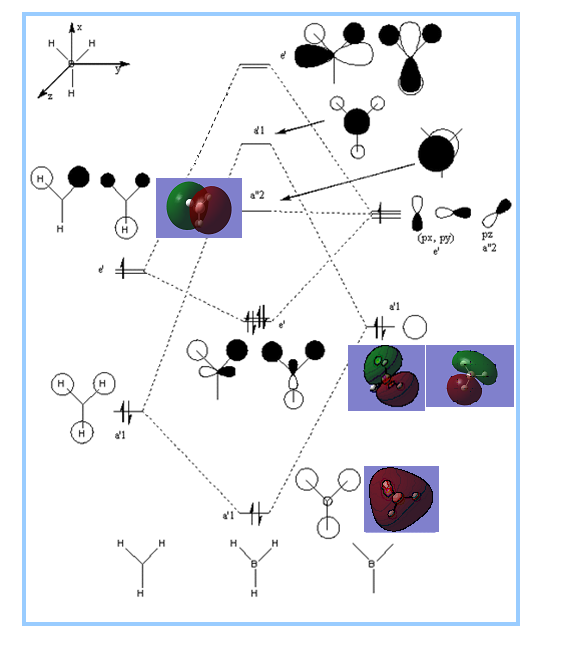
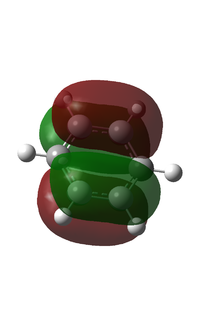
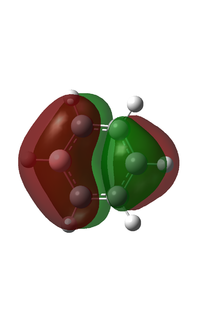
Molecular orbitals

BH3

DSpace Report

http://dx.doi.org/10042/23401

MO Diagram

NH3

Optimisation of NH3 molecule:

File:NH3 ALF II.LOG

Optimisation Report
Title Result
File Name NH3_ALF_II
File Type .log
Calculation Type FOPT
Calculation Method RHF
Basis Set 6-31G(d,p)
Final Energy (au) -56.19554454
Gradient 0.00010676
Dipole Moment (Debye) 1.8
Point Group C1
Bond Length (Å) 1.000
Bond Angle (deg) 107.6
Duration of Calculation 11 seconds 
         Item               Value     Threshold  Converged?
 Maximum Force            0.000200     0.000450     YES
 RMS     Force            0.000124     0.000300     YES
 Maximum Displacement     0.000478     0.001800     YES
 RMS     Displacement     0.000328     0.001200     YES
 Predicted change in Energy=-1.231704D-07
 Optimization completed.
    -- Stationary point found.

Frequency Analysis:

File:NH3 ALF II FREQ.LOG 

 Low frequencies ---  -52.9939  -51.3795  -49.1847   -0.0016    0.0013    0.0014
 Low frequencies --- 1141.4485 1810.4326 1810.6379

Re-Optimisation and Frequency Analysis:

File:NH3 ALF II FREQA.LOG

Calculation Report
Title Result
File Name NH3_ALF_II_FREQA
File Type .log
Calculation Type FOPT
Calculation Method RHF
Basis Set 6-31G(d,p)
Final Energy (au) -56.19554465
Gradient 0.00000256
Dipole Moment (Debye) 1.8
Point Group C1
Bond Length (Å) 1.000
Bond Angle (deg) 107.6
Duration of Calculation 3 seconds 
 Low frequencies ---   -6.0649   -5.1190   -3.1423   -0.0014    0.0012    0.0018
 Low frequencies --- 1142.1708 1810.8159 1810.8163

Further Re-optimisation

The previous optimisations were carried out with the hartree fock energy, which was incorrect. A further optimisation was run with the correct energy set.

File:NH3 ALF II FREQA FINAL.LOG

Calculation Report
Title Result
File Name NH3_ALF_II_FREQA_Final
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Final Energy (au) -56.55776872
Gradient 0.00000326
Dipole Moment (Debye) 1.8
Point Group C1
Bond Length (Å) 1.02
Bond Angle (deg) 105.7
Duration of Calculation 13 seconds 
 Low frequencies ---   -3.7752    0.0011    0.0013    0.0013    5.2394    7.0728
 Low frequencies --- 1089.3784 1693.9290 1693.9383

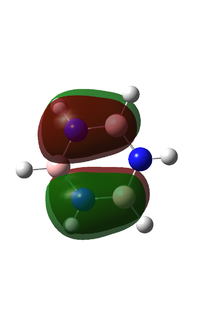
MO Analysis

Calculation Report
Title Result
File Name NH3_ALF_II_MO
File Type .log
Calculation Type SP
Calculation Method RHF
Basis Set 6-31G(d,p)
Final Energy (au) -56.19554465
Gradient 0.00000256
Dipole Moment (Debye) 1.8
Point Group C1
Bond Length (Å) 1.000
Bond Angle (deg) 107.6
Duration of Calculation 3 seconds

The pictures of the MOs are displayed below:


MO2 MO3 MO4 MO5 MO6

NBO Analysis

Colour Range: -1.131 → 1.131

The specific charge for the Nitrogen is -1.131, and each Hydrogen is +0.377, so the molecule is neutrally charged.


NH3BH3

File:NH3BH3 ALF.LOG

Optimisation Report
Title Result
File Name NH3BH3_ALF
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Final Energy (au) -83.22468957
Gradient 0.00005842
Dipole Moment (Debye) 5.565
Point Group C1
Bond Length N-B (Å) 1.668
Lit. [4] Bond Length N-B (Å) 1.601
Duration of Calculation 55 seconds

File:NH3BH3 ALF FREQ.LOG

Optimisation Report
Title Result
File Name NH3BH3_ALF_FREQ
File Type .log
Calculation Type FREQ
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Final Energy (au) -83.22468990
Gradient 0.00005729
Dipole Moment (Debye) 5.565
Point Group C1
Bond Length N-B (Å) 1.668
Lit. [4] Bond Length N-B (Å) 1.601
Duration of Calculation 39 seconds

File:NH3BH3 ALF FREQ II.LOG

Optimisation Report
Title Result
File Name NH3BH3_ALF_FREQ
File Type .log
Calculation Type FREQ
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Final Energy (au) -83.22468904
Gradient 0.00000124
Dipole Moment (Debye) 5.565
Point Group C1
Bond Length N-B (Å) 1.668
Lit. [4] Bond Length N-B (Å) 1.601
Duration of Calculation 1 minute 25 seconds


Instead of looking at the total energy of the molecule, I have decided to look at the free energy, including the entropic term. This gives you a lower value, since you are of course going from two molecules to one, and losing entropy. This takes up energy and thus the free energy of the bond is lower than the ~135kJ/mol that is expected. 

Free Energy: NH3BH3 @ 298K: -83.178118
Free Energy: NH3 @ 298K: -56.542403
Free Energy: BH3 @ 298K: -26.606441
Free Energy of reaction: -0.029274 au
Free Energy of reaction kJ/mol: -76.86

Free Energy of dissociation @ 298K: 80kJ/mol

Investigating Aromaticity

Benzene

Benzene is the standard with which all aromatic molecules are compared. The molecular orbitals however are not as simple as first imagined.

Optimisation and Frequency Analysis

File:Benzene ALF 1.log

Optimisation Report
Title Result
File Name Benzene_ALF_1
File Type .log
Calculation Type Freq
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Final Energy (au) -232.25820551
Gradient 0.00009550
Dipole Moment (Debye) 0
Point Group C1
Bond Length C-C (Å) 1.396
Bond Length C-H (Å) 1.086
Bond Angle (deg) 120
Duration of Calculation 4minutes 35 seconds 


       Item               Value     Threshold  Converged?
 Maximum Force            0.000212     0.000450     YES
 RMS     Force            0.000085     0.000300     YES
 Maximum Displacement     0.000991     0.001800     YES
 RMS     Displacement     0.000315     0.001200     YES
 Predicted change in Energy=-5.157454D-07
 Optimization completed.
    -- Stationary point found.



 Low frequencies ---  -17.2824  -14.5873   -9.6634   -0.0008   -0.0004    0.0003
 Low frequencies ---  413.7969  414.4697  620.8546

MO Analysis

File:BENZENE ALF MO.LOG

File:Benzene ALF MO.pdf

Boratabenzene

Optimisation and Frequency Analysis

File:BORATA ALF I.LOG

Optimisation Report
Title Result
File Name Pyri_ALF_1
File Type .log
Calculation Type Freq
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Final Energy (au) -219.02052984
Gradient 0.00015815
Dipole Moment (Debye) 2.85
Point Group C1
Bond Length C-C (Å) 1.40
Bond Length C-B (Å) 1.514
Average Bond Angle C-C-C (deg) 121
Bond Angle C-B-C (deg) 115.0
Duration of Calculation 3minutes 16 seconds 
         Item               Value     Threshold  Converged?
 Maximum Force            0.000160     0.000450     YES
 RMS     Force            0.000069     0.000300     YES
 Maximum Displacement     0.000861     0.001800     YES
 RMS     Displacement     0.000321     0.001200     YES
 Predicted change in Energy=-7.184243D-07
 Optimization completed.
    -- Stationary point found.

 Low frequencies ---  -13.1331   -0.0005   -0.0001    0.0006   15.0724   18.1749
 Low frequencies ---  371.3449  404.2342  565.2519

MO Analysis

File:BORATA ALF MO.LOG

Further analysis will follow when comparing to other aromatic systems.

Pyridinium

Optimisation and Frequency Analysis

File:PYRI ALF I.LOG


Optimisation Report
Title Result
File Name Pyri_ALF_1
File Type .log
Calculation Type Freq
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Final Energy (au) -248.66807396
Gradient 0.00003904
Dipole Moment (Debye) 1.87
Point Group C1
Bond Length C-C (Å) 1.398
Bond Length C-N (Å) 1.352
Bond Angle C-C-C (deg) 119.3
Bond Angle C-N-C (deg) 123.0
Duration of Calculation 3minutes 16 seconds

A jmol file can be found 

      Item               Value     Threshold  Converged?
 Maximum Force            0.000064     0.000450     YES
 RMS     Force            0.000023     0.000300     YES
 Maximum Displacement     0.000836     0.001800     YES
 RMS     Displacement     0.000186     0.001200     YES
 Predicted change in Energy=-7.441419D-08
 Optimization completed.
    -- Stationary point found.



Low frequencies ---   -7.1994   -0.0007    0.0003    0.0006   17.3377   18.5318
 Low frequencies ---  392.4552  404.0618  620.4715

MO Analysis

File:PYRI ALF MO.LOG

Further analysis will follow when comparing to other aromatic systems.

Borazine

Optimisation and Frequency Analysis

File:BORAZINE ALF I.LOG


Optimisation Report
Title Result
File Name Borazine_ALF_I
File Type .log
Calculation Type Freq
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Final Energy (au) -242.68459771
Gradient 0.00002102
Dipole Moment (Debye) 0
Point Group C1
Bond Length B-N(Å) 1.431
Bond Length B-H (Å) 1.195
Bond Length N-H (Å) 1.010
Bond Angle B-N-B (deg) 122.9
Bond Angle N-B-N (deg) 117.1
Duration of Calculation 3minutes 15 seconds 
         Item               Value     Threshold  Converged?
 Maximum Force            0.000072     0.000450     YES
 RMS     Force            0.000018     0.000300     YES
 Maximum Displacement     0.000416     0.001800     YES
 RMS     Displacement     0.000156     0.001200     YES
 Predicted change in Energy=-4.391525D-08
 Optimization completed.
    -- Stationary point found.



 Low frequencies ---  -11.2213   -0.0012   -0.0007   -0.0006    8.2077    9.4691
 Low frequencies ---  288.6131  290.4743  404.3232

MO Analysis

File:BORAZINE ALF MO.LOG

Further analysis will follow when comparing to other aromatic systems.

Aromatic Comparison

NBO Charge Distribution

NBO Charge Analysis
Molecule Coloured Charge Diagram Numbered Charge Diagram Description
Benzene Carbons are negatively charged, as compared to the positive charge of the hydrogens. Narrow overall range, (±0.239)
Boratabenzene Boron positively charged; carbons negative and decreasing in charge away from the boron. Hydrogens are positive, however the hydrogen bonded to the electropositive boron appears nearly neutral. There is an overall negative charge, born out by the sum of all charges, and an average charge range, (±0.588)
Pyridinium Nitrogen has a large negative charge and is surrounded by positively charged carbons and hydrogens. The other carbons as usual are negative, there is an overall positive charge. Average charge range (±0.483)
Borazine All nitrogens are strongly negative and all borons are positive. Nitrogen atoms are more charged, boron atoms less so. Hydrogens switch between neutral and positively charged, when they are bonded to boron and nitrogen respectively. Overall neutral, so charges cancel out. Wide charge range (±1.102)


MO Comparison

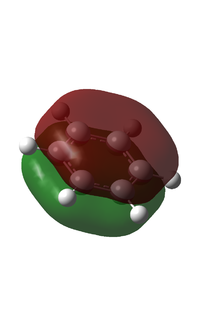
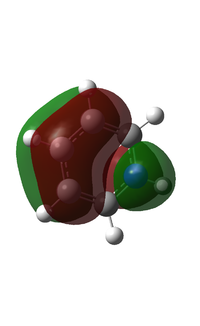
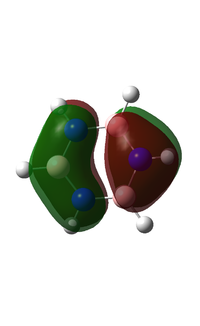
I have chosen to compare the fully p based MOs.

MO 17

Molecular Orbital Analysis for MO 17
Molecule Benzene Boratabenzene Pyridinium Borazine
Molecular Orbital
Energy / Hartree -0.3600 -0.1321 -0.6406 -0.3613
Comparison Even distribution of pi electrons Electron distribution slightly skewed away from boron atom Electron distribution slightly skewed onto nitrogen Uneven electron distribution; more on nitrogen than boron. Lower order of symmetry (reduction of principle axis C3 from C6)

MO 20

Molecular Orbital Analysis for MO 20
Molecule Benzene Boratabenzene Pyridinium Borazine
Molecular Orbital
Energy / Hartree -0.2469 -0.0349 -0.5090 -0.2760
Comparison Even distribution of pi electrons in two phases Electron distribution ever so slightly skewed away from boron atom Electron distribution skewed away from carbons next to nitrogen. Uneven electron distribution; more on set with more nitrogen than boron than on the set with only one nitrogen atom.

MO 21

Molecular Orbital Analysis for MO 21
Molecule Benzene Boratabenzene Pyridinium Borazine
Molecular Orbital
Energy / Hartree -0.2469 +0.0109 -0.4790 -0.2759
Comparison Even distribution of pi electrons in two phases There is slightly less electron distributed on the boron atom than on the carbon atom opposite, but overall this is a fairly even distribution Similar in appearance to MO 20 for boratabenzene, with the electron distribution skewed towards the nitrogen. The electron distribution is shifted towards the side of the orbitals with the nitrogen.

Analysis

The most important point that is visible in all the MOs, is that the boron, being less electronegative than the carbon, has less electron density on it. This logic applies to the carbon as compared to the more electronegative nitrogen. The energies of the orbitals also became increasingly negative along the same scale, boron < carbon < nitrogen. Having a more electronegative heteroatom in the system lowers the energy of that system. When both nitrogen and boron atoms were present, in the borazine, the effects of each were vaguely cancelled out, with the energies being similar, although slightly more negative in all cases, to the energy of benzene. We can assume that the lowering in energy because of the inclusion of the electronegative element is due to its more readily accepting electrons. This would lower bonding orbitals and raise antibonding orbitals.

Generally, the order of MOs was unchanged from molecule to molecule, especially in the frontier region. The degeneracy of the orbitals was similar in the four, but with some small differences. Benzene is the most degenerate of the four, and is also the most symmetrical, whereas boratabenzene and pyridinium share degeneracy and symmetry. This leads us to the conclusion that symmetry and degeneracy are related.

Probably the most interesting thing to be gained from this exercise was that using a small basis set and a simple method, an accurate picture of the orbitals was derived. This shows that using quantum mechanics you can solve for most/any molecule to give a good approximation.

References

  1. ↑ J.Glaser, G.Johansson, Acta Chemica Scandanavica, 1982, 36A, 125-35
  2. ↑ CRC Handbook 93rd edition
  3. ↑ P.Muller, Pure & Appl. Chem, 1994, 66 (No.5), 1077-1184
  4. ↑ 4.0 4.1 4.2 R.Boese, N.Niederprum, D.Blaser, Molecules in Natural Science and Medicine , 1991, 103
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:Linstead&oldid=817381"