Rep:Mod:Lemon789
Optimisation of a molecule
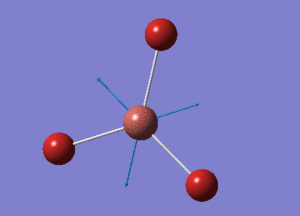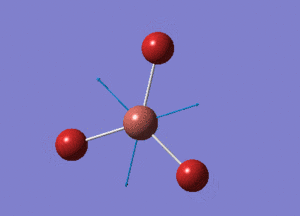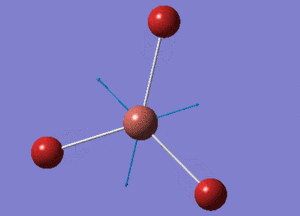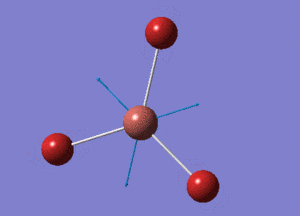
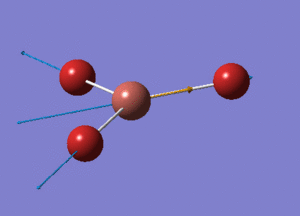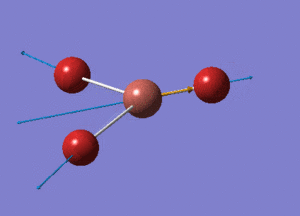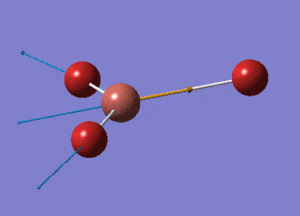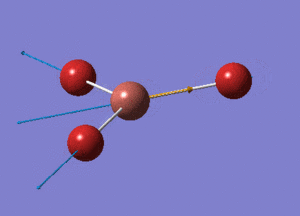
BH3 Optimisation with Basis Set = 3-21G
Calculation Type = FOPT
Calculation Method = RB3LYP
Basis Set = 3-21G
E(RB3LYP) = -26.46226338 a.u.
RMS Gradient Norm = 0.00020672 a.u.
Dipole Moment = 0.0000 Debye
Point Group = D3H
Job cpu time: 0 days 0 hours 0 minutes 10.0 seconds.
Item Value Threshold Converged?
Maximum Force 0.000413 0.000450 YES
RMS Force 0.000271 0.000300 YES
Maximum Displacement 0.001610 0.001800 YES
RMS Displacement 0.001054 0.001200 YES
Predicted change in Energy=-1.071764D-06
Optimization completed.
-- Stationary point found.
BH3 Optimisation with Basis Set = 6-31G(d,p)
Calculation Type = FOPT
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
E(RB3LYP) = -26.61532363 a.u.
RMS Gradient Norm = 0.00000235 a.u.
Dipole Moment = 0.0000 Debye
Point Group = D3H
Job cpu time: 0 days 0 hours 0 minutes 4.0 seconds.
Item Value Threshold Converged?
Maximum Force 0.000005 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.000019 0.001800 YES
RMS Displacement 0.000012 0.001200 YES
Predicted change in Energy=-1.304899D-10
Optimization completed.
-- Stationary point found.
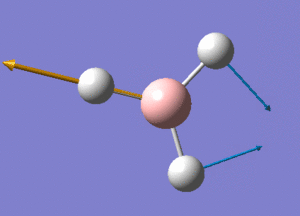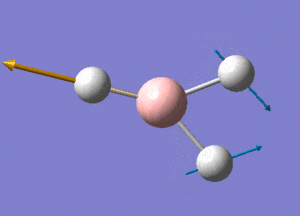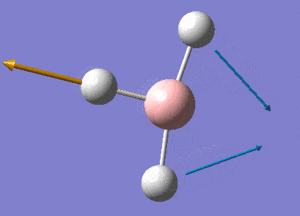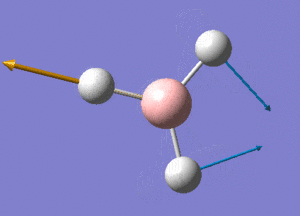
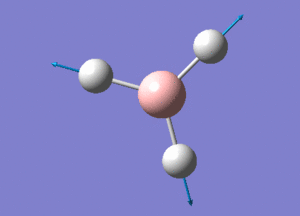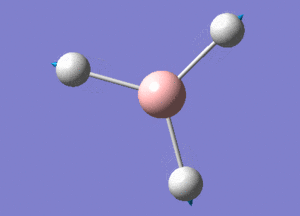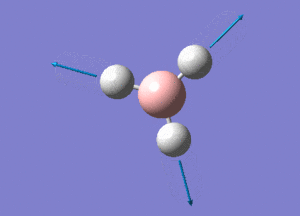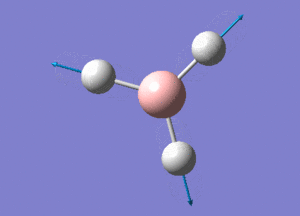
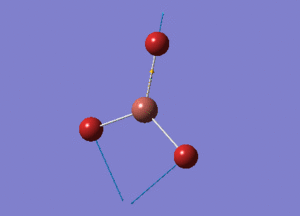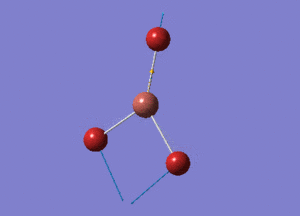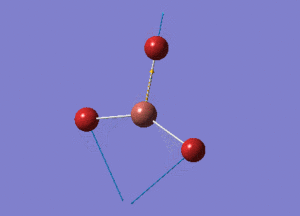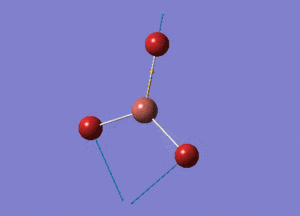
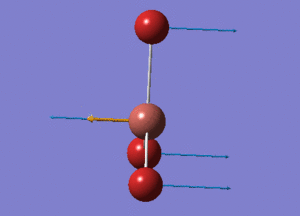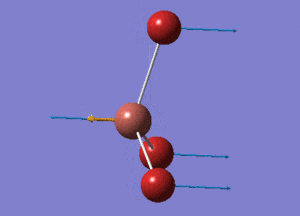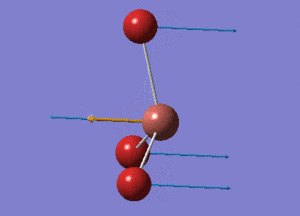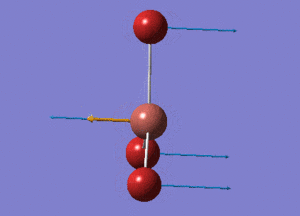
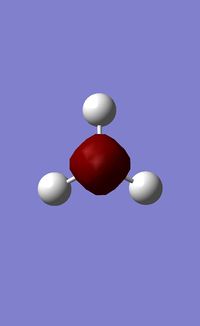
BH3 Structure
Total energy for 3-21G optimised structure: -26.46226338 a.u.
Total energy for 6-31G optimised structure: -26.61532363 a.u.
B-H bond distance = 1.19232 Å
H-B-H bond angle = 120o
BBr3 Optimisation using 6-31G(d,p) basis set and pseudo potentials
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set Gen
E(RB3LYP) -64.43645296 a.u.
RMS Gradient Norm 0.00000382 a.u.
Dipole Moment 0.0000 Debye
Point Group D3H
Job cpu time: 0 days 0 hours 0 minutes 19.8 seconds.
Item Value Threshold Converged?
Maximum Force 0.000008 0.000450 YES
RMS Force 0.000005 0.000300 YES
Maximum Displacement 0.000036 0.001800 YES
RMS Displacement 0.000023 0.001200 YES
Predicted change in Energy=-4.027278D-10
Optimization completed.
-- Stationary point found.
BBr3 Structure
B-Br bond distance = 1.93396 Å
Br-B-Br bond angle = 120o
TlBr3 Optimisation using pseudo potentials
Calculation Type = FOPT
Calculation Method = RB3LYP
Basis Set = LANL2DZ
Total Energy = -91.21812851 a.u.
RMS Gradient Norm = 0.00000090 a.u.
Dipole Moment = 0.0000 Debye
Point Group = D3H
Job cpu time: 0 days 0 hours 0 minutes 9.0 seconds.
Item Value Threshold Converged?
Maximum Force 0.000002 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000022 0.001800 YES
RMS Displacement 0.000014 0.001200 YES
Predicted change in Energy=-6.084115D-11
Optimization completed.
-- Stationary point found.
TlBr3 Structure
Tl-Br bond distance = 2.65095 Å (lit.: 2.5122 Å [1])
Tl-B-Tl bond angle = 120o
Structure Comparison
BH3 has the smallest bond distance (1.19232 Å), followed by BBr3 (1.93396 Å) and then finally TlBr3 has the longest (2.65095 Å). By directly comparing BH3 and BBr3, the effect on the bond length of introducing a larger ligand into the system can be seen. The Br atom is considerably larger than a H atom, due to an increased atomic mass and larger, more diffuse orbitals. Therefore, the B-Br bond length is considerably longer than the B-H one. As both Br and H have one unpaired elecctron, they will both be held in the same trigonal planar conformation, with all bonds at 120o to each other. However, as Br is more electronegative than H, the B-H bond will be less polar than the B-Br bond.
Changing the central element from B to Tl leads to a substantial increase in the bond distance. This is because the Tl atom is in a much lower period than the B atom, which is a first row element. Consequently, the Tl atom will have much larger and more diffuse orbitals, which will lead the the ligands being held at much longer distances than when they are bonded to B, leading to the longer, weaker bonds seen.
Some structures in gaussview don't have bonds because it draws bonds based on a distance criteria. So an absence of an expected bond indicates that the distance of the bond in question exceeds that of a pre-defined value and doesn't mean that the bond is infact non-existent. A chemical bond is an interaction between two atoms which holds them together to form a molecule. This interaction can be based off electrostatic interactions (such as in an ionic bond), the sharing of the atoms electrons themselves (a covalent bond) or weaker bonds, such a hydrogen bonding and dipole-dipole interactions.
Frequency Analysis
Frequency Analysis of BH3
Calculation Type = FREQ
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
E(RB3LYP) = -26.61532363 a.u.
RMS Gradient Norm = 0.00000237 a.u.
Dipole Moment = 0.0000 Debye
Point Group = D3H
Job cpu time: 0 days 0 hours 0 minutes 9.0 seconds.
Low frequencies --- -0.9033 -0.7343 -0.0054 6.7375 12.2491 12.2824 Low frequencies --- 1163.0003 1213.1853 1213.1880
File:ALEX GILLETT BH3 FREQ.LOG
| No. | Form of the vibration | Frequency / cm-1 | Intensity | Symmetry (Point group D3h) |
| 1 | 
All H's move down into the z-axis, while the central B atom moves in the opposite direction. |
1163 | 92.5478 | Bending out-of-plane A2" |
| 2 | 
2 of the H's move towards each other in the plane, reducing the angle separating them. The other H and B move slightly in the opposite direction. |
1213.19 | 14.0553 | Bending in-plane E' |
| 3 | 
2 of the H's rotate around the central axis, whilst keeping the 120 angle separating them constant. Meanwhile, the other H rotates the opposite way, reducing the 120 angle between it and the H it approaches. The B atom is relatively stationary |
1213.19 | 14.0589 | Bending in-plane E' |
| 4 | 
All the H's move out together in the plane of the molecule in a concerted fashion. The central B atom stays stationary. |
2582.26 | 0 | Totally symmetric stretch A1' |
| 5 | 
One hydrogen moves away from the B center, whilst another moves inwards. The B center moves in sympathy towards the H moving away. Meanwhile, the final H stays stationary. |
2715.43 | 126.3307 | Asymmetrical stretching E' |
| 6 | 
2 H's move away from the B center in a concerted fashion, whilst the remaining H moves in towards the center. The B atom is moves slightly towards this remaining H atom. |
2715.43 | 126.3211 | Asymmetrical stretching E' |
There are 6 different vibrational modes predicted (as would be expected from the 3N-6 rule, where N=4 for BH3). However, there are only 3 peaks observed because vibrations 1+2 and 5+6 are both of the same symmetry label and are therefore degenerate in energy, meaning only 1 peak is seen for each. Furthermore, stretch 4 results in no change in the overall dipole moment, meaning no absorption will be seen for this vibration.
TlBr3 Frequency Analysis
Calculation Type = FREQ
Calculation Method = RB3LYP
Basis Set = LANL2DZ
E(RB3LYP) = -91.21812851 a.u.
RMS Gradient Norm = 0.00000088 a.u.
Dipole Moment = 0.0000 Debye
Point Group = D3H
Job cpu time: 0 days 0 hours 0 minutes 15.8 seconds.
Low frequencies --- -3.4213 -0.0026 -0.0004 0.0015 3.9367 3.9367 Low frequencies --- 46.4289 46.4292 52.1449
| No. | Form of the vibration | Frequency / cm-1 | Intensity | Symmetry (Point group D3h) |
| 1 | 
2 of the Br's move towards each other in the plane, reducing the angle separating them. The other Br and Tl move slightly in the opposite direction. |
46.43 | 3.6867 | Bending in-plane E' |
| 2 | 
2 of the Br's rotate around the central axis, whilst keeping the 120 angle separating them constant. Meanwhile, the other Br rotates the opposite way, reducing the 120 angle between it and the Br it approaches. The Tl atom moves in sympathy. |
46.43 | 3.6867 | Bending in-plane E' |
| 3 | 
All Br's move down into the z-axis, while the central Tl atom moves in the opposite direction. |
52.14 | 5.8466 | Bending out-of-plane A2" |
| 4 | 
All the Br's move out together in the plane of the molecule in a concerted fashion. The central Tl atom stays stationary. |
165.27 | 0 | Totally symmetric stretch A1' |
| 5 | 
One Br moves away from the Tl center, whilst another moves inwards. The Tl center moves in sympathy towards the Br moving away. Meanwhile, the final Br stays stationary. |
210.69 | 25.4830 | Asymmetrical stretching E' |
| 6 | 
2 Br's move away from the Tl center in a concerted fashion, whilst the remaining Br moves in towards the center. The Tl atom moves in the opposite direction to this remaining Br. |
210.69 | 25.4797 | Asymmetrical stretching E' |
For the same reasons as in BH3,6 vibrational bands are predicted, but only 3 are seen.
Comparison of the vibrational spectra of BH3 and TlBr3
The most obvious difference between the vibrational spectra is the variation in the wavenumbers of the different vibrational modes. The BH3 vibrations are at a much higher wavenumbers than those for the TlBr3 due to both the difference in the reduced mass and the relative bond strengths. It is known that having a smaller reduced mass leads to a higher vibrational frequency and therefore a higher wavenumber. As well as this, the Tl-Br bonds are much weaker than the B-H bonds, due to the presence of much larger, more diffuse orbitals which lead to a poorer overlap and a weaker bond, culminating in a lower vibrational frequency.
Secondly, a reordering of the vibrational modes can clearly be seen. For BH3, the modes are in the order A2", E', E', A1', E', E', while for TlBr3, they are in the order E',E', A2", A1' E', E': the lower E' and the A2" modes have been swapped round. This could be due to increased mass of the Br over the H, which makes the A2" symmetrical bending motion require more energy than the E' rocking and scissoring vibrations.
The spectra are similar because they have 3 peaks (as explained earlier), 1 of which is a lower frequency bending mode and the other 2 higher frequency stretching modes.
The same method and basis set must be used for the optimisation and frequency analysis because the potential energy surfaced probed varies between the different basis sets and methods: using different ones would render the frequency calculation invalid.
The frequency analysis is carried out to confirm that a minimum energy point in the potential energy curve has been found and not just a plateau. Furthermore, it also provides useful information about the vibrational spectra of a molecule.
Low frequencies represent the motion of the centre of mass of the molecule. It is known that a molecule has 3N-6 vibrational frequencies and here, the "-6" represents the low frequencies.
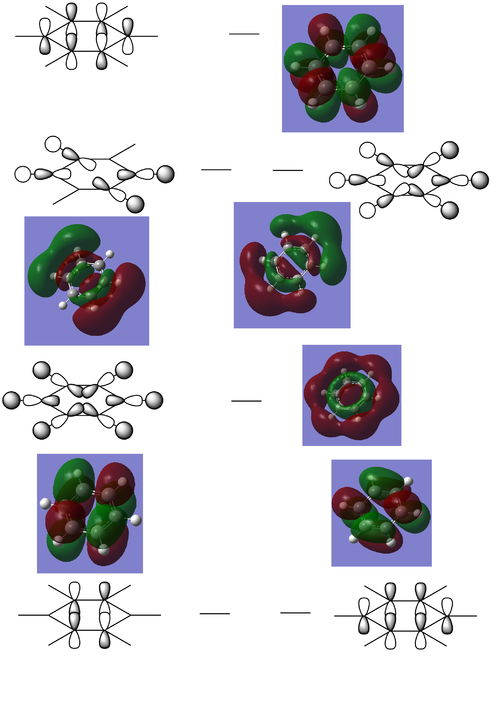
BH3 MO Analysis
Calculation Type = SP
Calculation Method = RB3LYP
Basis Set = 6-31G(D,P)
Total Energy = -26.61532363 a.u.
RMS Gradient Norm = 0.00000000 a.u.
Dipole Moment = 0.0000 Debye
Point Group = D3H
It is apparent that the LCAO MO's mimic the the "real" MO's produced from calculations rather closely, with all the calculated lobes matching up extremely well with what is quickly predicted from LCAO theory. This suggests that MO theory is a comparatively quick and quite accurate way to model the MO's of a simple molecule.
NH3 Analysis
Optimisation of NH3
File Type = .log
Calculation Type = FOPT
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
E(RB3LYP) = -56.55776872 a.u.
RMS Gradient Norm = 0.00001217 a.u.
Dipole Moment = 1.8469 Debye
Point Group = C1
Job cpu time: 0 days 0 hours 0 minutes 15.0 seconds.
Job cpu time: 0 days 0 hours 0 minutes 9.0 seconds.
Item Value Threshold Converged?
Maximum Force 0.000014 0.000450 YES
RMS Force 0.000010 0.000300 YES
Maximum Displacement 0.000215 0.001800 YES
RMS Displacement 0.000114 0.001200 YES
Predicted change in Energy=-4.984435D-09
Optimization completed.
-- Stationary point found.
Frequency Analysis of NH3
File Type = .log
Calculation Type = FREQ
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
E(RB3LYP) = -56.55776872 a.u.
RMS Gradient Norm = 0.00001213 a.u.
Dipole Moment = 1.8469 Debye
Point Group = C1
Job cpu time: 0 days 0 hours 0 minutes 14.0 seconds.
Low frequencies --- -10.7836 -6.7089 -0.0018 -0.0016 -0.0009 10.4306 Low frequencies --- 1089.7963 1693.9573 1693.9707
MO's of NH3
top left: lowest energy MO; top right: highest)
NBO Analysis NH3
Charge on N: -1.125 Charge on H: 0.375
Colour range: Green: -1.125 to Red: 1.125
NH3BH3 Analysis
Item Value Threshold Converged?
Maximum Force 0.000139 0.000450 YES
RMS Force 0.000062 0.000300 YES
Maximum Displacement 0.000638 0.001800 YES
RMS Displacement 0.000334 0.001200 YES
Predicted change in Energy=-1.946571D-07
Optimization completed.
-- Stationary point found.
File Type = .log
Calculation Type = FOPT
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
E(RB3LYP) = -83.22468889 a.u.
RMS Gradient Norm = 0.00006552 a.u.
Dipole Moment = 5.5654 Debye
Point Group = C1
Job cpu time: 0 days 0 hours 0 minutes 17.0 seconds.
File:NH3BH3 OPTIMISATION V2.LOG
File Type = .log
Calculation Type = FREQ
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
E(RB3LYP) = -83.22468890 a.u.
RMS Gradient Norm = 0.00006549 a.u.
Dipole Moment = 5.5654 Debye
Point Group = C1
Job cpu time: 0 days 0 hours 1 minutes 39.0 seconds.
Low frequencies --- -0.0010 -0.0005 0.0010 17.2979 17.8690 39.0596 Low frequencies --- 266.1042 632.2781 639.4108
E(NH3)= -56.55776872 a.u.
E(BH3)= -26.61532363 a.u.
E(NH3BH3)= -83.22468890 a.u.
ΔE=E(NH3BH3)-[E(NH3)+E(BH3)]
ΔE= -83.22468890 -[-83.17309235]
ΔE= -0.05159655 a.u.
ΔE= -135.466752344 KJ/mol
The value obtained is fairly small and negative, indicating that the bond would be quite weak and would be exothermic upon dissociation.
Aromaticity Mini-Project
Benzene
File Type = .log
Calculation Type = FOPT
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
E(RB3LYP) = -232.25820551 a.u.
RMS Gradient Norm = 0.00009549 a.u.
Dipole Moment = 0.0001 Debye
Point Group = C1
Job cpu time: 0 days 0 hours 1 minutes 1.0 seconds.
Item Value Threshold Converged?
Maximum Force 0.000212 0.000450 YES
RMS Force 0.000085 0.000300 YES
Maximum Displacement 0.000991 0.001800 YES
RMS Displacement 0.000315 0.001200 YES
Predicted change in Energy=-5.157454D-07
Optimization completed.
-- Stationary point found.
Low frequencies --- -17.2788 -14.5868 -9.6527 -0.0009 -0.0007 -0.0004 Low frequencies --- 413.7971 414.4697 620.8545
NBO analysis
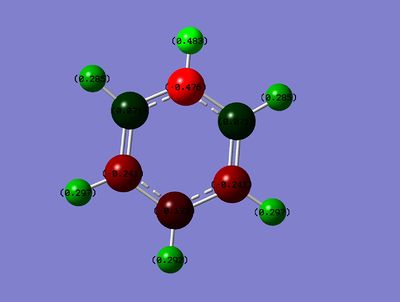
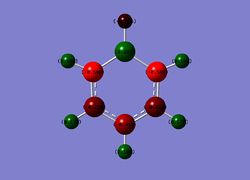
Charge Distribution of Benzene
Range: Green= 0.239; Red= -0.239
Carbon: -0.239
Hydrogen: 0.239
Boratabenzene
Optimisation
File Type = .log
Calculation Type = FOPT
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
E(RB3LYP) = -219.02052984 a.u.
RMS Gradient Norm = 0.00015822 a.u.
Dipole Moment = 2.8465 Debye
Point Group = C1
Job cpu time: 0 days 0 hours 2 minutes 3.0 seconds.
Item Value Threshold Converged?
Maximum Force 0.000159 0.000450 YES
RMS Force 0.000069 0.000300 YES
Maximum Displacement 0.000911 0.001800 YES
RMS Displacement 0.000335 0.001200 YES
Predicted change in Energy=-6.630178D-07
Optimization completed.
-- Stationary point found.
File:BORATABENZENE OPTIMISATION.LOG
Frequency Analysis
File Type = .log
Calculation Type = FREQ
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
E(RB3LYP) = -219.02052984 a.u.
RMS Gradient Norm = 0.00015830 a.u.
Dipole Moment = 2.8465 Debye
Point Group = C1
Job cpu time: 0 days 0 hours 3 minutes 43.0 seconds.
Low frequencies --- -13.1243 -0.0005 -0.0005 -0.0001 15.0607 18.1733 Low frequencies --- 371.3450 404.2340 565.2523
[FILE:BORATABENZENE_FREQ.LOG]]
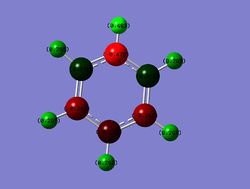
Charge Distribution
Range: Green= 0.588 ; Red= -0.588
B: 0.202
o-C: -0.588
m-C: -0.250
p-C: -0.340
B-H: -0.096
o-H: 0.184
m-H: 0.179
p-H: 0.186
Pyridinium
Optimisation
File Type = .log
Calculation Type = FOPT
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
E(RB3LYP) = -248.66807396 a.u.
RMS Gradient Norm = 0.00003896 a.u.
Dipole Moment = 1.8727 Debye
Point Group = C1
Job cpu time: 0 days 0 hours 2 minutes 3.0 seconds.
Item Value Threshold Converged?
Maximum Force 0.000064 0.000450 YES
RMS Force 0.000023 0.000300 YES
Maximum Displacement 0.000702 0.001800 YES
RMS Displacement 0.000174 0.001200 YES
Predicted change in Energy=-6.897705D-08
Optimization completed.
-- Stationary point found.
Frequency Analysis
File Type = .log
Calculation Type = FREQ
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
E(RB3LYP) = -248.66807396 a.u.
RMS Gradient Norm = 0.00003889 a.u.
Dipole Moment = 1.8727 Debye
Point Group = C1
Job cpu time: 0 days 0 hours 3 minutes 49.0 seconds.
Low frequencies --- -7.2104 -0.0005 -0.0005 -0.0003 17.3406 18.5424 Low frequencies --- 392.4561 404.0617 620.4717
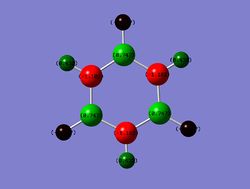
Charge Distribution
Range: Green= 0.483; Red= -0.483
N: -0.476
o-C: 0.071
m-C: -0.241
p-C: -0.122
N-H: 0.483
o-H: 0.285
m-H: 0.297
p-H: 0.292
Borazine
Optimisation
File Type = .log
Calculation Type = FOPT
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
E(RB3LYP) = -242.68459789 a.u.
RMS Gradient Norm = 0.00007128 a.u.
Dipole Moment = 0.0003 Debye
Point Group = C1
Job cpu time: 0 days 0 hours 2 minutes 36.0 seconds.
Item Value Threshold Converged?
Maximum Force 0.000117 0.000450 YES
RMS Force 0.000036 0.000300 YES
Maximum Displacement 0.000327 0.001800 YES
RMS Displacement 0.000104 0.001200 YES
Predicted change in Energy=-1.206131D-07
Optimization completed.
-- Stationary point found.
File:BORAZINE OPTIMISATION.LOG
Frequency Analysis
File Type = .log
Calculation Type = FREQ
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
E(RB3LYP) = -242.68459784 a.u.
RMS Gradient Norm = 0.00007133 a.u.
Dipole Moment = 0.0003 Debye
Point Group = C1
Job cpu time: 0 days 0 hours 3 minutes 43.0 seconds.
Low frequencies --- -11.3055 -0.0012 -0.0010 -0.0002 8.9829 10.9723 Low frequencies --- 288.5038 290.4005 404.0142
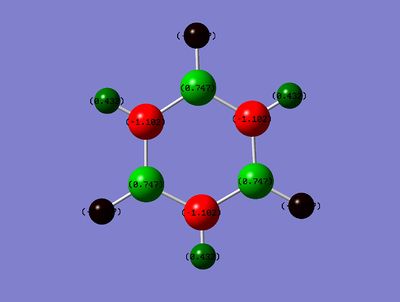
Charge Distribution
Range: Green: 1.102; Red: -1.102
B: 0.747
N: -1.102
B-H: -0.077
N-H: 0.432
Charge Distribution Comparison
| Boratabenzene Anion | Benzene | Pyridinium Cation | Borazine | |
|---|---|---|---|---|
| File:BENZENE MOS 2.LOG | File:BORATABENZENE MOS.LOG | File:PYRIDINIUM MOS.LOG | File:BORAZINE MOS.LOG | |
| Charge distribution |
|
|
|
|
| Overall charge on complex | -1 | 0 | +1 | 0 |
| Charge distribution on atoms | Carbon: -0.239
Hydrogen: 0.239 |
B: 0.202
o-C: -0.588 m-C: -0.250 p-C: -0.340 B-H: -0.096 o-H: 0.184 m-H: 0.179 p-H: 0.186 |
N: -0.476
o-C: 0.071 m-C: -0.241 p-C: -0.122 N-H: 0.483 o-H: 0.285 m-H: 0.297 p-H: 0.292 |
B: 0.747
N: -1.102 B-H: -0.077 N-H: 0.432 |
| Colour Range | Red: -0.239; Green: 0.239 | Red: -0.588; Green: 0.588 | Red: -0.483; Green: 0.483 | Red: -1.102; Green: 1.102 |
The benzene ring can be seen to have an equal charge distribution over the whole molecule with no formal overall charge on the molecule. This originates from the symmetry of all the C's and H's in the molecule which leads to the degeneracy of the charge distribution amongst the atoms.
By comparison, in the boratabenzene analogue, a formal negative charge is introduced to the compound in order to maintain the isoelectronic nature of the system to benzene. This negative charge is most strongly localised on the o-C and the p-C through resonance effects, as can be seen in the NBO analysis, with the o-C having a slightly higher negative charge due to it's proximity to the electropositive B atom. It is worth noting that the charge on the m-C's are almost identical to that in benzene. This is because the o-C insulates this position from the B atom and the fact that there are no resonance effects on the m-C position which could affect the charge distribution. As the system has an overall negative charge, the H's bonded to the C's in the system have a smaller positive charge than in benzene. As expected, the B atom is positively charged, while the B-H has a slightly negative charge associated to it, indicating slight hydride-like character.
In pyridinium, a formal positive charge must be introduced to the system. This positive charge is localised on the o-C and p-C positions due to resonance effects and inductive effects in the case of the o-C position which is adjacent to the N atom. However, both of these positions still have a slightly overall negative charge. Again, the m-C is almost completely unaffected by this overall positive charge on the system, due to the same effects that are discussed above. As the system has an overall positive charge, the H's bonded to the C's in the system have a larger positive charge than in benzene. The N atom has has the expected negative charge, whilst the N-H has a larger positive charge than any of the other H's in the system due to inductive effects from the N atom.
Finally, in borazine, the expected negative charges on N and positive charges on B are seen, due to the large difference in electronegativity. This charge distribution is highly symmetric, as would be expected for a system containing alternating B and N atoms. The N-H's show positive charge and the B-H's a negative charge, as would be expected from a comparison of their relative electronegativites.
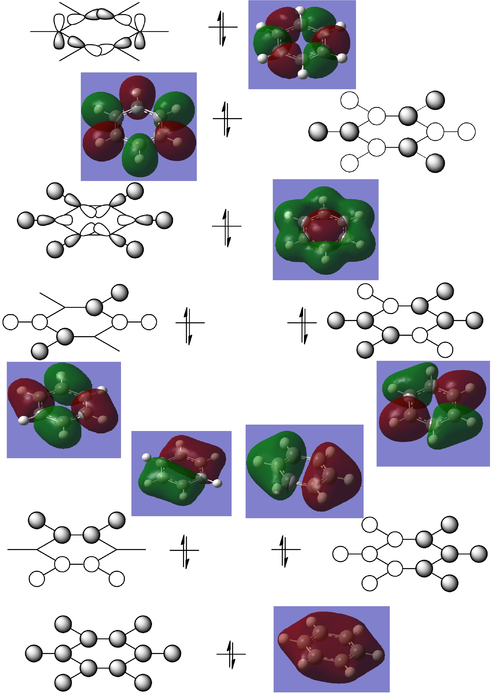
Comparison of Benzene MO's to the analogues
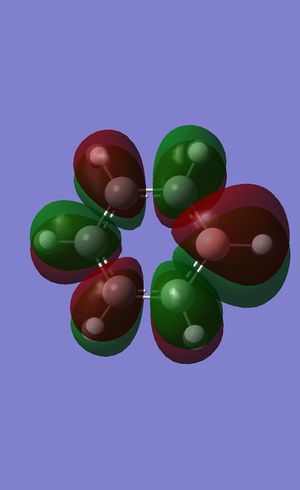
All π-bonding combination
Benzene (-0.35998 a.u.):
Boratabenzene (-0.13208 a.u.):
Pyridinium (-0.64064 a.u.):
Borazine (-0.36130 a.u.):
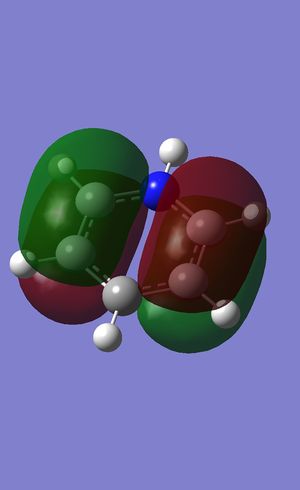
HOMO
Benzene degenerate HOMO (-0.24692, -0.24691 a.u.):
Boratabenzene (0.01094 a.u.):
Pyridinium (-0.47885):
Borazine degenerate HOMO (-0.27591, -0.27590 a.u.):
All π* antibonding combination
Benzene (0.16190 a.u.):
Boratabenzene (0.37027 a.u.):
Pyridinium (0.07317 a.u.):
Borazine (0.12496 a.u.):
Comparison
The all π-bonding orbital of benzene is completely symmetrical due to the fact that there are 6 identical carbons atoms all contributing equally to this orbital. By contrast, replacing one of the C's with a N+ or B- removes this high level of symmetry by distorting the electron cloud. As the N is more electronegative than C, its pz will contribute more to the bonding orbital than the surrounding carbons and hence there is a slightly higher electron density over the position of the ring the N resides in. By contrast, the B is less electronegative than the surrounding C's and will therefore by the same reasoning contribute less electron density from its pz to the bonding MO, leading to a slightly lower electron density in the position of the ring corresponding to the B atom. In the case of borazine, there is an even greater difference in electronegativity between the B and N than there is compared to C, but as these atoms are distributed evenly around the ring, the π cloud electron density distribution remains highly symmetrical.
Similar effects are seen in the HOMO of benzene and it's analogues, with the main difference relating to the degeneracies of the MO's. It is apparent straight away that the benzene and borazine compounds have degenerate HOMO's, whereas the pyridinium and boratabenzene derivatives do not. This is because the addition of a single heteroatom to the structure removes the symmetry of the compound and therefore the degeneracy of the HOMO level.
As expected, the opposite to what was seen for the all π-bonding MO is seen in the all π* antibonding MO's. Here, the more electronegative N's pz contributed less to this MO than the corresponding C's around the ring, whereas the more electropositive B's pz contributes more to this antibonding MO, as seen the by the respectively smaller and larger lobes over the heteroatom. Borazine is a more interesting case with the difference in electronegativity between the N and B atoms manifesting itself in the very obvious size of the lobes over the respective atoms. Here, the more electropositive B contributes much more to the MO than the more electronegative N.
In terms of energetics, the orbits with the presence of the more electronegative N atom will have a lower energy than the other analogues, with the more electropositive Boron containing Boratabenzene having the highest energy and benzene and borazine lying in the middle with very similar energies. The calculations indicate that the borazine compound has a slightly lower MO energies than the corresponding benzene analogue. This is possibly due to the increased electronegativity of the N atoms outweighing the increased electropositivity of the B atoms when compared to the all Carbon compound.
References
- ↑ "TlBr3" J.Glaser and G.Johansson; Acta Chemica Scandinavica; 1982; 36; 125-135