Rep:Mod:Laura91
Module 1: Techniques of moleuclar mechanisms and semi-emperical molecular orbital methods for structural and spectroscopic evaluations
The hydrogenation of a cyclopentadiene dimer
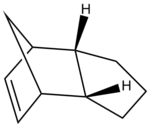
The cyclopentadiene dimer shown on the right is the exo product of the dimerisation of cyclopentadiene which occurs by a reversible diels alder mechanism typically at room temperature in a matter of hours, this is a 4+2 cycloaddition between two cyclopentadiene molecules. The cyclopentadiene dimer 1 has been created in ChemDraw and imported into ChemBio 3D, the structure has been optimised in ChemBio 3D by going to Calculations >> MM2 >> Minimise Energy >> Run this effectively corrects the structure to produce and energy minimum.
jmol for cyclopentadiene dimer 1 can be viewed here
The data obtained from the minimisation is shown below.
----------MM2 Minimization------- Note: All parameters used are finalized (Quality = 4). Iteration 107: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 1.2853 Bend: 20.5815 Stretch-Bend: -0.8383 Torsion: 7.6552 Non-1,4 VDW: -1.4180 1,4 VDW: 4.2334 Dipole/Dipole: 0.3775 Total Energy: 31.8765 kcal/mol Calculation completed ------------------------------------
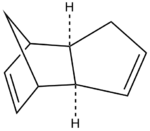
Cyclopentadiene dimer 2 has been created in ChemDraw and opened in ChemBio3D the structure has been minimised and corrected using the MM2 calculation compariive to cyclopentadiene dimer 1. The data obtained for this minimisation is shown below and the strucutre used for this caclulation is shown on the right, this is the endo product from the diels alder reaction of cyclopentadiene with another cyclopentadiene molecule.
jmol for cyclopentadiene dimer 2 can be viewed here
------------MM2 Minimization------------ Note: All parameters used are finalized (Quality = 4). Iteration 81: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 1.2506 Bend: 20.8458 Stretch-Bend: -0.8355 Torsion: 9.5109 Non-1,4 VDW: -1.5416 1,4 VDW: 4.3198 Dipole/Dipole: 0.4475 Total Energy: 33.9975 kcal/mol Calculation completed ------------------------------------
| Molecule | Stretch | Bend | Stretch-Bend | Torsion | Non-1,4 VDW | 1,4 VDW | Dipole-Dipole | Total Energies MM2 (kcal/mol) |
| 1 | 1.29 | 20.58 | -0.84 | 7.65 | -1.42 | 4.23 | 0.38 | 31.88 |
| 2 | 1.25 | 20.85 | -0.84 | 9.51 | -1.54 | 4.32 | 0.45 | 34.00 |
The diels alder reaction selectively occurs producing the endo-dimer 2, when this dimer is hydrogenated it leads to the selective product corresponding to the structure of either 3 or 4 shown below, these structures are dihydro derivatives. However it has been shown that upon prolonged hydrogenation the tetrahydro derivative is predominately formed. Using the MM2 calculation previously used on structures 1 and 2 above, the relative energies, dipole/dipole, Van der Waals, torsional strain, stretch and bending energies can all be calculated for structures 3 and 4. The comparison of this data leads to the important conclusion regarding the pairs of structures 1/2 and 3/4, showing which pair is thermodynamicaly more stable regarding steric hinderence and strain.
Comparison of the data obtained from structures 1 and 2, the final product for the endo structure is higher in energy compared to the exo structure 2. The difference in the energy between the endo and exo isomer is approximation 2.1kcal/mol from the MM2 calcualtion, this increased stability suggests that dimer 1 is more thermodyanmically stable. The endo isomer is destabilized by a 1,4 allylic interaction which isn't present in the exo isomer. The endo isomer is less thermodynamicall favorable but this conformation is still favoured as the endo isomer must have a lower transition state during the diels alder reaction, by being a kinetic stability as the product would be formed faster for 2 compared to 1. Using the Woodward and Hoffmann [1] theory it can be predicted that the endo transition state conformation allows better orbital overlap of occupied and unoccupied orbitals by having a better orbital symmetry and therefore overlap compared to the exo transition state, in the diels alder reaction the HOMO-LUMO interaction is extremly important and a good overlap of these orbitals is required. The energies obtained for the two structures for stretching, bending and stretch-bend are very similar and therefore these don't play the key role in favouring either prodcut during the reaction. The Aldo [2] rule states that the endo isomer is less thermodynamically stable due to being more sterically crowed and consequently having a higher torsional strain. The torsional energy is hihger for the endo product this is due to slightly more strain present in the conformation, the VDW energies are very similar for both structures along side the Dipole/Dipople energies and therefore these don't contribute to the favouring of the endo product. Molecular modeling cannot prove that the transition state for structure 2 is lower in energy as the basic principles used to work out calculations are based on fixed atoms which vibrate analogus to a mass on a string in classical terms. To consider the energies of the transition states quantum mechanics needs to be introduced using a basis set like DFT and the calculation can be run in gaussian. When quantum mechanics are used in a modeling calculation the basis set uses the overall electron distribution of a molecule, therefore bonds can effectively be broken and made to figure out energies and molecular orbitals thus a transition state energy can be determined.
Below is the MM2 calculation using the setup described previosuly, the calculation was completed on structure 3 shown to the right.
jmol for dihydroderivative 3 can be viewed here
------------MM2 Minimization------------ Note: All parameters used are finalized (Quality = 4). Iteration 2: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 1.2356 Bend: 18.9358 Stretch-Bend: -0.7611 Torsion: 12.1246 Non-1,4 VDW: -1.5007 1,4 VDW: 5.7294 Dipole/Dipole: 0.1631 Total Energy: 35.9266 kcal/mol Calculation completed ------------------------------------
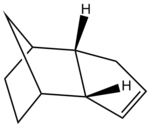
Below is the MM2 calculation data using the setup described previosuly, the calculation was completed on structure 4 shown to the right.
jmol for dihydroderivative 4 can be viewed here
------------MM2 Minimization------------ Note: All parameters used are finalized (Quality = 4). Iteration 152: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 1.0969 Bend: 14.5251 Stretch-Bend: -0.5495 Torsion: 12.4979 Non-1,4 VDW: -1.0706 1,4 VDW: 4.5117 Dipole/Dipole: 0.1406 Total Energy: 31.1520 kcal/mol Calculation completed ---------------------------------------
| Molecule | Stretch | Bend | Stretch-Bend | Torsion | Non-1,4 VDW | 1,4 VDW | Dipole-Dipole | Total Energies MM2 (kcal/mol) |
| 3 | 1.24 | 18.94 | -0.76 | 12.2 | -1.50 | 5.73 | 0.16 | 35.93 |
| 4 | 1.10 | 14.53 | -0.55 | 12.50 | -1.67 | 4.51 | 0.24 | 31.15 |
Upon hydrogenation of the endo isomer (structure 2) either structure 3 or 4 can be the product. Structure 4 has a lower total energy, due to a lower bend energy whcih is the amount of energy the triatomic bond angle is from ideality. In some cases the thermodynamic product might also be the kinetic product. The hydrogenation reaction is irreversible therefore kinetic prodcuts and thermodynamic products can't be applied. These MM2 calculationsa can't be used to determine the prodcut that will predominatly be formed during the hydrogenation reactions. The product that has the lowest total energy may also have the lowest transition state barrier but to find this information out complex quantum mechanics in needed, as stated above the DFT basis set could be used.
Taxol is a chemotherapy drug and the key intermediate in the synthesis is thought to be either of the structure's 9 or 10, theses structures a formed as a result of an Oxy-cope of a previous derivative [3]. Upon standing the compound isomerises by a type of isomerism known as atropisomerism [4]. This type of isomerisim is a result of a hindered rotation about a single bond however the steric strain barrier to rotation is extremely high as expected and this then allows the resulting isolation of the conformers [5]. From this one can induce that one isomer is more thermodynamicaly stable and therefore forms upon standing, and the synthesized isomer is the kinetic product. In this next section I will explore which of the two atropisomers is more stable. This will be done by using the MM2 force field calculation and a comparison to the MMFF94 field procedure will be made. The structure's have been created in ChemDraw and imported into ChemBio 3D, the structure has been optimized in ChemBio 3D by going to Calculations >> MM2 >> Minimise Energy >> Run this effectively corrects the structure to produce and energy minimum. Then a comparison to this calculation has been made by going to Calculations >> MMFF94 >> Minimize Energy >> Run. The structures have been manually manipulated to produce the best optimised geometry after running the calculation.
jmol for cyclopentadiene taxol intermediate 10 can be viewed here
The minimization data for the MM2 calculation of taxol intermediate 10 is shown below.
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 353: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.5502 Bend: 11.3747 Stretch-Bend: 0.3199 Torsion: 17.3634 Non-1,4 VDW: -2.2623 1,4 VDW: 12.7438 Dipole/Dipole: -1.6996 Total Energy: 40.3901 kcal/mol Calculation completed -----------------------------------------
The minimisation data for the MMFF94 calculation on taxol intermediate 10 is shown below.
------------MMFF94 Minimization------------ Iteration 70: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Final Energy: 60.6482 kcal/mol Calculation completed -------------------------------------------
jmol for taxol intermediate 9 can be viewed here
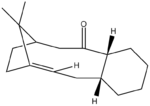
The minimisation for the taxol intermediate 9 is shown below using the MM2 model.
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 239: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.6190 Bend: 11.3443 Stretch-Bend: 0.3431 Torsion: 19.6652 Non-1,4 VDW: -2.1592 1,4 VDW: 12.8730 Dipole/Dipole: -2.0024 Total Energy: 42.6829 kcal/mol Calculation completed ------------------------------------
The calculation was repeated using the MMFF94 model on taxol intermediate 9, the data obtained is shown below.
------------MMFF94 Minimization------------ Iteration 37: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Final Energy: 60.562 kcal/mol Calculation completed ------------------------------------
| Molecule | Stretch | Bend | Stretch-Bend | Torsion | Non-1,4 VDW | 1,4 VDW | Dipole-Dipole | Total Energies MM2 (kcal/mol) | Total Energies MMFF94 (kcal/mol) |
| Taxol 10 | 2.55 | 11.37 | 0.32 | 17.36 | -2.26 | 12.74 | -1.70 | 40.4 | 60.648 |
| Taxol 9 | 2.62 | 11.34 | 0.34 | 19.67 | -2.16 | 12.87 | -2.00 | 42.7 | 60.562 |
Olefins at bridgehead positions are normally unfavourable due to the increase in steric strain on the system, however an increase in cyclic ring size can actually favour the alkene bond at this bridgehead position [6]. It is important to note that Bredt observed this chemistry and came up with Bredt's [6] rule which states that a double bond can't be placed at a bridgehead position of a ringed system, but this rule may be violated is the ring is big enough and the structure is stable these types of molecules are known as anti-Bredt [6] systems. Hyperstable alkenes have been shown to have negative alkene energies, in other words the strain energy of the alkene is much lower than that of the corresponding hydrocarbon [7]. Literature has shown that the negative strain energy of a hyperstable alkene at a bridgehead has an impact on the heats of hydrogenation, making the values far lower than expected, the lower this value is the more stable the alkene is towards hydrogenation thermodynamically and therefore hydrogenation proceeds much slower than expected [7]. The calculations above have been carried out using empirical force field parameters which can only give information regarding thermodynamic stability of the ground state structure, it is important to note that chemical reactivity is directly related to transition state energies and the energy difference between the ground state and the transition state structures which the MM2 calculation cannot provide information on. Form the data obtained above the Taxol 10 intermediate appears to be more stable with a lower total energy of the system by ~2.3kcal/mol, the main contribution to this energy is the olefin and the secondary contribution comes from the skeletal carbon frame work of the ring system and that of the strained bridgehead [7]. The MMFF94 calculation produces similar results for both taxol 9 and 10 structures, however the energies obtained from this calculation cannot be compared to the energies obtained from the MM2 calculation as there is a difference in the geomoteries of the two structure's [8]. The more stable isomer is taxol 10 which is likely to be the thermodynamic product and therefore more likely to form upon standing of the reaction mixture,this means that taxol intermediate isomer 9 is more likely to be the kinetic product initially formed during the synthesis.
Regioselective addition of Dichlorocarbene to a diene
In this next section quantum mechanics is introduced to obtain the molecular orbital distribution fo compound 12 shown on the right, quantum mechanics is used to account for the wave-like behavour that an electron experiences from the wave-particle duality theory [9]. The molecular moodeling previously used cannot be used for this, the electron distribution wil be investigated and related to bonding and spectroscopic analysis. Compound 12 can react with electrophilic reagents which are electron acceptors examples of such compound include peracids [10] and carbenes[10] . To predict reactivity the optimised geometry is needed this can be calculated using molecular modeling mechanics, the second piece of information needed are the molecular orbitals which can be displayed graphically in gaussview or ChemBio3D. This section will explore the electronic interactions present in molecule 12 and this information can then be analysed to give information regarding the geometry and reactivity of molecule 12.
Molecular mechanics calculation has been run in ChemBio3D, the molecule was created in ChemDraw and loaded into ChemBio3D. The calculation has been set up by going to Calculations >> MM2 >> Minimise Energy >> Run this effectively corrects the structure to produce an energy minimum.
jmol for compound 12 can be viewed here
The data obtained from the MM2 optimisation is show below.
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 147: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 0.6195 Bend: 4.7370 Stretch-Bend: 0.0401 Torsion: 7.6591 Non-1,4 VDW: -1.0672 1,4 VDW: 5.7937 Dipole/Dipole: 0.1123 Total Energy: 17.8945 kcal/mol Calculation completed ------------------------------------
This calculation was then repeated using Calculations >> MOPAC Interface >> Minimise Energy and under Job and Theory the method selected was RM1. The results folder was changed to the desktop if this is not completed an error message occurs. After clicking Run the calculation completed very quickly.
The results obtained from the MOPAC calculation.
FINAL HEAT OF FORMATION = 22.82754 KCAL = 95.51044 KJ
TOTAL ENERGY = -1945.65405 EV
ELECTRONIC ENERGY = -11247.51961 EV POINT GROUP: Cs
CORE-CORE REPULSION = 9301.86556 EV
COSMO AREA = 195.09 SQUARE ANGSTROMS
COSMO VOLUME = 214.23 CUBIC ANGSTROMS
IONIZATION POTENTIAL = 9.112825 EV
HOMO LUMO ENERGIES (EV) = -9.113 1.069
NO. OF FILLED LEVELS = 32
MOLECULAR WEIGHT = 180.677
From these calculations the optimised structure can be compared between the two molecular modeling methods, this is done my overlaying the molecules. The MM2 and MOPAC calculations have been completed in seperate window. The overlay is done by selecting all and copying and pasting one molecule into the other window, in one window there is now the two molecules side by side each other. After this paris of atoms can be selected between the two molecules by using the select button and selecting the first atom and then the second by shift-click. After a pair of atoms have been selected the distance is measured between these pairs this is done by using structure>measurements>display distance measurements. This method has been repeated to obtain four pairs with the measured distance. Once this is completed the overlay can be optimised inorder to compare the geometry, this is done by going to structure>overlay>minimise>start This is repeated until the distance between the four pairs is minimised, if the molecules are identical in structure the minimisation will be reduced to zero). A screen snap of the overlay has been shown below.
jmol for compound 12 overlay can be viewed here
From this screen snap it shows the structures don't perfectly overlay one-another as all the bonds after optimisation don't turn to 0Å, two of the bonds are 0Å and at this point the strucutres are identical to each other. Although the deviations are only small between some bonds being 0.1Å this still shows that the strucutres are not identical to each other. It is important to note that some bonds deviate more than others in the molecule and the deviations are depenedent on the pairs of atoms that are selected. Deviation is expected between these structures as a different optimisation model has been used on each structure, only structures which use the same optimsation model can be compared. The MOPAC calculation includes the stereoelectronic effects in the molecule, the MOPAC calculation has produced a higher energy being 23kcal/mol compared to the MM2 calculation producing a total energy of 18kcal/mol.
The molecular orbitals can now be computed and two different methods can be analysed for this procedure, the HOMO is of the greatest interest during this calculations this is because the HOMO controls the reactivity towards the approaching electrophile.
The moleuclar orbitals have been calculated by going to calculations>gaussian interface>use advance mode the input file was then edited by changing the four lines to read:
1.%Chk=[JobTititle].chk 2.%nprocshared=4 3.%Mem=1GB 4.# B3LYP/6-31G Test
The results folder was changed to the desktop otherwise an error occurs, the calculation was then left to run. After the calculation has completed the molecular orbitals were invoked by going to surfaces>molecular orbitals other orbitals can be selecteded by going to surfaces>select molecular orbitals. The molecular orbital surfaces has been adjusted by going to surfaces>isocontour and then surfaces>display>translucent.
 |
 |
 |
 |
 |
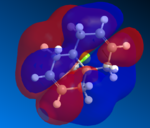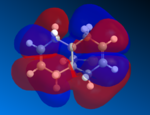| N=31 E=-10.901 eV | N=32 E=-10.387 eV | N=33 E=0.966 eV | N=34 E=1.404 eV | N=35 E=15.116 eV |
The two alkene bonds are not discriminated against, this is because there is psuedo-symmetry [11] of Cs type shown in the diagram to the the right, this symmetry is reflected in the molecular oribtals, in other words the symmetry along A1 accounts for the C=C orbital distribution being symmetrical and non discriminating between the two alkene, therefore the electron density is the same using this basis set. The A2 symmetry accounts for the individual carbon atoms reflecting the same orbital symmetry to one another. The symmetry of the molecular orbitals is extremly important along with shape and orbital energy.
The molecular electrostatic potential (MEP) can now be analysed using the MOPAC geometery by going to surface>Choose Surface>Molecular electrostatic potential and changing the surface>isopotential to a maximum which will now differentiation between the two alkenes. The MEP shows the total electron distribution in the molecule by putting together an overall picture of all molecular orbitals electron density. Once again the two alkenes are not discriminated against using this basis set due to the pseudo Cs type symmetry, using pseudo symmetry leads to an inaccurate representation of the molecule, the Cl electronic properties and influence aren't concidered. The MEP has an attractive and repulsive surface, an area that is attractive is generally electropositive, therefore electron poor in nature this is demonstrated by the blue colour in the MEP below, in contrast to this a repulsive surface indicates and area of high electron density and an electronegative region this is shown below by the red colour. The chlorine atom is electronegative, as it is electron rich and is therefore red in colour around the PES. The MEP is shown below for molecule 12.
jmol for compound 12 MEP can be viewed here
The C=C molecular vibrations can now be analysed for molecule 12, the most important vibrations are the C=C and the C-Cl, paying particular attention to the influence of vibrations from the C-Cl bond. The method that has been used is the density functional approach ; the optimised geometry for molecule 12 has been used. The vibrations were calculated by going to calculations>Gaussian Interface>Create input file, the input file was then saved to the desktop and opened in NotePad++ to edit the document. The top line of the text document was made to read "# b31lyp/6-31G(d,p) opt freq", the calculation was then submitted to the HPC service SCAN chem lab 1. DOI link to the files is found here: DOI:10042/24126
The calculation has converged shown in the table below and therefore has been successful.
Maximum Force 0.000036 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000449 0.001800 YES RMS Displacement 0.000114 0.001200 YES
Below are the low frequencies which are all between ±15cm-1 as expected which also shows that the calculation has been successful.
Low frequencies --- -5.4989 -0.0025 0.0007 0.0014 7.5192 10.6326 Low frequencies --- 90.2534 125.6211 158.1301
The table below shows the frequency stretches which are present in molecule 12, only the vibrations with large intensities have been shown, click on the image to view the vibration.
| Vibrational Mode | Vibrational Motion | Frequency (Cm-1) | Intensity | |||
| 18 |  |
689 | 53 | |||
| 19 |  |
771 | 25 | |||
| 44 |  |
1361 | 10 | |||
| 55 |  |
1737 | 4 | |||
| 56 |  |
1757 | 4 | |||
| 57 |  |
3000 | 11 | |||
| 58 |  |
3000 | 20 | |||
| 59 |  |
3010 | 101 | |||
| 61 |  |
3029 | 23 | |||
| 63 |  |
3034 | 63 | |||
| 67 |  |
3176 | 55 | |||
| 68 |  |
3179 | 35 | |||
Typical C=C stretches occur approximetly between 1690-1620cm-1 while the =CH stretch in alkenes occurs approximetly between 3110-3010cm-1. The C=C stretches for diene molecule 12 have been identified above as 1737 and 1757cm-1 these frequencies refer to the endo double bond with respect to the chlorine atom and the exo double bond with respect to the chlorine atom respectively. It is important to note that the the diene C=C stretches are much lower than the typical alkene stretches previously mentioned, this is due to electronic effect of the chlorine atom. Electron density from the sigma Cl-C bond is donated into the C=C pi* orbital, the added electron density into the pi* orbital weakends the C=C bond, this is reflected by the decrease in the vibrational frequency. This method has discriminated this time against the two alkene bonds therefore producing different vibrational frequencies, by taking into account of the additional electron density donated from the chlorine atom to one alkene, which contrasts with the MO calculation. The pseudo symmetry has been disregarded in this calculation.
Monosaccharide Chemistry and the mechanism of glycosidation
The glycosidation mechanisms is shown below, by which an incomming nucleophile replaces group X, this type of mechanism is very stereospecific, wherby the stereochemistry is controlled by the C-OAc bond. It is thought that the mecahnism is majorly controlled by neighbouring group effects of the acetyl group, the mechanism goes through two intermediated A and B. The neighbouring group participation plays an important role in the destabalisation/stabilisation of intermediate A which will be explored further in this section, a second intermedaite B an oxenium cation is generated which is followed with the attack of the nucleophile occuring from either the top or bottom face to produce the final product, this section will also explore this possibility.
The intermedate A has been created in ChemDraw and opened in ChemBio, two calculatons have been completed on the 4 anomers of intermediate A, with all four structures being shown below. The first calculation has been set up by going to Calculations >> MM2 >> Minimise Energy >> Run, followed by the second calculation which was set up by going to Calculations >> MOPAC Interface >> Minimise Energy and under Job and Theory the method selected was PM6. The mechanism is shown below.
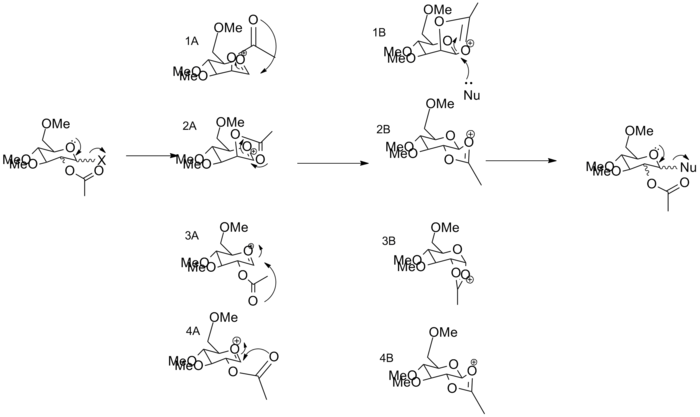
A1 intermediate A is shown above, in this structure both the C-OAc bond is up and the acetyl group is above the plain of the ring.
MM2 calculation is shown below for this structure.
jmol for anomer 1 of intermediate A can be viewed here
------------MM2 Minimization------------ Separating coincident atoms: Lp(40)-Lp(41) Warning: Some parameters are guessed (Quality = 1). Iteration 500: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.7629 Bend: 11.0671 Stretch-Bend: 1.0312 Torsion: 1.9660 Non-1,4 VDW: 1.7250 1,4 VDW: 18.6086 Charge/Dipole: -24.1698 Dipole/Dipole: 6.4829 Total Energy: 19.4738 kcal/mol Calculation completed ------------------------------------
MOPAC calculation data is shown below for structure 1.
FINAL HEAT OF FORMATION = -91.65047 KCAL = -383.46557 KJ
TOTAL ENERGY = -3347.58687 EV
ELECTRONIC ENERGY = -22795.26862 EV POINT GROUP: C1
CORE-CORE REPULSION = 19447.68175 EV
COSMO AREA = 263.26 SQUARE ANGSTROMS
COSMO VOLUME = 299.33 CUBIC ANGSTROMS
IONIZATION POTENTIAL = 12.952734 EV
HOMO LUMO ENERGIES (EV) = -12.953 -4.742
NO. OF FILLED LEVELS = 49
MOLECULAR WEIGHT = 247.268
MOLECULAR DIMENSIONS (Angstroms)
Atom Atom Distance
H 27 H 34 9.39302
H 31 H 28 6.88565
H 29 H 21 5.32347
SCF CALCULATIONS = 280
COMPUTATION TIME = 10.062 SECONDS
A2 in this structure the C-OAc bond is up and the acetyl group is below the plain of the ring.
jmol for anomer 2 of intermediate A can be viewed here
MM2 calculation is shown below for this structure.
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 593: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.4870 Bend: 9.9560 Stretch-Bend: 0.8402 Torsion: 1.7468 Non-1,4 VDW: -1.0047 1,4 VDW: 19.0815 Charge/Dipole: -9.9460 Dipole/Dipole: 4.1803 Total Energy: 27.3411 kcal/mol Calculation completed ------------------------------------
Below is the MOPAC calculation for intermediate 2
FINAL HEAT OF FORMATION = -88.54545 KCAL = -370.47415 KJ
TOTAL ENERGY = -3347.45222 EV
ELECTRONIC ENERGY = -22942.34176 EV POINT GROUP: C1
CORE-CORE REPULSION = 19594.88954 EV
COSMO AREA = 259.32 SQUARE ANGSTROMS
COSMO VOLUME = 297.87 CUBIC ANGSTROMS
IONIZATION POTENTIAL = 13.027825 EV
HOMO LUMO ENERGIES (EV) = -13.028 -4.763
NO. OF FILLED LEVELS = 49
MOLECULAR WEIGHT = 247.268
MOLECULAR DIMENSIONS (Angstroms)
Atom Atom Distance
H 27 H 34 8.97953
H 31 H 26 6.81333
H 21 H 28 6.00473
SCF CALCULATIONS = 288
COMPUTATION TIME = 10.093 SECONDS
A3 of intermediate A, in this structure both the C-OAc bond is down and the acetyl group is below the plain of the ring.
jmol for anomer 1 of intermediate A can be viewed here
MM2 calculation is shown below for this structure.
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 454: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.6960 Bend: 9.9838 Stretch-Bend: 0.9350 Torsion: 2.9302 Non-1,4 VDW: 0.0599 1,4 VDW: 19.3927 Charge/Dipole: -21.6348 Dipole/Dipole: 5.8944 Total Energy: 20.2572 kcal/mol Calculation completed ------------------------------------
MOPAC calculation for anomer 3 using the basis set PM6.
FINAL HEAT OF FORMATION = -88.73042 KCAL = -371.24808 KJ
TOTAL ENERGY = -3347.46024 EV
ELECTRONIC ENERGY = -23054.86106 EV POINT GROUP: C1
CORE-CORE REPULSION = 19707.40082 EV
COSMO AREA = 255.85 SQUARE ANGSTROMS
COSMO VOLUME = 293.63 CUBIC ANGSTROMS
IONIZATION POTENTIAL = 13.142684 EV
HOMO LUMO ENERGIES (EV) = -13.143 -4.751
NO. OF FILLED LEVELS = 49
MOLECULAR WEIGHT = 247.268
MOLECULAR DIMENSIONS (Angstroms)
Atom Atom Distance
H 27 H 34 8.82913
H 31 H 26 6.82180
H 21 H 28 5.79588
SCF CALCULATIONS = 335
COMPUTATION TIME = 12.730 SECONDS
A4 of intermediate A, in this structure the C-OAc bond is down and the acetyl group is above the plain of the ring.
jmol for anomer 4 of intermediate A can be viewed here
MM2 calculation is shown below for this structure.
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 691: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 2.5236 Bend: 9.4286 Stretch-Bend: 0.8935 Torsion: 3.9884 Non-1,4 VDW: -1.9031 1,4 VDW: 19.8115 Charge/Dipole: -8.3205 Dipole/Dipole: 4.6516 Total Energy: 31.0736 kcal/mol Calculation completed ------------------------------------
MOPAC PM6 calculation shown below.
FINAL HEAT OF FORMATION = -76.88889 KCAL = -321.70311 KJ
TOTAL ENERGY = -3346.94675 EV
ELECTRONIC ENERGY = -22049.17203 EV POINT GROUP: C1
CORE-CORE REPULSION = 18702.22529 EV
COSMO AREA = 271.54 SQUARE ANGSTROMS
COSMO VOLUME = 299.84 CUBIC ANGSTROMS
IONIZATION POTENTIAL = 13.431726 EV
HOMO LUMO ENERGIES (EV) = -13.432 -5.784
NO. OF FILLED LEVELS = 49
MOLECULAR WEIGHT = 247.268
MOLECULAR DIMENSIONS (Angstroms)
Atom Atom Distance
H 34 H 25 10.91082
H 30 H 31 7.10548
H 21 H 29 5.27285
SCF CALCULATIONS = 317
COMPUTATION TIME = 11.934 SECONDS
| Molecule | Stretch | Bend | Stretch-Bend | Torsion | Non-1,4 VDW | 1,4 VDW | Charge-Dipole | Dipole-Dipole | Total Energies MM2 (kcal/mol) | Heat of formation MOPAC (kcal/mol) |
| 1A | 2.76 | 11.07 | 1.03 | 1.97 | 1.73 | 18.61 | -24.17 | 6.48 | 19.47 | -91.65 |
| 2A | 2.49 | 9.96 | 0.84 | 1.75 | -1.0 | 19.08 | -9.95 | 4.18 | 27.34 | -88.55 |
| 3A | 2.70 | 9.98 | 0.94 | 2.93 | 0.06 | 19.39 | -21.63 | 5.89 | 20.26 | -88.73 |
| 4A | 2.52 | 9.43 | 0.89 | 3.99 | -1.9 | 19.81 | -8.32 | 4.65 | 37.07 | -76.89 |
From this table it is apparent that the lower energy isomers are 1A and 3A.
The four isomers of structure B as shown in the mechanism above have been investigated, below is a table showing the data obtained.
| Molecule | Stretch | Bend | Stretch-Bend | Torsion | Non-1,4 VDW | 1,4 VDW | Charge-Dipole | Dipole-Dipole | Total Energies MM2 (kcal/mol) | MOPAC PM6 (kcal/mol) |
| 1B | 1.9334 | 13.1983 | 0.6603 | 7.1039 | -2.6042 | 17.9657 | -10.4214 | 0.0681 | 27.9040 | -88.22009 |
| 2B | 1.9493 | 13.7969 | 0.6920 | 7.5714 | -3.7567 | 18.0544 | 4.2395 | -1.9023 | 40.6445 | -66.72478 |
| 3B | 2.0338 | 12.4001 | 0.6699 | 10.6033 | -4.0276 | 18.9272 | -6.9551 | -0.6274 | 33.0243 | -88.54610 |
| 4B | 2.7330 | 17.3228 | 0.7909 | 8.2158 | -2.6200 | 19.3405 | 2.0562 | -1.7295 | 46.1096 | -66.84161 |
It is important to note that the MOPAC calculation has been included to account for the lone pair effects on the oxygen and also the oxonium cation both of which aren't included in the MM2 calculation. It is apparent from this data that the A1/B1 isomers and the A3/B3 structures are lowest in energy, the former being the lowest in energy. The difference in energy and therefore stability can be related to the attack of the carbonyl atom relative to the carbon [12]. The trans 5,6 is preffered to a cis 5,6 conformation due to the increased stability this increased the stability of the attacking carbonyl geometry allowing the carbonyl to be trans to the respective acetyl group [12]. The ideal angle for attack is 107•C also know as the Burger-Dunitz angle [13], and it can be seen from the bond angle above that there is large deviation from this angle.
References Section 1
- ↑ R. B. Woodward, Roald Hoffmann J. Am. Chem. Soc.; 1965; 87(2); 395-397. DOI:10.1021/ja01080a054
- ↑ Masahiro Imade, Hajime Hirao, Kiyoyuki Omoto, and Hiroshi Fujimoto*J. Org. Chem. 1999, 64, 6697-6701
- ↑ S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, 319; DOI:10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0
- ↑ See J. G. Vinter and H. M. R. Hoffman, J. Am. Chem. Soc., 1974, 96, 5466 (DOI:10.1021/ja00824a025 DOI:10.1021/ja00824a025 ) and 95, 3051 for another nice example of atropisomerism.
- ↑ Bringmann G, Mortimer AJP, Keller PA, Gresser MJ, Garner J, Breuning M (2005). "Atroposelective Synthesis of Axially Chiral Biaryl Compounds". Angewandte Chemie International Edition 44 (34): 5384–5427. doi:10.1002/anie.200462661.
- ↑ 6.0 6.1 6.2 McEwen and Schleyer, J. Am. Chem. SOC., Vol. 108, No. 14, 1986, 3952
- ↑ 7.0 7.1 7.2 J . Alan B. McEwent and Paul von Rag& Schleyer, Am. Chem. SOC. 1986, 108, 3951-3960
- ↑ Arthur Greenberg,* David T. Moore, and Thomas D. DuBois, J. Am. Chem. Soc. 1996, 118, 8658-8668.
- ↑ Walter Greiner (2001). Quantum Mechanics: An Introduction. Springer.
- ↑ 10.0 10.1 B. Halton, R. Boese and H. S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447. DOI:10.1039/P29920000447
- ↑ David Casanova, Pere Alemany, Andres Falceto,Abel Carreras, and Santiago Alvarez, Journal of Computational Chemistry 2013, 000, 000–000. DOI:10.1002/jcc.23257
- ↑ 12.0 12.1 Dennis M. Whitfielda, Tomoo Nukadab, Carbohydrate Research, Volume 342, Issue 10, 23 July 2007, Pages 1291–1304.
- ↑ H. B. Bürgi, J. D. Dunitz, J. M. Lehn, G. Wipff (1974). "Stereochemistry of reaction paths at carbonyl centres". Tetrahedron 30 (12): 1563–1572. Error: Bad DOI specified!
Module 1 Mini-Project: Stimulation of spectroscopic data for a literature molecule
Synthetic chemistry procedures often give a mixture of products, which may be isomers. Some reaction products which are solids can be crystalised and the structures can then be analysed by X-ray crystallography. When a compound is an oil or liquid this method cannot be used to determine the structure and to chracterise the structure spectroscopic methods are used. Some of these spectroscopic methods include: Mass spectroscopy, NMR spectroscopy, UV-Vis and IR. Although these techniques are available they don't all differentiate between different isomers. Computational analysis of a compound can be used to predict the spectroscopic properties.
Molecule 17 shown on the right has been created in ChemDraw and imported into ChemBio3D, here the MM2 calculation has been carried out to minimize the geometry, the data obtained is shown below.
jmol for molecule 17 can be viewed here
------------MM2 Minimization------------ Warning: Some parameters are guessed (Quality = 1). Iteration 687: Minimization terminated normally because the gradient norm is less than the minimum gradient norm Stretch: 4.8463 Bend: 20.9249 Stretch-Bend: 0.7139 Torsion: 23.1420 Non-1,4 VDW: -0.5470 1,4 VDW: 18.4590 Dipole/Dipole: -2.4161 Total Energy: 65.1230 kcal/mol Calculation completed ------------------------------------
The next stage requires the geometry to be calculated at the density functional level (DFT), this is done by going to calculations>gaussian interface>create input file. The parameters used were: job type as minimum,method as DFT, B3LYP, basis set as 6-31G(d,p) and solvation as CPCM solvent chloroform. The job was submitted to the scan service and the DOI link can be found here:DOI:10042/24229
The fchk file has been downloaded and saved as new input file for the NMR calculation, the document was edited by changing the first line in the text document to # mpw1pw91/6-31G(d,p) NMR SCRF=(CPCM, Solvent=chloroform) the document was then submitted to the scan service. The DOI link can be accessed here, DOI:10042/24281
The results were opened by going to Results/NMR
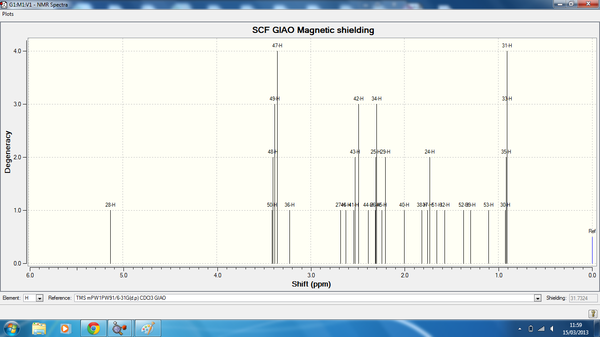
Taxol_der_HNMR.png
| Atom | Degeneracy | Calculated chemical shift (ppm) | Literature Chemical Shift [1] (ppm) |
| 28 | 1 | 4.93 | 5.21 |
| 50 | 3 | 3.21 | 3.00-2.70 |
| 48 | 4 | 3.20 | 3.00-2.70 |
| 49 | 4 | 3.18 | 3.00-2.70 |
| 47 | 4 | 3.15 | 3.00-2.70 |
| 36 | 1 | 3.02 | 3.00-2.70 |
| 27 | 1 | 2.48 | 2.70-2.35 |
| 46 | 1 | 2.42 | 2.70-2.35 |
| 41 | 3 | 2.34 | 2.70-2.35 |
| 43 | 3 | 2.33 | 2.70-2.35 |
| 42 | 3 | 2.29 | 2.20-1.70 |
| 44 | 1 | 2.19 | 2.20-1.70 |
| 26 | 3 | 2.11 | 2.20-1.70 |
| 25 | 3 | 2.11 | 2.20-1.70 |
| 34 | 3 | 2.10 | 2.20-1.70 |
| 45 | 2 | 2.04 | 2.20-1.70 |
| 29 | 2 | 2.01 | 2.20-1.70 |
| 40 | 1 | 1.80 | 2.20-1.70 |
| 38 | 1 | 1.62 | 1.58 |
| 37 | 2 | 1.56 | 1.50-1.20 |
| 24 | 2 | 1.53 | 1.50-1.20 |
| 51 | 1 | 1.46 | 1.50-1.20 |
| 32 | 1 | 1.37 | 1.50-1.20 |
| 52 | 1 | 1.17 | 1.50-1.20 |
| 39 | 1 | 1.10 | 1.10 |
| 53 | 1 | 0.91 | 1.07 |
| 30 | 4 | 0.73 | 1.03 |
| 35 | 4 | 0.72 | 1.03 |
| 33 | 4 | 0.71 | 1.03 |
| 31 | 4 | 0.71 | 1.03 |
The table below shows the 13CNMR spectrum generated from molecule 17.
| Atom | Degeneracy | Calculated chemical shift (ppm) | Literature Chemical Shift (ppm) |
| 9 | 1 | 217.23 | 211.49 |
| 3 | 1 | 144.04 | 148.72 |
| 4 | 1 | 119.79 | 120.90 |
| 17 | 1 | 84.61 | 74.61 |
| 10 | 4 | 62.66 | 60.53 |
| 11 | 1 | 54.17 | 51.30 |
| 5 | 1 | 50.99 | 50.94 |
| 6 | 1 | 48.37 | 45.53 |
| 14 | 1 | 45.61 | 43.28 |
| 21 | 1 | 41.85 | 40.82 |
| 22 | 1 | 41.00 | 38.73 |
| 15 | 1 | 35.79 | 36.78 |
| 18 | 1 | 32.531 | 35.47 |
| 13 | 1 | 32.04 | 30.84 |
| 1 | 1 | 28.23 | 30.00 |
| 2 | 1 | 25.00 | 25.56 |
| 7 | 1 | 23.80 | 25.35 |
| 12 | 1 | 18.85 | 22.21 |
| 8 | 1 | 17.36 | 21.39 |
| 23 | 1 | 15.93 | 19.83 |
These tables show that the predicted NMR spectra correspond well with literature, the deviations come from experimental purity of the literature compound, the difference in the optimized geometry with the species that exists in the literature, the solvent system can also effect the NMR data it is important to note that the literature uses duterated benzene also.
Literature Molecule
The next section will investigate the difference between four isomers of cocaine, the reaction scheme below details the mechanism for synthesis of cocaine. Forensic chemists have spectroscopic tools to differentiate between isomers of cocaine,and have previously used these methods to stand up in court [2]. Experimental methods including NMR, IR and MS can be used to determine the in-equivalent diastereoisomers in a racemic mixture. The enantiomeric forms of cocaine are differentiated by crystals tests, optical rotations, melting temperatures and IR [3], the diastereoisomers are allococaine [3] and pseudoallococaine [3] it is important to note that IR, NMR and MS can't be used as a method to differentiate between these enantiomers [3]. However, the diastereoisomers show significant differences in there 1HNMR spectrum regarding the C3 proton and the chemical shift associated with this environment, also both the C2 and C4 protons show a coupling pattern with the C3 protons and this coupling can also differentiate between diasteroisomers [3]The Karplus equation can be used to relate the 3J coupling constants to the change in torsional angle during NMR spectroscopy, this relationship is given by the equation [4]:
J(Φ)= Acos2Ф + BcosФ + C
A, B and C are derived parameters but are dependent on the atom type and substituents on these atoms, J is the 3J coupling constants, while Ф is the dihedral angle. [5].
Cocaine needs to be differentiated being one of eight possible structures as each diastereomers there are two enatiomers, there aren't many tests that can differentiate between all these molecules and I will attempt to investigate and solve this problem firstly by analyzing the IR and NMR data and secondly by circular dichroism. Cocaine total synthesis is shown below. [5]
jmol for cocaine isomer 1 can be viewed here jmol for cocaine isomer 2 can be viewed here jmol for cocaine isomer 3 can be viewed here jmol for cocaine isomer 4 can be viewed here
The isomers have all been optimised using the MM2 and gaussian optimisation calculation. The optimisation was completed using Job type: minimization, method: DFT=mpw1pw91 and the basis set: 6-31G(d,p). DOI links for the optimisation calculation can be found here: isomer 1 DOI:10042/24345 ,isomer 2 DOI:10042/24269 , isomer 3 DOI:10042/24268 , isomer 4 DOI:10042/24266 .
NMR Spectroscopic data for Cocaine isomers
After creating a .gif file containing the optimised molecules of cocaine, the NMR spectra have been computed by adding # mpw1pw91/6-31G(d,p), NMR scrf(cpcm,solvent=chloroform) to the first line of the text file and deleting all other lines. The calculation was then submited to the HPC service and deposted in the D-space. Literature proton NMR data [3], carbon NMR data [3].
DOI link for NMR calculations for cocaine 1:DOI:10042/24344
| Atom | Degeneracy | Calculated chemical shift (ppm) | Literature Chemical Shift (ppm) |
| 33 | 1 | 8.14 | n/a |
| 35 | 2 | 7.74 | n/a |
| 34 | 2 | 7.74 | n/a |
| 36 | 1 | 7.58 | n/a |
| 37 | 1 | 7.50 | n/a |
| 30 | 1 | 4.93 | 5.3 |
| 42 | 1 | 3.69 | 3.7 |
| 43 | 1 | 3.60 | 3.7 |
| 40 | 1 | 3.87 | 2.2 |
| 41 | 1 | 3.55 | 3.7 |
| 32 | 1 | 3.42 | 3.3 |
| 27 | 1 | 3.00 | 3.0 |
| 31 | 1 | 2.75 | 2.5 |
| 39 | 1 | 2.35 | 2.2 |
| 23 | 2 | 2.27 | n/a |
| 38 | 2 | 2.25 | 2.2 |
| 40 | 2 | 2.19 | 2.2 |
| 28 | 2 | 2.18 | 2.5 |
| 26 | 1 | 2.04 | 1.80 |
| 24 | 2 | 1.93 | n/a |
| 25 | 2 | 1.91 | n/a |
| 29 | 1 | 1.60 | 1.80 |
DOI link for NMR calculations for cocaine 2:DOI:10042/24273
| Atom | Degeneracy | Calculated chemical shift (ppm) | Literature Chemical Shift (ppm) |
| 33 | 1 | 8.10 | n/a |
| 35 | 4 | 7.93 | n/a |
| 37 | 4 | 7.88 | n/a |
| 34 | 4 | 7.87 | n/a |
| 36 | 4 | 7.83 | n/a |
| 39 | 1 | 5.72 | 5.5 |
| 30 | 1 | 4.98 | n/a |
| 38 | 1 | 3.94 | 3.6 |
| 40 | 1 | 3.87 | 3.6 |
| 32 | 1 | 3.23 | 3.5 |
| 27 | 1 | 3.00 | 3.3 |
| 31 | 1 | 2.80 | 3.10 |
| 28 | 3 | 2.37 | 2.4 |
| 24 | 3 | 2.33 | 2.1 |
| 25 | 3 | 2.29 | n/a |
| 42 | 3 | 2.12 | 2.4 |
| 43 | 3 | 2.08 | 2.4 |
| 41 | 3 | 2.03 | 2.4 |
| 23 | 1 | 1.75 | 1.80 |
| 26 | 1 | 1.65 | n/a |
| 29 | 1 | 1.30 | n/a |
Isomer 3 NMR data is shown below, here is the link to the calculation. DOI:10042/24274
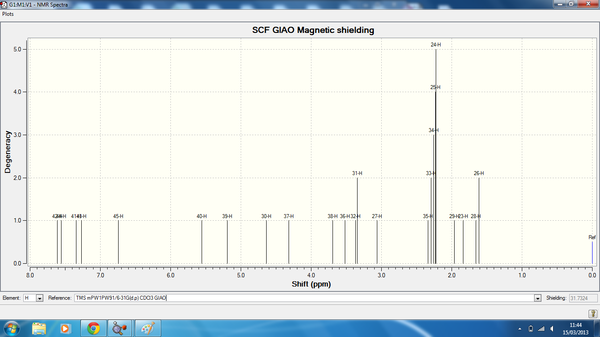
| Atom | Degeneracy | Calculated chemical shift (ppm) | Literature Chemical Shift (ppm) |
| 42 | 1 | 7.61 | n/a |
| 44 | 1 | 7.56 | n/a |
| 41 | 1 | 7.35 | n/a |
| 43 | 1 | 7.27 | n/a |
| 45 | 1 | 5.56 | n/a |
| 40 | 1 | 5.19 | 5.60 |
| 30 | 1 | 4.64 | n/a |
| 37 | 1 | 4.32 | 3.80 |
| 38 | 1 | 3.69 | 3.80 |
| 36 | 1 | 3.52 | 3.80 |
| 32 | 2 | 3.37 | 3.70 |
| 31 | 2 | 3.34 | 3.20 |
| 27 | 1 | 3.06 | 2.80 |
| 35 | 5 | 2.34 | 2.2 |
| 33 | 5 | 2.29 | 2.2 |
| 34 | 5 | 2.26 | 2.2 |
| 25 | 5 | 2.23 | n/a |
| 24 | 5 | 2.22 | 2.40 |
| 29 | 1 | 1.96 | n/a |
| 23 | 1 | 1.84 | 1.80 |
| 28 | 2 | 1.66 | n/a |
| 26 | 2 | 1.61 | n/a |
Isomer 4 NMR data is shown below, here is a link to the calculated data. DOI:10042/24275
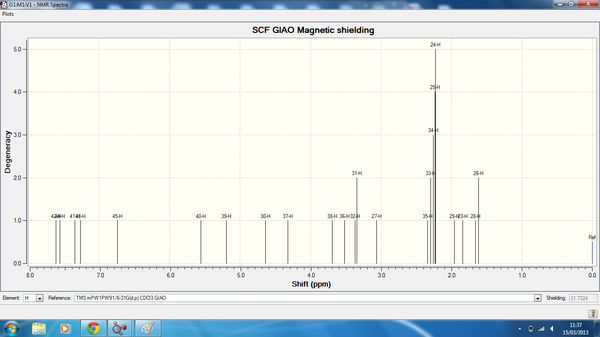
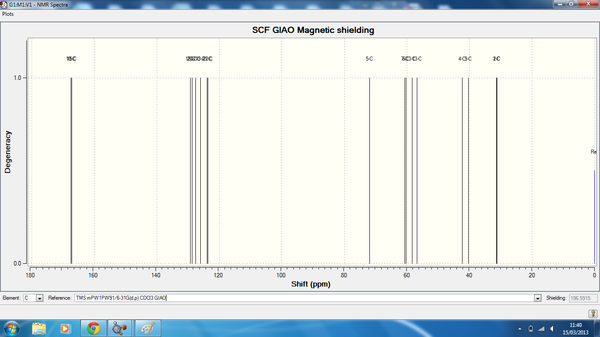
| Atom | Degeneracy | Calculated chemical shift (ppm) | Literature Chemical Shift (ppm) |
| 39 | 1 | 7.99 | n/a |
| 41 | 2 | 7.86 | n/a |
| 40 | 2 | 7.82 | n/a |
| 42 | 1 | 7.70 | n/a |
| 43 | 1 | 7.60 | n/a |
| 37 | 1 | 6.11 | 5.6 |
| 30 | 1 | 4.85 | n/a |
| 36 | 1 | 4.27 | 3.80 |
| 38 | 1 | 3.96 | 3.80 |
| 36 | 1 | 3.52 | 3.80 |
| 32 | 1 | 3.36 | 3.70 |
| 27 | 1 | 3.30 | 3.20 |
| 28 | 1 | 2.74 | 2.80 |
| 31 | 1 | 2.52 | 2.2 |
| 33 | 3 | 2.36 | 2.2 |
| 34 | 3 | 2.34 | 2.2 |
| 25 | 3 | 2.31 | n/a |
| 35 | 2 | 2.23 | 2.40 |
| 24 | 2 | 2.22 | n/a |
| 29 | 1 | 1.83 | 1.80 |
| 23 | 2 | 1.41 | n/a |
| 26 | 2 | 1.40 | n/a |
13CNMR summary table for isomers 1-4.
| Isomer 1 Calc(ppm) | Isomer 1 Lit(ppm) | Isomer 2 Calc(ppm) | Isomer 2 Lit(ppm) | Isomer 3 Calc(ppm) | Isomer 3 Lit(ppm) | Isomer 4 Calc(ppm) | Isomer 4 Lit(ppm) |
| 168.41 | 170.63 | 167.25 | 171.95 | 166.806 | 171.80 | 167.47 | 171.31 |
| 166.53 | 166.04 | 166.49 | 165.22 | 149.798 | 165.26 | 167.16 | 165.41 |
| 129.83 | 132.74 | 129.37 | 132.49 | 126.164 | 132.74 | 129.21 | 132.89 |
| 128.61 | 130.2 | 128.90 | 129.96 | 125.86 | 130.15 | 128.78 | 130.06 |
| 128.246 | 129.57 | 127.59 | 129.18 | 117.23 | 129.18 | 127.57 | 129.23 |
| 125.57 | 129.57 | 126.00 | 129.18 | 114.89 | 129.18 | 126.00 | 129.23 |
| 123.54 | 128.16 | 124.78 | 127.91 | 107.09 | 128.26 | 123.87 | 128.40 |
| 122.95 | 128.16 | 124.66 | 127.91 | 92.6248 | 128.26 | 123.59 | 128.40 |
| 74.23 | 66.82 | 72.70 | 67.64 | 67.03 | 67.69 | 71.92 | 68.18 |
| 58.50 | 64.76 | 61.59 | 62.38 | 61.74 | 62.87 | 60.64 | 61.01 |
| 57.14 | 61.45 | 59.37 | 59.50 | 60.83 | 60.48 | 60.27 | 59.60 |
| 51.71 | 51.26 | 53.94 | 51.55 | 55.77 | 51.65 | 58.31 | 51.40 |
| 42.22 | 41.02 | 41.21 | 48.38 | 41.38 | 41.51 | 42.34 | 40.38 |
| 30.92 | 35.46 | 33.01 | 39.88 | 37.36 | 40.12 | 36.15 | 36.63 |
| 29.98 | 25.32 | 31.88 | 33.56 | 27.12 | 24.97 | 31.38 | 25.52 |
| 28.92 | 25.17 | 31.50 | 26.63 | 26.56 | 24.22 | 31.37 | 24.05 |
In the 1HNMR spectrum there is an aromatic multiplet due to the benzonyl phenyl ring the calculated data has been included in the above tables and literature found this multiplet to be between 7.2-7.9ppm consistent with the calculated findings and as expected for an aromatic compound. Literature found that the OMe and NMe groups appear around 3.6 and 2.3ppm respectively [3]. Majority of the proton NMR data fits well with literature suggesting that the minimum structures have been found using the MM2 force field parameters, differences may be related to compound purity of the literature compound, geometry differences and NMR solvents. The solvent used to calculate the NMR data was chloroform as the literature compound was analysed in chloroform. It is now important to note the major differences between these spectra in terms of chemical potential the 5.5ppm region shows large deviation between isomers, however in-order to differentiate between the isomers information on the multiplicity of the peaks is needed [3]. Literature has reported that the 5.5ppm region shows a large difference in the multiplicity [3] of the four isomers thus one can differentiate between the four compounds when this information is available. The region approximately between 3.6-2.5ppm contains information relating to the C2, C1, and C5 protons for each of the isomers 1-4 and all show a difference in there chemical shifts with resonance within this region, this can be compared to C4, C6, C7 protons which appear in within and in close proximity to the 2.4-1.8ppm all show a difference in chemical environment and therefore a difference in resonance in this region is observed in the above data and spectrum's [3]. Literature [3] has shown the coupling constants for isomer 1 to be J1,2=3.3Hz,J1,5=1Hz, J2,3=6Hz, J2,4=0.8Hz. The presence of J1,5 is indicative for the cocaine isomer (1) as no other isomers show this coupling behavior along side the presence of J2,4 coupling although the latter is observed also for the allococaine isomer (3) it is a larger value of approximately 2.2Hz. A large coupling constant has been found from literature [3] for the allocoaine isomer (3)for the J4,4=15Hz while a smaller coupling has been shown for J3,5=1Hz these couplings and sizes are indicative of isomer 3 presence along with the added J4ax,5=3.8Hz. From this discussion so far the importance of coupling constant and multiplicity of each isomer is vital for the differentiation of the four compounds. Pseudococaine (2) [3] may be observed from the large coupling constants J2,5=10.9, J3,ax4=10.5Hz, J3,eq4=6.6Hz, J4,4=12.5Hz, this long range coupling is due to the extra stability of the chair conformation. Isomer (4) is harder to different by coupling constants, the couplings already discussed are also present for allopseudococaine (4) but are smaller in comparison showing no real characteristic individual couplings.
The assignment of the carbon NMR has been carried out using the assumption that the ortho carbons are expected to be more deshielded in comparison to the meta carbon in benzoate esters [3]. The MeO and and MeN are easily observed and as expected show a large difference in chemical shifts. The carbon NMR cannot be used to distinguish between isomers 1-4 of cocain [3]e. Most of the calculated data tabulated above shows good agreement with the literature [3], however there are a few outliers which don't fit to the other isomeric data and also deviate from the literature, when a difference of more than 5ppm is seen this is most likely due to inaccuracy of the geometry for particular carbon position s.
IR and Vibrational Spectra for Isomers of Cocaine
DOI links for the calculated IR spectrums and vibrational data can be found her for isomers 1-4; isomer 1DOI:10042/24342 , isomer 2DOI:10042/24278 , isomer 3DOI:10042/24279 and isomer 4DOI:10042/24280 .
Below are the IR vibrations for the cocaine isomers.
| Vibrational Mode | Vibrational Motion | Frequency (Cm-1) | Intensity | |||
| 34 |  |
716 | 63 | |||
| 73 |  |
1263 | 295 | |||
| 75 | 
|
1287 | 88 | |||
| 76 |  |
1291 | 179 | |||
| 101 |  |
1802 | 271 | |||
| 102 |  |
1818 | 248 | |||
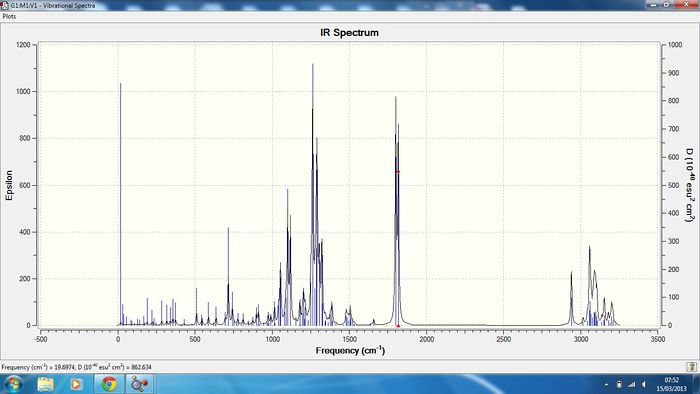
Isomer 1 Sum of electronic and thermal Free Energies= -1015.818955
| Vibrational Mode | Vibrational Motion | Frequency (Cm-1) | Intensity | |||
| 36 |  |
730 | 36 | |||
| 74 |  |
1270 | 318 | |||
| 75 |  |
1287 | 128 | |||
| 76 |  |
1294 | 116 | |||
| 77 |  |
1300 | 59 | |||
| 101 |  |
1815.84 | 281 | |||
| 102 |  |
1835 | 310 | |||
| 117 |  |
3133 | 40 | |||
Isomer 2 Sum of electronic and thermal Free Energies= -1015.794988
| Vibrational Mode | Vibrational Motion | Frequency (Cm-1) | Intensity | |||
| 38 |  |
765 | 49 | |||
| 55 |  |
1032 | 169 | |||
| 57 |  |
1058 | 62 | |||
| 62 |  |
1135 | 70 | |||
| 70 |  |
1203 | 313 | |||
| 71 |  |
1206 | 122 | |||
| 76 |  |
1268 | 221 | |||
| 77 |  |
1275 | 109 | |||
| 106 |  |
1813 | 239 | |||
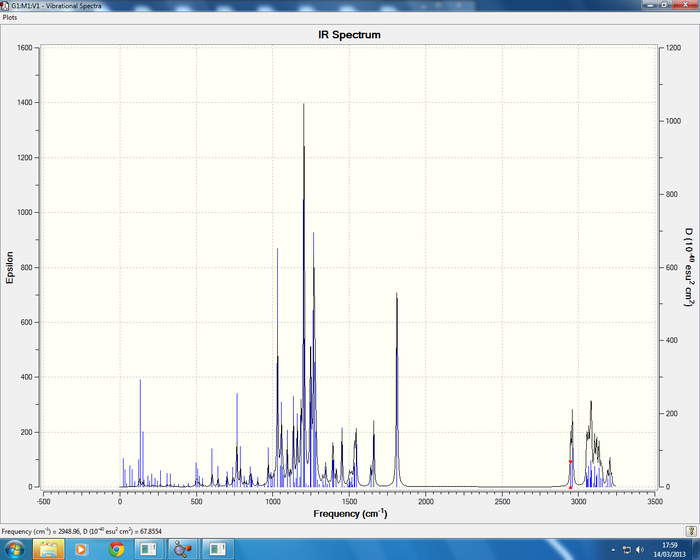
Isomer 3 Sum of electronic and thermal Free Energies= -1016.954104
| Vibrational Mode | Vibrational Motion | Frequency (Cm-1) | Intensity | |||
| 35 |  |
718 | 57 | |||
| 58 |  |
1071 | 82 | |||
| 60 |  |
1101 | 140 | |||
| 61 |  |
1119 | 109 | |||
| 65 |  |
1172 | 56 | |||
| 72 |  |
1260 | 92 | |||
| 74 |  |
1278 | 259 | |||
| 76 |  |
1268 | 221 | |||
| 77 |  |
1305 | 131 | |||
| 102 |  |
1810 | 273 | |||
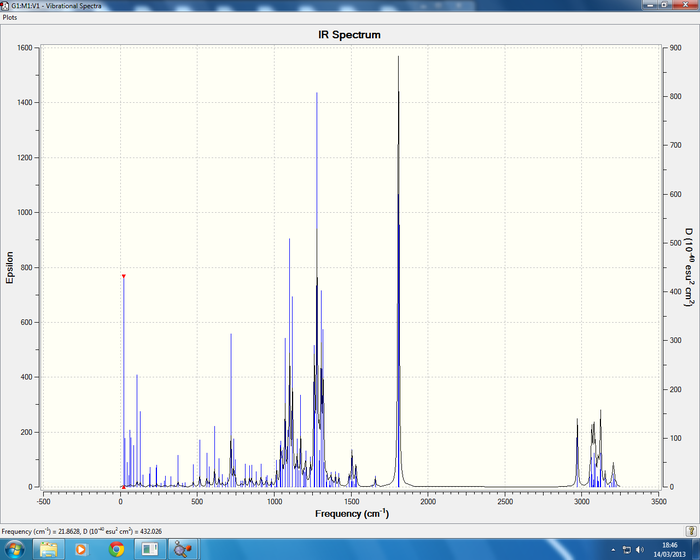
Isomer 4 Sum of electronic and thermal Free Energies= -1015.792895
All IR spectra are in good agreement with the literature data, cocaine (1) literature [2] report frequencies of 726, 1265, 1711, 1730cm-1 in comparison to the calculated data 716(C-H benzene ring bending), 1263(C-O stretching symmetric), and two C=O stretches which are symmetric at 1802 and 1818cm-1. The isomer of cocaine (2) pseudococaine literature [2] reports stretches at 1726, 1703, 1268, 712cm-1 in good agreement with the calculated data. In conclusion no information can be gained regarding the stereochemistry of the isomers from the IR data but the literature does report the correct stretches.
Electronic Circular Dichroism (CD/UV-visible spectra) for Isomers of Cocaine
Cocaine has four diastereisomers and each have two enatiomers leading to a total of eight possible isomers. Optical rotation and circular dichroism spectra can be used for the completed assignment of cocaine. The procedure works by measuring the difference of incidient light which is circular polarized, after passing through a compound of interest.
The DOI links for the CD and UV-Vis spectrum calculation can be found here for all isomers; isomer 1 DOI:10042/24339 , isomer 2 DOI:10042/24340 , isomer 3 DOI:10042/24341 and isomer 4 DOI:10042/24313
The literature [7] data has observed bands at 278 nm (positive), at 245 nm (negative), and at 222 nm (positive). Results have been recorded in methanol for the literature, in the attempt to assign L-Cocaine. The 245nm and 222nm bands have been assigned correctly but there is absence of the 278nm in the calculated spectrum, this could be due to an error in the literature interpretation of results and running of an experiment or it could be an error due to the calculation.
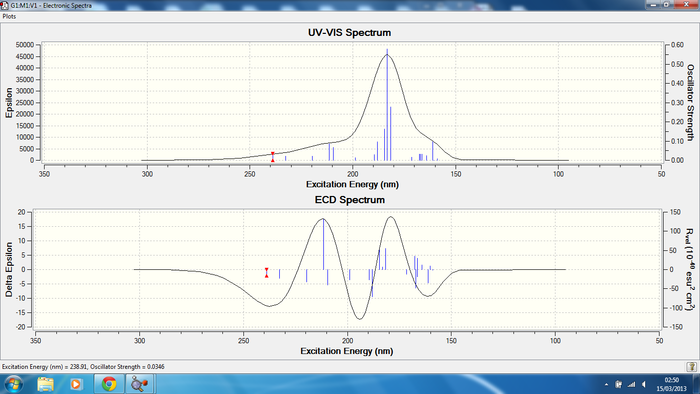
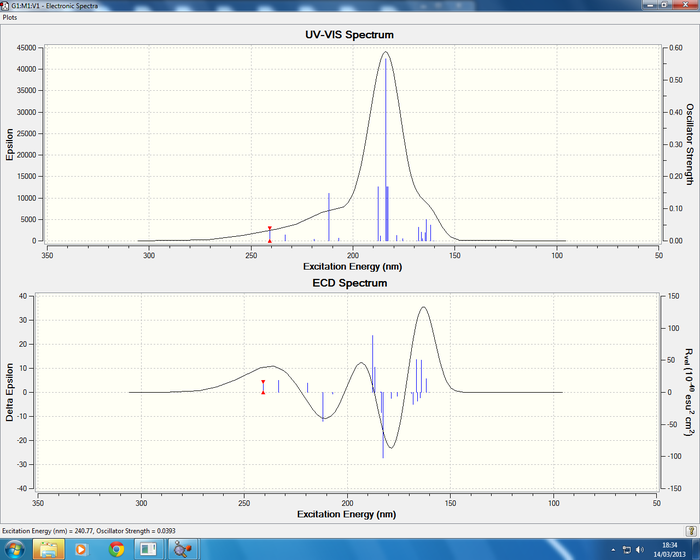
Density Functional Molecular Orbital Calculation for Cocaine Isomers 1-4
This calculation was completed using the optimised structures for isomers 1-4, the key word "pop=full" was added to the additional keyword box, the basis set used was 6-31G(d,p) and method DFT with job type set to a minimisation. The calculation was then sent to the HPC service and deposited in the Dspace.
DOI links for the MO calculation can be found here for each isomer, isomer 1 DOI:10042/24336 , isomer 2 DOI:10042/24337 , isomer 3 DOI:10042/24338 , isomer 4 DOI:10042/24312 .
| Isomer 1 |  |
 |
 |
 |
 |
| Orbital Energy | N=81 E=-0.21784 eV | N=82 E=-0.02857 eV | N=83 E=-0.00149 eV | N=84 E= 0.01636 eV | N=85 E= 0.05401 eV |
| Isomer 2 |  |
 |
 |
 |
 |
| Orbital Energy | N=81 E=-0.24934 eV | N=82 E=-0.04246 eV | N=83 E=-0.08880 eV | N=84 E= 0.01496 eV | N=85 E= 0.04402 eV |
| Isomer 3 |  |
 |
 |
 |
 |
| Orbital Energy | N=81 E=-0.23795 eV | N=82 E=-0.23163 eV | N=83 E=-0.00120 eV | N=84 E= 0.01098 eV | N=85 E= 0.01337 eV |
| Isomer 4 |  |
 |
 |
 |
 |
| Orbital Energy | N=80 E=-0.27127 eV | N=81 E=-0.23482 eV | N=82 E=-0.04049 eV | N=83 E=-0.00939 eV | N=84 E= 0.01078 eV |
The attention can now be drawn to the Molecular orbitals, firstly all MO show a different electronic distribution this is due to the change in symmetry due to a change in geometry for the diasterisomers, whereas enatiomers would show identical molecular orbitals as expected. However no information can be gained regarding the assignment of the stereo-chemistry of the isomers.
Conclusion
In conclusion to determine between enatiomers of cocaine optical rotation methods need to be carried out, in this case the calculations have been submitted but were running for a period longer than 48hours on the HPC service. The NMR spectrum are qualitative in determining the difference between the diasterisomers. It has been proven in the court of law and justice that the differentiation of these isomers and enantiomers is important, and lead to the change in motion of law in America regarding the conviction of cocaine. For more information follow this link:https://bulk.resource.org/courts.gov/c/F2/552/552.F2d.273.76-1140.html
Reference Section 2
- ↑ L. Paquette, N. A. Pegg, D. Toops, G. D. Maynard, R. D. Rogers, J. Am. Chem. Soc.,, 1990, 112, 277-283. DOI:10.1021/ja00157a043
- ↑ 2.0 2.1 2.2 http://library-resources.cqu.edu.au/JFS/PDF/vol_26/iss_1/JFS261810012.pdf ALLEN ET AL " COCAINE, A. C. Allen, ~ B.S.; D. A. Cooper, l B.S.; W. O. Kiser,2 B.S.; and R. C. Cottreli,2 M.S.
- ↑ 3.00 3.01 3.02 3.03 3.04 3.05 3.06 3.07 3.08 3.09 3.10 3.11 3.12 3.13 3.14 3.15 3.16 3.17 F.I Carroll, M.L Coleman and A.H Lewin, J. org. Chem. 1982, 47, 13-19.
- ↑ ^ Dalton, Louisa (2003-12-22). Chemical & Engineering News 81 (51): 37. Error: Bad DOI specified!
- ↑ 5.0 5.1 Karplus, Martin (1959). J. Chem. Phys. 30 (1): 11–15. Error: Bad DOI specified!
- ↑ John F. Casale, Forensic Science International 33, 275-298 (1987)
- ↑ John M,, Bowen and Neil Purdie, Anal. Chem. 1981, 53, 2237-2239