Rep:Mod:LWL01255539
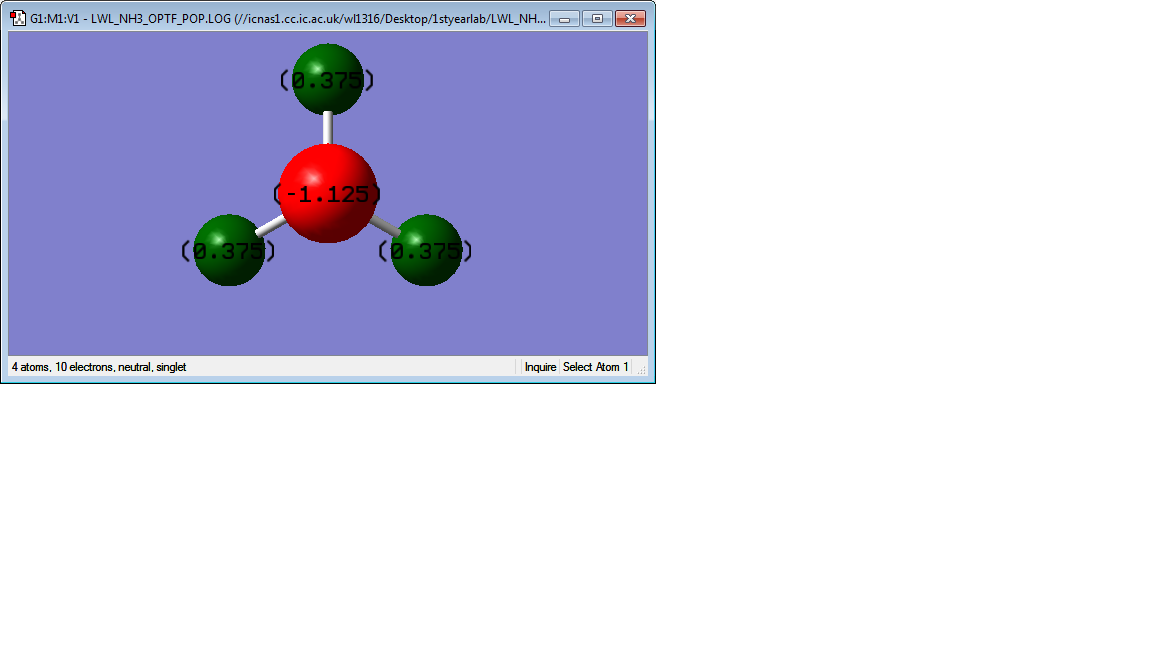
NH3 molecule
Optimized results
| Molecule name | Calculation Method | Basis Set | Total Energy | RMS Gradient Norm | Bond length(N-H) | Bond angle(H-N-H) | Point group |
|---|---|---|---|---|---|---|---|
| NH3 molecule | RB3LYP | 6-31G(D,P) | -56.55776873 a.u. | 0.00000485 a.u. | 1.01798Å | 105.741° | C3V |
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES Predicted change in Energy=-5.986270D-10 Optimization completed. -- Stationary point found.
Picture of NH3 molecule
NH3 molecule |
The optimisation file is linked to here
Picture of Vibrations Display
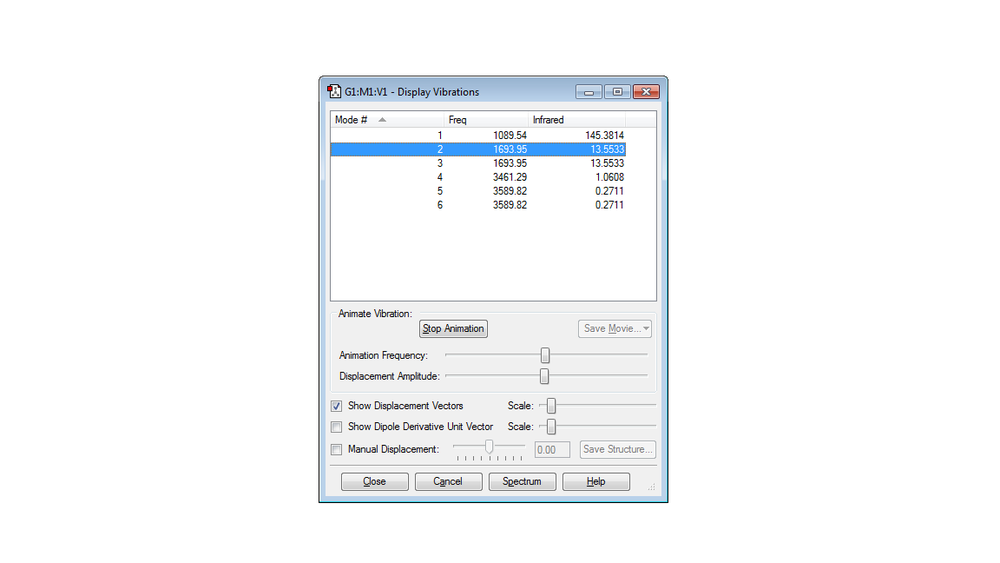
Six modes should be expected from 3N-6 rule, since N equals to 4 in this case.
The second and the third modes are degenerate due to the same frequency, as well as the fifth and the sixth modes are degenerate as well.
The first and the second modes are bending vibrations, while the rest of the modes are all bond stretch.
Mode 1 is highly symmetric since all the hydrogens are basically doing the same thing. Mode 4 is quite symmetric as well.
Mode 1 is the umbrella mode. When the hydrogens are bending, the vibration is very much similar to an umbrella being opened and closed.
Two bands would be expected to see in the spectrum. As mentioned above, mode 2 and 3 are degenerate, mode 5 and 6 are degenerate, so in theory 4 bands would be seen from the spectrum. However the intensity of mode 4,5 and 6 are too small (around 0-1) compared to the intensity of mode 1(around 145), so it would not be seen clearly in the spectrum. As for mode 2 and 3, they are degenerate so the intensity of this band should be the sum of the two which is around 26 and it is comparable to the intensity of mode 1 so this band would be seen. As a result, two bands would be expected to see in the spectrum.
Charge distributions
The charge on N atom is calculated to be -1.125 while that on H is calculated to be +0.375.
The charge on N is expected to be negative and that on H is expected to be positive, because the electronegativity of N is larger than H atom [1]
H2 molecule
Optimized results
| Molecule name | Calculation Method | Basis Set | Total Energy | RMS Gradient Norm | Bond length(N-H) | Bond angle(H-N-H) | Point group |
|---|---|---|---|---|---|---|---|
| H2 molecule | RB3LYP | 6-31G(D,P) | -1.17853935 a.u. | 0.00003809 a.u. | 0.74289Å | 180° | D∞H |
Item Value Threshold Converged? Maximum Force 0.000066 0.000450 YES RMS Force 0.000066 0.000300 YES Maximum Displacement 0.000087 0.001800 YES RMS Displacement 0.000123 0.001200 YES Predicted change in Energy=-5.726834D-09 Optimization completed. -- Stationary point found.
Picture of H2 molecule
H2 molecule |
The optimisation file is linked to here
Picture of Vibrations Display
Charge distributions
The charges on both H atoms are expected to be 0. Because there is no electronegativity difference between the two identical atoms, the electrons are equally attracted to either atom. As a result there is no charge on both atoms.
N2 molecule
Optimized results
| Molecule name | Calculation Method | Basis Set | Total Energy | RMS Gradient Norm | Bond length(N-H) | Bond angle(H-N-H) | Point group |
|---|---|---|---|---|---|---|---|
| N2 molecule | RB3LYP | 6-31G(D,P) | -109.52412866 a.u. | 0.00012538 a.u. | 1.10557Å | 180° | D∞H |
Item Value Threshold Converged? Maximum Force 0.000217 0.000450 YES RMS Force 0.000217 0.000300 YES Maximum Displacement 0.000068 0.001800 YES RMS Displacement 0.000096 0.001200 YES Predicted change in Energy=-1.474672D-08 Optimization completed. -- Stationary point found.
Picture of N2 molecule
N2 molecule |
The optimisation file is linked to here
Picture of Vibrations Display
Charge distributions
The charges on both N atoms are expected to be 0. Because there is no electronegativity difference between the two identical atoms, the electrons are equally attracted to either atom. As a result there is no charge on both atoms.
The Haber-Bosch process
Equation
N2 + 3H2→2NH3
Energy calculation
E(NH3)= -56.55776873 a.u.
2*E(NH3)= -113.1155375 a.u.
E(N2)= -109.52412866 a.u.
E(H2)= -1.17853935 a.u.
3*E(H2)= -3.53561805 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579079 a.u. = -146.48 kJ/mol
Since the energy change of converting gaseous hydrogen and nitrogen to ammonia is negative, the ammonia product is more stable.
However the literature value for the enthalpy change of this reaction is about -91.8 kJ/mol, which is really different from the result calculated from Gaussview. It could be explained that the energies used to calculate in Gaussview are the lowest in theory, but in reality not all molecules stay at the lowest energy all the time, therefore some differences might occur. Also the force fields used in the software and in the experiment in reality are different, therefore difference may occur as well.[1]
F2 molecule
Optimized results
| Molecule name | Calculation Method | Basis Set | Total Energy | RMS Gradient Norm | Bond length(N-H) | Bond angle(H-N-H) | Point group |
|---|---|---|---|---|---|---|---|
| F2 molecule | RB3LYP | 6-31G(D,P) | -199.48656514 a.u. | 0.07071498 a.u. | 1.29000Å | 180° | D∞H |
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES Predicted change in Energy=-4.818641D-14 Optimization completed. -- Stationary point found.
Picture of F2 molecule
F2 molecule |
The optimisation file is linked to here
Picture of Vibrations Display

Charge distributions
The charges on both F atoms are expected to be 0. Because there is no electronegativity difference between the two identical atoms, the electrons are equally attracted to either atom. As a result there is no charge on both atoms.
Picture of 1st MO
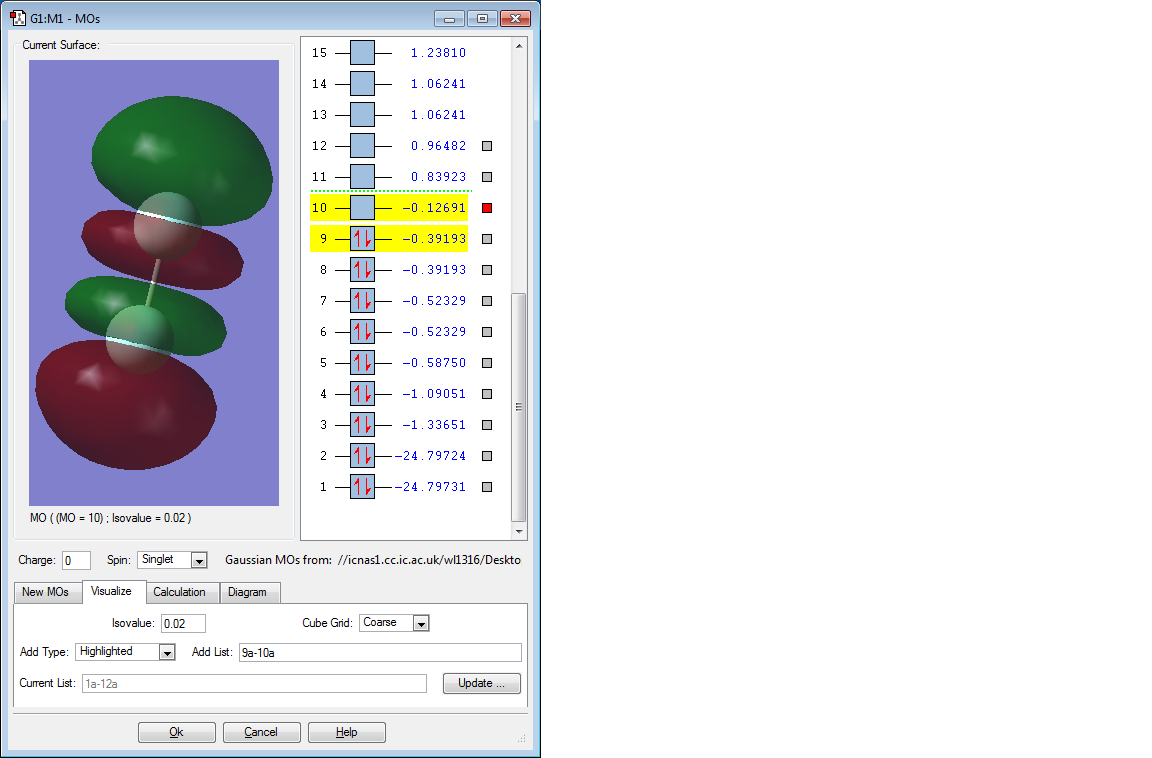
Discussion of 1st MO
This molecular orbital is the б* orbital formed by two 2p AOs, which is the LUMO. It is an unoccupied antibonding orbital and it is low in energy (-0.12691 a.u.), thus it is more likely to accept electrons.
F2 has a strong oxidising strength, suggesting this molecule has a tendency to accept electrons, which copes with the conclusion above, as a result the conclusion should be reliable.[1]
Picture of 2nd MO
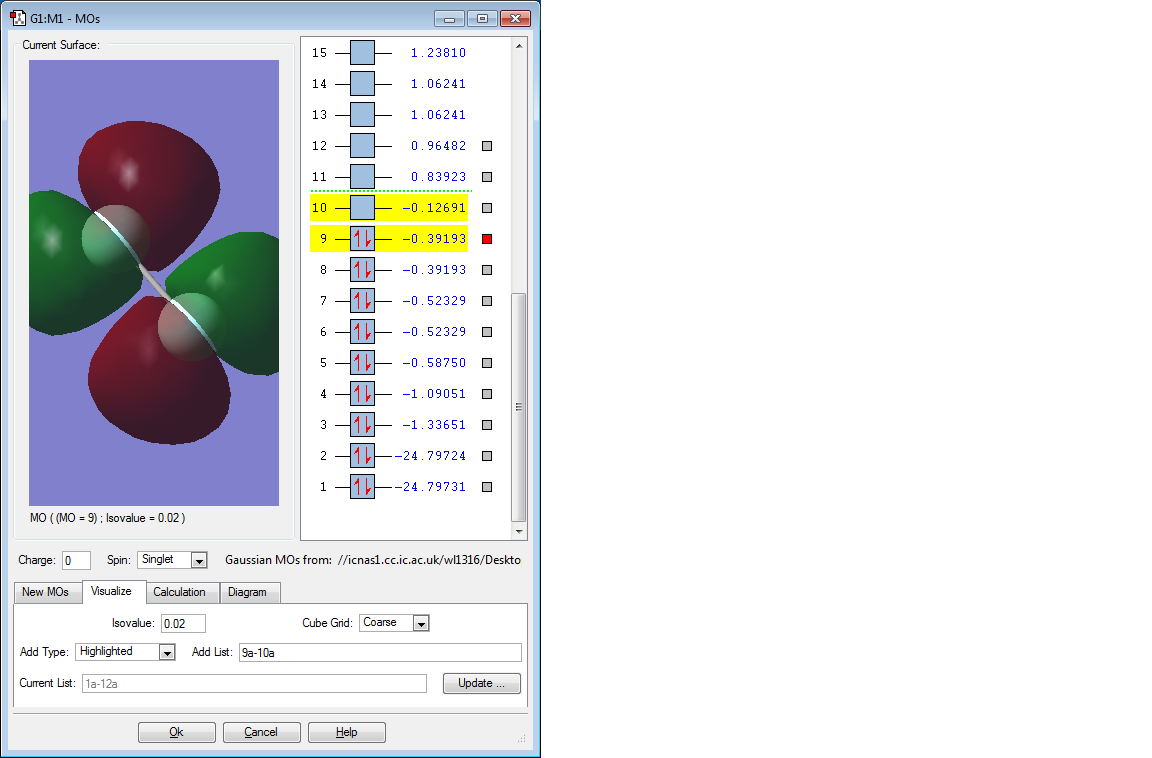
Discussion of 2nd MO
This molecular orbital is the π* orbital formed by two 2p AOs, which is the HOMO. And it is degenerate with the MO below it, because two 2p orbitals from one F atom both form π orbitals, therefore 2 MOs are generated. It is an occupied antibonding orbital and it is low in energy (-0.39193 a.u.), as a result electrons are not easy to lose from F2 molecules and it copes with the strong oxidising strength mentioned above.
Picture of 3rd MO
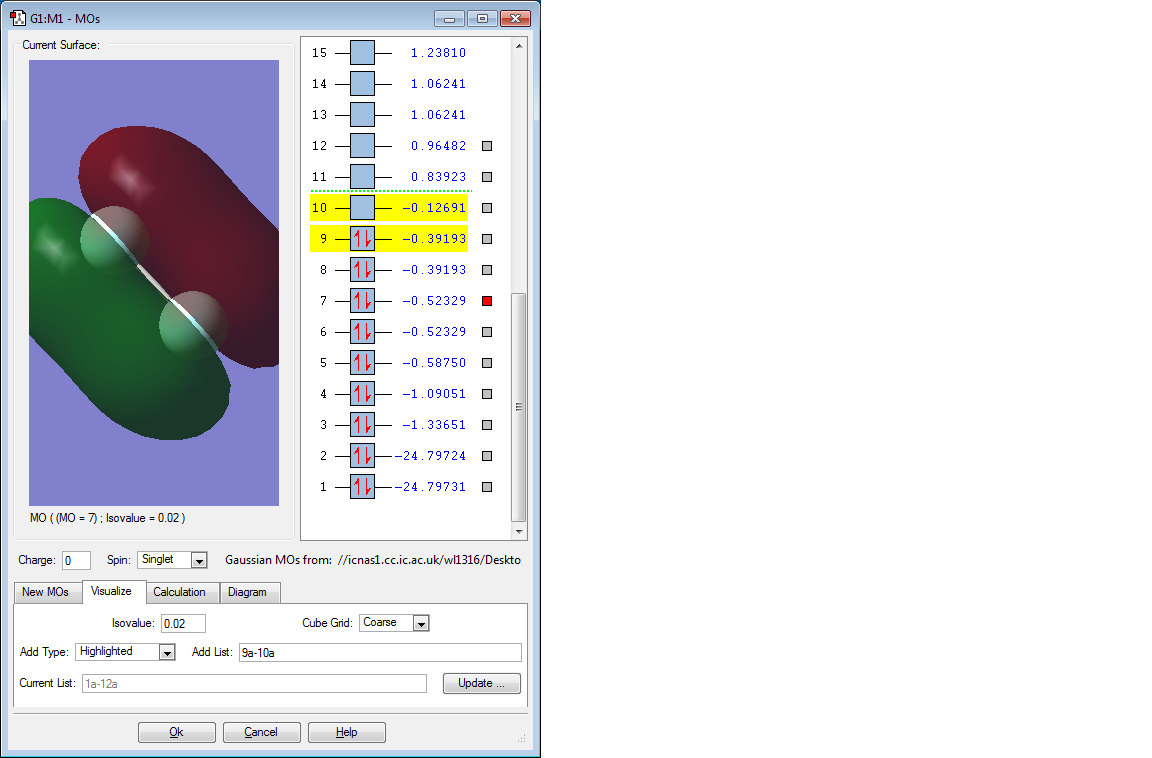
Discussion of 3rd MO
This molecular orbital is the π orbital formed by two 2p AOs. It is an occupied bonding orbital and it is low in energy (-0.52329 a.u.). And it is degenerate with the MO below it as 2p orbitals from 1 F atom contribute to the π orbital therefore 2π MOs are formed. Two 2π orbitals are formed, electrons are delocalised and in theory the molecule should be stable, however the sizes of the F atoms are so small that the stablisation is not very obvious, therefore F2 molecule is highly reactive. [1]
Picture of 4th MO
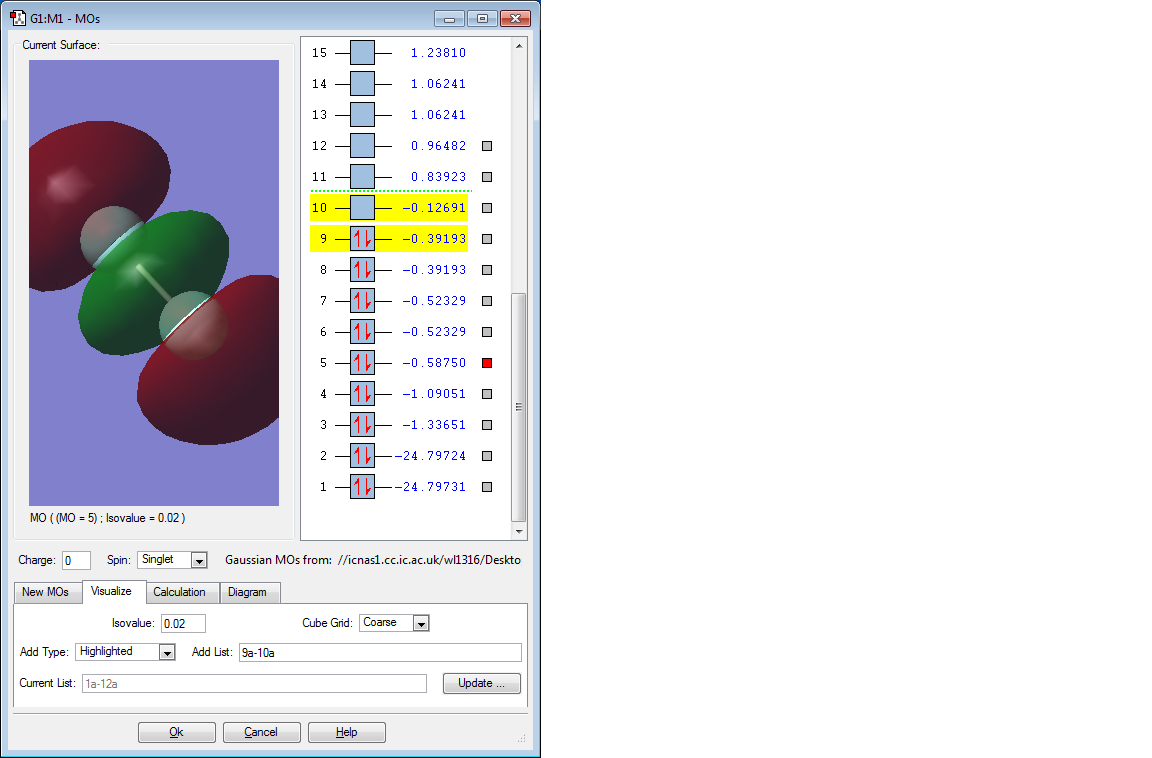
Discussion of 4th MO
This molecular orbital is the б orbital formed by two 2p AOs. It is an occupied bonding orbital and it is low in energy (-0.58750 a.u.).
Picture of 5th MO

Discussion of 5th MO
This molecular orbital is the б* orbital formed by two 2s AOs. It is an occupied antibonding orbital and it is low in energy (-1.09051 a.u.).