Rep:Mod:LS1109crashbangwallopwhatavideo
Module 3: Luke Squire-Smith
The Cope Rearrangement of 1,5-Hexadiene
Introduction

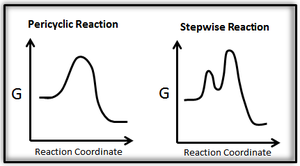
A pericyclic reaction is defined as "a chemical reaction in which a concerted reorganization of bonding takes place throughout a cyclic array of continuously bonded atoms. It may be viewed as a reaction proceeding through a fully conjugated cyclic transition state."[1]. There are no intermediates in a pericyclic reaction.
1,5-Hexadiene undergoes a Cope [3,3] sigmatropic rearrangement (a pericyclic reaction) via an aromatic "loose-chair" transition state[2], to form an identical product. Another, higher energy "boat" transition state is possible however, and both TS conformations will be explored with various modelling techniques (The Semi-empirical AM1 and the HF/3-21G levels of theory) to prove their efficacy.
Modelling techniques are able to predict the molecular orbital symmetries in the reactants and the adducts in this classic Diels Alder reaction, whose reactivity may be predicted and is explained by Woodward-Hoffman Rules[3]
Throughout, Gaussian 09W was used to perform calculations. GaussView 5.09 was the graphical interface used to create/optimise molecules and display results produced by Gaussian 09W.
.
Determining The Optimum Conformation of 1,5-Hexadiene
1,5-Hexadiene was constructed in GaussView 5.09 in the "Anti 1" conformation. The molecule was then cleaned with GaussView and optimised using an HF method and 3-21G basis set. Optimised structures (using the same method) were then obtained for the remaining anti and gauche conformations of 1,5-Hexadiene. All optimised conformations were determined as minima through frequency optimisation calculations, and their energies and symmetries are shown below:
| Conformation | Energy (Ha) | Jmol | Point Group | Rel. ΔE(Kcalmol-1) |
| [Anti 1] | -231.692602 | C2 | 0.0370 | |
| [Anti 2] | -231.692535 | Ci | 0.0791 | |
| [Anti 3] | -231.689071 | C2h | 2.25 | |
| [Anti 4] | -231.690971 | C1 | 1.06 | |
| [Gauche 1] | -231.683029 | C2 | 6.04 | |
| [Gauche 2] | -231.691667 | C2 | 0.624 | |
| [Gauche 3] | -231.692661 | C1 | 0 | |
| [Gauche 4] | -231.691530 | C2 | 0.710 | |
| [Gauche 5] | -231.689616 | C1 | 1.91 | |
| [Gauche 6] | -231.689160 | C1 | 2.20 |
Figure 1:
It is interesting to note that low frequency vibrations (<200cm-1) which involve roatation of atoms in the molecule about a C-C σ-bond, will readily occur at room temperature (298K) (e.g. Vib1 Vib2 Vib3), and so all these confomers will readily interconvert via rotation of C-C σ-bonds at RTP, with the major confomers having the lowest energy (e.g. Anti 1 ,Anti 2, Gauche 3).
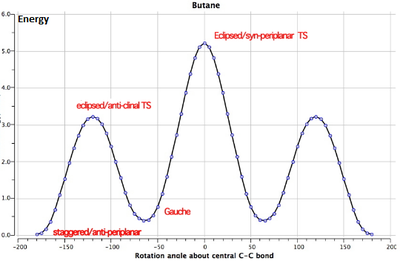
It can be seen from this table that the lowest energy conformation of 1,5-Hexadiene was calculated to be the Gauche 3 confomer by the HF/3-21G method and basis set. This result is questionable due to the primitive nature of the 3-21G basis set and its contradiction to expectation - one would expect an antiperiplanar conformation to be lower in energy for such a molecule(see image for energy profile of butane)[4]. Nonetheless, gauche conformations are often able to take advantage of increased favourable Van der Waals forces. The three lowest energy conformations (Anti 1 (C2), Anti 2 (Ci) and Gauche 3 (C1)) were recalculated using the more representative and accurate DFT-B3LPY/6-31G* method and basis set. The results for these optimisations are shown below in Figure 2.
In Figure 2, when modelling with a higher level of theory, it can be seen that now the antiperiplanar structures (Anti 1 & Anti 2) are more stable than the Gauche conformation which agrees with convention. The Anti 1 confomer is marginally more stable (by 0.0533 kcalmol-1) than the Anti 2 confomer, which is over 0.2kcalmol-1 more stable than the Gauche 3 conformation. The increased stability of the Anti confomers is due to optimum alignment of atoms in the molecule for hyperconjugative effects with respect to the gauche confomers. The DFT calculations were found to agree strongly with literature, and frequency optimisation showed no imaginary frequencies, confirming the confomers had been optimised successfully[5]
The increased stability of the Gauche 3 confomer with respect to other gauche confomers may be attributed to π-π orbital interactions observed in the HOMO and HOMO-1 (shown right).
Also interesting to note is the increased stability observed by using the higher level of theory. Conformations were optimised to be ~3Ha lower using the DFT methods (although comparison is strictly not allowed). This is a very large energy difference and one would think highlights the efficacy (and accuracy) of the higher levels of theory when optimising these confomers. Rather suprisingly however, minimal variations in bond lengths, bond angles and dihedral angles are observed between the different levels of theory.
| Conformation | Energy [6-31G* Opt] (Ha) | Jmol [6-31G* Opt] | Point Group | Rel. ΔE(kcalmol-1) |
| [Anti] 1 | -234.610334 | C2 | 0 | |
| [Anti 2] | -234.610249 | Ci | 0.0533 | |
| [Gauche 3] | -234.609861 | C1 | -0.297 |
Figure 2:
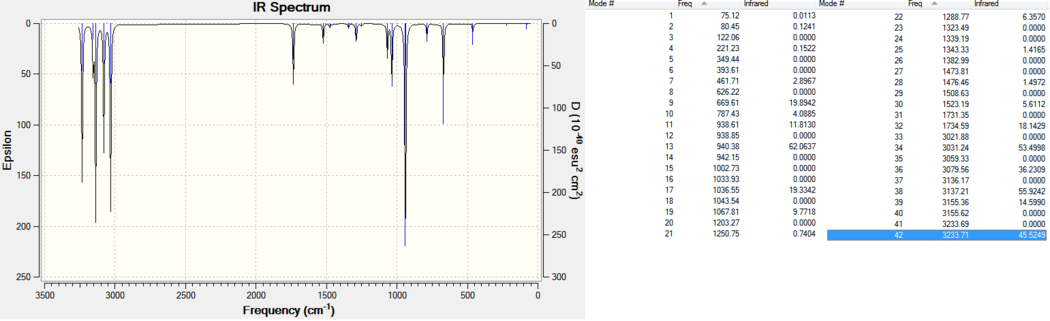
Shown below is the Infrared Spectrum of the DFT-B3LYP/6-31G* frequency optimised Anti 2 confomer:
Shown below is a classic C=C stretch, which was found at 1735cm-1 (please click if not animated):
Investigating Thermochemical Data of The Lowest Energy Confomers
Thermochemical data was extracted from the LOG files of the frequency-optimised Anti 1, Anti 2 and Gauche 3 confomers, and is shown below in Figure 3.
Σ(Eelec + ZPE) represents the potential energy at 0 K including the zero-point vibrational energy.
Σ(E + Evib + Erot + Etrans) represents the energy at 298.15 K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes at this temperature.
Σ(RT correction(H = E + RT)) represents an additional correction for RT (H = E + RT). This is mainly impoerant when investigating dissociative reactions.
Σ(Entropic cont. to G (G = H - TS)) represents the inclusion of the entropic contribution to the free energy (G = H - TS)
All of these values were calculated at 298.15K and 0K for the three confomers listed below (in order to get the Gaussian calculation to run, 0K was listed as 0.0001K):
| Conformation | Σ(Eelec + ZPE) [0 K] | Σ(E + Evib + Erot + Etrans) [0 K] | Σ(RT correction(H = E + RT)) [0 K] | Σ(Entropic cont. to G (G = H - TS)) [0 K] |
| Anti 1 | -234.467533 [-234.467533] | -234.461984 [-234.467533] | -234.461040 [-234.467533] | -234.496274 [-234.467533] |
| Anti 2 | -234.467367 [-234.467367] | -234.461872 [-234.467367] | -234.460928 [-234.467367] | -234.496472 [-234.467367] |
| Gauche 3 | -234.466892 [-234.466892] | -234.461491 [-234.466892] | -234.460546 [-234.466892] | -234.495889 [-234.466892] |
Figure 3
These results clearly show that at 0K the only contribution to the energy of the molecule is the zero-point energy, which is logical, as this temperature is absolute zero and therefore there should be no additional contributions to the zero-point energy.
.
Variation of Σ(Eelec + ZPE), Σ(E + Evib + Erot + Etrans), Σ(RT correction(H = E + RT)), Σ(Entropic cont. to G (G = H - TS)) with Temperature
.
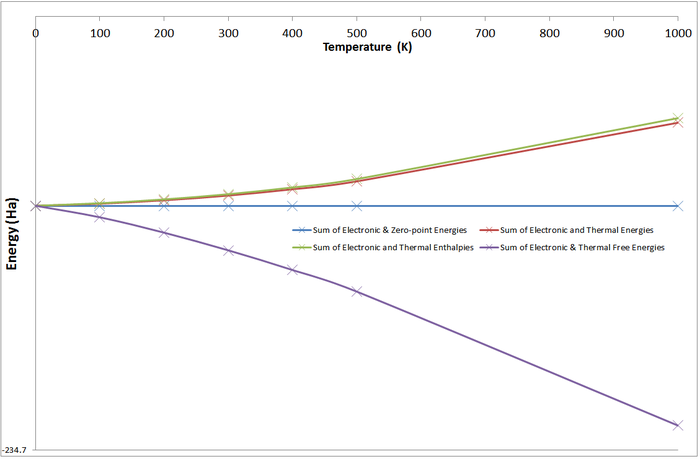
To investigate the variation of these contributions with energy, thermochemistry calculations were carried out on a range of temperatures between 0K and 1,000K (0K, 100K, 200K, 300K, 400K, 500K, 1000K) for the Anti 1 Confomer:
These results show that the zero-point energy of the system never changes, which is logical. As confirmed above, all other contributions are zero at 0K. The electronic & zero-point energies do not vary with temperature as this contributions cannot be altered and will be unchanged across any temperature.
As is logical, contributions from the translational, rotational, and vibrational energy modes will increase with increasing temperature - a molecule has a greater entropy at higher temperatures.
The free energy of the system decreases as a function of increasing temperature (G = H - TS). As temperature increases, the degrees of freedom available to the molecule through vibrational and rotational degrees of freedom increases.
.
Mini Conclusion
The semi-empircal AM1 level of theory was able to establish an ordering of confomer energies which was in rough agreement with what is expected. However, its primitive nature was highlighted by its failure to order the three lowest energy conformations, which were very similar in energy relative to other conformations.
Here the DFT-B3LYP/6-31G* higher level of theory demonstrated its usefulness. The Anti 1 confomer was determined to be the lowest energy, with Anti 2 second and Gauche 3 slightly higher.
The variation of the Thermochemical contributions with temperature were modelled for the Anti confomer and showed relationships in line with what is expected.
.
Optimising The Transition States for the Cope Rearrangement Reaction
Experimental
Various methods were considered for optimising the boat and chair transition states for this [3,3]-Sigmatropic Reaction:
1. Computing the force constants at the beginning of the calculation (Berny Transition State Method Using HF/3-21G Theory Level)
2. Using the redundant coordinate editor (Frozen Coordinate Method)
3. Using the QST2 method.
Berny Transition State Method Using HF/3-21G Theory Level

An allyl fragment (CH2CHCH2) was constructed and optimised with the HF/3-21G method and basis set in GaussView. Two optimised fragments were then oriented together to take the shape of a chair transition state, with the terminal C atoms of each allyl group approximately 2.2Å apart. After HF/3-21G optimisation, the C2h was constrcuted. The imaginary frequency at -817.9cm-1 was also observed, corresponding to the cope rearrangement (right).
.
Frozen Coordinate Method

The optimised "guess structure" for the TS was altered in a new file to be optimised (HF/3-21G) with a fixed distance between the terminal C atoms of the allyl fragment (the bond-forming/breaking distances) (2.2Å) and frozen coordinates, using the 'Redundant Coordinate Editor' . The optimised molecule was then further optimised using a transition state optimisation and removing the restrictions of the bond lengths at the terminal C atoms. This second optimisation resulted in significantly shorter bond-forming/breaking distances at 2.02Å .
The imaginary frequency corresponding to the bond-forming/breaking "vibration" was again 818cm-1 and is shown right.
.
Optimising The Boat Transition State Using The QST2 Method
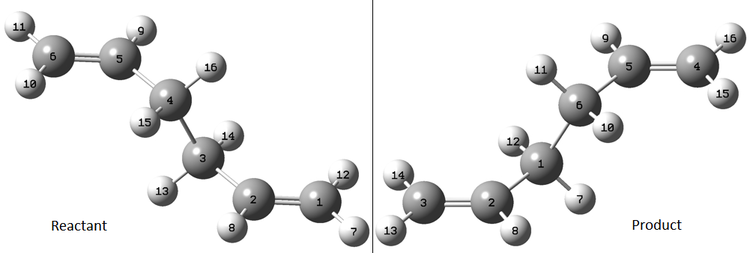
In order to optimise the boat transition state with this method, both the reactant molecule and the product molecule had to be specified. THe QST2 method is able to interpolate a transition state from the coordinates of these two molecules. To ensure this method resulted in a successful optimisation, the two molecules were labelled as below, to correspond to each other:
The initial optimisation failed because the model was not able to consider orientation of the molecule into the correct geometry for the boat TS via central C-C bond rotation from the initial geometries. Therefore, the conformations of both product and reactant were adjusted to produce the conformations shown below. The central C-C-C-C dihedral angle of the reactant (C2-C3-C4-C5) was changed to 0°, and the C2-C3-C4 and C3-C4-C5 bond angles were reduced to 100°. This was repeated accordingly for the product molecule. : The resulting optimisation produced a vibration at an imaginary frequency of -840cm-1, intensity 1.61, corresponding to the reversible [3,3] sigmatropic shift (shown right)
Intrinsic Reaction Coordinate Calculations For the Chair Transition State
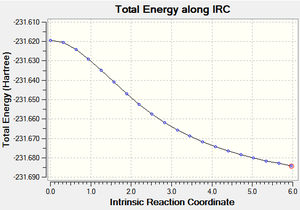
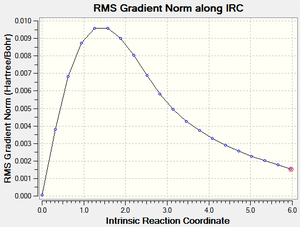

Taken from the transition state, the IRC calculation uses the imaginary frequency an extrapolates from this point to a lower energy local minimum - the likely conformation of the molecule which undergoes the rearrangement via the Chair TS.
Careful consideration of all conformations would suggest the Gauche 2 confomer to represent this local minimum as it would require minimal orientation to reach the desired shape for the Chair TS.
The initial IRC calculation was terminated after 20 steps and produced an incomplete IRC optimisation (below):

From this point, the structure was optimised using the HF/3-21G level of theory to the Gauche 2 confomer as shown below. The symmetry (C2) and the energy (231.691667Ha) were identical to the previously calculated values of the Gauche 2 confomer above. This is logical and was predicted above - the Gauche 2 confomer requires the least manipulation, and has the correct symmetry to look like the chair TS.
The alternative method of increasing the number of steps the IRC has to optimise the system as well as calculating the force constants at every step was also explored by increasing the maximum number of possible steps to 100 (the calculation terminated at 47, again producing a molecule (without its central C-C bond) resembling the Gauche 2 confomer):
.
Intrinsic Reaction Coordinate Calculations For the Boat Transition State
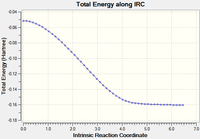
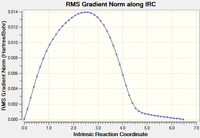
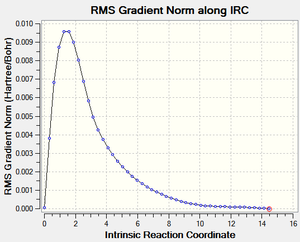
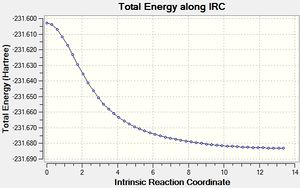
An IRC was then carried out on the boat transition state (Results shown below). The force constants were always calculated and the step maximum was set to 50. The IRC initially produced which was subsequently optimised to the Gauche 3 confomer using the HF/3-21G level of theory (confirmed by energy comparison).
| Total Energy Plot of The Boat IRC | RMS Gradient Plot of The Boat IRC |
|---|---|
|
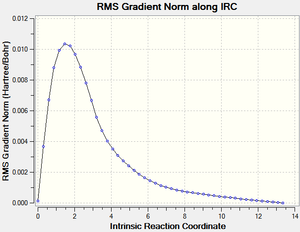
|
Transition State Activation Energies
In order to calculate the transition state activation energies, the lowest-calculated energy conformations of 1,5-Hexadiene were compared with the chair and boat transition state energies for both the HF/3-21G and DFT-B3LYP/6-31G* levels of theory.
With the HF/3-21G level of theory, the gauche 3 confomer was determined to be the lowest in energy. With the DFT-B3LYP/6-31G* level of theory the anti-1 was determined to be lowest in energy (the data is calculated at 298.15K unless stated):
| HF/3-21G | DFT-B3LYP/6-31G* | |||||||||
| Symmetry | Σ(electronic & zero-point energies) (0K) (Ha) | Σ((Electronic and) Thermal Energy) (Ha) | Forming Bond C-C Distance (Å) | Activation Energy* [0K] (kcalmol-1) | DFT Σ(electronic & zero-point energies) (0K) (Ha) | DFT Σ((Electronic and) Thermal Energy) (Ha) | Forming Bond C-C Distance (Å) | Activation Energy** [0k] (kcalmol-1) | Lit[6] (kcal/mol) | |
| Chair TS | C2h | -231.697023 | -231.691664 | 2.02 | 44.74 [45.56] | -234.562901 | -234.556982 | 1.97 | 33.48 [34.26] | 33.5 ± 0.5 |
| Boat TS | C2v | -231.60839 | -231.602801 | 2.14 | 56.39 [57.12] | -234.549026 | -234.543080 | 2.21 | 42.20 [43.09] | 44.7 ± 2.0 |
*Compared to the Gauche-3 Confomer **Compared to the Anti-1 confomer
- 1 hartree = 627.509 kcalmol-1
These results clearly demonstrate the higher accuracy of the DFT-B3LYP/6-31G* level of theory compared to the HF/3-21G through their stronger concordance with literature. The 3-21G calculations were out by over 10kcalmol-1. The results also show the activation energy of the reactions to be slightly greater (~1kcalmol-1) at 0K.
.
Diels Alder
In this section, the structure of the transition state of the Diels-Alder reaction between cis-butadiene and ethene will be characterised using Semi-empirical methods and the DFT-B3LYP/6-31G* level of theory. The MOs of the reactants and transition states will be modelled, and their symmetries determined, to gain a better understanding of the reaction, and its orientational requirements of the reactants.
.
Introduction
The Diels Alder reaction (a.k.a. the 'Mona Lisa Reaction') is the classic pericyclic reaction - a [π4s + π2s] cylcoaddition reaction between a diene and a dienophile, first documented by Diels and Alder (who achieved a Nobel Prize for their work) in 1928.
Stereochemistry governs the reaction, with two approaches possible - the endo approach or the exo approach (the reaction often giving unequal mixtures of these adducts)[7][8]. The stereochemistry of this reaction, and its effects on reactivity will be explroed in this section. The reverse of a Diels Alder reaction can occur, especially intramolecularly. This is known as a Retro-Diels Alder Reaction.
.
Experimental
cis-butadiene was optimised using the semi-empirical AM1 level of theory. Frequency analysis of this optimisation showed an imaginary frequency at -38cm-1 and so the dihedral angle of the molecule was moved away from zero and re-optimised to produce a molecule with a dihedral angle of 13.9o, which showed no imaginary frequencies.
The DFT-B3lYP/3-21G level of theory was able to optimise cis-butadiene to a planar conformation due to its ability to consider the conjugative effects that cis-butadiene shows.
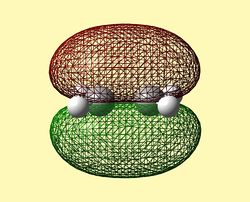
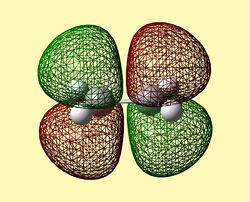
The Frontier Molecular Orbitals of cis-Butadiene and Ethene are shown below their symmetry with respect to the plane of symmetry is detailed):
| HOMO Butadiene (Antisymmetric) | LUMO Butadiene (Symmetric) | HOMO Ethene (Symmetric) | LUMO Ethene (Antisymmetric) |
|---|---|---|---|
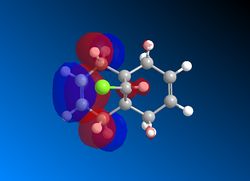
|
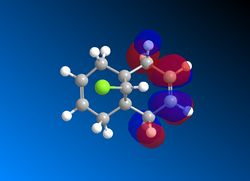
|
|
|
Computation of the Transition State Geometry of the Diels Alder Reaction Between cis-Butadiene and Ethene
The cis-butadiene and ethene fragments were oriented to reflect their predicted orientation in the transition state, with a distance between the terminal C atoms and the ethene C atoms set at 2.0Å pre-optimisation. The semi-empirical AM1 method was used to get a rough estimate of the transition state. The DFT-B3YLP/6-321G* level of theory was then used to refine this estimate. Frequency optimisation was used to confirm the transition states. The imaginary frequency vibrations - depicting the bond-forming/breaking processes of the transition state are depicted below:
The concerted vibrations shown above are in agreement with how the reaction is predicted to proceed - via concerted transfer of electron density. The presence of one imaginary frequency for each vibration demonstrates a transition state was reached in both cases.
In the AM1 level of theory, cis-butadiene C=C bond lengths were modelled at 1.38Å and the C-C bond at 1.40Å (reflecting the conjugated nature of this bond). In ethene, the C=C bond length was modelled at 1.38Å. The separation between the terminal C atoms of the reactants was 2.12Å.
In the DFT-B3LYP/6-31G* level of theory, cis-butadiene C=C bond lengths were modelled at 1.38Å and the C-C bond at 1.41Å. In ethene, the C=C bond length was modelled at 1.39Å. The separation between the terminal C atoms of the reactants was 2.27Å.
Considering the DFT-B3LYP/6-31G* level of theory, C=C bond lengths of butadiene are reported as 1.35Å with the C-C bond 1.46Å.[9]
In the transition state, one would expect the C=C bonds to be greater than 1.35Å, and the C-C bond to be less than 1.46Å which is what is observed. Furthemore, the distance between the terminal C atoms in cis-butadiene and ethene C atoms (2.12Å) is well within the doubled Van der Waals radii of C atoms (3.14Å), indicating the partial formation of a C-C bond between these atoms. Again, the equal distances for both termini of the butadiene molecule and ethene are consistent with the concerted nature of the electron transfer.
Furthermore, the vibrations above clearly show a transition from sp2 hybridised C atoms to sp3 hybridised C atoms, consistent with the cycloaddition reaction. The shortening of the central C-C bond in butadiene is also observed - in concordance with the formation of a C=C bond.
Below is the vibration lowest positive frequency (147cm-1) from the optimisation. It shows a rotation/asynchronous movement of the molecules in a twisting motion - the opposite to the way the bonds are formed in the TS (shown above). If this occured in the transition state, the formation of bonds would not be concerted:
MO Analysis
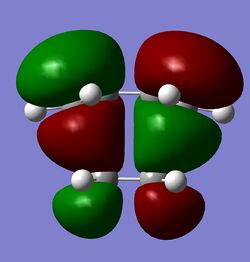
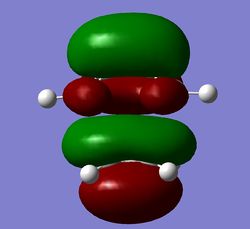
The molecular orbitals of the transition state are shown for the AM1 and 6-31G* levels of theory. The MOs clearly show interactions between the reactant molecules and the retention of symmetry from the fragment MOs. The symmetries of the MOs with respect to the plane of symmetry are shown below:
| TS HOMO (AM1) (Antisymmetric) | TS LUMO (AM1) (Symmetric) | TS HOMO (6-31G*) (Antisymmetric) | TS LUMO (6-31G*) (Symmetric) |
|---|---|---|---|
|

|
|
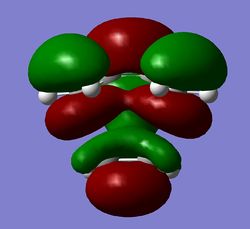
|
By considering the HOMO and LUMO of butadiene and ethene, as well as the Transition State HOMO & LUMO, it can be seen that the butadiene HOMO and ethene LUMO combine to form the TS HOMO. Both fragment orbitals are antisymmetric and combine to form an antisymmetric MO, preserving the symmetry. Moreover the symmetric butadiene LUMO and ethene HOMO combine to form the symmetric TS LUMO, again preserving the symmetry.
The TS HOMO clearly shows the interaction of the butadiene π-MOs with the ethene π*-MOs to form a C-C bond between the fragments. The TS LUMO interestingly shows an interaction of the ethene π-MO with the central portion of the butadiene π*-MO to form the new C=C bond in butadiene.
The Study of the Regioselectivity of the Diels-Alder Reaction
Introduction
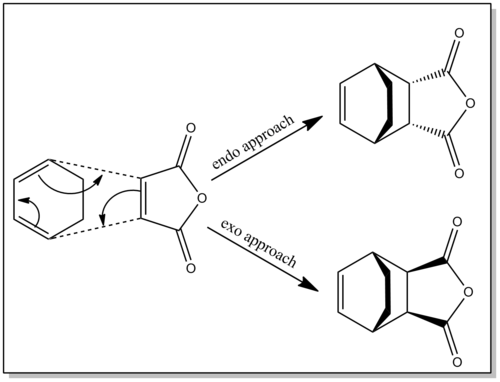
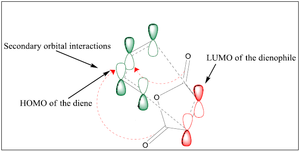
Maleic anhydride reacts with 1,3-cyclohexadiene via a Diels-Alder reaction with the major (and kinetic) adduct being formed through an endo transition state. Two approaches are in fact possible for this reaction, with the endo transition state having a lower activation energy than the exo transition state through superior secondary orbital interactions experienced through the endo approach. The exo product however is the thermodynamic product due to its final geometry giving rise to less steric strain.
In this section, the nature of the endo and exo transition states for this reaction will be studied to predict the kinetically controlled pathway of the reaction. Furthermore, the steric penalty of the endo approach and the favourable secondary orbital interactions associated with this approach will be considered. It has been shown in literature that the secondary orbital interactions outweigh the steric penalty, and this will be investigated here [10]
Experimental
The frozen coordinate method with the semi-empirical AM1 level of theory was used to optimise the fragments (which were pre optimised using HF/3-21G Levels of Theory) to their transition state using the same techniques as in the previous section. Frequency Optimisation was used to confirm the transition state, and the vibrations of the imaginary frequencies are shown below (please click if not animated). The vibrations show synchronous (concerted) formation of the C-C σ-bonds between the fragments.
| Approach | Calculated Freq. (cm-1) | Intensity | Animation (Please Click) | |
|---|---|---|---|---|
| Endo | -806 | 71.6 | 
| |
| Exo | -525 | 5.81 | 
|
Below is the vibration lowest positive frequency from the endo optimisation. It shows a rotation/asynchronous movement of the molecules in a twisting motion - the opposite to the way the bonds are formed in the TS (shown above). If this occured in the transition state, the formation of bonds would not be concerted.
Molecular Orbitals of the Reactants and Adducts
Shown below are the HOMO and LUMO of the Reactants. Here Maleic Anhydride's HOMO and 1,3-Cyclohexadienes LUMO are symmetric with respect to the plane of symmetry, with the LUMO and HOMO of the respective reactants antisymmetric. Only MOs of the same symmetry may combine:
| Maleic Anhydride HOMO (symmetric) | Maleic Anhydride LUMO (antisymmetric) | 1,3-Cyclohexadiene HOMO (antisymmetric) | 1,3-Cyclohexadiene LUMO (symmetric) |
|---|---|---|---|

|

|

|

|
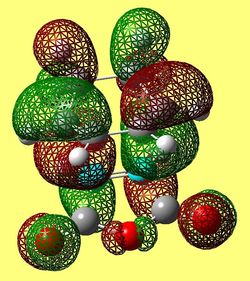
Shown below are the HOMO, LUMO and LUMO+1 of the ENDO and EXO Adducts. It is clearly obvious from the MOs above that only MOs of the same symmetry have combined to preserve symmetry:
| ENDO TS HOMO (Antisymmetric) | ENDO TS LUMO (Antisymmetric) | ENDO TS LUMO+1 (Symmetric) |
|---|---|---|
|
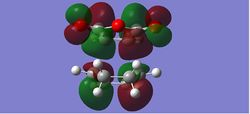
|
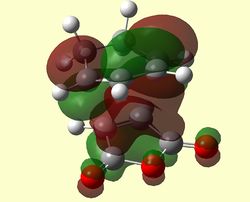
|
| EXO TS HOMO (Antisymmetric) | EXO TS LUMO (Antisymmetric) | EXO TS LUMO+1 (Symmetric) |
|---|---|---|
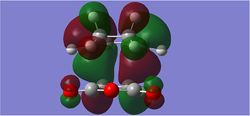
|

|
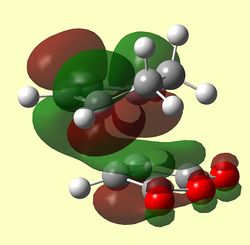
|
The LUMO +1 MOs of the endo TS clearly show secondary orbital interactions between the C=O π-bonds of maleic anhydride and the C=C π-bonds of butadiene, which have both the correct symmetry and orientation to overlap in the endo approach which is not available in the exo approach.
It is however hard to quantify the stabilisation-ability of the LUMO +1 due to its apparent antibonding nature. Nevertheless, close inspection of the modelled MO diagram shows this MO to be overall bonding (just) 0.02014ha. A secondary orbital stabilising effect therefore may come from occupation of this MO. In the Exo TS this MO is slightly higher in energy at -0.02013Ha.
The IRC pathway of the endo and exo transition states was then calculated to confirm a real transition state.
IRC
THe IRC .out files were then optimised using the AM1 level of theory to produce the endo and exo products, confirming the correct optimisation to a transition state:
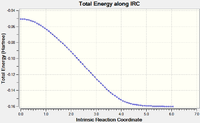
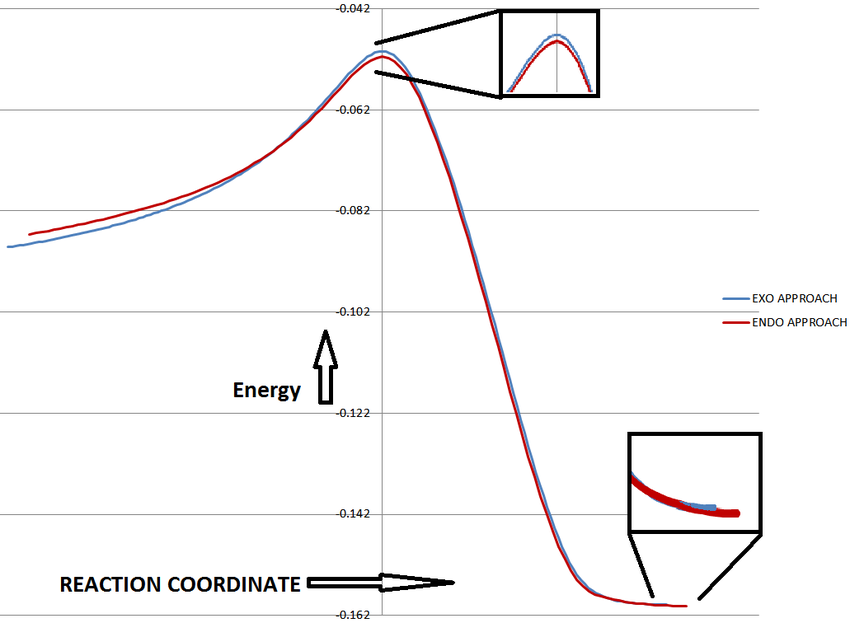
IRC was initially calculated in the forward direction only. However, in order to get a full appreciation of the reaction, the IRC was calculated in both directions to produce a plot of the energy of the system against the reaction coordinate (Reactants separated on left, Product on Right):
The reaction profiles for the endo and exo approaches clearly show that, although there is a small difference in energy, the endo approach has the lower activation energy and lower energy transition state in comparison to the exo approach. Furthermore, the endo adduct was deemed to be marginally lower in energy.
Although a very useful analysis, the primitive nature of the semi-empirical AM1 level of theory may not be fully representative of the reaction.
The Energies of the Final DFT Level Optimised Structures: The Kinetic and Thermodynamic Products
Both the Endo and Exo adducts were optimised using the DFT-B3LYP/6-31G* level of theory (due to the inadequacies of the semi-empirical AM1 level of theory) to determine whether the Endo or Exo adduct was the thermodynamic product:
Endo Adduct
File Name = ENDO DFT OPT File Type = .fch Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 6-31G(D) Charge = 0 Spin = Singlet Total Energy = -613.99109085 a.u. RMS Gradient Norm = 0.00000281 a.u. Imaginary Freq = Dipole Moment = 4.9392 Debye Point Group =
Exo Adduct
File Name = EXO DFT OPT File Type = .fch Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 6-31G(D) Charge = 0 Spin = Singlet Total Energy = -613.99109082 a.u. RMS Gradient Norm = 0.00001885 a.u. Imaginary Freq = Dipole Moment = 4.9394 Debye Point Group =
It can be seen that even at a much higher level of theory, it is very difficult to determine which adduct is more stable, with the endo product winning here (marginally, by less than 0.00002kcalmol-1). This may be to the maleic anhydride-like fragment occupying an axial position on the ring, anti to the cyclohexene bridge, which one might consider to be more favourable than this group occupying an equatorial position.
Conclusion
It was determined through semi-empirical methods and DFT-B3LYP levels of theory that the endo approach is the kinetic approach. Although the transition state for this reaction is under more steric strain due to repulsions between reactants, this effect is more than compensated for by the secondary orbital interactions between the conjugated π-systems of both molecules, leading to an overall lowering of energy of the transition state with respect to the exo approach, where these interactions are not possible.
Furthermore it was determined that the endo product in this case was the thermodynamic product, perhaps due to the bulky anhydride ring occupying an axial position anti to the cyclohexene bridgehead.
Although not readily observable in any occupied frontier molecular orbitals of the endo adduct, the LUMO+1 MOs showed a distinct difference in secondary orbital interactions, with the endo approach having a greater contribution to the overall MO from this and a slightly lower energy than the LUMO+1 for the exo approach.
MO analysis showed that only MOs with the same symmetry (with respect to the plane of symmetry) were able to combine, and this symmetry was preserved from this combination in the TS MOs. Here, even semi-empirical methods were adequate to demonstrate this phenomenon.
One might suggest that a higher level of theory might be used to try and quantify and highlight the small differences in energy between both the endo/exo transition states, and the endo/exo products. However this would be too computationally demmanding for a project of this timescale, and the simplicity of these reactions does not warrant such time intensive modelling.
References
- ↑ PAC, 1994, 66, 1077, DOI:10.1351/pac199466051077
- ↑ O. Wiest, K. A. Black, K. N. Houk, J. Am. Chem. Soc., 1994, 116, 10337 DOI:10.1021/ja00101a078
- ↑ R. B. Woodward, R. Hoffmann, J. Am. Chem. Soc., 1965, 87, 397 DOI:10.1021/ja01080a054
- ↑ Rzepa, 2nd Year Conformational Analysis, 2011
- ↑ G. Schultz, I. Hargittai, Journal of Molecular Structure, 1995, 346 (0), 63 DOI:*
- ↑ M. J. Goldstein, M. S. Benzon, J. Am. Chem. Soc., 1972, 94, 7149 DOI:10.1021/ja00775a046
- ↑ Clayden et al. Org. Chem, 2001 pp. 905-918
- ↑ McDaniel, K; Mathew Weekly, R; J. Chem Ed. Vol. 74 No. 12 1997; pp.1465-1467
- ↑ J. Breulet, H. F. S. III, J. Am. Chem. Soc., 1984, 106, 1226 DOI:10.1021/ja00317a009
- ↑ R. Hoffmann, R. B. Woodward, J. Am. Chem. Soc., 1965, 87, 4389 DOI:10.1021/ja00947a033