Rep:Mod:LS1109bananarama
Introduction
Quantum mechanical calculation methods used to predict/explain bonding/structure in inorganic compounds are explored in this module. DFT/B3LYP calculations are widely used in research[1] and will be explored extensively here. Throughout, Gaussian 09W was used to perform calculations. GaussView 5.09 was the graphical interface used to create/optimise molecules and display results produced by Gaussian 09W.
To optimise a molecule, the energy of the system is calculated by solving the Schrodinger equation under the Born Oppenheimer approximation for a given set of nuclear co-ordinates. The nuclear co-ordinates of the molecule may be represented by R, and the calculated energy of the molecule is E(R). If the nuclear co-ordinates are varied (R'), E(R') may be calculated. For every iteration, the absolute value of the rate of change of E(R) with respect to R (the Root Mean Squared (RMS) Gradient) is calculated. When the RMS Gradient is at zero, the potential energy curve of the system has zero gradient. Calculating the second derivative may be used to determine whether this point is the global minimum, a false minimum or a transition state.
The DFT (Density Functional Theory) B3LYP method is used throughout this project because of its excellent ability to combine a relatively high accuracy of prediction with low computational demmand.
Computational Molecular Orbital Analysis of BH3
Trigonal Planar BH3 was constructed in Gaussview 5.09, and bond lengths were set to 1.5Å. The molecule was subsequently optimised with the DFT/B3LYP method and primitive STO 3-21g basis set. This was sufficient for the purposes of this investigation as the BH3 molecule is small and highly symmetric, meaning its chemistry is likely to be easily predicted. Details from this optimisation are shown belowLOG FILE:
BH3 Optimisation File Name = BH3_OPT2 File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 3-21G Charge = 0 Spin = Singlet E(RB3LYP) = -26.46226338 Ha RMS Gradient Norm = 0.00020672 a.u. Imaginary Freq = - Dipole Moment = 0.0000 Debye Point Group = D3H Job cpu time: 0 days 0 hours 0 minutes 11.0 seconds.
This summary confirms the near-zero RMS gradient corresponding to a global minimum (or false minimum/transition state). The calculation method and basis set are described along with the computing time. This summary was used to confirm the job had taken place. The Dipole moment (0.0 Debeye) confirms the highly symmetrical nature of the molecule along with the D3h point group. The optimisation log file was analysed to confirm all parameters had converged:
Item Value Threshold Converged? Maximum Force 0.000090 0.000450 YES RMS Force 0.000045 0.000300 YES Maximum Displacement 0.000352 0.001800 YES RMS Displacement 0.000176 0.001200 YES Predicted change in Energy=-4.757210D-08 Optimization completed. -- Stationary point found.
It can be seen here that the RMS of the gradient is negligable (at less than 0.001) and therefore characteristic of an energy minimum. It is also noted that all parameters were determined to have converged successfully in 4 optimisation steps.
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- ------------------------
! Name Definition Value Derivative Info. !
------------------------------------------------------------------------------
! R1 R(1,2) 1.1945 -DE/DX = -0.0001 !
! R2 R(1,3) 1.1945 -DE/DX = -0.0001 !
! R3 R(1,4) 1.1945 -DE/DX = -0.0001 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
------------------------------------------------------------------------------
The calculated bond length (1.19Å), bond angle (120o), and point group were found to agree with literature[2] The 3D molecular structure may be found here ()
The plot (above) of energy versus optimisation number demonstrates four steps were needed to optimise BH3's geometry to find its minimum energy. The 1st derivative (RMS grad. norm) of energy with respect to the optimisation step number shows the 4th optimisation produced a small enough gradient to correspond to a minimum. It was deemed unecessary to
carry out further optimisation, especially as the data produced was concordant with literature.
Frequency Optimisation
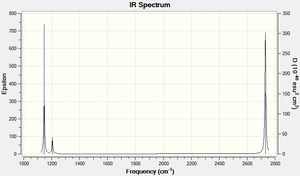
A frequency optimisation calculation was carried out on the optimised molecule LOG FILE. The frequency optimisation essentially produces the 2nd derivative of the potential energy surface and allows us to determine whether the optimised molecule was in the ground state or a transition state (where the RMS grad. is also zero). If the molecule was in a transition state, one of the calculated frequencies would be negative. If in the ground state, all frequencies would be positive (as is the case here).
Furthermore, this optimisation allows the peak abosorbance frequencies of all vibrational modes of BH3 to be predicted. The results confirm that due to the absence of low/negative absorption frequencies, the optimised structure was in-fact in its ground state (confirmed by comparing absorption frequencies to literature and the absence of negative frequencies):
| Vibrational Mode | Form of Vibration | Calculated Freq. [Literature] (cm-1) | Intensity | |
|---|---|---|---|---|
| A1' | Totally symmetric vibration: concerted, equal displacement of the H atoms from the equilibrium bonding distance (stretching/compression) Form of Vibration. Undetected in experimental IR because of an unchanged dipole moment associated with this vibration | 2592 [N/A] | [N/A] | |
| A2" | Out-of-plane wagging (Umbrealla Motion): The 3 H atoms move in the z axis (above and below the plane of the molecule) in equal amounts and in a concerted manner. The B atom moves in an opposited direction to the H atoms to preserve the molecule's centre of mass. Form of Vibration. | 1146 [1159] | 92.7 | |
| E' | In-plane scissoring: 2 H atoms come together/move away from each other in a scissoring motion. The remaining H atom and B atom 'recoil' in a concerted manner in the plane of the molecule at a smaller amplitude (to preserve the centre of mass). This results in two enlarged (factor n) H-B-H bond angles, and one H-B-H angle reduced (factor 2n) Form of Vibration. | 1205 [1202] | 12.4 | |
| E' | In-plane rocking: 2 H atoms and the B atom (BH2 unit) 'rock' in the plane of the molecule. The H-B-H bonding angle remains constant in this unit. The remaining H atom has an opposing (to the BH2 unit) rocking motion with a significantly larger displacement amplitude. This results in one H-B-H bonding angle being reduced and the other increased. Form of Vibration. | 1205 [1202] | 12.4 | |
| E' | Asymmetric Stretching: Two BH units contract and expand in an asymmetrical manner. The B atom wags in the plane of the molecule to oppose these motions and preserve the centre of mass. The remaining H atom is stationary. Form of Vibration. | 2730 [2506] | 103.9 | |
| E' | Asymmetric Stretching: Two H atoms move away from the B atom along their bonds in a concerted manner (amplitude of displacement n). The remaining H atom moves to compress its B-H bond (amplitude of displacement √3) Form of Vibration. | 2730 [2506] | 103.9 |
Figure 1: IR vibration modes of BH3
Although 6 vibrational modes are described above, only 3 exist in the spectrum. The A1' vibration is totally symmetric and its motion creates no dipole moment. It is therefore IR inactive (no peak at 2592cm-1). Additionally, the absorption at 1205cm-1 is the result of two degenerate vibrational modes (E'). This is also the case at 2731cm-1, where there are also degenerate vibrational modes (E').
It is commonly reported that high frequency absorption vibrational modes are modelled less accurately than lower frequency modes. This is again the case here, with the highest frequency absorption having an 8.98% error, whereas the lowest frequency absorption only had an error of 1.12%. The calculated vibrational mode with the smallest frequency percentage error was 0.25% (In-plane scissoring & rocking).
Molecular Orbital Analysis of BH3
A molecular orbital diagram was constructed through the use of the Klopman-Salem equation in a qualitative manner and an LCAO approach. The B 1s orbital was considered to be too low in energy to take part in any bonding interactions in the BH3 molecule.
The fragment orbitals of trigonal planar H3 were determined through application of the reduction and projection formulae from a reducable representation table of H3. Knowledge that Hydrogen and Boron are of similar electropositivity, and therefore energy, was taken into consideration when constructing the diagram.
It was relatively facile to predict the energy ordering of most of the BH3 symmetry derived MOs using LCAO due to the simplicity of the molecule. More difficult however was the prediction of the energy gaps between MOs. It is hard to accurately estimate these spacings, without a thorough quantitative analysis. Therefore computational analysis is likely to provide a better understanding of the reactivity of the molecule. A computational analysis is alsio likely to be significantly more useful when dealing with more complex molecules, where LCAO MOs are more difficult to construct/predict manually.
Analysis of the calculated MOs shows that the 1s AO does not in fact interact with the H atoms as predicted.
The energy ordering of the 1a1' MO up to the 1a2" MO was predicted correctly. However, the predicted order of the 2e' and 3a1' MOs was wrong. The 3a1' MO was found to be lower in energy than the 2e' MO.
One would expect that due to the greater overlap associated with s orbitals (compared to the s/p overlap) that the a1 antibonding orbital woud have a higher energy. However, it is difficult to estimate the interaction energy of these MOs. This prediction error however is not especially important, as the majority of the reactivity and chemistry associated with the BH3 molecule is explained through analysis of the HOMO and LUMO, whose energy ordering was predicted correctly.
The shapes of the DFT calculated MOs also show significant similarity in shape and relative contributions with what is predicted by the LCAO approach. This observation both highlights the accuracy of the computational method and that the LCAO approach is a good approximation at this level.
MO Energy (Ha) 1a1' -6.76 2a1' -0.515 1e' -0.353 1a2'' -0.0682 3a1' +0.165 2e' +0.179
The BH3 molecule was optimised with DFT/B3LYP, using the 3-21G basis set and full NBO/population analysis LOG FILE.
Charge Distribution and NBO analysis of BH3
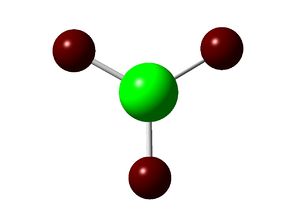
Below is the charge distribution of BH3 as calculated with DFT/B3LYP and the 3-21G basis set. The Boron atom is highly electron defficient (see table, Natural Charge = 0.331). This is logical, as BH3 is known to be a strong Lewis acid, with the Boron atom having an empty, low-lying pz orbital. As expected, the H atoms show equal charge distribution between them (Natural Charge = -0.110).
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
B 1 0.33121 1.99904 2.66976 0.00000 4.66879
H 2 -0.11040 0.00000 1.11008 0.00032 1.11040
H 3 -0.11040 0.00000 1.11008 0.00032 1.11040
H 4 -0.11040 0.00000 1.11008 0.00032 1.11040
=======================================================================
The data below is taken from the log file of the optimisation. It gives a description of the orbital contributions (s & p) of each MO (only the 8 lowest energy MOs are described below).
The first three NBOs involve Boron and an H atom. 45.4% of the bond contribution for each MO is from the B atom orbitals that are sp2 hybridised (33.33% s character, 66.67% p character). 54.6% of the bond contribution comes from H atom s-orbitals (s=100%) as expected.
The 4th NBO was predicted by LCAO to be the non-bonding pz orbital. NBO analysis contradicts this prediction. The NBO has been described as having 100% s-character. One would predict this MO to have 100% p-character due to the conventional description of bonding in BH3. This contradiction may be due to the somewhat-primitive nature of the basis set used. Alternatively, although the conventional description of bonding in BH3 is able to describe and predict the chemistry of the molecule, this may be purely coincidental and not actually representative of the bonding in the molecule.
Likewise, the 5th-8th NBOs give uncharacteristic orbital contributions to the NBOs. This may be due to their lack of occupancy rendering them uncharacterisable.
Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis does not suggest any significant second order orbital mixing in the BH3 molecule, which is to be expected for the highly symmetrical planar BH3 molecule.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.99852) BD ( 1) B 1 - H 2
( 45.37%) 0.6736* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.0000 0.0000
0.8165 0.0000 0.0000 0.0000
( 54.63%) 0.7391* H 2 s(100.00%)
1.0000 0.0001
2. (1.99852) BD ( 1) B 1 - H 3
( 45.37%) 0.6736* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 54.63%) 0.7391* H 3 s(100.00%)
1.0000 0.0001
3. (1.99852) BD ( 1) B 1 - H 4
( 45.37%) 0.6736* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 -0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 54.63%) 0.7391* H 4 s(100.00%)
1.0000 0.0001
4. (1.99954) CR ( 1) B 1 s(100.00%)
1.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000
5. (0.00000) LP*( 1) B 1 s(100.00%)
6. (0.00000) RY*( 1) B 1 s( 0.00%)p 1.00(100.00%)
7. (0.00000) RY*( 2) B 1 s( 0.00%)p 1.00(100.00%)
8. (0.00000) RY*( 3) B 1 s( 0.00%)p 1.00(100.00%)
.
Analysis of Thallium Tribromide

TlBr3 was optimised using the DFT/B3LYP method and the LANL2DZ basis set LOG FILE. The structure was constrained to the D3h point group to speed-up the calculation (there are 181 electrons in TlBr3) and avoid optimising the molecule to a transition state/false minimum. The summaries of this optimisation and the subsequent frequency optimisation are shown below.
The LANL2DZ basis set is a pseudo-potential and appreciates the relativistic effects not considered by the Schrodinger Equation, which are ecountered in larger atoms such as Br and Tl.
From the optimisation, the Tl-Br bond distance was determined to be 2.65Å, and the bonding angle 120o . This is concordant with literature[3] .
TlBr3_opt File Name = TLBR3_OPT File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -91.21812851 Ha RMS Gradient Norm = 0.00000088 a.u. Imaginary Freq = 0 Dipole Moment = 0.0000 Debye Point Group = D3H Job cpu time: 0 days 0 hours 0 minutes 6.0 seconds.
All parameters converged in this optimisation and a low RMS gradient was produced corresponding to the global minimum (confirmed through frequency analysis below):
Item Value Threshold Converged?
Maximum Force 0.000002 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000022 0.001800 YES
RMS Displacement 0.000011 0.001200 YES
Predicted change in Energy=-5.660842D-11
Optimization completed.
-- Stationary point found.
.
Frequency Analysis of TlBr3
TlBr3_opt_freq File Name = TLBR3_OPT2_FREQ File Type = .log Calculation Type = FREQ Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -91.21812851 Ha RMS Gradient Norm = 0.00000088 a.u. Imaginary Freq = 0 Dipole Moment = 0.0000 Debye Point Group = D3H Job cpu time: 0 days 0 hours 0 minutes 19.0 seconds.
As can be seen from the summaries above, the frequency optimisation proved that the global minimum had been found from the optimisation calculation. Below is a summary of the vibrational modes of TlBr3 LOG FILE:
| Vibrational Mode | Form of Vibration | Calculated Freq. (cm-1) | Intensity | |
|---|---|---|---|---|
| A1' | Totally symmetric vibration: concerted, equal displacement of the Br atoms from the equilibrium bonding distance (stretching/compression) Form of Vibration. Undetected in experimental IR because of an unchanged dipole moment associated with this vibration | 165 | [N/A] | |
| A2" | Out-of-plane wagging (Umbrealla Motion): The 3 Br atoms move in the z axis (above and below the plane of the molecule) in equal amounts and in a concerted manner. The Tl atom moves in an opposited direction to the Br atoms to preserve the molecule's centre of mass. Form of Vibration. | 52 | 5.85 | |
| E' | In-plane scissoring: 2 Br atoms come together/move away from each other in a scissoring motion. The remaining Br atom and Tl atom 'recoil' in a concerted manner in the plane of the molecule at a smaller amplitude (to preserve the centre of mass). This results in two enlarged (factor n) Br-Tl-Br bond angles, and one Br-Tl-Br angle reduced (factor 2n) Form of Vibration. | 46 | 3.69 | |
| E' | In-plane rocking: 2 Br atoms and the Tl atom (TlBr2 unit) 'rock' in the plane of the molecule. The Br-Tl-Br bonding angle remains constant in this unit. The remaining Br atom has an opposing (to the TlBr2 unit) rocking motion with a significantly larger displacement amplitude. This results in one Br-Tl-Br bonding angle being reduced and the other increased. Form of Vibration. | 46 | 3.69 | |
| E' | Asymmetric Stretching: Two TlBr bonds contract and expand in an asymmetrical manner. The Tl atom wags in the plane of the molecule to oppose these motions and preserve the centre of mass. The remaining Br atom is stationary. Form of Vibration. | 211 | 25.5 | |
| E' | Asymmetric Stretching: Two Br atoms move away from the Tl atom along their bonds in a concerted manner (amplitude of displacement n). The remaining Br atom moves to compress its Tl-Br bond (amplitude of displacement √3) Form of Vibration. | 211 | 25.5 |
Figure 2: IR vibration modes of TlBr3
The low frequencies (in cm-1) were found from the log file of the frequency optimisation calculation:
Low frequencies --- -3.4213 -0.0026 -0.0004 0.0015 3.9362 3.9362
The lowest 'real' vibrational mode of TlBr3 was determined to be 46cm-1. The lowest frequency was an order of magnitude smaller than this, and therefore the accuracy of the frequency optimisation calculation was deemed acceptable, and as no appreciable negative frequencies were found, as well as the molecule being strictly held to the D3h point group, the molecule was determined to have been optimised to its global minimum potential energy.
What is a bond?
A bond is a region where electron density is shared between valence orbitals of two (or more) nuclei that are close enough to experience a significant attractive interaction. The traditional depiction of a bond as a link between two atoms is sufficient to explain fundamental phenomena in chemistry. In some cases however, this depiction of a bond falls short and fails to explain reactivity and properties of molecules. It is often difficult to define when an attractive interaction becomes significant enough to be considered a bond between atoms.
Gaussview uses the distance between atoms to determine whether they are bonded. This often works well, but in truth is a poor choice of parameter to determine if a bond exists between nuclei. Although likely to be too computationally demmanding, a measure of the electron density between sets of atoms would be a much better determinant. A classic example of this interpretational limitation is GaussView's failure to allocate bonds between the P and Cl atoms of the PCl3 ligands in the Molybdenum complexes. GaussView is limited by its simplistic aproach to visually interpeting numerical data. It must therefore be noted that even if GaussView does not show a bond between atoms, there may still be a significant bonding interaction between these atoms.
Cis and trans isomerisation of Mo(CO)4L2
The differences in the IR spectra of cis/trans Mo(CO)4L2 were explored in the 2nd year synthesis labs. The Cis- isomer produced 4 IR CO absorption bands, whereas the trans- isomer only produced one.
It is impractical to model the molecule in question Mo(CO)4(PPh3)2 due to the large number of electrons in the bulky PPh3 ligands. This would make the calculations extremely computationally demanding.
A convenient solution to this problem is to model this molecule (using pseudo-potentials) using Cl atom substituents on the Phosphorous atom instead of phenyl molecules. Chlorine acts similarly in a steric and electronic manner to Ph, but is less computationally demanding (due to a smaller number of valence electrons). Therefore, cis/trans-[Mo(CO)4(PPh3)2] were modelled as cis/trans-[Mo(CO)4(PCl3)2].
Initially, the theoretical compounds were optimised 'loosely' to avoid optimisation to a local potential energy minimum using DFT/B3LYP and the LANL2MB basis set LOG cis form, LOG trans form .
The orientation of the Cl substituents in the PCl3 ligands was altered on advice from Dr Hunt (Dr Hunt had analysed the rotational energy potential profile of the molecule to determine a good starting orientation of the Cl atoms for optimisation.). The cis- isomer was optimised to the following configuration: with one Cl pointing up parallel to the axial bond, and one Cl on the other PCl3 group pointing down parallel to the axial bond; The tran-isomer was optimised so that both PCl3 ligands were eclipsed with one Cl from each ligand oriented parallel to a Mo-C bond:
| Cis Isomer | Trans Isomer (eclipsed PCl3 groups) |
|---|---|
|
|
Figure 3:
Cis Isomer File Name = checkpoint_47203 File Type = .fch Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2MB Charge = 0 Spin = Singlet Total Energy = -617.52510211 Ha RMS Gradient Norm = 0.00002360 a.u. Imaginary Freq = Dipole Moment = 8.6309 Debye Point Group = C2
Trans Isomer File Name = checkpoint_47257 File Type = .fch Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2MB Charge = 0 Spin = Singlet Total Energy = -617.52212411 Ha RMS Gradient Norm = 0.00007125 a.u. Imaginary Freq = Dipole Moment = 0.2842 Debye Point Group = CS
These optimisations using the LANL2MB basis set were built upon by further optimisation using the more complex and accurate LANL2DZ basis set in combination with ultrafine electronic convergence LOG cis form LOG trnas form. The LANL2DZ (DZ=double zeta) models each atomic orbital in the molecule with two Slater Type Orbitals. This will give a much better description of the valence atomic orbitals, and therefore a more accurate prediction of the bonding in the isomers.
Further to this, due to Phosphorous' tendency to make use of its low-lying d-orbitals, the gaussian input file was modified manually to add a D orbital function to the basis set LOG cis form LOG trans form:
Cis Isomer File Name = checkpoint_47228 File Type = .fch Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet Total Energy = -623.57707183 Ha RMS Gradient Norm = 0.00001711 a.u. Imaginary Freq = Dipole Moment = 1.3097 Debye Point Group = C2 Cis Isomer with consideration of the D AOs File Name = log_47383 File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -623.69291226 a.u. RMS Gradient Norm = 0.00001133 a.u. Imaginary Freq = Dipole Moment = 0.0762 Debye Point Group = C1 Job cpu time: 0 days 1 hours 1 minutes 14.0 seconds.
Trans Isomer File Name = checkpoint_47229 File Type = .fch Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet Total Energy = -623.57603111 Ha RMS Gradient Norm = 0.00000124 a.u. Imaginary Freq = Dipole Moment = 0.3043 Debye Point Group = Cs Trans Isomer with consideration of D AOs File Name = log_47384 File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -623.69415609 Ha RMS Gradient Norm = 0.00000125 a.u. Imaginary Freq = Dipole Moment = 0.2293 Debye Point Group = C1 Job cpu time: 0 days 1 hours 17 minutes 4.3 seconds.
No negative frequencies were observed in either isomer, confirming optimisation of the compound to a global minimum. The energies (reported in Hartrees above) were compared to determine which isomer was lower in energy.
Using the LANL2MB basis set with loose optimisation, the cis isomer (-617.525Ha) was 7.82kJmol-1 lower in energy than the trans isomer (-617.522Ha). Using the LANL2DZ basis set with ultrafine electronic convergence, the cis isomer (-623.577Ha) was 2.73kJmol-1 lower in energy than the trans isomer (-623.576Ha). Using the LANL2DZ basis set with the adapted basis set the cis isomer (-623.693Ha) was 3.27kJmol-1 higher in energy than the trans isomer (-623.694Ha). This is a fairly small energy difference, however, it is reported in literature that the cis-form (with PPh3 ligands)slowly isomerises to the trans form at room temperature, confirming these results. As the energy gap is small in this theoretial optimisation, it is likely that a larger energy gap is present experimentally, with the interconversion likely to be solvent mediated, and the bulky phenyl groups playing a greater role in sterics terms.
Because of the superior accuracy of the adulterated basis set optimisation, it may be assumed that the trans- isomer is in fact the more stable isomer, as it is likely there is some participation of D AOs in the bonding of Phosphorous, which the unadulterated basis sets are not able to reflect in their optimisations.
Frequency Analysis of Mo(CO)4(PCl3)2
Low Frequency Vibrations
When analysed, the low frequency vibrations showed various stretching modes of the large, heavy PCl3, which explains the low frequency of these vibrations. They also have low intensity due to their symmetrical nature: LOG cis form freq. LOG trans form freq..
All these low frequency vibrations involved rotations around the Mo-P bonds, whose large substituents are reflected in their low wavenumbers. At room temperature, the energy of the surroundings far exceeds the energy required for these vibrations/rotations, and they may therefore be considered to occur spontaneously (e.g. Mo-P bond rotation occurs readily). This observation explains the incorrect point group assignment of the cis- and trans-forms, as Gaussian does not consider free rotation of these Mo- bonds, leading to the loss in symmetry observed for the theoretical molecules.
| Calculated Freq. (cm-1) (Trans) | Intensity (Trans) | Animation (Trans) | Calculated Freq. (cm-1) (Cis) | Intensity (Cis) | Animation (Cis) | |
|---|---|---|---|---|---|---|
| 5 | 0.09 |  |
11 | 0.03 | 
| |
| 6 | 0 |  |
18 | 0.007 | 
| |
| 37 | 0.419 |  |
42 | 0 | 
|
| Cis Isomer | Trans Isomer |
|---|---|
|
|
Figure 4: The pre-optimised orientations of the Molybdenum isomers
Carbonyl Stretching Region IR Analysis
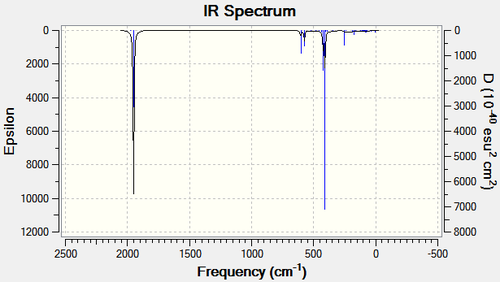
Close inspection of the carbonyl stretching region in the cis- isomer reveals 4 vibratonal modes at 1945cm-1 (b2), 1949cm-1 (b2), 1958cm-1 (a1) and 2023cm-1 (a1): more than the trans isomer.
This is expected due to the reduced symmetry of the cis- isomer. These values were in rough agreement with literature for cis-[Mo(CO)4(PCl3)2].[4]
The trans two absorptins in the CO stretching range which were predicted to be degenerate due to the molecules symmetrical nature. Two other absoprtions were observed in minimal/zero intensity absorptions.
| Vibrational Mode | Calculated Freq. (cm-1) | Intensity | Lit. cis-[Mo(CO)4(PCl3)2] (cm-1). | Lit. cis-[Mo(CO)4(PPh3)2 (cm-1) | |
|---|---|---|---|---|---|
| b2' | 1945 | 165 | 1986 | 1897 | |
| b2" | 1949 | 165 | 1994 | 1907 | |
| a1' | 1958 | 165 | 2004 | 1927 | |
| a1' | 2023 | 165 | 2072 | 2023 |
Figure 5: IR vibration modes of cis-[Mo(CO)4(PPh3)2
| Vibrational Mode | Calculated Freq. (cm-1) | Intensity | Lit. cis-[Mo(CO)4(PCl3)2 (cm-1). | Lit. cis-[Mo(CO)4(PPh3)2 (cm-1) | |
|---|---|---|---|---|---|
| Eu | 1950 | 1475 | 1896 | 1902 | |
| Eu | 1950 | 1467 | 1896 | 1908 | |
| B1g | 1977 | 0.65 | [N/A] | [N/A] | |
| Alg | 2031 | 3.8 | [N/A] | [N/A] |
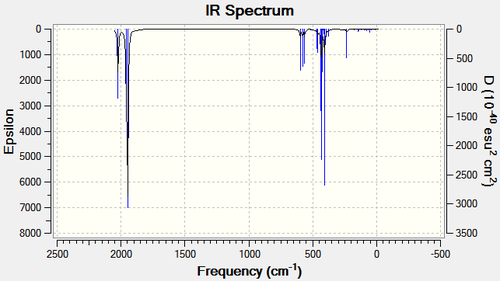
Figure 6: IR vibration modes of trans-[Mo(CO)4(PPh3)2
Vibrations of the trans form are in rough agreement with the experimentally determined IR spectra. The B1g and A1g vibrations are IR inactive and this corresponds with their low observed frequency. The two Eu vibrational modes are calculated to be not quite degenerate and therefore slightly disagree with literature.
In order to confirm the reliability of the optimisations, bond angles and bond lengths of the isomers were compared to literature[5][6] of similar Molybdenum complexes.
Bond distances were found to be in close agreement with literature values of similar complexes.
It is interesting to note the Mo-P bond length differences between the cis- and trans- isomers. The Mo-P bond in the cis isomer is longer. This is probably a result of bulky Cl (or Ph3) groups (which are in close proximity to those on the other Phosphorous ligand) in the cis- form, increasing the Mo-P bond distance to reduce steric strain. This steric strain may also be a significant contributing factor to the increased stability of the trans- form.
Furthermore, one may consider a trans- effect to exist in the cis- isomer, with the carbonyl groups trans to the PCl3 group having shorter Mo-C bond distances than those cis- to the Phosphorous ligand, or those in the trans- isomer.[7]
This phenomenon arises from the donation of the trans- phosphorous ligand's lone pair to the metal, causing increased electron density donation to the π-acceptor trans- carbonyl ligand, thus decreasing the Mo-C bond distance relative to the cis- ligand, where this is less effectively experienced. Mo-C bond lengths were shown to be 0.05Å shorter in the CO ligands trans to the PCl3 group.
Considering the P-Mo-P bonding angle in the cis- isomer, the optimised value with the adulterated basis set was calculated as 92.3o. Literature however reported this angle (for the PPh3 complex) at 104.6o. This demonstrates the limitations of substituting the phenyl groups for Cl atoms, especially when considering absolute steric effects.
Cis- Isomer Bond Type Bond Length Cis to P [Lit.] (Å) Bond Length Trans to P [Lit.] (Å) Mo-C 2.06 [1.97] 2.01 [2.06] C=O 1.17 [1.16] 1.18 [1.13] P-Cl 2.24 [??] Mo-P 2.51 [2.58] Trans- Isomer Bond Type Bond Length [Lit.] (Å) Mo-C 2.06 [2.01] C=O 1.17 [1.17] P-Cl 2.24 [??] Mo-P 2.44 [2.50]
Altering the relative stability of the cis- and trans- isomers in Mo(CO)4PR3
It is demonstrated that in Mo(CO)4PR3 where R=Cl/Ph, there were steric repulsions between the PR3 ligands causing the P-Mo-P bond angle to exceed the 90o angle that is conventional with octahedral complexes.
By manipulating the phosphorous ligand substituents to create an attractive force between them intead of a repulsive one, one may lower the energy of the cis- isomer. With correct manipulation, the relative stabilities of the isomers may be reversed. This could have use in catalytic chemistry for example, for a catalytic process where the cis- isomer displays exclusive catalytic activity.
One possible approach is to functionalise the phosphorous atoms with hydroxide groups. When in the cis- form, hydrogen bonding between hydroxide groups would further stabilise this isomer, and could also reduce the P-Mo-P bonding angle below 90o, which would allow more space for other ligands.
Cis-[Mo(CO)4(P(OH)3)2] LOG
File Name = checkpoint_47415 File Type = .fch Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ with extra basis set Charge = 0 Spin = Singlet Total Energy = -989.06103805 Ha. RMS Gradient Norm = 0.00000639 a.u. Imaginary Freq = Dipole Moment = 5.1195 Debye Point Group =
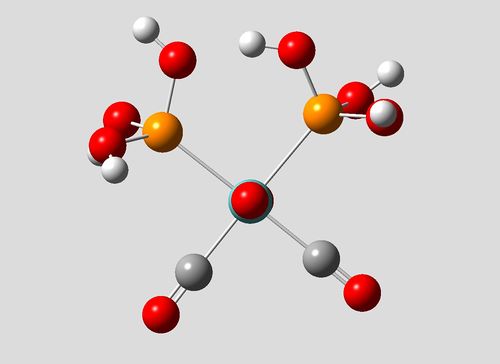
| Cis Isomer | Cut-away view of HOMO showing H-bonding between OH groups |
|---|---|
|
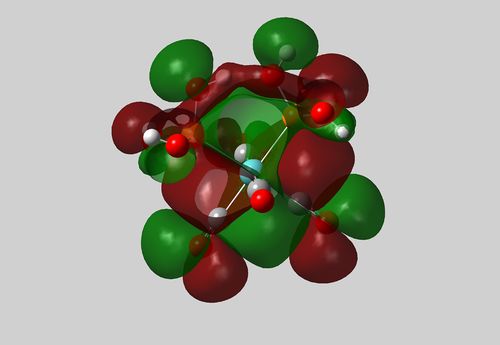
|
Figure 7:
Trans-[Mo(CO)4(P(OH)3)2] LOG
File Name = oh trans File Type = .fch Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ with extra basis set Charge = 0 Spin = Singlet Total Energy = -989.04772325 Ha RMS Gradient Norm = 0.00000133 a.u. Imaginary Freq = Dipole Moment = 1.5802 Debye Point Group =
It is shown from the summary files and subsequent conversion of energy values, that the cis- form of this complex is in fact 35.0kJmol-1 lower in energy than the trans form. The cis- forms increased stability may be attributed to hydrogen bonding between the OH groups in the cis phosphorous ligands, and an increased trans-effect due to the now the electron rich OH substituents on the phosphorous atom. A hydrogen bonding interaction is shown in the HOMO (also present in lower energy MOs) in the cutaway image above.
Mini Project: Bonding in Hypervalent Phosphorous-Halide Molecules
Phosphorous halides are well reported in literature as being able to exist as hypervalent penta- (PX5) or hexa- (PX6-) coordinated compounds.[8]. Pentahalide compounds are also reported to have a hybrid of ionic and covalent bonding character, which is highly dependant on the halide in question.[9] Literature has suggested that in PF5, the preference of Phosphorous to not exceed the octet rule, leads to a degree of ionic bonding of axial F atoms.[10]. In this Mini-Project, the chemistry of hypervalent Phosphrous Fluoride and Phosphorous Chloride molecules will be examined.
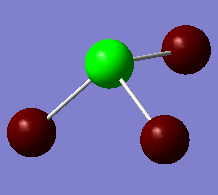
Both PF3 and PCl3 are described as volatile, reactive compounds that take a pyramidal geometry with phosphorous adopting sp3 hybrid orbitals. The lone pair on the P atom is in an sp3 hybrid. PCl3 is readily oxidised to PCl5, and is considered to be more reactive than PF3, leading to its wide use as a synthetic reagent and precursor.
PF3 has a trigonal pyramidal geometry, with the lone pair pointing up the z-axis (C3v point group). In comparison to PCl3 it is relatively unreactive.
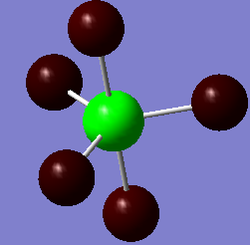
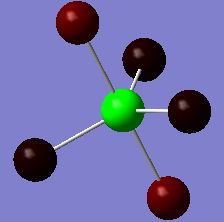
Phosphorous pentafluoride (PF5) is a mild Lewis acid (an F- acceptor) and is relatively chemically reactive. P-F bond lengths are observed on the NMR timescale as equal, due to a rapid interchange of the F ligands between axial and equatiorial positions via the Berry Mechanism.[8]. However, the axial P-F bonds have been shown to be longer than their equatorial equivalents. This effect is also observed in PCl5 It exists as the molecular PF5 form in all states. PF5 belongs to the D3h point group an is trigonal bipyramidal in nature.
PF5's hypervalent nature may be attributed to its use of low-lying d AOs to form sp3d hybrids.[11].
The phosphrous chlorides, PCl3 and PCl5 are more reactive than their fluroide equivalents, and are used to make the fluorides through halogen exchange.[12]. They belong to the same point groups and have the same symmetries.
PCl5 is reported to adopt a molecular geometry in the gas phase, an ionic form in the solid phase (as the PCl4+ / PCl6- ionic pairing), and can adopt either form in solution as well as a second ionic pairing (PCl5/PCl4+Cl-).
This mini-project aims to:
1. Establish the relative stabilities of PCl5 verus PCl3, and PF5 versus PF3.
2. Investigate the contributions of phosphorous low-lying d AOs to the bonding in PX5 molecules to create sp3d hybrid AOs through NBO analyis.
3. Compare axial vs. equatorial P-X bond distances, which are observed to be equivalent due to rapid interchange through the Berry Mechanism.
4. Examine the MOs of PF5 and PF3 (which will be similar to those for PCl5 and PCl3, but easier to model).
All molecules were optimised with the DFT/B3LYP method and 6-311G (d,p) basis set. An extra basis set for the dAOs was used with Phosphorous-containing molecules. All molecules were optimised with an ultrafine electronic convergence.
Table of Properties for PF3Lit. LOG, PF5 LOG, PCl3 LOG and PCl5 LOG:
| Molecule | P-F Bond Length [Lit.] (Å) | F-P-F Bond Angle (o [Lit.] | Dipole Moment (Debye) | Energy (Ha) | Point Group |
| PF3 | 1.60 [1.57] | 97.5 [97.8] | 1.55 | -641.07 | C3v |
| PF5 | 1.60(ax) [1.58], 1.57(eq) [1.53] | 90(ax/eq) [90], 120(eq/eq) [120] | 0 | -840.85 | D3h |
| PCl3 | 2.10 [2.04] | 101 [100] | 1.17 | -1722.10 | C3v |
| PCl5 | 2.19(ax) [2.12], 2.07(eq) [2.02] | 90(ax/eq) [90], 120(eq/eq) [120] | 0 | -2642.51 | D3h |
The calculated results show a strong concordance with literature, suggesting the inclusion of the extra basis set to describe the Phosphorous d AOs was necessary to obtain accurate geometric properties. The inequivalence of the axial and equatorial P-X bonds was observed in the PX5 compounds. In both cases, the hypervalent PX5 molecule was found to be more stable than PX3.
Natural Bond Analysis
Figure 8: Charge Distribution of Phosphorous Halides
It can be seen from the Natural Charge values (and visual representations) above, that Fluorine's high electronegativity causes a large electron defficiency on the phosphorous atom in both PF3 and PF5. Chlorine's reduced electronegativity in comparison is also reflected, with the natural charge on the P atom smaller compared to the fluoride equivalents. This is due to electron shielding (Cl has more shells than F) reducing the effective nuclear attraction of Chlorine.
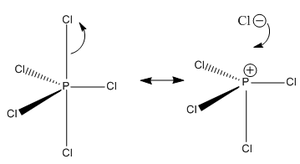
What is also interesting to note is the pronounced difference in natural charge present on the axial F/Cl atoms compared to their equatorial equivalents. Considerably more natural charge is held on the equatorial halide atoms. This is especially pronounced for PCl5, suggesting that sterics plays a part in this observation. The Cl atoms are very large in comparison to F atoms, and as a result axial P-Cl bond lengths are much larger than the equatorial P-Cl bond length (2.19Å vs. 2.07Å). This is further reflected in the accumulation of natural charge on the axial Cl atoms. One may also rationalise the increased ionic nature of the P-Cl bonds reported in literature which give rise to equilibria between PCl5 and ionic pairs. The axial P-Cl bonds are longer and more likely to dissociate to PCl4+Cl- for example:
This analysis is also able to explain PCl3's increased reactivity compared to PF3 - the sp3 hybridised lone pair in PCl3 is more readily available than in PF3 (PPCl3 = +0.769 versus PPF3 = +1.66) due to the decreased electron defficiency in PCl3. The increased availability of PCl3's lone pair increases its reactivity with respect to PF3.
On a related note however, it is easy to rationalise both the desire of PF3 and PCl3 to increase their coordination to PX5. Both molecules have strongly lewis acidic P atoms with a high natural charge (electron defficiency), a relatively spacious geometry, and low-lying D AOs, making them ideal targets for increased coordination to the P atom. This is demonstrated through the significantly lower energies of PF5/PCl5 versus PF3/PCl3 (-1722Ha/-2643Ha versus -641Ha/-841Ha).
Molecular Orbital Analysis of PF3
As demonstrated left, the Frontier Molecular Orbitals of PF3 were found to be suprisingly complex and unpredictable through a standard LCAO approach due to their highly complex nature in parts and unorthodox alignment and mixing.
Although difficult to predict, many of these frontier MOs and lower-lying MOs may be rationalised through chemical intuition and consideration of their energies and symmetries
LUMO: The LUMO was found to be doubly degenerate by DFT calculation. LCAO is able to rationalise these MOs to an extent. The doubly degenerate phosporus 3px and 3py AOs, which have e' symmetry are shown in LUMO(1) (with 3px) to interact with two F 2pz AOs and one 2px AO in what seems a largely antibonding/nonbonding interaction. The symmetry of the F3 fragment is difficult to determine and is not what is predicted by LCAO. It is therefore difficult to further rationalise this orbital without calculating the irreducible representation of the F3 FAO, which would be too time consuming given the length of this project. Suprisingly this MO was determined to be overall bonding (just) with an energy of -0.0241Ha. LUMO(2) shows a direct overlap of the P 3py) with an F 2pz AO. This is again not what LCAO would predict. Interesting to note is the complete envelopment of this 2pz AO. It is suprising that this MO has enough bonding character to be considered overall bonding. However closer inspection does show small bonding interactions of all F 2p AOs with the P 3py (most apparent in red). Decreasing the isovalue of this MO shows makes this observation more apparent.
HOMO: Conventional analysis would predict an sp3 hybridised lone pair HOMO. This is far from the case predicted by DFT, which shows an interaction of what is presumed to be Fluorine 3pz AOs and a highly displaced, warped P 3s orbital. Although this interaction looks highly antibonding, DFT has determined it to be bonding with an energy of -0.338Ha.
HOMO-1: One would consider this MO to be a largely non-bonding/antibonding F3 fragment that does not interact with any P AOs. It is therefore suprising that this MO is considered overall bonding at -0.438Ha. Decreasing the isovalue of this MO did not reveal any contribution from a P AO, but revealed the importance of the F3 fragment as a contribution to the overall bonding of the molecule. It is logical that there is no P AO that has this symmetry, but makes the overall bonding nature of this MO hard to rationalise.
HOMO-2: Again, these F3 fragments irreducible representations would be time consuming to determine. However, it is interesting to note a degree of mixing between F 2p AOs of different alignment. This is not predictable through a standard LCAO approach and builds upon the idea that bonding interactions within the F3 fragment are responsible for a significant degree of stability of the molecule. What is also interesting is the double degeneracy of this energy level. This is understandable as one would expect F3 fragment orbitals to show degeneracy, which is demonstrated here. Although not shown to be directly bonding with the P atom, bonding interactions with each other provide an overall bonding energy at -0.451Ha.
Degenerate MOs arising from degenerate P AOs and F Fragment orbitals are seen in lower energy MOs. The HOMO down to the HOMO-3 looks suprisingly antibonding in nature but have negative energies. Decreasing the isovalues of these MOs showed an envelopment of the molecule by these orbitals, with nodes being found where bonding interactions are expected between the P and F atoms.
When looking at the lowest energy MO, the isovalue had to be reduced to make the orbitals visible. This is rational, as this MO is so tightly held to the nucleus and low in energy (-77.2Ha) that it would be tiny in comparison to the more diffuse HOMO and LUMO. MO 1 at an isovalue of 0.0001 (normally 0.02) shows a 1s orbital on the P atom. This is logical as the nuclear attraction of the P atom at this distance is vast, and the 1s orbital is conventionally considered to be too low in energy to interact with F atoms.
Next, MO 2 was the F3 1s a1 symmetry fragment, which was minimally lower than the doubly degenerate e' F3 fragment AOs (MO 3 & MO 4) (0.00002Ha lower in energy). This may be explained by the fact these orbitals are so closely held to their respective nuclei that little or no interactions between them are observed.
MOs 5, 6, 7 & 8 were the P 2s, and 2p AOs which are again to low in energy to interact. The 2s AO was approximately 2Ha lower in energy than the 2p AOs (approximately -6Ha vs. -4Ha), but there was minimal difference between the 2p AOs, with the 2pz AO being minimally higher in energy than the doubly degenerate 2px and 2py AOs.
As LCAO would predict, there is little/no interaction between non valence AOs which occupy the lower energy levels. The first totally bonding MO is MO 9 at -1.28Ha (the conventional prediction of bonding between P and F as through electron density between the atoms).
It is much more difficult to rationalise the MOs of PF5 due to its increased complexity. Nonetheless, below the HOMO, F5 fragment orbitals are observed. Most interesting are the HOMO-1 and the doubly degenerate HOMO-2 energy levels shown to the left, which show the different fragment orbitals of the molecule, some of which are degenerate (e.g. HOMO-2).
A conventional approach to PF5 bonding predicts the use of sp3d hybrid orbitals to accomodate electron density beteen P and the 5 F atoms. This is clearly not the case in the MOs here, suggesting the concept of orbital hybridisation is far from what is actually observed, and is just an incorrect (although convenient) simplification of bonding.
One may hypothesise that a significant contribution to the overall stability of the molecule is the interaction of the F atoms with each other, enveloping the P atom and binding the molecule together. This hypothesis is founded from looking at the HOMO down to the HOMO-3 which shows all contributions to be coming from the F atoms. It is observed however that at lower MO energy levels, the conventional understanding of bonding as shared electron density between P and F atoms is observed (e.g. MO 11).
As for PF3 the lowest lying MO is the P 1s AO. Inspection of MOs 2-6 suggest a seperate F2 and F3 fragment. As for PF3, MO 2 was the a1 F3 fragment and MOs 3 & 4 were the doubly degenerate e' F3 AOs. Again, there was minimal energy difference between them. MOs 5 & 6 were the doubly degenerate axial F2 fragments. Again, none of the lower lying orbitals showed any significant interaction between them. MO 1 (-77.3Ha) was similar in energy to the PF3 MO 1 which is logical as there is no expected interaction. The first totally bonding interaction is observed in MO 11, which is suprisingly low-lying in energy.
Examination of the MO contributions from s, p and d AOs showed there to be no contributions from d AOs in phosphorous, suggesting the idea of sp3d hybrid orbitals is wrong. This is further backed up the the inequivalence of the axial and equatorial P-X bonds. The bonding picture of the pentahalides molecules is much more complex and will not be explored here.
Looking at the Bond orbital/Coefficients/Analysis section for PF5 is also interesting and disproves the conventional picture of bonding in PF5.
It can be seen that MOs 26-30 (HOMO-4 to the HOMO) are dominated by F lone pairs. This ties in with the idea of ionic bonding of some F atoms to maintain the octet rule in the P atom.
A conventional picture of this bonding would assume P needs 3 electrons (e.g. three covalently bonded F atoms (e.g. the planar F atoms)) to fill its shell. The axial F atoms were shown to have longer bonds, suggesting (with the observation of F p-lone pairs in HOMO to HOMO-4) more ionic character of the axial P-F bonds, with more electron density sitting on the F atoms:
Extract from the NBO Analysis of PF5
26. (1.97019) LP ( 2) F 5 s( 0.00%)p 1.00( 99.97%)d 0.00( 0.03%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.9998 0.0018 -0.0002 0.0000 -0.0090
0.0155 0.0000 0.0000
27. (1.92073) LP ( 3) F 5 s( 0.00%)p 1.00( 99.97%)d 0.00( 0.03%)
0.0000 0.0000 0.0000 0.0000 0.8659
0.0052 -0.0002 0.4999 0.0030 -0.0001
0.0000 0.0000 0.0000 0.0093 0.0000
0.0000 -0.0161 0.0000
28. (1.99067) LP ( 1) F 6 s( 76.94%)p 0.30( 23.06%)d 0.00( 0.00%)
-0.0002 0.8772 -0.0020 -0.0001 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
-0.4801 0.0066 -0.0033 0.0000 0.0000
0.0000 0.0000 -0.0064
29. (1.95808) LP ( 2) F 6 s( 0.00%)p 1.00( 99.97%)d 0.00( 0.03%)
0.0000 0.0000 0.0000 0.0000 0.9999
0.0038 -0.0001 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0168
0.0000 0.0003 0.0000
30. (1.95808) LP ( 3) F 6 s( 0.00%)p 1.00( 99.97%)d 0.00( 0.03%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.9999 0.0038 -0.0001
0.0000 0.0000 0.0000 -0.0003 0.0000
0.0168 0.0000 0.0000
.
Frequency Analysis of PF3 & Other Molecules
All Phosphorous halide molecules were confirmed to be minimal using frequency optimisation, which gave no appreciable negative or zero frequencies. PF3 Freq. PF5 freq. PCl3 freq. and PCl5 Freq.
The infra red spectrum of PF3 was determined through frequency optimisation with DFT/B3LYP and the 6-311g (d,p) basis set with ultrafine electronic convergence and a full nbo analysis. PF3's IR spectrum would be similar to that of PCl3, but the PCl3 wavenumbers would be lower due to the larger Cl atoms. PF5/PCl5 were not used due to their highly symmetric D3h point group. Due to its C3v point group, all vibrational modes of PF3 are IR active LOG Freq.
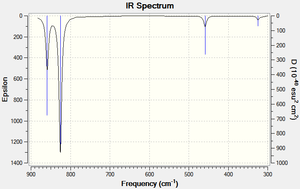
| Vibrational Mode | Form of Vibration | Calculated Freq. (cm-1) | Intensity | |
|---|---|---|---|---|
| E' | Scissoring: 2 F atoms come together/move away from each other in a scissoring motion. The remaining F atom and P atom 'recoil' in a concerted manner at a smaller amplitude (to preserve the centre of mass). This results in two enlarged (factor n) F-P-F bond angles, and one F-P-F angle reduced (factor 2n) Form of Vibration. | 324 | 5.67 | |
| E" | Rocking: 2 F atoms and the P atom (PF2 unit) 'rock' perpendicular to the z axis. The F-P-F bonding angle remains constant in this unit. The remaining F atom has an opposing (to the PF2 unit) rocking motion with a significantly larger displacement amplitude. This results in one F-P-F bonding angle being reduced and the other increased.Form of Vibration. | 324 | 5.67 | |
| A1' | Scissoring: All 3 F atoms come together/move away from each other in a scissoring motion. This results in the P atom being pushed up/down in the direction of the z-axis. Form of Vibration. | 459 | 30.0 | |
| E' | Asymmetric Stretching: One F atom and the P atom stretch/compress strongly, with the remaining 2 F atoms recoiling to preserve the centre of mass Form of Vibration. | 826 | 189 | |
| E' | Asymmetric Stretching: Two F atoms undergo an asymmetric stretch, with the P atom counteracting this motion by moving perpendicular to the z axis to preserve the centre of mass. The remaining F atom has a fixed position. Form of Vibration. | 826 | 189 | |
| A1' | Scissoring: All three F atoms move away from the P centre whilst the P atom moves away from the F atoms along the z axis. Form of Vibration. | 859 | 145 |
Figure 9: IR vibration modes of PF3
No credible literature was found to compare the experimental results with, but the number of observed peaks was in concordance with the IR spectrum of NH3[13], a symmetrically comparable molecule with C3v symmetry. Nonetheless, no negative frequency values of significant value were found in the log file or were present in the IR spectrum confirming the PF3 molecule had been optimised to a global minimum. Only 4 peaks were observed due to the degenerate nature of the E vibrational modes at 826cm-1 and 324cm-1.
Conclusion to Mini Project
The DFT/B3LYP method and 6-311G (d,p) basis set with an extra basis set to describe the contributions of the P D AOs, were used throughout this mini project to predict the chemistry of Phosphorous trihalides and pentahalides.
The trihalides were determined to be less stable than the pentahalides in accordance with observed reactivity. The relative stabilities of PCl3 and PF5 were justified by considering the charge distribution on the phosphorous and subsequently the availability of the sp3 hybridised P lone pair due to the differences in electronegativity between F and Cl.
Analysis of the bond lengths and bond angles of the pentahalides on the whole was concordant with literature. In combination with natural bond analysis, the sometimes ionic nature of PCl5 was able to be explained due to much longer axial P-Cl bonds, thought to be a result of the bulky nature of the Cl atoms.
The symmetry of the trihalides and pentahalides was correctly established as C3v and D3h. Furthermore, there was determined to be no contribution of d AOs to any bonding orbitals of PF5 (and this is assumed for PCl5 also), suggesting the sp3 d hybrid orbital approach to the bonding in PX5 molecules is unsubstantiated. This is further demonstrated through the inequivalence of axial and equatorial P-X bonds, and serves to increase the credibility of a partially ionic method of bonding in these molecules to avoid/reduce the breaching of the octet rule.
Analysis of the PF3 and PF5 molecular orbitals was difficult to approach due to the complex nature of the bonding interactions, but could generally be rationalised by chemical intuition and consideration of the atomic orbital contributions from each atom. LCAO would have been tremendously difficult and DFT modelling of these MOs seems the only comprehensive way of MO analysis, as although often easy to rationalise, the majority of the MOs and mixing present in them could not have been predicted. PCl3 and PCl5 woukd have had similar molecular orbital contributions and were therefore not modelled.
The conventional approach of sp3d hybridisation in PF5 and PCl5 seemed to be wrong, with the idea of an ionic component of the axial P-X bonds (with electron density held on the X atoms as lone pairs) having more credibility as these effects are observed in literature, especially with PCl5 being able to form ionic pairings.
This would be something to investigate further through the use of more accurate basis sets, but is beyond the scope of this project.
Conclusion
DFT/B3LYP calculations were used throughout this module with suprising success in predicting the chemistry of various molecules. Basis sets such as 3-21G were incredibly accurate at times given their tremendously primitive and approximate nature. However, molecules calculated by such methods were invariably very small and highly symmetrical, decreasing room for error.
The importance and convenience of pseudo-potentials was acknowledged through its ability to consider relativistic effects not taken into account by the schroedinger equation and reduce computational cost. Again, calculated geometric values showed little variation to literature.
Frequency analysis was used throughout the module to investigate vibrational modes and symmetries of molecules, as well as confirming the optimisation of these molecules to global minima and is invaluable as a verification tool in computational chemistry. IR spectra were often concordant with literature. Such optimisation techniques are increasingly being used as a tool for comparison and verification, and remove the need for expensive and time-consuming methods of obtaining these results (e.g. wet-lab work).
NBO analysis was useful in determining the relative contributions of atoms to a molecular orbital, although some predictions were not in agreement with the conventional understanding of molecular orbitals (e.g. the LUMO in BH3). Nonetheless, NBO was very useful in explaining the reactivity and chemistry of phosphorous halides in the mini-project. It builds upon the idea that a conventional approach to bonding is highly inadequate the more complex the molecule becomes, where its limitations become increasingly apparent.
Computational is a rapidly growing area of chemistry and is the future of the subject. Its value as an accurate technique for predicting the chemistry of molecules is unrivalled. It has been demonstrated in this module that even primitive calculation methods are able to produce results which are in agreement with what is observed experimentally. More complex and demmanding calculation methods are available and many more are being developed, suggesting an exciting future for this area.
References
- ↑ K. Burke, J. Werschnik and E.K.U. Gross, Journal of Chemical Physics 2005, 123, 123-131 DOI:10.1063/1.1904586
- ↑ M. S. Schuurman, W. D. Allen, H. F. Schaefer, Journal of Computational Chemistry, 2005, 26, 1106 DOI:10.1002/jcc.20238
- ↑ M. Atanasov, D. Reinen, J. Phys. Chem. A, 2001, 105, 5467 DOI:10.1021/jp004511j
- ↑ Elmer C et Al., Inorg. Chem., 1995, 34, pp.3864-3873
- ↑ G. Hogarth, T. Norman, Inorganica Chimica Acta, 1997, 254 (1), 167 DOI:*
- ↑ F. A. Cotton, D. J. Darensbourg, S. Klein, B. W. S. Kolthammer, Inorg. Chem., 1982, 21, 299 DOI:10.1021/ic00131a055
- ↑ B. J. Coe, S. J. Glenwright, Coordination Chemistry Reviews, 2000, 203 (1), 5
- ↑ 8.0 8.1 Gutowsky, H. S.; McCall, D. W.; Slichter, C. P., JJ. Chem. Phys., 1953, 21, 279 DOI:10.1063/1.1698874
- ↑ N. N. Greenwood & A. Earnshaw, Chemistry of the Elements (2nd ed.), Butterworth-Heinemann, Oxford, 1997
- ↑ G. Hogarth, T. Norman, Inorganica Chimica Acta, 1997, 254 (1), 167 DOI:*
- ↑ W. Kutzelnigg, Angewandte Chemie International Edition in English, 1984, 23, 272 DOI:10.1002/anie.198402721
- ↑ J. C. Lockhart, Chem. Rev., 1965, 65, 151 DOI:10.1021/cr60233a004
- ↑ Y. Yamaguchi, M. Frisch, J. Gaw, H. F. Schaeffer and J. S. Brinkley, J. Chem. Phys. 84, 2262 (1986).