Rep:Mod:LOTR3
The Cope Rearrangement Tutorial
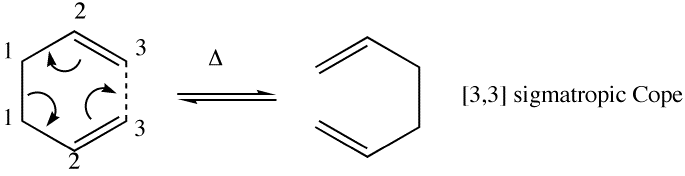
The Cope rearrangement is a [3,3] sigmatropic shift rearrangement of an allyl group migrating rather than a single carbon atom. It is accepted the reaction is thermally allowed via Huckel topology with suprafacial components and an electron count of 6(4n+2). This concerted reaction proceeds via a 'chair' or 'boat' transition state with the preferred reaction mechanism to be determined by finding the low-energy minima and transition structures on the C6H10 potential energy surface, from computational techniques.
Optimizing the Reactants and Products

First the reactant and product, 1,5-hexadiene is optimised at HF/3-21G level of theory, initially with an 'anti' linkage for the four central C atoms to give the anti1 conformer. This anti1 conformer gave a Hartree energy of -231.6926 a.u. and through selecting the symetrize function, obtained C2 symmetry for anti1.

1,5-hexadiene drawn in the 'gauche' linkage for the central four C atoms was optimised to give gauche4, with an energy of -231.69153 a.u., which is higher than the first anti1 conformer drawn. The gauche form being higher in energy is expected, as anti is generally more stable due to the allyl groups being less sterically hindered and hyperconjugation contribution. of . Also like anti1, the gauche4 confomer has C2 symmetry.
From the gauche4 structure the lowest energy conformation was deduced to be actually in a gauche form, which through altering the dihedral angle and bond angles to rotate the allyl group (C11-C7 in diagram) about the C7 atom, yielded the gauche3 conformer when optimised. Under this conformation gave the lowest energy of -231.69266 a.u. which indicates gauche3 is the most stabilised form of 1,5-hexadiene.

This can be explained by stabilisation contributed by lack of steric hinderence, hyperconjugation and also interaction of the allyl groups. The anti1 is more stable than the gauche4 because both are stabilised by hyperconjugation of the C-H σ bond with p-electron pair of double bond, but in anti1 the allyl groups are in a anti peri-planar like fashion which give least steric hinderence of the allyl groups and so is lower in energy. Gauche3 however is more stable than anti1 even though the anti displays significantly less steric hinderence of the allyl groups, because through investigation of the MOs of gauche3 reveals there is interaction between the two allyl group due to their orientation in gauche3, which anti1 nor guache4 does not contain. This allyl interaction must stablise the gauche3 as well as contribution of hyperconjugation and even though there is greater steric hinderence, all three contributions give gauche3 to be the lowest energy conformation.
 |
 |
 |

Next the Ci anti2 conformation was drawn and optimised first at HF/3-21G level of theory and then reopitmised at the B3LYP(6-31G*). Comparison of the two levels of theory shows there is little difference in the overall geometry of the conformer but the electronic energy on the bare potential energy surface is different. Using HF/3-21G method the energy is -231.69254 a.u. whereas the higher level B3LYP(6-31G*) method gives a lower energy of -234.55970 a.u.. A frequency analysis was performed on the optimised B3LYP/6-31G* structure to confirm the stationary point obtained is a minimum, by all the frequencies calculated being positive, i.e real.
Optimizing the 'Chair' and 'Boat' Transition Structures
The transition state structures of the cope rearrangement in 'chair' and 'boat' consists of two allyl fragments (CH2CHCH2) approximately 2.2Å apart. To set up a tranistion state optimisation first an allyl fragment was drawn and optimised at HF/3-21G level of theory, this was then copied onto the same window and oriented so that the two fragments look like the chair transition state. Optimisation of the chair transition state was performed first using the force constant method to optimise to a TS (berny) as shown in diagram. Frequency calculation gave an imaginary vibrational frequency at -817.86 cm -1 which corresponds to the cope rearrangement and confirms the transition state optimisation is correct.

The chair transition state was then optimised using the frozen coordinate method which in some cases produces a better transition structure by freezing the reaction coordinate through using Opt=ModRedundant and minimizing the rest of the molecule. Then once the molecule is fully relaxed, the reaction coordinate is unfrozen and the transition state optimization started again. First the Redundant Coord Editor was used to freeze the coordinate of the bond length of the terminal carbon atoms in the two allyl fragments. This was optimised as if it were a miniumum to give a structure similar to the chair transition I optimised using the force constant method but the bond breaking and bond forming distances are fixed to 2.2Å. The transition state opimisation is then set to optimise the bond forming/breaking distances but not through calculating the force constants like earlier, rather using a normal guess Hessian that is modified to include the two coordinates being differentiated along.
The transition structure obtained by the frozen coordinate method is very similar in geometry to the transition structure obtained by the force constant method, and the bond forming/breaking bond lengths are calculated to be the same for both structures at 2.02Å

| Energies | Hartree |
| Electronic | -231.619322 |
| Sum of electronic and zero-point | -231.466684 |
| Sum of electronic and thermal | -231.461322 |
Now the boat transition structure is optimised by using the QST2 method, where the reactants and products are stated for a reaction and the calculation will interpolate between the two structures to find the transition state between them. Here we had to make sure the reactants and products are numbered in the same way so I had to manually change the numbering by editing Atom List. The first QST2 optimisation was set up to find the job failed because it only translated the top allyl fragment and did not take into consideration possibility of rotation about the central bonds, to give a more dissociated chair transition like structure. Therefore the reactant and product geometries were modified to be closer to boat transition structure so it converges to the boat transition, as shown in diagram below.


| Energies | Hartree |
| Electronic | -231.602802 |
| Sum of electronic and zero-point | -231.450909 |
| Sum of electronic and thermal | -231.445287 |
The QST2 calculation was then performed again, this time converging to the boat transition structure. This was confirmed to be a transition state by there being only one imaginary frequency at -840 cm-1, with its vibrational motion synchronous with the σ bonds forming and breaking.

Next the Intrinsic Reaction Coordinate, IRC method was used to determine which conformer of 1,5-hexadiene is formed by following the minimum energy path from the transition structure down to its local minimum on a potential energy surface. This creates a series of points by taking small geometry steps in the direction where the gradient or slope of the energy surface is steepest. The IRC method was performed on the optimised chair transition structure only in the forward direction as the reaction coordinate is symmetrical and the number of points along the IRC was set to 50. However the structure did not reach a minimum geometry yet after the calculation as more points along the IRC were needed. Therefore I took the last point on the IRC and ran a normal minimization on the structure to yield the C2 gauche conformer with an energy of -231.691667 a.u.
| Energies | Chair TS | Boat TS |
| Electronic | -234.556983 | -234.543093 |
| Sum of electronic and zero-point | -234.414905 | -234.402326 |
| Sum of electronic and thermal | -234.408985 | -234.936001 |
The chair and boat transition structures were re-optimised using the B3LYP/6-31G* level of theory, starting from the HF/3-21G optimized structures and performing frequency analysis to confirm a transition state optimisation is obtained. Comparing the two levels of theory it can be seen there is little difference between the geometries of the transition structure but the relative energy difference between the reactants and transition states are quite different. Therefore it is better to optimise first at a lower level of theory to map the potential energy surface and then re-optimise at the higher level.
Activation energies via the chair and boat transition state is calculated at both 0 and 298.15K, by taking the difference between the (sum of the electronic and zero-point energies) of reactant anti1 and the chair/boat transition state, and multiplying it by 627.509 kcal/mol for Ea at 0K. For the activation energy at 298.15K the difference between the (sum of the electronic and thermal energies) of reactant anti1 and the chair/boat transition state is taken, and then multiplied by 627.509 kcal/mol.
Summary of activation energies (in kcal/mol)
| HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | Expt. | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | at 0 K | |
| ΔE (Chair) | 45.72 | 44.70 | 31.09 | 33.20 | 33.5 ± 0.5 |
| ΔE (Boat) | 55.61 | 54.78 | 41.97 | 41.33 | 44.7 ± 2.0 |
For the calculated activation energies, the boat transition structure always has higher activation energy than the chair transition structure. This is not surprising since for 6-membered rings the chair conformation is taken to be the most stable because there is minimal steric repulsion as the structure is staggered. The boat conformation however, is eclipsed which due to the torsional strain from eclising carbons and hydrogens results in an increase in energy.
Comparing with experimental values, its can be seen that activation energies calculated at B3LYP/6-31G* level of theory are markedly coherent, as the chair transition state calculations match very well the experimental values. For the boat transiton state there is a slight difference where the experimental activation energy is higher than that calculated.
The Diels Alder Cycloaddition
The famous Diels Alder reaction is a pericyclic reaction where the π orbitals of the dieneophile are used to form new bonds with the π orbitals of the diene, in either an allowed, concerted stereospecific fashion, or forbidden, not concerted. In terms of orbital interactions, the π/π* orbitals of the dieneophile interacts with the HOMO/LUMO of the diene to form two new bonding and anti-bonding MOs, in a [4s+2s] reaction. The nature of the transition state for the Diels Alder reaction is studied using computational techniques, both for a prototypical reaction and for the case where both diene and dieneophile carry substituents, and where secondary orbital effects are possible.
Cis-butadiene + Ethylene
 |
 |
For the Diels Alder reaction of ethylene and cis-butadiene, the ethylene approaches the cis form of butadiene from above. To form the transition structure, cis-butadiene was first optimised using the AM1 semi-empirical molecular orbital method, and the HOMO and LUMO plotted. The HOMO of cis-butadiene is observed to be anti-symmetric whereas the LUMO is symmetric. For ethylene, the π orbitals in the HOMO are symmetric and the π* orbitals in the LUMO are anti-symmetric.
The ethylene+cis butadiene transition structure has an envelope type structure, which maximizes the overlap between the ethylene π orbitals and the π system of butadiene. So a guess transition structure was made with interfragment distance set to 2.2Å and optimised using calculation of the force constant method to characterise the transition structure. The structure was confirmed to be a transition state by frequency analysis as there is only one imaginary frequency at -957cm-1. This vibration corresponds to the reaction path at the transition state and is synchronous with the formation of the two bonds, as shown on the jmol applet button. The lowest positive vibrational frequency however is a bending motion of the two fragments and is not synchronous with the formation of the two bonds. The transition structure is seen to have Cs symmetry with a σv plane in between the structure.

The partly formed σ C-C bonds have a bond distance of 2.12Å, whereas the typical sp3 C-C bond length is about 1.544Å, while a sp2 bond length is 1.338Å [1] and the Van de Waals radius of carbon is 1.70Å [2]. This shows that the partly formed σ C-C bonds are longer than the typical sp3 C-C bond length, but shorter than twice the Van der Waals radius of carbon. Therefore the C-C bond is in the process of forming, where it is not yet a full C-C bond.
The HOMO was plotted for the transition structure to reveal it is anti-symmetric with respect to the plane of symmetry. Therefore it can be seen that the anti-symmetric HOMO of cis-butadiene interacts with the anti-symmetric LUMO of ethylene and the symmetric LUMO of cis-butadiene interacts with the symmetric HOMO of ethylene, to form an anti-symmetric HOMO of the resulting adduct with two new σ bonds. This is labelled 'allowed' as the reaction proceeds in a concerted stereospecific fashion.
 |
 |
 |
1,3-Cyclohexadiene + maleic anhydride
To obtain the endo and exo transition state structures, the reactants 1,3-Cyclohexadiene and maleic anhydride where first optimised using the AM1 semi-empirical molecular orbital method. The optimised reactants were then used to create a guess transition structure with the interfragment distance set to 2.2Å which was optimised using the frozen coordinates method to characterise the transition structure.
| Endo TS | Exo TS | |
| Structure |  |

|
| Energy/ Hartree | -0.051505 | -0.050420 |
| Imaginary Frequency/ cm-1 | -806 | -812 |
| Vibration |
The calculated energy for the endo transition structure is lower than the exo transition structure which indicates that the endo transition state is more stable and the endo product is under kinetic control. The relative energies of the transition states can be explained in terms of steric and secondary orbital overlap effects.
For the exo transition state the C-C through space distance between the -(C=O)-O-(C=O)- fragment of maleic anhydride and 'opposite' -CH2CH2- group is 2.95Å, whereas for the endo transition state the C-C through space distance between the -(C=O)-O-(C=O)- fragment and 'opposite' -CH=CH- group is 2.89Å. There is steric repulsion between the fragment of maleic anhydride and the 'opposite' group so based on sterics the exo transition state is more stable because of the greater C-C through space distance and hence reduced steric hindrance.
Secondary orbital overlap is present in the transition state from the in phase interaction of the LUMO of -C=O in maleic anhydride and LUMO of -CH=CH-. This stabilisation is only present in the endo transition structure because the -(C=O)-O-(C=O)- fragment of maleic anhydride is 'opposite' the -CH=CH- group and the C-C through space distance is small, whereas for the exo the -(C=O)-O-(C=O)- fragment too far away to interact with the allyl group. Therefore mixing of LUMO orbitals decreases the energy of the transition state resulting in the endo transition structure being favoured despite the increase in steric repulsion.
 |
 |
The HOMO of the endo transition structure fails to show the secondary orbital overlap even though the interaction is present and stabilises the structure. This is due the low AM1 semi-empirical level of theory used which is not very accurate and if a higher level of theory was to be used the secondary orbital overlap interaction can be seen in the MOs.
Further Discussion
I decided to investigate an asymmetric Diels-Alder reaction of a 2-azadiene and an iminodienophile in the presence of a chiral Lewis acid which yields two diastereomers, exo and endo.[3] The exo confromer is taken to more stable and under thermodynamic control so through calculating the transition state structure by computational techniques the more stable conformer can be confirmed.
 |
 |
I chose to use AM1 semi-empirical molecular orbital method and first optimised the reactants 2-azadiene and iminodienophile as well as confirming the optimisation by frequency analysis. The optimised reactants were then used to create a guess transition structure with the interfragment distance set to 2.2Å which was attempted to be optimised using the frozen coordinates method to characterise the transition structure.
 |
 |
The transition state optimisation unfortunately failed to converge probably because the structure is too big and great steric hindrance of substituent groups. Therefore the trimethylsilicon carbonyl protecting group which is sterically very bucky was removed for the purpose of this exerise and replaced with smaller hydroxyl group. The transition state optimisation was attempted again but unfortunately failed again, probably still due to the same reasons as before. Therefore I was unable obtain the transition state structure and confirm exo is the most stable.
References
- ↑ M. J. S. Dewar and H. N. Schmeising, Tetrahedron, 1960, 11, DOI:10.1016/0040-4020(60)89012-6
- ↑ A. Bondi, J. Phys. Chem., 1964, 68, 441. DOI:10.1021/j100785a001
- ↑ E. Jnoff, L. Ghosez, J. Am. Chem. Soc., 1999, 121, 2617-2618.
