Rep:Mod:LOTR2
Structural Analysis of BCl3
| Frequency/cm-1 | IR Intensity |
| 214 | 4 |
| 214 | 4 |
| 380 | 44 |
| 414 | 0 |
| 932 | 259 |
| 932 | 259 |
The D3h ground state structure of BCl3 was optimised with the geometry shown below, and is confirmed to be a minima by frequency analysis, as the frequencies of all six vibrations of BCL3 are positive.

The calculation method used to optimise the D3h ground state structure of BCl3 is B3LYP and the basis set is 3-21G. The same basis set and method must be used for both calculations so the same type of approximations are made in solving the Schrodinger equation with same level of accuracy in order to use vibrational anaysis to confirm BCl3 optimised is minima.
Frequency analysis determines whether first derivative of the potential energy surface at zero, i.e. a stantionary point, is a maximum (transition state) or minimum (ground state). This is achieved from finding the second derivative which is the curvature of the function, where if the second derivative is postive the stationary is a minimum and vice-versa. The frequencies calculated are essentially the second derivative of the potential energy surface so if the frequencies are all positive then it is a minimum, the ground state structure.
| Calculated | Literature | |
|---|---|---|
| B-Cl bond length/Â | 1.87 | 1.72 |
| Cl-B-Cl bond angle/° | 120.0 | 120.0 |
The calculated Cl-B-Cl bond angle accurately corresponds with literature[1] however the B-Cl bond distance is slightly greater than the reported experimental value and is not very accurate due to using a low level basis set to optimise BH3 which gives low accuracy and fast calculations as a result.
Gaussview in some structures does not draw the bonds between atoms where it is expected because it only draws bonds based on a distance criteria, so the lack of a bond means the distance is greater than some pre-defined value. Therefore a bond is the electrostatic interaction of two atoms to form molecular orbitals from their atomic orbitals.
Vibrational and MO Analysis of BH3

The IR spectrum of BH3 displays only 3 peaks when there are actually six vibrations because the vibrations at 1204 and 2737 cm-1 are degenerate with a symmetry of E', therefore the peaks of degenerate vibrations overlap giving a single peak. Also the vibration at 2598 cm-1 has zero IR intensity so no peak is displayed on th spectrum.

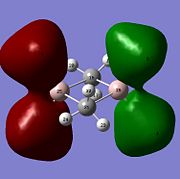
Molecular orbitals of BH3 were calculated by performing a population analysis (https://www.ch.imperial.ac.uk/wiki/index.php/Image:RITEN_BH3_POP.LOG). These computed MOs can be compared with the approximate MOs produced from the MO diagram of trigonal planar D3h BH3 by linear combination of atomic orbitals (LCAO). As the unoccupied orbitals are more diffuse, the occupied and LUMO orbitals are compared to reveal the 'LCAO' MOs are very similar to the 'real' MOs, except for the major difference that the 'real' MOs spread over the molecule with same sign wavefunctions of the atomic orbitals mixing to give larger electron wavefunctions of the molecular orbitals. The 2a'1 orbital is totally symmetric with greater contribution from the fragment MO H3 as it is closer in energy, the HOMO is degenerate with e' symmetry while the LUMO is non-bonding pz orbital with a"2 symmetry and is low in energy due to non-bonding and Boron being electropositive. As the qualitative MO theory is very accurate with the quantitative 'real' MOs, the LCAO approach is very useful for predicting the molecular orbitals of molecules and determining the HOMO and LUMO which can tell the chemical nature of the molecule.
From natural bond order analysis electron density of the whole molecule is partitioned out into hybrid orbitals with varying contributions from atomic orbitals. For B-H bond, σBH= 0.6830(sp2.00)B + 0.7304(sp2.00)H, where 46.65% of the bond is contributed by B orbitals of hybridisation 33%s+66%p, and 53.35% is from H orbital of 100%s. Therefore Boron forms 3 sp2 orbitals which each interact with sAO of Hydrogen.
Cis and Trans Isomerism of TM complex
The cis and trans ground state isomers of Mo(CO)4(PCl3)2 were initially optimised using B3LYP method and the low level basis set LANL2MB to get the rough geometry and then through altering the torsion angle of the PCl3 groups the new geometry was optimised using the B3LYP method but with a better basis set and pseudo-potential, LANL2DZ.
 |
 |
The optimisations were confirmed to be minima by frequency analysis, where for the cis isomer (freq analysis: http://hdl.handle.net/10042/to-3838) all 45 vibrational frequencies are positive with the lowest frequency at 11 cm -1. For the trans isomer (freq analysis: http://hdl.handle.net/10042/to-3839) all expect one vibrational frequencies are positive, where the lowest frequency is -2 cm -1, however this is due to numerical difficulties and can still be considered all positive and hence a minimum.
| Cis- optimised | Cis- Lit. | |
|---|---|---|
| Mo-P | 2.51 | 2.56 |
| Mo-C (trans to P) | 2.01 | 1.99 |
| Mo-C (trans to C) | 2.06 | 2.03 |
| P-Mo-P | 94.2 | 107.3 |
| P-Mo-C (trans) | 176.1 | 166.8 |
| C-Mo-C (trans) | 178.3 | 174.3 |
| Trans- optimised | Trans- Lit. | |
|---|---|---|
| Mo-P | 2.45 | 2.50 |
| Mo-C | 2.06 | 2.01 |
| P-Mo-P | 180.0 | 180.0 |
| P-Mo-C(1) | 91.3 | 92.0 |
| P-Mo-C(2) | 90.0 | 87.2 |
The optimised geometries of the cis and trans isomer can be compared with experimental literature values to give an estimate of a rough range for bond length and bond angle. Geometric parameters of the optimised cis isomer is compared with literature values of cis-tetracarbonylbis[tris(p-fluorophenyl)-phosphine]Molybdenum (cis-[Mo(CO)4(C18H12F3P)2]) [2] as shown in the table, and show the relevant bond lengths are quite accurate with experimental values within 0.1Å. The relevant bond angles however are not so accurate and indicates the optimisation at this basis set quite good but a higher level basis set would give more accurate results.
The optimised trans isomer is compared with literature geometric parameters of trans- [Mo(CO)4(PPh3)2][3] as shown in the table, and compare very well within 0.1Å for the relevant bond lengths and within 2° for the bond angles. This confirms a decent level of accuracy at this basis set for the optimised geometry.
| cis- calculated | cis- Lit. | symmetry |
|---|---|---|
| 1945.3 | 1886.7 | B2 |
| 1948.7 | 1898.5 | B1 |
| 1958.4 | 1913.7 | A1 |
| 2023.3 | 2012.4 | A1 |
| trans- calculated | trans- Lit. | symmetry |
|---|---|---|
| 1950.9 | 1885.4 | Eu |
| 1977.1 | n/a | B1g |
| 2031.0 | n/a | A1g |
The relative energies of the cis and trans isomers are -623.577 a.u and -623.576 a.u repectively, and as the cis isomer is lower in relative energy this is the thermodynamically more stable stereoisomer. The energy difference between the two isomers is calculated to be 0.00115 a.u or 3 kJ/mol, which is a very small energy difference indicating that at higher temperatures the isomer can easily interchange into one another due to the low difference in energy between them. In order to alter the relative ordering of the cis and trans isomer the PR3 ligand can be made more sterically hindered by the introduciton of bulky R substituents such as i-Pr. Greater steric hinderence of PR3 would induce the trans isomer to be more stable as the bulky substituents would want to be furthest apart only possible in a trans-conformation.
The vibrational frequencies of the isomers which have low value frequencies (-2cm -1 for trans- and 11 cm -1 for cis-) is due to the PCl3 group rotation about the P atom. At room temperatures this rotation is very facile giving rise to very low frequency values, even slightly negative values.
Computed IR carbonyl frequencies do not corrrectly compare with experimental values because the vibrational frequencies are computed in the gas phase whereas experimental IR spectroscopy is performed in the solution phase, which leads to differing frequencies of the vibrational modes.
Not all vibrational modes of carbonyl are shown the IR spectrum because the frequencies have zero intensity due to the no change in dipole moment of the molecule from symmetric vibrational modes, as the dipole moments cancel out and give zero intensity.
 |
 |
Mini Project
I have chosen to investigate the structures of R3Al which dimerise through the formation of Al-R-Al 2e3c bridging bonds. I have taken the R group to be a methyl group and also a hydrogen atom, to determine if the trimethyl Aluminium (and Aluminium hydride) dimer is more stable than the monomer and rationalise this stability. I will also investigate the Boron analogue, i.e diborane and trimethyl Boron dimer, and compare these results accordingly. I will examine the electronic structure of the dimer through MO and NBO anaylsis and finally compare if trimethyl Aluminium and trimethyl Boron can thermodynamically form a dimer analogue with B-Me-Al bridging bonds.
The calculation method used to optimise the monomer and dimer structures is the RB3LYP with a decent basis set of 6-311G(d,p). All calculations were run with this basis set and method so results can be compared and every optimisation was confirmed to be a minima by frequency analysis.
Me3Al dimerisation
| 2 x |  |
———————————> |  |
 |
 |
Vibrational analysis of trimethyl Aluminium (http://hdl.handle.net/10042/to-3932) and its dimer (http://hdl.handle.net/10042/to-3933) confirmed both optimisations to be minima with all vibrational frequencies for Me3Al and Me6Al2 positive, as shown in the IR spectra.
| Me3Al | Me6Al2 | Me6Al2 Lit | |
|---|---|---|---|
| Energy | -362.25 | -724.52 | n/a |
| Al-Ct | 1.97 | 1.97 | 1.93 |
| Al-Cb | n/a | 2.16 | 2.15 |
| Al--Al | n/a | 2.64 | 2.70 |
| Ct-Al-Ct | n/a | 122.6 | 125.8 |
| Cb-Al-Cb | n/a | 104.8 | 102.0 |
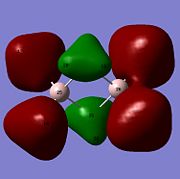
Comparing geometric parameters of the dimer with literature[4] shows calculated bond lengths within 0.1Å and bond angles within 3°, confirming an accurate enough match with experimental values at this basis level and that the calculations made are correct. The calculated bond distance of Al with the terminal carbon (Al-Ct) of 1.97Å is exactly the same as the calculated normal Al-C bond length in trimethyl Aluminium, whereas Al with the terminal carbon(Al-Cb) bond length is longer by 0.19Å. This longer bridging Al-C bond distance signifies a reduced bond order due to formation of 2e3c bonds. Also the bridging methyl groups adopt a staggered conformation with respect to each other to give the dimer C2h symmetry rather than the eclipsed bridging methyl groups and Cs symmetry.
Relative energies of the monomer and dimer can be used to calculate the energy difference and deduce which one is more thermodynamically stable.
ΔE = E(Me6Al2) - 2xE(Me3Al) = -0.013 a.u = -34 kJ/mol
The difference in energy of the monomer and dimer is negative, indicating the product dimer is thermodynamically more stable by an energy of 34 kJ/mol.
From NBO analysis (http://hdl.handle.net/10042/to-3962) the bonding present between the bridging methyl group and Al atom is given to be:
For the C16−Al26 bond(see picture for atom label), the hybrid composition is 0.9312(sp1.92)C16 + 0.3623(sp5.08)Al26; where 86.87% of the bond is contributed by C16 orbitals of hybridisation 34.22%s+65.76%p, and 13.13% is from Al26 orbital of hybridisation 16.22%s+82.38%p; with an occupancy of 1.747e.
For C21−Al26 bond, the hybrid composition is 0.9317(sp1.91)C21 + 0.3632(sp5.03)Al26; where 86.81% of the bond is contributed by C21 orbitals of hybridisation 34.38%s+65.61%p, and 13.19% is from Al26 orbital of hybridisation 16.36%s+82.22%p; with an occupancy of 1.750e.
Therefore there are two bond-like interactions between both bridging C16 and C21 with Al26 and none with the other Al atom, Al25.
 |
 |
 |
 |
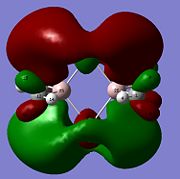 |
From the 'Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis' section the calculations reveal several donations of σ-bonded electrons to unfilled nonbonded n* orbitals of Al25.
σ(C16-H20) donates to n*Al25 with stabilisation energy of 20.95 kcal/mol. σ(C16-Al26) donates to n*Al25 with stabilisation energy of 92.68 kcal/mol. σ(C16-Al26) donates to n*Al25 with stabilisation energy of 27.63 kcal/mol. σ(C21-Al26) donates to n*Al25 with stabilisation energy of 91.31 kcal/mol. σ(C21-Al26) donates to n*Al25 with stabilisation energy of 27.86 kcal/mol.
Therefore NBO analysis has assigned two σ interactions for C16-Al26 and C21-Al26, and then donation of the electrons in these interaction 'bonds' to n*Al25 to make a 'bond' for C16-Al25 and C21-Al25, with high stabilisation energy of about 91 kcal/mol. This represented is not correct as the two electrons are actually spread over all three atoms (C and two Al), hence 2e3c bonds which NBO fails to recognise because of its lewis acidity approach.
H3Al dimerisation
| 2 x |  |
———————————> |  |
 |
 |
Vibrational analysis of Aluminium hydride (http://hdl.handle.net/10042/to-3965) and its dimer (http://hdl.handle.net/10042/to-3966) confirmed both optimisations to be minima with all vibrational frequencies for H3Al and H6Al2 positive, as shown in the IR spectra.
| H3Al | H6Al2 | |
|---|---|---|
| Energy | -244.23 | -488.51 |
| Al-Ct | 1.58 | 1.57 |
| Al-Cb | n/a | 1.74 |
| Al--Al | n/a | 2.62 |
| Ct-Al-Ct | n/a | 82.4 |
| Cb-Al-Cb | n/a | 128.0 |
ΔE = E(H6Al2) - 2xE(H3Al) = -0.051 a.u = -134 kJ/mol
The difference in energy of the monomer and dimer is very negative, indicating the product dimer is thermodynamically much more stable by an energy of 134 kJ/mol.
H3B dimerisation
| 2 x |  |
———————————> |  |
 |
 |
Vibrational analysis of borane (http://hdl.handle.net/10042/to-3970) and its dimer diborane (http://hdl.handle.net/10042/to-3969) confirmed both optimisations to be minima with all vibrational frequencies for borane and diborane positive, as shown in the IR spectra.
| H3B | H6B2 | H6B2 Lit | |
|---|---|---|---|
| Energy | -26.62 | -53.30 | n/a |
| B-Ct | 1.19 | 1.19 | 1.19 |
| B-Cb | n/a | 1.32 | 1.33 |
| B--B | n/a | 1.76 | 1.77 |
| Cb-Al-Cb | n/a | 95.8 | 97 |
Comparing geometric parameters of the dimer with literature[5] shows calculated bond lengths within 0.01Å and bond angles within 2°, confirming an accurate match with experimental values at this basis level and that the calculations made are correct.
ΔE = E(H6B2) - 2xE(H3B) = -0.062 a.u = -163 kJ/mol
The difference in energy of the monomer and dimer is very negative, indicating the product dimer is thermodynamically much more stable by an energy of 163 kJ/mol.
Me3B dimerisation
| 2 x |  |
———————————> |  |
 |
 |
Vibrational analysis of trimethyl Boron (http://hdl.handle.net/10042/to-3974) and its dimer (http://hdl.handle.net/10042/to-3975) confirmed both optimisations to be minima with all vibrational frequencies for Me3B and Me6B2 positive, as shown in the IR spectra.
| Me3B | Me6B2 | |
|---|---|---|
| Energy | -144.656 | -289.263 |
| B-Ct | 1.58 | 1.61 |
| B-Cb | n/a | 1.82 |
| B--B | n/a | 1.90 |
| Ct-B-Ct | n/a | 114.9 |
| Cb-B-Cb | n/a | 115.3 |
Initial optimisation of Me6B2 gave bridging methyl groups in eclipsed conformation with Cs symmetry and relative energy of -289.264 a.u, which proved to be a minima by frequency analysis; however through manually rotating the methyl groups in a staggered conformation and opitmising again, yielded a higher relative energy of -289.263. This indicates the eclipsed conformation of the bridging methyl groups the more stable with an small energy difference of 2.8 kJ/mol
ΔE = E(Me6B2) - 2xE(Me3B) = -0.049 a.u = -129 kJ/mol
The difference in energy of the monomer and dimer is very negative, indicating the product dimer is thermodynamically much more stable by an energy of 129 kJ/mol.
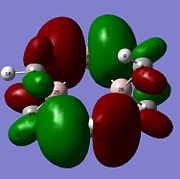
From NBO analysis (https://www.ch.imperial.ac.uk/wiki/index.php/Image:ME6B2_POP.LOG) the bonding interaction present between the bridging methyl group and B atom is given to be:
For the B1-C18 bond(see picture for atom label), the hybrid composition is 0.5216(sp4.10)B1 + 0.8532(sp2.02)C18; where 27.20% of the bond is contributed by B1 orbitals of hybridisation 19.59%s+80.24%p, and 72.80% is from C18 orbital of hybridisation 33.07%s+66.90%p; with an occupancy of 1.599e.
For B1-C23 bond, the hybrid composition is 0.5215(sp4.10)B1 + 0.8532(sp2.02)C23; where 27.20% of the bond is contributed by B1 orbitals of hybridisation 19.58%s+80.24%p, and 72.80% is from C23 orbital of hybridisation 33.07%s+66.89%p; with an occupancy of 1.599e.
Therefore there is a bond-like interaction between bridging C-18 and C-23 with B-1 and none with the other Al atom, B-2.
From the 'Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis' section the calculations also show donations of σ-bonded electrons to unfilled nonbonded n* orbitals of B-2, just as for trimethyl aluminium dimer.
σ(B1-C18) donates to n*B2 with stabilisation energy of 211.92 kcal/mol. σ(B1-C18) donates to n*B2 with stabilisation energy of 68.63 kcal/mol. σ(B1-C23) donates to n*B2 with stabilisation energy of 212.09 kcal/mol. σ(B1-C23) donates to n*B2 with stabilisation energy of 68.59 kcal/mol.
This shows the two assigned σ interactions for C16-Al26 and C21-Al26 donate the electrons in these interaction 'bonds' to n*Al25 to make a 'bond' for C16-Al25 and C21-Al25, with very high stabilisation energy of about 212 kcal/mol.
 |
 |
Me3B + Me3Al dimerisation analogue
 |
+ |  |
———————————> |  |
 |
Vibrational analysis of Me6BAl (http://hdl.handle.net/10042/to-4069)(Me3Al and Me3B have already been done) confirmed the optimisation to be minima with all 72 vibrational frequencies positive as shown in the IR spectra.
| Me6BAl | |
|---|---|
| Energy | -506.895 |
| Al-Ct | 1.96 |
| B-Ct | 1.62 |
| Al-Cb | 2.13 |
| B-Cb | 1.78 |
| B--Al | 2.29 |
| Ct-Al-Ct | 120.9 |
| Ct-B-Ct | 114.4 |
| Cb-Al-Cb | 92.5 |
| Cb-B-Cb | 119.9 |
ΔE = E(Me6BAl) - (E(Me3B)+E(Me3Al)) = 0.014 a.u = 37 kJ/mol
The energy difference of products minus reactants, gives a positive value and so indicates the trimethyl boron and aluminium monomers is more themodynamically stable than the formation of the dimer analogue.
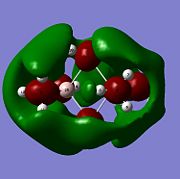
Comparing the relative bond lengths of the bridging methyl groups with the boron and aluminium centre, shows the B-Cb bond distance is shorter than Al-Cb indicating the methyl groups are closer to the boron atom and further apart from Aluminium. A shorter bond lenth deduces stronger bond formation for B-Cb and is likely to be the σ bond that gets formed and donates to the n*Al. This can be confirmed be NBO analysis;
For the B1-C17 bond, the hybrid composition is 0.5388(sp3.85)B1 + 0.8424(sp1.76)C17; where 29.03% of the bond is contributed by B1 orbitals of hybridisation 20.58%s+79.28%p, and 70.97% is from C17 orbital of hybridisation 36.17%s+63.08%p; with an occupancy of 1.855e.
For B1-C22 bond, the hybrid composition is 0.5411(sp3.73)B1 + 0.8409(sp1.72)C22; where 29.28% of the bond is contributed by B1 orbitals of hybridisation 21.13%s+78.74%p, and 70.72% is from C22 orbital of hybridisation 36.73%s+63.24%p; with an occupancy of 1.862e.
σ(B1-C17) donates to n*Al26 with stabilisation energy of 66.60 kcal/mol. σ(B1-C22) donates to n*Al26 with stabilisation energy of 58.50 kcal/mol. σ(C17-H18) donates to n*Al26 with stabilisation energy of 25.09 kcal/mol.
Therefore it can be seen through NBO analysis that σ interactions of B1-C17, B1-C22 and C17-H18 donate electrons in these interaction 'bonds' to the n*Al26 to make a 'bond' for C17-Al26 and C22-Al26.
References
- ↑ S. Reinhardt, M. Gastreicha and C. M. Marian, Phys. Chem. Chem. Phys., 2000, 2, 955-963.
- ↑ E. C. Aly, G. Ferguson, J. F. Gallagh and S. Song, Acta Cryst., 1994, C50, 1084-1087.
- ↑ G. Hogarth, T. Norman, Inorganica Chiraica Acta, 1997, 254, 167-171.
- ↑ G. S. McGrady, J. F. C. Turner, R. M. Ibberson and M. Prager, Organometallics, 2000, 19, 4398-4401
- ↑ CRC Handbook of Chemistry and Physics






