Rep:Mod:LMV276

The Free Energy and Thermal Expansion of MgO

Abstract

Two different methods of simulations were used to predict behaviour of MgO crystal structure, specifically its thermal expansion. Thermal expansion coefficient $\alpha$ was determined. The first method, Quasi-Harmonic Approximation gave result as change in volume based on differences in free energy with change in temperature, molecular dynamics method allowed to simulate actual vibrational motions in the structure giving average over time result. The values of $\alpha$ were determined as 2.678 x 10^-5 K^-1 and 3.01117x 10^-5 K^-1 respectively. Limits and advantages of both methods were compared.

Introduction

Figure 1: MgO, primitive cell

Crystal structure can be described as a repeating pattern of atoms over a large range. The basic unit in a crystal is a primitive cell which by translation builds up into the hypothetically infinite structure. An example of a crystal structure is MgO which can be described by face centered unit cell with a cell parameter a. For a conventional cell, a is equal to the side of the cube. The periodicity of a crystal defines its physical properties. A crystal structure can be described either in real space or in reciprocal space, also called k-space with lattice parameter a* which can expressed as $a*=\frac{2\pi }{a}$.

The primitive cell in k-space is called Brillouin zone and spins between values $\frac{-\pi }{a}$ and $\frac{\pi }{a}$. Within this space every vibrational state corresponds to a unique k value. The periodical identity of lattice is retained in k-space.

MgO can be described by different types of cells; conventional cell consisting of 4 MgO units is mainly used to visualize the structure but is not suitable for calculations done in this experiment. Instead primitive cell of a rhombohedron shape and supercell, a representation of a larger system, were used.

Figure 2: MgO, 2x2x2 supercell with 32 Mg0 units

Atoms in a crystal structure experience lattice vibrations. The vibrations are not independent but collective. In reference to photons, these collective vibrations are called phonons. The phonons hold the energy of the lattice. Graphing vibration frequencies over Brillouin zone gives dispersion curve and rise to branches. Lower branches are called acoustic which converge to minimum at origin, higher branches are optical. A structure with N atoms gives rise to 3N branches as each atom has related 3 degrees of freedom. Summation over possible states related to a k point at a specific k gives density of states (DOS).

Temperature influences properties of the structure of a crystal. With increasing temperature, there is a change in the cell parameter, therefore also volume, internal and free energy, vibration movement is more vigorous. The extent of thermal expansion can be described by thermal expansion coefficient $\alpha$ which gives a value by which the lattice expands over a step in temperature. Thermal expansion coefficient can be determined from change in volume with temperature at constant pressure.

$\alpha =\frac{1}{V_0}{\left(\frac{\partial V}{\partial T}\right)}_P$ where V₀ is equal to the initial volume.

Aproximations

Interactions between atoms in the crystal were set to purely ionic. The attraction is equal to Coulombic forces. Short repulsive wall set as Buckingham potential was applied to prevent collapse of the ionic structure.

---

Methodology

Lattice Dynamics and Quasi-harmonic approximation

This method is based on harmonic approximation which arises from performing Taylor expansion on energy between neighbouring unfixed atoms in a chain. Lattice energy is described only by first two terms, others are neglected, giving the lattice energy the parabola shape of a harmonic oscillator. The approximation gives accurate results at low temperature but it does not consider thermal effects. Therefore, the approximation is expended to quasi-harmonic (QHA) which incorporates phonon frequency dependce on volume and structure via Helmholtz free energy, A.

$A=E_0+\frac{1}{2}\sum _{\mathbf{k},i}\hslash {\omega }_j{,}_k+k_{B}T\sum _{\mathbf{k},i}ln[1-exp(\frac{-\hslash {\omega }_j{,}_k}{k_{B}T})]$ where E₀ is the lattice energy, j represents phonon bands, ω angular frequency

The second term in the equation stands for zero point energy, energy at 0K, third term is the vibrational entropy.

Helmholtz free energy can be also expressed as $dA=dU-TdS-SdT=-pdV-SdT$ In the simulation, temperature is fixed, vibrational entropy is calculated and free energy is estimated. Helmholtz free energy varies with temperature and volume, as temperature is fixed, from the calculated free energy, change is volume is determined. QHA breaks at higher temperatures as it does not allow bonds to be broken. The calculations are done on primitive cell.

Molecular Dynamics

Compared to quasi-harmonic approximation, molecular dynamics is strictly classical method. The simulation is carried out in real space on MgO 2x2x2 supercell containing 64 atoms to give enough space for the free movement of the atoms. The base of the molecular dynamic simulation is Newton's law of motion, where $F=ma$. With every step, accelaration is computed and and a new position of an atom is determined. The behaviour of the system is followed over time until the system is minimized. With change in temperature kinetic energy of the system changes and so does the volume of the system. As this method is classical, it does not give access to values of zero point energy. However, compared to quasi-harmonic approximation, it allows the atoms to move and the bonds to be broken therefore it is suitable for simulations at higher temperatures. The time-step was set to 10^-15, the equilibration was done on 500 steps, sampling and trajectory write were set to 5 steps. This set up, including the size of the supercell is a compromise between accuracy of results and time demand of the calculations. Programs used in this experiment were DLVisualize for visualization and GULP (General Utility Lattice Program) for running the simulations.

---

Results and Discussion

Lattice dynamics

Figure 3: phonon dispersion

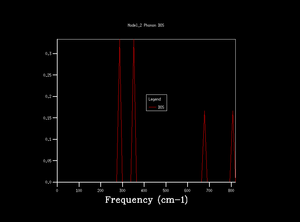
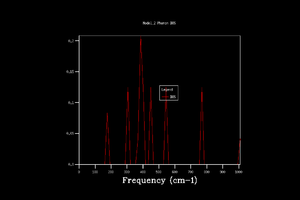
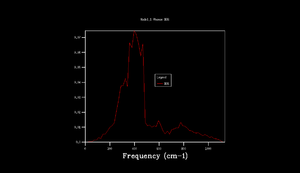
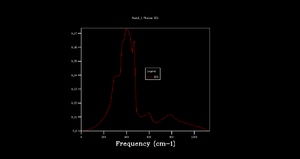
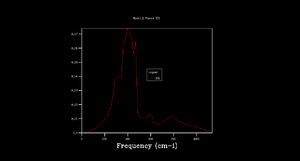
Phonon dispersion was computed for MgO primitive cell over 50 k points spinning between ±$\frac{\pi }{a}$ (Figure 1). High symmetry points W, L, Γ, X, K were labeled. 0 k point is labeled as Γ. Acoustic branches reach minimum value at Γ. There are 6 branches, 3 acoustic, 3 optical which is a result expected for 2 atoms in 3D. At some k points the branches converge. Density of states (DOS) was calculated for grid 1x1x1 (Figure 2).The calculation was done on one k point chosen by the program, particularly L point (0.5,0.5,0.5). DOS shows 4 peaks. 6 peaks were expected but looking at phonon dispersion graph (Figure 1) at this point, 2 pairs of vibrations converge therefore two peaks at lower frequencies are doubly degenerate which also relates to their relative intensities: peaks at 286 and 351 Hz are twice the height of the other peaks at 676 and 806 Hz.

Figure 4: DOS curves with varied shrinking factors applied

Phonon DOS of a 1x1x1 grid	Phonon DOS of a 2x2x2 grid	Phonon DOS of a 4x4x4 grid
Phonon DOS of a 8x8x8 grid	Phonon DOS of a 16x16x16 grid
Phonon DOS of a 32x32x32 grid	Phonon DOS of a 64x64x64 grid

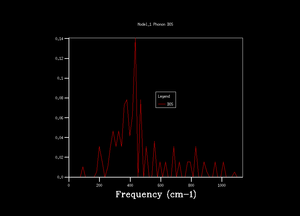
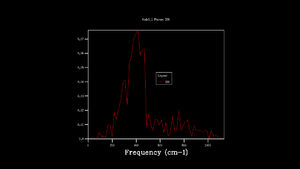
To obtatin more representable DOS, the grid was changed. By changing the grid, shrinking factor, IS, was introduced into the computation. Shrinking factor is related to idea of folding the phonon dispersion curve and therefore increasing number of k points and obtaining more vibration modes. As the grid size was being increased more peaks emerged, slowly giving a smoother graphical representation of DOS. When looked at DOS calculated with grid size 32x32x32 and 64x64x64, there was no visible difference. For that reason, it was decided to use 32x32x32 grid for further simulations as it gives optimal balance of accuracy and speed (14 s CPU time compared to 820 s for 64x64x64 grid). This choice was also proved by comparing calculated Helmholtz free energy, A, for each grid. The difference in A was larger for DOS calculation with low grid size, at IS 32 the free energy converged, establishing Helmholtz free energy to -40,926483 eV at 300 K and proving that computations with 32 grid size gives reasonable data for this experiment. Lower grid size than 32 gave less smooth density of state graph and the Helmholtz free energy values did not converge. The lower grid size did not contain enough vibrations to give accurate results. The program also calculates heat capacity which converges at lower grid size compared to free energy.

Figure 5: Helmhotz free energy for different grid size

Grid size	A (eV)	ΔA (eV)
1x1x1	$-40.930301$
2x2x2	$-40.926609$	0.356196
4x4x4	$-40.926450$	0.015391
8x8x8	$-40.926478$	0.002704
16x16x16	$-40.926482$	0.000457
32x32x32	$-40.926483$	6.1 x 10-5
64x64x64	$-40,926483$	7 x 10-6

In case the accuracy of the calculations of energy was needed to be accurate to 1 meV per cell,8x8x8 grid size could be used instead. If the accuracy was required up to 0.5 meV or 0.1 meV, 16x16x16 grid size would be sufficient.

It was considered whether 32x32x32 would be accurate grid size also for experiments with other crystal structures, specifically with similar oxide, zeolite and a metal. MgO and CaO have the same structure and their lattice parameters, a are quite similar. For conventional cell at room temperature, a of MgO equals to 4.212 Å compared to 4.808 Å for CaO . Therefore, for the same experiment with CaO, the same grid size (32x32x32) would be used. Faujisite, a representing of zeolite has roughly 5 times larger lattice parameter, (a = 24.6-25 Å) . That means that in reciprocal space a* is smaller than for MgO, therefore lower grid size would obtain the same accuracy. When comparing MgO to a metal, it is first looked upon their dispersion curves. The sea of electron in metals has a shielding effect due to the repulsive interactions resulting in low dispersion in metals. As the branches for a metal are flat, less sampling is needed, therefore for metals smaller grid size can be used as well to obtain reasonable data.

Figure 6: Helmholtz free energy temperature dependence

A series of DOS computations was run on a range of temperature using the grid size 32x32x32. From the results, change in free energy A, lattice parameter a, and volume V was observed. Free energy increased in absolute value with increasing temperature (Figure 3). Such behaviour was expected from the expression for A, as temperature is increased the entropy term becomes more dominant and also entropy values increases as more energy levels become available. Lattice parameter and volume also increased. (Figure 4,5). When looked closely at the graph of change in volume depending on temperature, there is noticeable linear trend between temperatures 300-1000K. At lower temperatures the trend line flattens, the values being ruled by zero point energy, change in entropy term and expansion is minimal. The crystal behaves at lower temperatures according to harmonic approximation . At high temperatures the results were inaccurate as the bonds were not allowed to break and at 3000 K the simulation broke. This temperature was critical as it is in the range of melting point of MgO (3098 K)

Figure 7: Change in lattice parameter a with change in temperature

Figure 8: Change in lattice parameter a with change in temperature, QAH method

From the linear part of the graph slope was determined: $\frac{\mathrm{\Delta }V}{\mathrm{\Delta }T}=0.0005$. To obtain thermal expansion coefficient $\alpha$, this value was divided by initial volume V₀ = 18.6804 ų. Resulting $\alpha$ equals to 2.678 x 10^-5 K^-1.

Molecular dynamics

Figure 9: Change in lattice parameter a with change in temperature, MD method

For this method 2x2x2 supercell was used to be able to run the simulation on collective movement of the atoms. Using supercell compared to the previous part of the experiment correlates with using shrinking factor. To run the simulation with the same number of vibration modes, supercell of size 32x32x32 would have to be used. However, that would be very time demanding therefore 32 unit MgO was defined instead. The system fluctuates but as the data was averaged over large number, the limitation is minimal, only at high temperatures (above 2000 K) the fluctuation was noticeable. The simulation was run on NPT ensemble, again following the change in volume over temperature range. (Figure 6) This time free energy was not examined as the simulation calculates internal energy but not free energy. The volume was increasing linearly across the set range 100-1000 K. At higher temperatures around melting point the simulation still worked though there was a change in trend. Thermal expansion coefficient $\alpha$ was calculated from the slope as before in the first method obtaining the value 3.01117x 10^-5 K^-1.

Comparison of the results

Figure 10: Comparison of the Volume changes for both methods

In literature, $\alpha$ 1.39 x 10^-5 K^-1 was obtained via x-ray diffraction over the range 25 K to 1000 K. . This value is lower than both values obtained in this experiment 2.678 x 10^-5 K^-1 for QHA and 3.01117x 10^-5 K^-1 for MD. The differences arise from the approximations used in this experiment, firstly simulating a perfect defect-less crystal structure, secondly considering the interaction to be purely ionic without any covalent interaction and defining the interactions.

The difference between the simulation methods is a result of the limits of both methods and approximation of their energies. The main difference is at behaviour at high temperatures where QHA fails whereas MD method goes over the critical temperature but no longer being linear. MD compared to QHA considers anharmonic vibrations but on the other hand, MD method does not consider zero point energy so the calculations cannot be done at 0 K as there is no kinetic energy. MD is limited by the time demand and the size of supercell used which lowers the accuracy of the method.

---

Conclusion

In this experiment, two simulation methods were compared by studying thermal expansion of MgO crystal structure. Value of thermal expansion coefficient was larger for both methods compared to literature due to the approximations made. Quasi-harmonic approximation fails at high temperature but gives accurate results quickly at low temperature and includes zero point energy. Molecular dynamics is preferred method for simulating at higher temperatures but its accuracy is limited by its time demands and therefore use of a small supercell then desired. As a possible extension of this experiment, other thermodynamic properties could be studied, for example heat capacity.

---