Rep:Mod:LMB456

The Cope Rearrangement

This [3,3]-sigmatropic shift rearrangement has been the subject of many experimental and computational studies. For a long time it was debated as to whether it’s controversial mechanism was concerted, stepwise or dissociative. Nowadays it is generally accepted that the reaction occurs in a concerted fashion via either a "chair" or a "boat" transition structure, with the "boat" transition structure lying several kcal/mol higher in energy.

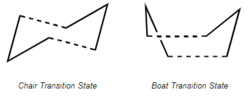
The B3LYP/6-31G* level of theory has been shown to give activation energies and enthalpies in remarkably good agreement with experiment. This is demonstrated using Gaussian calculations.

HF/3-21G of Anti and Gauche conformers of 1,5-hexadiene

The following conform was used as a first run in Gaussian: Anti-conformation 2 of 1,5-hexadiene

The structure was optimized at the HF/3-21G level of theory. The method used in the Gaussian Optimization was Hartree Fock and the default basis set used was 3-21G. The energy calculated was -231.69253528 au. This value represents the energy of the molecule on the bare potential energy surface. After using the symmetrize function it was found that the point group of the molecule was said to be C_i. This was identified as the anti-conformation 2 from the appendix given.

From inspection of the different conforms of 1,5-hexadiene it is expected that this conformation is the lowest conformation and thus activation energies and enthalpies would be calculated from this structure.

For comparison a gauche conformer was inspected. This was the conform: Gauche-conformation 3 of 1,5-hexadiene

It was expected that the energy be of higher energy than the anti-periplanar arangement due to the steric clashes faced in the gauche conformation. The structure was optimised using the same settings as for the anti-conformation. The energy obtained was -231.69266120 au. As predicted the energy was larger than for the anti-conformer. The point group was said to be C₁. This was identified as the gauche conformer 3.

Re-optimization of A2 at the B3LYP/6-31G* level

The A2 conformer was re-optimized at the B3LYP/6-31G* level. The method used was modified to use DFT and the B3LYP function.. The energy of this optimization was found to be -234.61171034au. At medium constraint/default tolerance the point group was found to be C_i but at excessively loose tolerance was found to be C_2h. This molecule was found to have a higher symmetry than the previous optimization. At a glance the two structures are very similar, however on closer inspection there does appear to be some differences in bond lengths, angles and dihedral angles, which while on the surface seem to be minor, do show the effect that using different calculation methods and basis sets can make a difference to more then just the energy calculations.

While the accuracy of the calculations mean that the difference between some of the parameters are in actuality not truly valid comparisons there is one parameter that stands out as significant: the dihedral angle between hydrogens 9 and 10, as well as the slight twisting of the double bond. The anti-periplanar hydrogens deviate from 180° in one calculation and not the other because the orbitals are modeled as well as the basis sets thus which orbitals are being calculated rather then using assumed densities changes as well as to what detail the calculations are run at.

Frequency calculations and IR

In order to compare these energy values with experimentally measured quantities a frequency calculation was carried out on the re-optimized A2 (the B3LYP/6-31G*) structure to obtain more terms for the calculations. The frequency calculation was used to characterize the critical point and confirm that it is a minimum in this case. All vibrational frequencies calculated were real and positive. From these results the IR spectrum was simulated.

IR spectrum of the optimized A2 using the B3LYP/6-31G* method

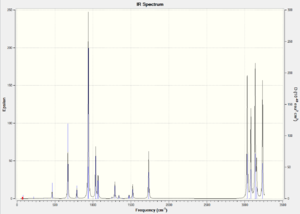
Thermochemistry

Thermochemistry calculated on this re-optimized structure at a temperature setting of 298.150 K and pressure at 1.00000 Atm.

Sum of Electronic and Zero-Point Energies	-234.469204
Sum of Electronic and Thermal Energies	-234.461857
Sum of Electronic and Thermal Enthalpies	-234.460913
Sum of Electronic and Thermal Free Energies	-234.500776

The first of these is the potential energy at 0 K including the zero-point vibrational energy (E = Eelec + ZPE), the second is the energy at 298.15 K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes at this temperature (E = E + Evib + Erot + Etrans), the third contains an additional correction for RT (H = E + RT) which is particularly important when looking at dissociation reactions, and the last includes the entropic contribution to the free energy (G = H - TS).

These calculations were re-run at 0K and the following results were produced:

Sum of electronic and zero-point Energies	-234.469202
Sum of electronic and thermal Energies	-234.469202
Sum of electronic and thermal Enthalpies	-234.469202
Sum of electronic and thermal Free Energies	-234.469202

Optimizing the "Chair" and "Boat" Transition Structures

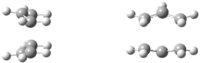
C_2h Boat Transition State

C_2v Chair Transition State Both consist of two C₃H₅ allyl fragments positioned approximately 2.2 Å apart, one with C_2h symmetry and the other with C_2v symmetry.

An allyl fragment (CH₂CHCH₂) was optimized using the HF/3-21G level of theory. This setting/basis set was used for all the following transition state calculations (unless otherwise stated). Two of these fragments were rearranged into approximate position of the chair transition state (with the two segments approximately 2.2Å part).

This transition state was optimized in two different ways. (Para on transition states)

Optimization using TS (Berny)

This transition state was Optimised to a TS (Berny) with Frequency calculations run. The force constants were set to calculate Once and Opt=NoEigen was used to stop the calculation crashing in the case were more than one imaginary frequency was detected during the optimization. This was actually unnecessary as the optimized structure was the correct chair transition state. The frequency calculation gave an imaginary frequency of magnitude 817.84 cm^-1. The results of this are summarized in a summary table below.

Optimisation using the Frozen Coordinates method

The second method is the frozen coordinate method. New vibrational calculations were run by freezing the coordinates of the terminal carbons which form/break a bond during the rearrangement and optimizing the structure to a minimum. The bond lengths between the terminal carbons were frozen to approximately 2.2Å The frequency calculation gave an imaginary frequency of magnitude 774.94 cm^-1. The two bond distances between each set of terminal carbons were 2.02063Å and 2.02068Å respectively.

QST2

QST2 method (selected using a TS (Berny) optimization) was used to optimize the boat transition state. In the QST2 method it is possible to specify the reactants and products for a reaction and the calculation will interpolate between the two structures to try to find the transition state between them.

To demonstrate the draw-backs of the QST2 method the Anti2 structure was used as a test. The following labels were used:

Reactant	Product

When the calculation linearly interpolated between the two structures, it simply translated the top allyl fragment and did not even consider the possibility of a rotation around the central bonds. The QST2 method is unable to locate the boat transition structure unless more accurate reactant and product structures are used. Although it was predicted that this calculation would fail the following molecule was produced, which clearly is not what the desired transition is:

Use of Anti2 structure

By modifying the original structures to be more like the boat transition structure a much more useful result is obtained from this calculation. The central C-C-C-C dihedral angle (i.e. C2-C3-C4-C5 for the molecule above) was changed to 0°. The inside C-C-C (i.e. C2-C3-C4 and C3-C4-C5 for the molecule above) were reduced to 100°. The reactant and product molecules had the following structuring and labeling:

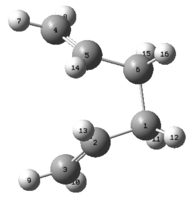
Reactant	Product

This time the calculation converged to the boat transition structure. There was only one imaginary frequency, which was at -840.04, and the IR spectrum and vibrational motion were as follows.

IR of boat Transition Structure.

Boat Transition State Animation.

File:BOAT QST2 OPTFREQ.LOG

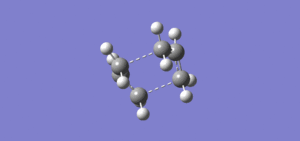
QST2 is a fully automated method that fails unless the reactants and products are close to the correct transition state.

Summary Table

Boat TS(Berny) was undertaken for comparison

Conformation/method	Chair TS (Berny)	Chair TS Frozen Coordinates	Boat TS (Berny)	Boat QST2
Imaginary frequency (Hz)	817.96	817.85	839.99
Energy (au)	-231.61932242	-231.61932232	-231.60280246	-231.60280219
RMS Grad Norm	0.00002436	0.00002313	0.00001546	0.00004199
Average Inter-fragment distance (Å)	2.021	2.021	2.140	2.141

There seems to be no significant difference between the any of methods based on the criteria above, at least at the size of system and theory level that is used.

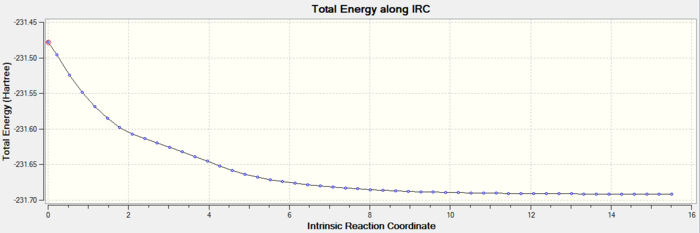
Intrinsic Reaction Coordinate

From inspection only it is impossible to predict which conformer the reaction paths from the transitions structures will lead to. Using the Intrinsic Reaction Coordinate method implemented in Gaussian it is possible to follow the minimum energy path from a transition structure down to its local minimum on a potential energy surface. This method creates a series of points by taking small geometry steps in the direction where the gradient or slope of the energy surface is steepest. Using the Berny optimised structure of the chair conformation the IRC calculations were run in the forward direction only as the reaction coordinate is symmetrical, choosing to calculate the force constants at each step. After running several test runs where the number of point taken along was altered it was settled that {300} was sufficient. This was decided as the most reliable method in this situation.

Chair IRC: We can see from the IRC output, that the structure most likely to go through this TS is the Gauche 2 structure. 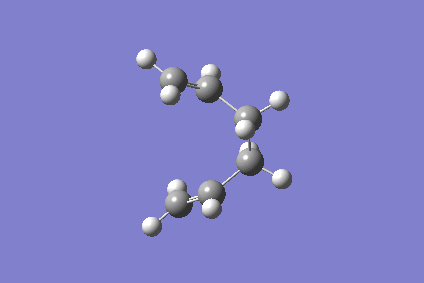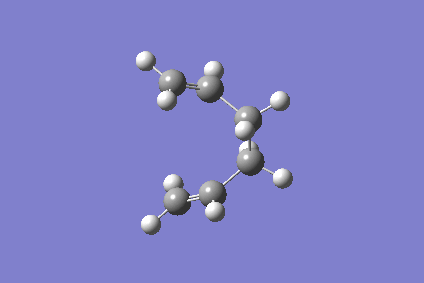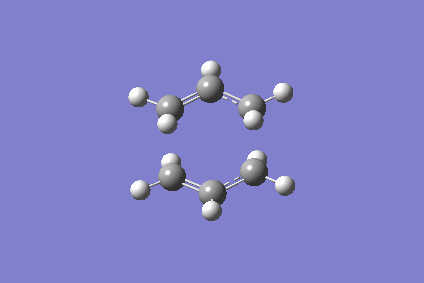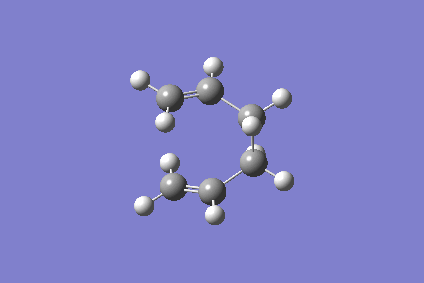File:Chair TS IRC.log

Boat IRC: The prediction from looking at the symmetries of the molecular orbitals and positions of the atoms is that for the Boat TS the structure that will undergo this transformation is the Gauche 3 structure. File:Boat TS IRC.fchk

Activation Energies

Using the relative energies of the boat and chair TS states and the structures that connect the TS's the activation energy of both transformations and the difference in energy between the two transformations can be found. First however to get more accurate values for energy, all the calculations were be recalculated using DFT/6-31G* level of theory.

	Boat	Chair
Energy	-234.54309307	-234.55693218
RMS Gradient Norm	0.00000094	0.00000062

Energy Caluclations

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Boat TS	-231.60280219	-231.450936	-231.445306	-234.54309307	-234.402342	-234.396008
Chair TS	-231.61932239	-231.466706	-231.461346	-234.55693218	-234.414879	-234.408950
anti-2	-231.69253529	-231.539540	-231.532566	-234.61171047	-234.469202	-234.461855

The Diels Alder Reaction

The Diels Alder reaction is a pericyclic reaction where the π orbitals of the dieneophile are used to form new σ bonds with the π orbitals of the diene. Whether or not the reactions occur in a concerted stereospecific fashion (allowed) or not (forbidden) depends on the number of π electrons involved. In general the HOMO/LUMO of one fragment interacts with the HOMO/LUMO of the other reactant to form two new bonding and anti-bonding MOs. Predictions are made based on the nodal properties according to the following rule: If the HOMO of one reactant can interact with the LUMO of the other reactant then the reaction is allowed and this can only happen when there is a significant overlap density. If the orbitals have different symmetry properties then no overlap density is possible and the reaction is forbidden. If the dieneophile is substituted, the interaction where π orbitals that can interact with the new double bond that is being formed in the product can stabilise the regiochemistry (i.e. head to tail versus tail to head) of the reaction. The nature of the different transition structures for the Diels Alder reaction, both for the prototypical reaction and for the case where both diene and dieneophile carry substituents where secondary orbital effects are possible, are studied. Clearly, the factors that control the nature of the transition state are quantum mechanical in origin and thus we shall use methods based upon quantum chemistry.

In the transition state the ethylene approaches the cis form of butadiene from above. The principal orbital interactions involve the π/ π* orbitals of ethylene and the HOMO/LUMO of butadiene. It is referred to as [4s + 2s] since one has 4 π orbitals in the π system of butadiene. The orbitals of ethylene and butadiene can be classified as symmetric s or anti-symmetric a with respect to the plane of symmetry shown. The HOMO of ethylene and the LUMO of butadiene are both s (symmetric with respect to the reflection plane) and the LUMO of ethylene and the HOMO of butadiene are both a. Thus it is the HOMO-LUMO pairs of orbital that interact, and energetically, the HOMO of the resulting adduct with two new σ bonds is a.

Butadiene

The structure of butadiene was optimised first at the HF/3-21G level where the energy was found to be -154.05394316 and the geometry C_2v. At the B3LYP level the energy was found to be -155.98594960 and the geometry the same as previous, C_2v. The HOMO and LUMO molecular orbitals were mapped:

LUMO	HOMO

The orbitals of ehtene were inspected in the same way:

LUMO	HOMO

From the diagrams We should expect the LUMO of the diene to interact with the HOMO of the Ethene as both are symmetric in respect to the plane perpendicular to their central bond. The HOMO with the LUMO therefore can both be allowed transitions and are antisymmetric with respect to plane.

Computation of the Transition State geometry for the prototype reaction and an examination of the nature of the reaction path.

A guess was made of the Transition state by taking the gaussian template structure of bicyclo-2,2,2-octane, removing one of the -CH2-CH2- units. The basis set used was initially HF/3-21G followed by B3LYP/6-31G*. The structure was run for Optimization and Frequency with the optimization set to a Minimum using a TS (Berny) method (the NoEigen instruction was also implemented).

HF/3-21G: When a inter-fragment distance of 2.12Å was inputted the two transition bonds were returned after the calculation as 2.20926 and 2.20911Å. However when the inter-fragment distance was estimated to be 2.2Å the calculation produced return distances of 2.20877Å and 2.20964Å. The distances are in good agreement. The energy of the 2.2Å optimized structure was found to be -231.60320841au.

B3LYP/6-31G*: From the second optimized structure an optimization using the B3LYP/6-31G* basis set the inter-fragment distances were 2.27252Å and 2.27222Å.

Lengths

Parameter	Distance
Van der waals radius of Carbon	1.7 Å
C--C Bond length	1.54 Å
C==C Bond Length	1.34 Å
TS CC distance HF/3-21G	2.21 Å
TS CC distance B3LYP	2.27 Å

From the values above it can be seen that the partially formed bond is much too long to be considered a formal bond (comparing it to the C--C and C==C bond lengths) but the fact that the distance is less then twice the van der waals radius of carbon means that is some kind of interaction taking place between the fragments.

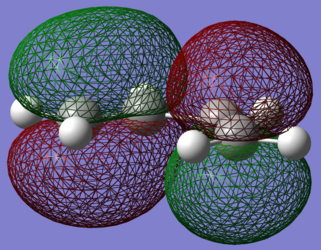
LUMO	HOMO

In the Orbital Diagram of the transition state the interaction is for the LUMO of Ethene and the HOMO of the Diene. This was expected as stability increases as conjugation increases, therefore the HOMO of Diene will have a lower energy than the HOMO of Ethene.

Study the regioselectivity of the Diels Alder Reaction

Cyclohexa-1,3-diene (1) undergoes facile reaction with maleic anhydride (2) to give primarily the endo adduct. If the reaction was kinetically controlled the exo transition state should be higher in energy.

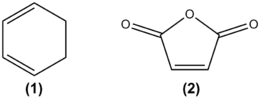
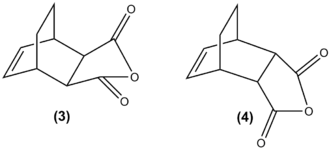
This transition state was minimized using the TS (Berny), AM1 semi-empirical molecular orbital method. The values below are from teh optimized calculations of the transition states

	Endo TS	Exo TS
Imaginary Frequency	-806.45	-812.20
Energy (au)	-0.05150475	-0.05041980 au
Inter-fragment bond lengths (Å)	2.16223 and 2.16249	2.17046 and 2.17037
LUMO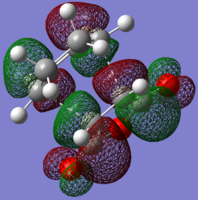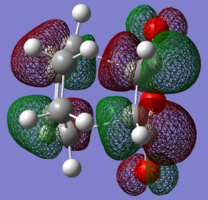
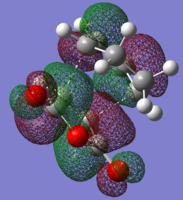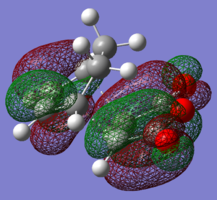
HOMO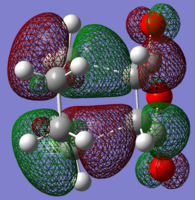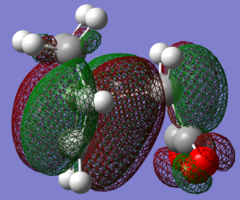
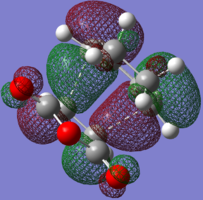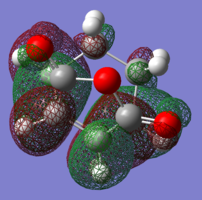
Animation
Log file	File:TS 3 AM1.LOG	File:TS 3 AM1 EXO.LOG

Possible strain seen in the endo product

Table of lengths and distances

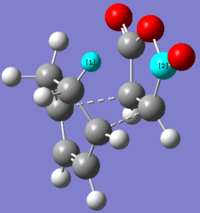
perameter	Length (Å)
Van der waals radius of Hydrogen	1.2
Van der waals radius of Carbon	1.7
Distance between H C	2.41699

What we see when looking at the distance between the Hydrogen and Carbon (indicated in the picture to the right) is that distance between the two atoms is less than the sum of their van der waals radii. It is hard to determine from just this inspect the degree to which they interact. Especially for a carbonyl carbon, there will be effects on the van der waals radius by neighboring atoms.

The oxygen in the ring of maleic anhydride will have relatively outreaching effect. There will be a through space interaction between the delocalised orbital of the double bonds of the cyclohexadiene and the carbonyl oxygens. After looking through the NBO analysis of the TS there seems to be no significant interactions between the carbonyls of maleic anhydride and the double bonds of cyclohexadiene. It is hard to tell from inspection whether lower energy MOs would have an effect on one another thus is can be concluded that this optimized structure has limited secondary orbital overlap.

Energies

Energies of Reactants, TS and Products with B3LYP/6-31G*'

	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K
Maleic anhydride	-379.28954468	-379.233654	-379.228475
Cyclohexadiene	-233.41893635	-233.296103	-233.290936
ExoTS	-612.67931095	-612.498011	-612.487664
EndoTS	-612.68339676	-612.502140	-612.491790
ExoProd	-612.75578549	-612.572069	-612.562632
EndoProd	-612.75829024	-612.569390	-612.559980

Considerations

These calculations are done as though it the components and reactantions are in a vacuum. In addition any solvent effects are neglected. This would be of use as further computational research as it has been shnown that the Diels-alder reactions takes place significantly faster with water then in organic solvents alone. If this work was further studied the effects of the aromatic ring would be taken into account. NMR could be used to do this and the shielding effects could be inspected.