Rep:Mod:LJRInorganic

EX₃ section

Structure optimisation

BH₃ optimisation

3-21G Basis set

Initally to optimise a molecule, BH₃ was optimised using the small basis 3-21G and the B3LYP method. A small basis set is a good starting point for any optimisation, as usually molecules are much larger, and the smaller basis set requires less computing power. Gaussian works by using potential energy surfaces to find a minimum in energy. The optimisation works by making an initial guess of the structure, then the program alters the structure until a stationary point of the energy is found. The optimisation data for BH₃ can be found below:

3-21G optimisation

Summary data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000216 0.000450 YES RMS Force 0.000105 0.000300 YES Maximum Displacement 0.000918 0.001800 YES RMS Displacement 0.000440 0.001200 YES Predicted change in Energy=-1.631244D-07 Optimization completed. -- Stationary point found.	Optimised BH

Results showing the convergence of the BH₃ using the 3-21G basis set

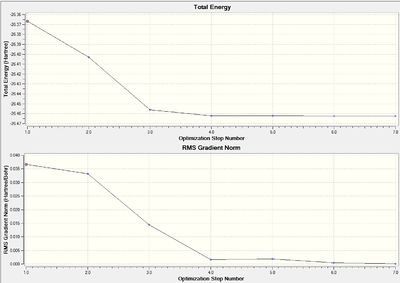
log file of 3-21G optimisation here

The results above show that the optimisation has converged, as the energy and the gradient have both decreased, showing that Gaussian has run the optimisation correctly. As can be seen from the results of the optimisation, the inital guess for the geometry of the molecule is quite good, as it only took less that 10 iterations of the algorithm before a local minimum was found. In the results graph the total energy of the graph is going down until it converges at a minimum, indicating a local minimum has been found. The bond length found in this calculation is 1.19 Å and the bond angle 120.0°.

6-31(d,p) Basis set

As the 3-21G is quite a small basis set, usually for larger molecules it is more appropriate to use a larger basis set to get a better picture of the bonding within the molecule. Once the 3-21G basis set has been used to get the molecule approximately right the better basis set can be used to improve the model, without using an excessive amount of computing power. To demonstrate this the optimised molecule of BH₃ was optimised again using the 6-31(d,p) basis set, and the results are shown below.

6-31G (d,p) optimisation

Summary data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000070 0.000450 YES RMS Force 0.000039 0.000300 YES Maximum Displacement 0.000356 0.001800 YES RMS Displacement 0.000214 0.001200 YES Predicted change in Energy=-3.183674D-08 Optimization completed. -- Stationary point found.	Optimised BH

log file of 6-31G(d,p) optimisation here

The bond angle of this molecule is 120.0°, and the bond length 1.19 Å, which is the same as was achieved before. Initially it appears that the second method has found a structure which has a lower energy as the energy from the 3-21G basis set method is -26.462 a.u. and the energy from the 6-31(d,p) optimisation is -26.615 a.u., however the two cannot be compared. Only energies from molecules optimised with the same number and type of atoms, using the same basis set and method can be compared, due to the high dependence of the energy on these variables.

Using Psuedo-potentials

The previous methods used work well for simple systems (i.e. systems that have a small number of atoms and electrons), however for larger atoms then the computing power needed to process the full wavefunction becomes too large, and in order to counteract this psuedo-potentials are used. A psuedo potential is an approximation of the core electrons of an atom, that replaces the exact Hamiltonion with a potential operator which is a close fit to the actual Hamiltonian. This is based off the common chemical interpretation that only the valence electrons are responsible for the chemistry of the molecule.

GaBr₃ optimisation

To look at how pseudo-potentials work, a molecule of GaBr₃ was optimised using the LanL2DZ basis set, which is a medium level basis set that actually uses a composite of basis sets; for the first row atoms it uses D95V, and for heavier elements it uses Los Alamos ECP, which are the psuedo potentials. Prior to the calculation the molecule was restricted to the D_3h point group, which is possible due to the small size of the molecule. The results of the calculation can be seen in the table below:

GaBr₃ optimisation run on HPC

Summary data	Convergence	Jmol
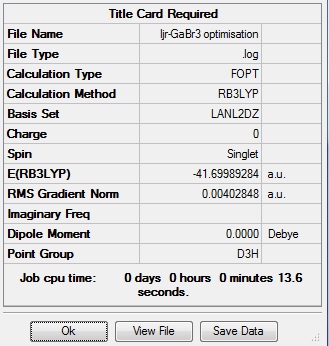	Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000003 0.001800 YES RMS Displacement 0.000002 0.001200 YES Predicted change in Energy=-1.307742D-12 Optimization completed. -- Stationary point found.	Optimised GaBr

log file of optimisation here DOI:10042/90682 It can be seen that the optimisation of the molecule of GaBr₃ has converged, indicating it has optimised. The bond length obtained is 2.35 Å and the bond angle is 120.0°.

BBr₃ optimisation

To optimise the molecule of BBr₃ the gen basis set was used, this in fact allows for the basis set for each atom to be set individually. For this molecule a full basis set (6-31(d,p)) was used on the boron atom, and psuedo-potentials (LanL2DZ basis set) were used on the bromine atoms.

BBr₃ optimisation run on HPC

Summary data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000036 0.001800 YES RMS Displacement 0.000024 0.001200 YES Predicted change in Energy=-4.086305D-10 Optimization completed. -- Stationary point found.	Optimised BBr

log file of optimisation hereDOI:10042/90686 From the optimisation files, the optimisation of the molecule appears to have converged and optimised the molecule. The bond length obtained was 1.93 Å and the bond angle is 120.0° for all bonds .

Structural comparison

geometry data

	BH3	GaBr3	BBr3
r(E-X)	1.19	2.35	1.93
θ(X-E-X)	120.0	120.0	120.0

Changing the substituent on the central atom makes the bond longer, as can be seen from the comparison between BH₃ and BBr₃, which indicated the B-H bond is much stronger than the B-Br bond. This is because although H and Br are similar in that they are both typically only able to form one bond, they differ massively in size; bromine has 35 protons and electrons, whereas an hydrogen atom only has one of each. The fact that the bromine is physically much larger means that they would be expected to be further away from each other in an equilibrium position. Additionally the proton's outer electrons are closer in energy to the Boron's than bromine and in a less diffuse orbital due to being closer to the nucleus, and this smaller energy difference and denser orbital means a stronger bond.

Changing the central atom from B to Ga also makes for a longer bond, for similar reasons that changing the substituent does. Boron and gallium are both able to form trivalent neutral species, as both lie in group 13 of the periodic table. However boron is physically a much smaller atom than gallium, therefore the equilibrium distance of the B-Br bond is much smaller than that for the Ga-Br equilibrium bond distance. Looking at the energies of the outermost electrons it might be expected that a Ga-Br bond would be stronger, as the valence electrons of bromine are closer in energy to those of gallium than boron. However it appears the size of the atom, is the determining factor in this bond length, hence the B-Br bond being stronger.

A bond is when there is an electrostatic interaction between two atoms typically caused by sharing electrons or and interaction between dipoles within molecules. A typical measure of bond strength is the bond energy, which is the average bond dissociation energy of all bonds in a specific molecule. An example of a strong bond is a N≡N triple bond, which has a bond energy of 946 kJmol^-1 , a weak bond strength would be that of a hydrogen bond which is around 15 kJmol^-1 and finally a medium bond strength would be a C-C bond which has a bond strength of 348 kJmol^-1 . In some structures Gaussian does not draw the expected bonds, due to the fact that it uses a distance algorithm to determine which atoms are bonded to each other. This doesn't neccessarily mean that there isn't a bond, as there could be a very weak bond, that falls outside the parameters of the algorithm, equally two atoms could be very close together and not bonded, but Gaussian could misinterpret this and draw a bond.

Frequency Analysis

BH₃

In order to determine whether the stationary point found by the program in the optimisation step above is a minimum, frequency analysis must be performed on the molecule. Frequency analysis calculates the force constants and therefore the vibrations of a molecule and their infrared intensities by computing the second derivatives of the energy curve. If all vibrations obtained are real then a minimum has been found, and the optimised structure is correct and not simply a transition state. A frequency analysis must be carried out using the same method as the optimisation to fully be able to talk about the two together, therefore the frequency analysis was run using the B3LYP method and the 6-31(d,p) basis set. The table below shows the summary data and the low frequencies obtained, which since all are between ±15 cm^-1 shows the frequency analysis has confirmed the structure found is a minimum. The low frequencies show the motion of the centre of mass of the molecule, and should be as close to zero as possible, as the better the optimisation the closer to zero the low frequencies will be.

BH₃ frequency

Summary data	Low modes
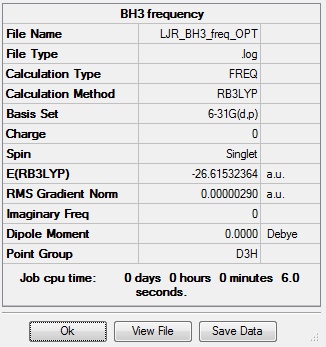	Low frequencies --- -12.4451 -12.4386 -7.8187 0.0008 0.0234 0.4030 Low frequencies --- 1162.9687 1213.1351 1213.1353

Frequency log file here.

Aditionally the vibrations were examamined, and can be seen in the table below and the IR spectrum was also computed from these vibrations and appears below the table.

Frequency data

Wavenumber (cm-1)	Intensity	IR active?	Type
1163	93	Yes	bend
1213	14	Slightly	bend
1123	14	Slightly	bend
2582	0	no	stretch
2716	126	yes	stretch
2716	126	yes	stretch

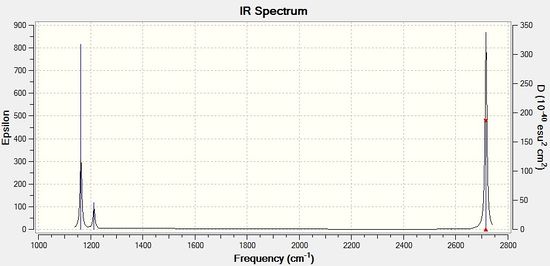
There are 6 vibrations that this molecule undergoes, this corresponds correctly to the 3N-6 rule, where N=4 here. Some peaks are degenerate as the mode of vibration produces the same change in dipole moment, due to the high level of symmetry within this molecule, so these peaks appear superimposed. Additionally some peaks are not IR active, as they do not involve a change in dipole moment, which is required for IR spectroscopy. Therefore the are less than the six expected peaks, due to degeneracy of vibrations, and non IR active vibrations. The difference in intensity is related to change in dipole moment, the less intense peaks have a smaller change in dipole moment, and so are less visible than others.

GaBr₃

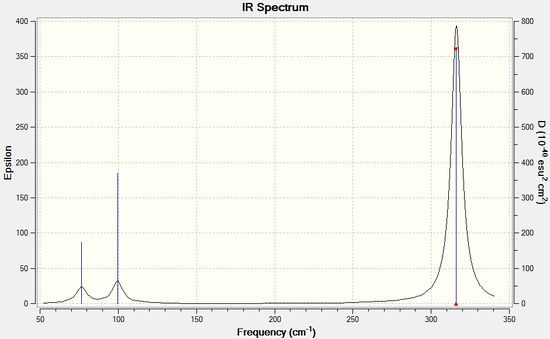
The same frequency analysis was performed on GaBr₃, once again to determine that the structure found is a minimum point. The frequency analysis was carried out using the same method and basis set as the optimisation, i.e. B3LYP method, and 6-31(d,p) basis set, and the results can be seen in the tables and IR spectrum below. The low frequencies are all within ±15 cm^-1, showing no imaginary vibrational frequencies have been found, so the structure is a minimum on the potential energy surface. Additionally the number of vibrations is again correct for the number of atoms present, with some degenerate and non IR active vibrations.

GaBr₃ frequency

Summary data	Low modes
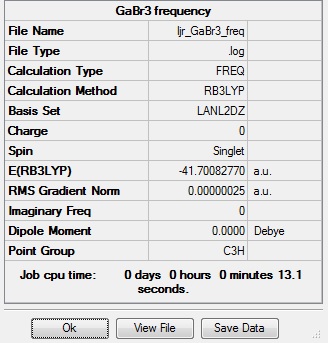	Low frequencies --- -1.4878 -0.0015 -0.0002 0.0096 0.6540 0.6540 Low frequencies --- 76.3920 76.3924 99.6767

Frequency data

Wavenumber (cm-1)	Intensity	IR active?	Type
76	3	Slightly	bend
76	3	Slightly	bend
100	9	Slightly	bend
197	0	no	stretch
316	57	yes	stretch
316	57	yes	stretch

Vibrational analysis files here: DOI:10042/90883

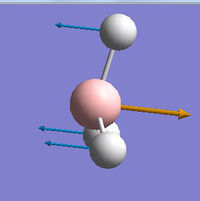
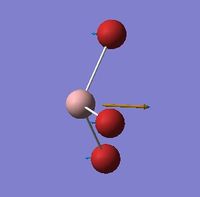
Comparison of vibrational analysis of BH₃ and GaBr₃

The frequency of vibrations differs massively between the molecule, with the BH₃ vibrations in the range 1163-2716 cm^-1 and the GaBr₃ vibrations in the range 76-316 cm^-1. The large difference is a result of the difference in mass between the two molecules. Vibrational frequency is inversely proportional to the square root of the mass of the molecules involed, and as both gallium and bromine are much larger atoms than either boron or hydrogen, it is not unreasonable that the GaBr vibrations are at much lower frequencies. Between the two molecules there has been a reordering of modes, for instance the A2'' umberella mode has the lowest frequncy vibration in BH₃, but the highest frequency bending mode in GaBr₃. This is likely due to the mass difference between the two molecules. Additionally it can be seen that the movement of the hydrogen atoms is much greater than the bromine atoms for the same vibrational mode. This is because the hydrogens are considerably lighter, and thefore less energy is needdd to make them to move further. However both atoms have the same modes which are IR active, due the fact that they have the same symmetry.

A2'' umberella bending mode comparison

BH3	GaBr3

Determining BH₃ MOs

The molecular orbitals of the optimised molecule were computed using the B3LYP method and the 6-31(d,p) basis set, and can be seen on the molecular orbital diagram drawn below next to the energy level that they correspond to. The full .log and .fchk files can be found at DOI:10042/90920

MO diagram of a BH₃

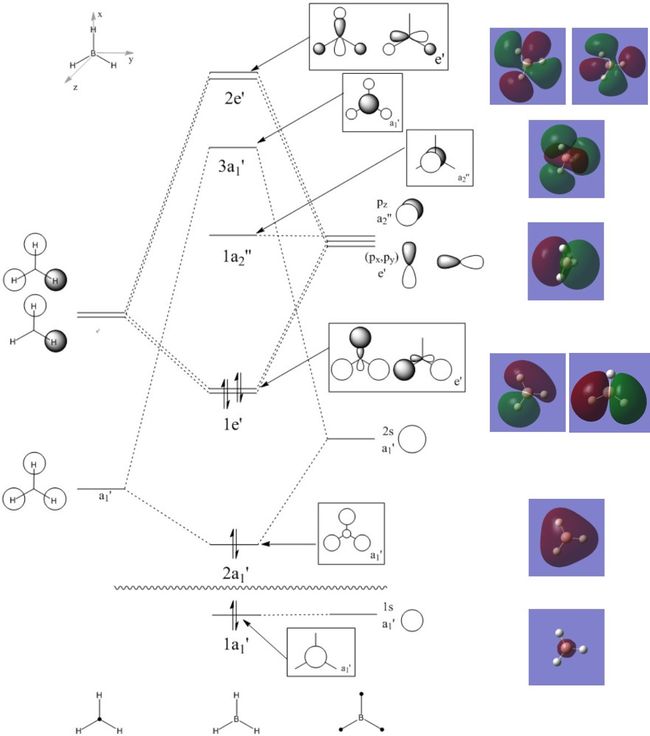
Looking at the MOs calculated, the unoccupied MOs are much more diffuse than the occupied ones, and have stranger forms than the occupied ones. The LUMO of this molecule is a p orbital that hasn't mixed with any from the H₃ fragment, as none of the other fragments have the correct symmetry, also HOMOs of this molecule are degenerate e' orbitals. It appears that all MOs calculated appear to be similar to those drawn, with only slight differences in the contributions from each atom. This shows that the MO calculation is fairly good for this molucule. Of course this is a small molecule, and the model may break down with larger molecules due to the complexity and the computing power require. Therefore the accuracy cannot be stated for all sizes from this sample, although its accuracy is a good indicator that the model is good, and could work for larger molecules.

NH₃ Optimisation, Frequency analysis, MO detemination and NBO analysis

Optimisation

The molecule of NH₃ was optimised using the B3LYP method and the 6-31(d,p) basis set as before, to produce the molecule shown below. The optimisation was completed correctly as all optimisations converged. The bond length calculated is 1.02 Å, and has a bond angle of 107.5°, which corresponds to the literature values of... respectively. The bond angle shows that there is a slight deviation from the perfect sp³ hyrbidised bond angle of 109°, which is due to the lone pair on the nitrogen atom repelling the bonding pairs more than a bonding pair would.

NH₃ optimisation

Summary data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000012 0.001800 YES RMS Displacement 0.000008 0.001200 YES Predicted change in Energy=-9.843884D-11 Optimization completed. -- Stationary point found.	Optimised BBr

Optimisation log file can be found here

Frequency analysis

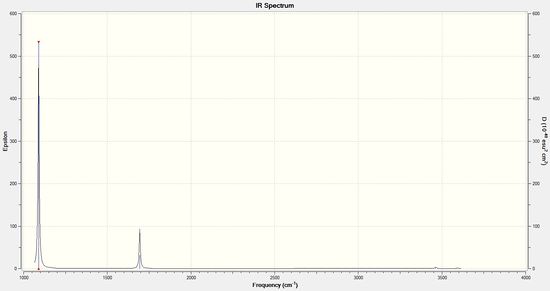
Frequency analysis was used to determine that the stationary point found in the above optimisation is indeed a minimum energy point. As the low modes are all within ±15 cm^-1, the program has indeed found a minimum energy point, and thus the equilibrium structure of NH₃. There are the expected 6 vibrations in this molecule; all of the bending modes are IR active, wheras none of the stretching modes are IR active. This is different to the vibrations of the molecules of GaBr₃ and BH₃, which is likely due to the fact that NH₃ has a different symmetry than those molecules.

NH₃ Frequency analysis

Summary data	Low modes
	Low frequencies --- -0.0138 -0.0026 -0.0008 7.0783 8.0932 8.0937 Low frequencies --- 1089.3840 1693.9368 1693.9368.

Frequency data

Wavenumber (cm-1)	Intensity	IR active?	Type
1089	145	Yes	bend
1694	14	Yes	bend
1694	14	Yes	bend
3461	1	Extremely slight	stretch
3590	0	Extremely slight	stretch
3590	0	Extremely slight	stretch

Frequency Log file can be found here

MO detemination and NBO analysis

The molecular orbital file can be found at this link DOI:10042/93500

Charge distribution of NH₃ using the colour range -1.125 to 1.125

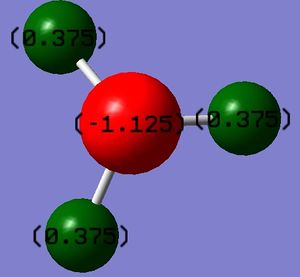
The charge distribution of this molecule shows the nitrogen atom as highly negatively charged and the hydrogen atoms as highly positive, this expected as nitrogen is highly electronegative, so the majority of the electron density should be on the nitrogen atom.

Looking at the NBO analysis of the NH₃ molecule, it can be seen that for the N-H bonds the nitrogen contributes 69% (of which 25% is from a s orbital and 75% from p orbitals), and the hydrogen contributes 31%. This NBO occupancy shows that the nitrogen forms four sp³ hybridised orbitals to from a bond with the hydrogen atoms and contain the lone pair. The final bonding orbital is the core 1s atomic orbital on the nitrogen atom. Additionally the NBO analysis shows that there is no mixing of MOs occuring in this molecule. Finally from the natural bond orbitals summary it can be seen that the core atomic orbital of the nitrogen is much deeper in energy than the valence bonding orbitals, which is why they are usually not included in bonding considerations.

BH₃NH₃

A molecule of BH₃NH₃ was optimised using the B3LYP method and the 6-31(d,p) basis set, and the following molecule was obtained. Frequency analysis was also carried out with the same method and basis set to confirm a minimum was obtained, and since all low modes obtained are within +/-5 cm^-1, the molecule has be successfully optimised. These are small low modes indicating a good optimisation was achieved.

BH₃NH₃ optimisation

Summary data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000001 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000008 0.000060 YES RMS Displacement 0.000004 0.000040 YES Predicted change in Energy=-9.612817D-12 Optimization completed. -- Stationary point found.	Optimised BBr

optimisation log file can be found here.

BH₃NH₃ Frequency analysis

Summary data	Low modes
	Low frequencies --- -0.1135 -0.0485 -0.0214 2.5528 2.7328 4.4823 Low frequencies --- 263.3711 632.9789 638.4939

Frequency log file can be found here

The total energy change in formation of B-N bond can be calculated by taking the energies of the separate molecules (Calculated previously) from the energy of the molecule. In order for these to be directly comparable the same method and basis set were used in all calculations.

ΔE=E(NH₃BH₃)-[E(BH₃)+E(NH₃)]

E(NH₃)= -56.558 a.u. E(BH₃)= -26.615 a.u. E(NH₃BH₃)= -83.225 a.u.

ΔE = -83.225 + (26.615+56.558)

ΔE = -0.052 a.u.

=-136 kJmol^-1

This is a weak-medium strength bond which would be expected as it is not a full covalent bond, only a dative bond (which are usually weaker), and it falls within the accepted range of bond strengths. It is in the same region as the literature value of -115kJmol^-1 . The slight error is due to the error on the calculations, and deviations from ideality caused by using a basis set that isn't as good as is typically needed for a molecule of this size.

Ionic Liquids

Introduction

An ionic liquid is a liquid that consists solely of ions. These have many applications particularly as solvents, and many are proposed to be more environmentally friendly than traditional solvents and it is possible to fine tune the structure of the anion and cation of an ionic liquid in order to produce a range of properties. To try all the combinations experimentally would be time consuming and a waste of resources, so to combat this problem many researchers are now using computational chemistry to probe the structures of anions and cations as a time saving method. . In this project the aim is to investigate five cations by optimising their structure and performing a natural bond analysis to elucidate the properties of the cations.

'Onium' Cations

Optimisation, frequency and NBO/MO analysis of N(CH₃)₄⁺

The molecule of N(CH₃)₄ was optimised using the B3LYP method and the 6-31G(d,p) basis set. This gave a bond length of 1.51 Å for the N-C bonds, and 1.09 Å for the C-H bonds. Additionally the bond angle is 109.5° between each methyl group on the Nitrogen atom, 108.9° between a hydrogen and the nitrogen, and 110.0° between hydrogens. This suggests perfect sp³ hybridisation at the nitrogen centre, but a slight distortion at the carbon.

N(CH₃)₄⁺ optimisation

Summary data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000072 0.000450 YES RMS Force 0.000028 0.000300 YES Maximum Displacement 0.000614 0.001800 YES RMS Displacement 0.000166 0.001200 YES Predicted change in Energy=-9.927304D-08 Optimization completed. -- Stationary point found.	Optimised BBr

Optimisation log file here DOI:10042/101518

Additionally to check the stationary point found is a minimum and not simply a transition state, a frequency analysis was run with the B3LYP method and 6-31(d,p) basis set as usual. As the low modes of the frequency analysis are within +/- 15cm^-1, a minimum has been obtained. Additionally the molecule has the expected 3N-6 vibrations (N=17), however there are too many to go into a detailed analysis.

N(CH₃)₄ Frequency analysis

Summary data	Low modes
	Low frequencies --- -0.0006 -0.0004 0.0008 6.4137 7.3588 11.9743 Low frequencies --- 186.0203 290.0941 290.9446

DOI:10042/101512

Additionally a full MO and NBO analysis was run, and the file can be found here. DOI:10042/101696

The NBO analysis of the charge distribution shows that the carbon atoms are highly negatively charged whereas, the Nitrogen atom has less negative charge than the carbon. This is due to the fact that it is usually a trivalent atom, however here it has four groups.

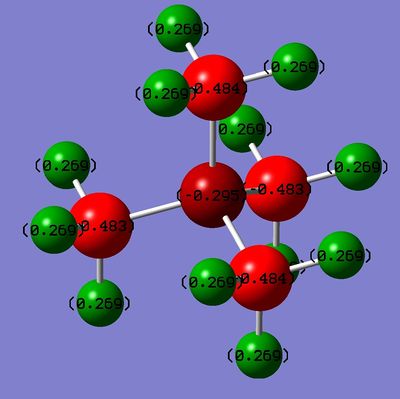
Charge distribution of N(CH3)4+ using the colour range -0.483 to 0.483

In order to get a general idea of the molecular orbitals of N(CH₃)₄⁺ five occupied molecular orbitals were visualised and analysed. It should be noted that the size of the orbital in the sketches unless mentioned has no bearing on the actual contribution of each atom to the orbital, as this is difficult to calculate without drawing a full MO diagram. Additionally, due to the shape of the molecule it is difficult to draw the groups properly orientated, so the orbital diagrams are merely to show which orbitals are involved and what interactions are present. The interactions are annotated with ts or tb (through space or through bond) and bonding or antibonding (b or ab). Finally the molecular orbitals aren't perfect, as the molecule wasn't constrained to a specific symmetry, because it is too large, therefore the loss in symmetry causes some of the orbitals to be a little different from theory.

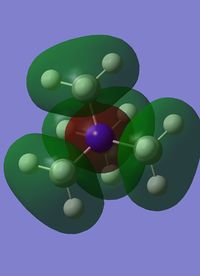
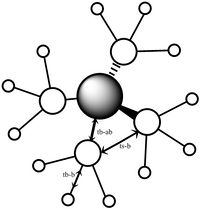
Molecular orbital number six is the first non core orbital is a totally bonding orbital made up of s orbital from the nitrogen, carbon and hydrogen atoms, with the largest contribution from the nitrogen atom, hence the fact that most of the orbital seems slightly contracted to the nitrogen. As it is a completely bonding orbital there are no nodal planes. The hydrogens only contribute a very small amount, much less than the carbons. The interactions between the s orbitals are through bond and through space, and overall this molecule has a very strong bonding character.

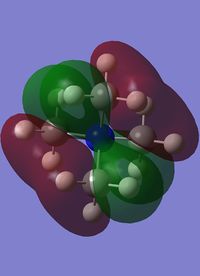
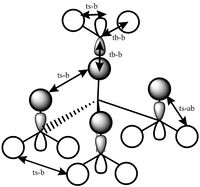
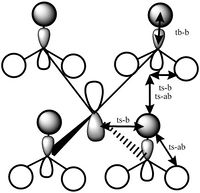
Orbitals 7-9 are all degenerate, as they are simply the same orbital made from different p orbitals from the nitrogen. These are formed from a p orbital on the nitrogen, and a totally bonding fragment from each methyl group made up of s orbitals, two in phase and two out of phase, matching with the p orbital. There is strong through bond bonding character on the methyl group orbital. There is also medium strength through space bonding between the lobe of the p orbital from the nitrogen and the atomic orbitals of the methyl. There is a weak antibonding though space bonding character between methyl groups. One nodal plane exists between the two separate parts, cutting the nitrogen atom in half. This orbital has strong bonding character despite the antibonding through space interactions.

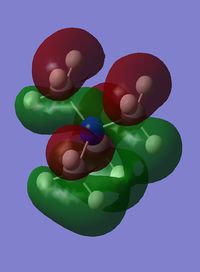
Orbital 10 is made up of s orbitals from all the atoms, however the methyl groups are not in phase with the nitrogen s orbitals. Therefore this orbital has strong through bond bonding components in the methyl fragments, and strong through bond anti bonding components through the N-C bond. It also has weaker through space bonding between the methyl groups. This means that overall this orbital is bonding despite the strong antibonding components.

Orbital 14 contains only components from the methyl groups and none from the central nitrogen atoms. It is a combination of the p orbital from the carbon atoms and the s orbitals from hydrogen atoms. There are through space bonding interactions between the methyl groups, which results in essentially 3 ring like orbital lobes which can be seen in the orbital calculation, so there are 2 nodal planes between these rings. There are then antibonding interactions between the rings, as there is one out of phase ring between two that are in phase with each other, resulting in a lot of antibonding interactions. However overall, this orbital has majority bonding character.

Orbital 21 is the HOMO of the molecule,and is made of components from all the atoms in the molecule. It is made up of the p orbitals from the nitrogen and carbon atoms and the s orbitals from the hydrogen atoms. There are many interactions in this orbital, there are through space antibonding between s orbitals within a methyl groups and between methyl groups. There are also through space bonding interactions between the s orbitals and p orbital lobes on the nitrogen, and the p orbital lobes on the carbon. Due to its complex shape there are no nodal planes in this orbital.

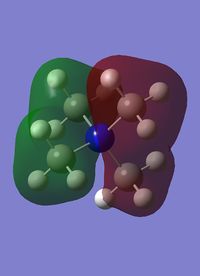MO 6	MO 7	MO 10	MO14	MO 21

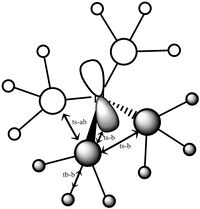Optimisation and frequency analysis of P(CH₃)₄⁺

The molecule of P(CH₃)₄ was optimised using the B3LYP method and the 6-31G(d,p) basis set. This gave a bond length of 1.82 Å for the P-C bonds, and 1.09 Å for the C-H bonds. Additionally the bond angle is 109.5° between each methyl group on the phosphorus atom, 109.9° between a hydrogen and the phosphorus, and 109.0° between hydrogens. This once again suggests perfect sp³ hybridisation at the phosphorus centre, but an even smaller slight distortion at the carbon than the N(CH₃)₄⁺. A frequency analysis was also carried out and since all the low frequencies are between +/- 20 cm^-1 then it can be said that a minimum has been found as there are no imaginary frequencies of vibrations.

P(CH₃)₄⁺ optimisation

Summary data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000039 0.000450 YES RMS Force 0.000013 0.000300 YES Maximum Displacement 0.000354 0.001800 YES RMS Displacement 0.000107 0.001200 YES Predicted change in Energy=-2.696085D-08 Optimization completed. -- Stationary point found.	Optimised BBr

DOI:10042/104584

P(CH₃)₄⁺ frequency analysis

Summary data	Low Modes
	Low frequencies --- -0.0019 -0.0004 0.0019 5.1097 7.8520 18.3121 Low frequencies --- 158.0487 193.4420 193.5952

DOI:10042/104603

MOs and NBO files: DOI:10042/104611

Optimisation and frequency analysis of S(CH₃)₃⁺

The molecule of S(CH₃)₃ was optimised using the B3LYP method and the 6-31G(d,p) basis set. This gave a bond length of 1.82 Å for the S-C bonds, and 1.09 Å for the C-H bonds. Additionally the bond angle is 102.7° between each methyl group on the sulphur atom, 107.3° between a hydrogen and the sulphur, and 109.4° between hydrogens. This suggests that the sulphur is not sp₃ hybridised, and hence the distortion that appears at the sulphur centre. Vibrational analysis was carried out and it was determined that the low frequencies were small enough, and so a minimum had been found and not a transition state.

S(CH₃)₃⁺ optimisation

Summary data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000011 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000968 0.001800 YES RMS Displacement 0.000298 0.001200 YES Predicted change in Energy=-8.903666D-09 Optimization completed. -- Stationary point found.	Optimised S(CH(

DOI:10042/104616

S(CH₃)₃⁺ frequency analysis

Summary data	Low Modes
	Low frequencies --- -7.0529 -2.6441 -0.0045 -0.0042 -0.0011 2.4059 Low frequencies --- 161.7253 199.2052 199.9194

DOI:10042/104621

MOs and NBO: DOI:10042/104623

Discussion of geometry and charge distribution of 'onium ions'

geometry data

	N(CH3)4+	P(CH3)4+	S(CH3)3+
r(E-C)	1.51	1.82	1.82
r(C-H)	1.09	1.09	1.09
θ(C-E-C)	109.5	109.5	102.7
θ(E-C-H)	108.9	109.9	107.3
θ(H-C-H)	110.0	109.0	109.4

From the geometries above it can be seen that the central atoms in both N(CH₃)₄⁺ and P(CH₃)₄⁺ cations both have ideal sp³ hybridisation at the central atom, wheras the S(CH₃)₃⁺ centre is distorted significantly. Additionally the carbon centres are also not ideally sp³ hybridised, and also appear to have different bond angles to the central atom than between the hydrogens, indicating different types of bonding orbital.

Looking at the NBO analysis from each molecule it can be seen that both the nitrogen atom and the phosphorus atom hybridise to form 4 sp³ orbitals in order to bond with the carbon atoms, this is expected of atoms from group 15. However it appears that the sulphur atom is different; it also hybridises its s and p orbitals, however not in an sp³ manner. To form the orbital that contributes to the S-C bond the sulphur atom contributes 17% from s orbitals and 82% from p orbitals (and 1% from d orbitals) and the carbon atom produces an orbital where 20% is contributed from s orbitals and 80% from p orbitals. This would explain the deviation from the 'ideal' sp³ bond angles that appeared before. This is a similar orbital style to that of water, which has 80% p character for the bonding orbitals, and in order to compensate the orbital containing the lone pair takes on a greater s character than the other bonding orbitals; the same thing is true of this molecule where the orbital containing the lone pair has 49% s character and 51% p character. The similar bonding style is expected due to the fact that oxygen and sulphur are in the same group of the periodic table. So using the equation to define formal hybridisation 1+n(cosθ)=0 (where n is the proportion of contribution from the p orbital), it can be described at sp^4.5 . These deviations from 'ideal' hybridisation indicate that hybridisation is not the best model to use, as sp^4.5 means very little in real terms and this shows the breakdown of hybridisation as a model to describe bonding. Therefore it is much more appropriate to talk about molecular orbitals in these calculations.

The bond length of the N-C bond is much shorter than the P-C, and S-C bonds, meaning that it has formed a stronger bond. This is because the nitrogen's outer orbitals (2p orbitals) are more similar in energy to carbon's outer orbitals which are also 2p orbitals, this close match in energy makes for a strong bond, and a shorter bond length. However sulphur and phosphorus's outer orbitals are 3p orbitals which are not as close in energy, so there is an energy mismatch resulting in a longer bond. Additionally nitrogen is a smaller atom than both sulphur and phosphorus and will lie at equilibrium closer to the carbon than the other two atoms. The S-C bond and P-C bond are so similar because the two atoms are next to each other in the periodic table, meaning only a small size and energy difference.

Charge distribution

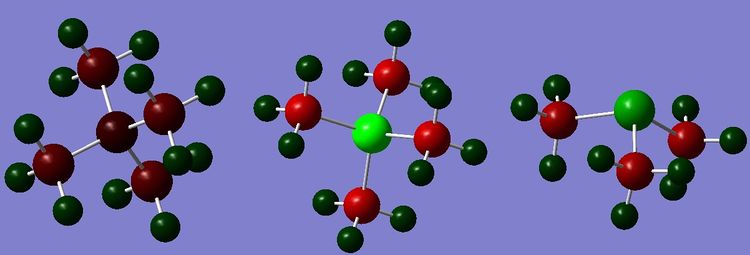
Charge distribution of N(CH3)4+, P(CH3)4+ and S(CH3)3+ shown by the colour range -1.667 to 1.667
N(CH3)4+		P(CH3)4+		S(CH3)3+
N	-0.259	P	1.667	S	0.917
C	-0.484	C	-1.060	C	-0.846
H	0.269	H	0.298	H	(Up) 0.279 (down) 0.297

The charge distribution from the NBO analysis of the 3 cations can be seen above, and it appears that the most remarkable difference is in the charge on the central atom. As all of the molecules have a formally positive charge, so it is expected that the central atom will have less of negative charge than would be expected if there was no charge. Nitrogen is the most electronegative atom of all the three centres, and therefore it is the only one to have retained a negative charge- despite the fact that it is less negative than the carbon, which looking at electronegativity values alone would not be expected. Sulphur is the next most electronegative of the three, and has an electronegativity which is the same as carbon, so looking only at the electronegativity values alone the two atoms would be expected to have the same charge. However due to having a formally positive charge, sulphur has a more positive charge than that of the carbon. The least electronegative is phosphorus, so following the arguments from the previous two molecule, it has a very positive charge distributed on its centre. It is interesting to note that since the molecule in the calculation is static then due to the tripod like structure the hydrogens pointing upwards (i.e. towards the sulphur atom) are more positive than the ones pointing away.

Traditionally the formal charge would be placed on the central atom, as this is the atom with more than its usual valency. Looking at the charge distribution this can be rationalised by the fact that the central atom is holding less of the electrons that would usually be expected by looking at electronegativity values, and in fact for P(CH₃)₄⁺ and S(CH₃)₃⁺, the majority of the positive charge is based on the central phosphorus atom. However in N(CH₃)₄⁺ the positive charge is on the hydrogen atoms, but the formal charge is placed on the nitrogen, as normally it would be expected to be much more negative than it is.

Additionally it should be noted that in the N-C bonds the nitrogen atom contributes 66% to the bond, in the P-C bond the phosphorus atom contributes 40%, and in the S-C bond the the sulphur atom contributes 51%. The contributions can be put down to the relative electronegativities between the two atoms. Sulphur has similar a similar electronegativity to carbon with carbon having a pauling electronegativity of 2.55 and sulphur an electronegativity of 2.58, therefore both contribute relatively equally. Nitrogen has a considerably larger electronegativity that carbon (3.04), so it contributes much more to a N-C bond, and phosphorus has a lower electronegativity than carbon (2.34) so contributes less to the bond than carbon.

Effect of Functional groups

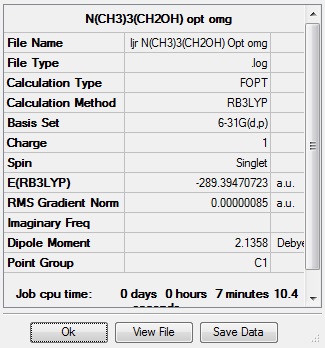
Optimisation and frequency analysis of N(CH₃)₃(CH₂OH)⁺

A molecule of N(CH₃)₃(CH₂OH)⁺ was optimised using the B3LYP method and the 6-31(d,p) basis set, to produce the molecule shown below, and a frequency analysis was carried out to confirm that a minimum had been obtained. All the low frequencies are between +/-10 cm_-1, therefore the stationary point obtained is a minimum. What is interesting about this molecule is that if the optimisation is set to run with the initial guess placing the proton on the oxygen trans to the nitrogen, then the stationary point found is a transition state, as it cannot move past the steric restriction of the hydrogens on the CH₂ group. However if the optimisation is run with the two groups cis, then a minimum is found.

N(CH₃)₃(CH₂OH)⁺ optimisation

Summary data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000003 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000054 0.000060 YES RMS Displacement 0.000014 0.000040 YES Predicted change in Energy=-1.294889D-10 Optimization completed. -- Stationary point found..	Optimised S(CH(

Optimisation files can be found here DOI:10042/110656

N(CH₃)₃(CH₂OH)⁺ frequency analysis

Summary data	Low Modes
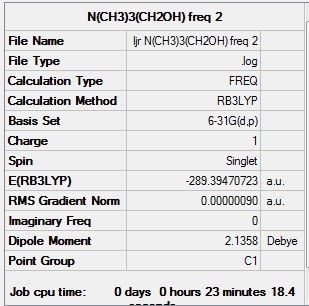	Low frequencies --- -7.0529 -2.6441 -0.0045 -0.0042 -0.0011 2.4059 Low frequencies --- 161.7253 199.2052 199.9194

Frequency log file here DOI:10042/110659 10042/110659

MOs and NBO files here DOI:10042/110661 10042/110661

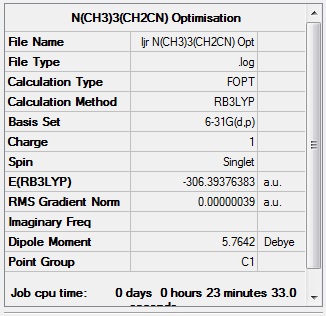
Optimisation and frequency analysis of N(CH₃)₃(CH₂CN)⁺

The molecule of N(CH₃)₃(CH₂CN)⁺ was optimised using the B3LYP method and the 6-31(d,p) basis set. The molecule optimised and a frequency analysis was run using the same method and basis set, and confirmed that a minimum had been obtained.

N(CH₃)₃(CH₂CN)⁺ optimisation

Summary data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000000 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000060 0.000060 YES RMS Displacement 0.000013 0.000040 YES Predicted change in Energy=-1.659110D-11 Optimization completed. -- Stationary point found.	Optimised S(CH(

Optimisation log file here DOI:10042/104832

N(CH₃)₃(CH₂CN)⁺ frequency analysis

Summary data	Low Modes
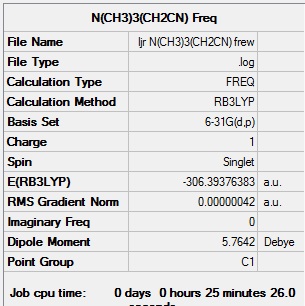	Low frequencies --- -2.6078 0.0005 0.0007 0.0011 7.1507 9.6733 Low frequencies --- 91.7744 154.0284 210.9296

Frequency log file here DOI:10042/104834

MOs and NBO files here DOI:10042/104839

Discussion

geometry data

N(CH3)3(CH2OH)+		N(CH3)3(CH2CN)+
r(Ncentral-C)	1.50 (to methyl groups) 1.55 to CH2OH	r(Ncentral-C)	1.51 (to methyl groups) 1.53 to CH2CN
r(C-H)	1.09	r(C-H)	1.09
r(C-O)	1.37	r(C-C)	1.46
r(O-H)	0.97	r(C≡N)	1.16
θ(C-N-C)	(C1-N-C2) =108.4 (C2-N-C3) =110.1 (C3-N-C4) =109.6 (C1-N-C4) =109.8 (C1-N-C3) =108.7 (C2-N-C4) =110.1	θ(C-N-C)	C1-N-C2) =110.1 (C1-N-C3) =108.0 (C1-N-C4) =110.1 (C2,2,3-N-C3,4,4) =109.5
θ(N-C-H)	(N-C2,3,4-H)= 108.5-109.6 (N-C1-H)= 105.0 and 106.0	θ(N-C-H)	(N-C2,3,4-H)= 108.3-109.1 (N-C1-H)= 107.8
θ(H-C-H)	109.7-110.7	θ(H-C-H)	(C2,3,4) 109.9 -110.3 (C1)108.8
θ(C-O-H)	111.4	θ(C-C-N)	178.8

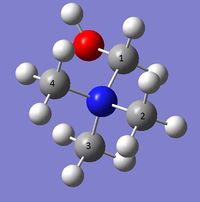
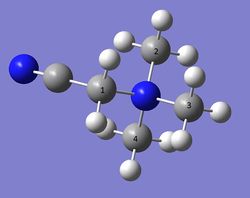It is difficult to tell anything particular from the bond angles, as they are quite different. However looking at the NBO bond orbitals, it can be seen that the nitrogen has sp³ hybridised orbitals which bond to all the carbons in both molecules with only slight deviations. Additionally in the OH and CN compound the nitrogen contributes 66-67% of the N-C bond, this is due to the higher electronegativity of nitrogen in comparison to carbon. This is the same as for N(CH₃)₄, and has not been changed by the functional groups. These molecule have very little symmetry due to the functional group on one of the carbon atoms. The N_central-C bond length is around 1.50-1.51 Å to the methyl groups, however adding a functional group makes the bond length to the carbon with the functional group attached to slightly longer. This is because the bond strength is reduced, because some of the electron density is shared with the functional group, which takes a larger share than a hydrogen, which makes the C-N bond weaker.

Homo and Lumo comparison

	HOMO	LUMO	HOMO- LUMO energy levels	HOMO-LUMO gap/kJmol-1
N(CH3)3+		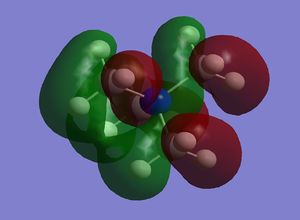		280
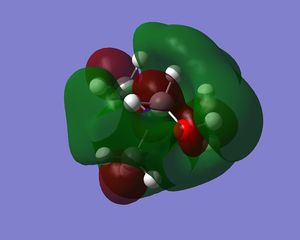
N(CH3)3(CH2OH)+		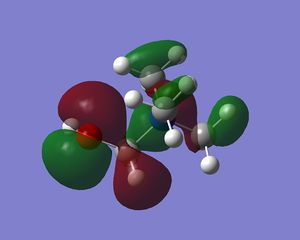		230
N(CH3)3(CH2CN)+		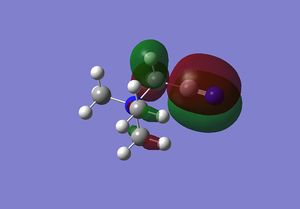		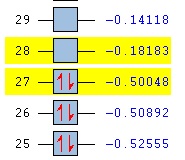200

On N(CH₃)₄ the orbitals are diffuse, and aren't centred anywhere in particular, and adding a functional group to one carbon makes the HOMO a lot more contracted, and the majority of the molecular orbital is focused on the carbon near to the functional group, and on the functional group itself. Adding the OH group, increases the energy of the HOMO as it is an electron donating group, and adding electron density makes it easier to remove electrons. In contrast adding an electron withdrawing group (CN) has lowered the energy of the LUMO as it is now easier to add electrons to the molecule. The LUMOs of the molecules with the functional groups are again less diffuse that the N(CH₃)₄⁺ LUMO, with N(CH₃)₃(CH₂CN)⁺ being the most contracted- meaning it is easier to add electrons to the system than the other molecules. The HOMO-LUMO gap on the molecule containing the OH group is larger than that of the cation containing the CN group; the energy difference is 230 kJmol^-1 and 200 kJmol^-1 respectively, and both of these are smaller that the HOMO LUMO gap in N(CH₃)₄⁺ which has an energy gap of 280 kJmol^-1. This means that it is easier to promote the electrons to the excited state in the molecules with the functional groups.

Typically functionalised ionic liquids can be used to act as acids and bases, which has a particular use in catalysis, replacing traditional acids.. All cations act as Lewis acids as they are able to accept electrons, therefore comparing the energy of the LUMO will indicate which of these molecules act as the best Lewis acid- the lower in energy the LUMO is the better Lewis acid it is. This makes N(CH₃)₃(CH₂CN)⁺ the best Lewis acid, because as discussed before it has the lowest LUMO, meaning that it is the easiest to add electrons to, making it a good lewis acid. This is an example of using computational chemistry to elucidate properties of an ion in an ionic liquid.

Charge distribution

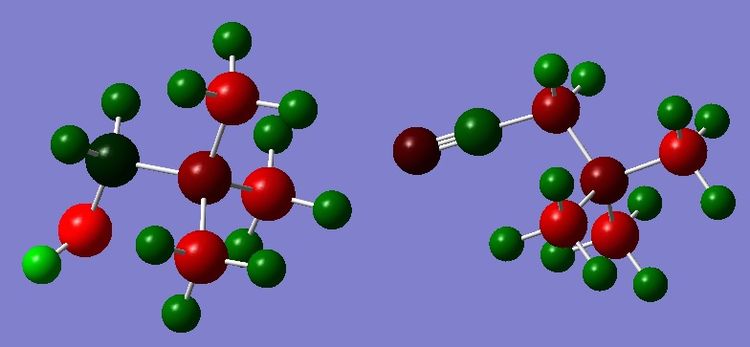
Charge distribution of N(CH3)3(CH2OH)+ and N(CH3)3(CH2CN)+ shown by the colour range -0.725 to 0.725
N(CH3)3(CH2OH)+		N(CH3)3(CH2CN)+
Ncent	-0.322	Ncent	-0.289
C1	0.088	C1	-0.358
C2,3,4	-0.491 to -0.494	C2,3,4	-0.489
(C2,3,4) H	0.262 to 0.274	(C2,3,4) H	0.269-0.282
(C1) H	0.237 and 0.249	(C1) H	0.309
O	-0.725	C	0.209
(O)H	0.521	N	-0.186

From the charge distribution it is possible to see that the CN group is truly electron withdrawing group and the OH group is electron donating. In the CN compound the values for the charges on the central nitrogen atom and the methyl groups are similar to those from the N(CH₃)₄⁺ molecule (see here). However the carbon adjacent to the CN group, has a less negative charge than the other carbons in the molecule, as the electrons are drawn to the cyanide group. However the OH group has a profound effect on the nitrogen centre as well as the adjacent carbon. It is an electron donating group so it can be seen that the nitrogen has a more negative charge than when it has no electron withdrawing or donating groups. The carbon adjacent to the OH group has a positive charge depsite the fact that OH is an electron donating group because of the electronegativity difference, making the easiest place to see the effect of the OH on the nitrogen atom.

Conclusions

In this project, the properties of onium cations were investigated using the B3LYP method and the 6-31(d,p) basis set. The molecules were successfully optimised and frequency analysis was used to confirm a minimum had been found. Additionally MO and NBO analysis was carried out on all molecules investigated.

The effect of changing the central ion was investigated and it was found that the charge distribution was significantly altered by altering the central atom. When phosphorus was the central atom, the positive charge was mostly centered on the central atom, as it is much more electropositive than the other 2 atoms investigates, whereas when nitrogen was the central atom it was slightly negatively charged despite having a formal positive charge, however usually it would be expected to hold much more of the negative charge due to its high electronegativity. When sulphur is the central atom, is has a positive charge, but less so that when phosphorus is the central atom, because sulphur has an intermediate electronegativity.

Secondly the effect of adding functional groups to one of the carbon atoms was investigated, using nitrogen as the central atom. The molecules produced had little symmetry due to the functional group breaking it, and causing a mistmatch in bond lengths and angles. Additionally adding a functional group changes the energies of the HOMO and LUMO. In the molecule where OH was added the LUMO was increased in energy in comparison to the unfunctionalised onium ion, and the molecule where CN was added the LUMO was lowered in energy. This means that N(CH₃)₃(CH₂)CN)⁺ is the best lewis acid of the 3, and the most able to accept electron, and N(CH₃)₃(CH₂)OH)⁺ is the worst lewis acid as it has the highest energy LUMO.