Thomas Arrow Inorganic Computational

Week 1

BH₃

3-21G Optimisation

BH₃ was optimised using the B3LYP method at the 321-g level. This resulted in the following log file: File:TA BH3 321G OPT.LOG. An extract of this shows the final forces on the molecule:

Item               Value     Threshold  Converged?
 Maximum Force            0.000220     0.000450     YES
 RMS     Force            0.000106     0.000300     YES
 Maximum Displacement     0.000940     0.001800     YES
 RMS     Displacement     0.000447     0.001200     YES
 Predicted change in Energy=-1.672478D-07

The details of this file are summarized in the table below:

File Name	TA_BH3_OPT
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	3-21G
Charge	0
Spin	Singlet
E(RB3LYP)	-26.46226429 a.u.
RMS Gradient Norm	0.00008851 a.u.
Dipole Moment	0.0003 Debye
Point Group	C_s

The bond lengths and angles are extracted from Gaussview and tabulated below.

B-H Bond Lengths (Å)	H-B-H Bond Angles (°)
1.19	120.0

631 Optimisation

The output from the previous calculation was used as the starting point for a further optimisation of the structure of BH₃. This was conducted with the B3LYP method at the 631-dp level. The output of this is attached in the following file: File:TA BH3 OPT 631DP.LOG

An extract of this shows convergence:

        Item               Value     Threshold  Converged?
 Maximum Force            0.000012     0.000450     YES
 RMS     Force            0.000008     0.000300     YES
 Maximum Displacement     0.000061     0.001800     YES
 RMS     Displacement     0.000038     0.001200     YES
 Predicted change in Energy=-1.069047D-09
 Optimization completed.
    -- Stationary point found.

The details of this file are summarised in the table below:

File Name	TA_BH3_OPT
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-26.61532360 a.u.
RMS Gradient Norm	0.00000707 a.u.
Dipole Moment	0.0001 Debye
Point Group	C_s

As before the bond lengths and angles are extracted from Gaussview and tabulated below.

B-H Bond Lengths (Å)	H-B-H Bond Angles (°)
1.19	120.0

GaBr₃ Optimisation

An optimisation of the structure of Gallium Bromide was performed on the Imperial College High Performance Computing Unit. The output of this is available on DSpace. The calculation was performed using the B3LYP method using the LANL2DZ basis set and pseudopotentials. Symmetry was constrained to D_3h. Proof of convergence is presented as an extract from the log file below:

        Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000003     0.001800     YES
 RMS     Displacement     0.000002     0.001200     YES
 Predicted change in Energy=-1.282682D-12
 Optimization completed.
    -- Stationary point found.

Details of the calculation are tabulated below:

File Name	TA_GaBr3_OPT_PP
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Charge	0
Spin	Singlet
E(RB3LYP)	-41.70082783 a.u.
RMS Gradient Norm	0.00000016 a.u.
Dipole Moment	0.0000 Debye
Point Group	D_3h

The bond lengths and angles are again tabulated below.

B-H Bond Lengths (Å)	H-B-H Bond Angles (°)
2.35	120.0

Obviously all lengths and angles are equal because of the constrained symmetry.

BBr₃ Optimisation

An optimisation of boron tribromide was also conducted however in this case a mixture of full basis set and pseudopotentials were used on the boron and bromine atoms respectively. The output of this is available at DSpace.

As before the item table is displayed below:

   Item               Value     Threshold  Converged?
 Maximum Force            0.000018     0.000450     YES
 RMS     Force            0.000010     0.000300     YES
 Maximum Displacement     0.000112     0.001800     YES
 RMS     Displacement     0.000064     0.001200     YES
 Predicted change in Energy=-2.260115D-09
 Optimization completed.
    -- Stationary point found.

Also the summary table of the calculation:

File Name	TA_BBr3_OPT_mixed
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	Gen
Charge	0
Spin	Singlet
E(RB3LYP)	-64.43644911 a.u.
RMS Gradient Norm	0.00000968 a.u.
Dipole Moment	0.0004 Debye
Point Group	C_s

B-H Bond Lengths (Å)	H-B-H Bond Angles (°)
1.93	120.0

Comparison of the Structures of BH₃, BBr₃ and GaBr₃

Molecule	M-X Bond length (M=B or Ga X=H or Br) (Å)
BH₃	1.19
BBr₃	1.93
GaBr₃	2.35

It is obvious that the bond length increases upon changing from H as a ligand to Br as a ligand. This is because the orbitals of bromine are more diffuse and thus induce a greater bond length.

Moving down the 3rd group from boron to gallium also induces an increase in bond length because of the larger an more diffuse orbitals of gallium compared to boron. It is also possible that less stabilisation of the empty p orbital by donation from the bromine into it is possible also resulting in a longer bond length.

Frequency Analysis of BH₃

A frequency analysis of the previously optimised BH₃ was conducted again at the 6-31 dp level using the B3LYP method.

This resulted in the Low Frequencies tabulated below:

 Low frequencies ---   -5.0068   -1.2203   -0.0053    0.9880    9.0091    9.0914
 Low frequencies --- 1162.9783 1213.1705 1213.1732

The 'real' non-zero frequencies are tabulated below.

No.	Description of Vibration	Wavenumber (cm^-1)	Intensity	Symmetry Label of D_3h point group
1	In and out of plane flexing of all hydrogen atoms	1163	14	A₂"
2	Scissoring of two hydrogen atoms	1213	14	E'
3	Two hydrogen atoms rocking in phase and one rocking anti phase in the the plane of the molecule	1163	14	E'
4	All the hydrogen atoms stretch in the plane in phase.	2582	0	A₁'
5	Two hydrogen atoms stretch asymmetrically while the third remains stationary.	2716	126	E'
6	All hydrogen atoms stretch in the plane; two in phase and one anti phase.	2716	126	E'

This results in an IR spectrum like that shown below.

This only shows three peaks because two pairs of vibrations are degenerate in energy while the sixth mode is not IR active.

Frequency Analysis of GaBr₃

A frequency analysis of GaBr₃ was undertaken using the previous optimisation. The full calculation is available on DSpace. The low frequencies line is pasted below to confirm convergence to a minimum.

Low frequencies ---   -0.5252   -0.5247   -0.0024   -0.0010    0.0235    1.2011
 Low frequencies ---   76.3744   76.3753   99.6982

The vibrations are analysed below:

No.	Description of Vibration	Wavenumber (cm^-1)	Intensity	Symmetry Label of D_3h point group
1	Bromine atoms rocking	76	3	E'
2	In plane scissoring of two bromine atoms.	76	3	E'
3	Symmetric out of plane bending of all three bromine atoms.	100	9	A₂"
4	Symmetric stretch. All bromine atoms stretch in phase in the plane.	197	4	A₁'
5	Anti phase stretching of two bromine atoms while the third remains stationary	316	57	E'
6	Two in phase and one antiphase bromine atoms stretch in plane.	316	57	E'

The IR spectrum is shown below:

Comparison Table of Vibrations

BH₃ Vibrational Mode	Equivalent GaBr₃ Vibrational Mode
1 - 1163cm^-1	3 - 100cm^-1
2 -1213cm^-1	1 - 76cm^-1
3 - 1163cm^-1	2 - 76cm^-1
4 - 2582cm^-1	4 - 197cm^-1
5 - 2716cm^-1	5 - 316cm^-1
6 - 2716cm^-1	6 - 316cm^-1

We can see that as expected all the vibrational modes for the gallium compound are lower in energy than the boron compound because for both increased reduced masses and increased force constants. The order remains basically the same except the out of plane bend in gallium lies higher out of order with comparison to the boron compound. This is because of an increased force constant. The two different sets of energies; each containing three modes exist because of the fact that the bending modes are less energetic than stretching. The purpose of carrying out a frequency analysis is two fold. To both determine the vibrational modes but also to check there are no imaginary frequencies which would symbolise an energy maxima not minima. The low frequencies should be zero. They represent the motions of the center of masses of the molecule. They only exist because of imperfections the frequency calculation. They are the '-6' in the 3N-6 vibrational modes we expect for a molecule.

Frequency Analysis of BBr₃ (This was done accidentally in place of GaBr₃)

A frequency analysis of previously optimised BBr₃ was conducted using a combination of a full basis set and pesudo potentials. The full calculation is available online at DSpace The low frequencies line is shown below.

Low frequencies ---   -4.7267   -0.0002   -0.0002   -0.0002    2.1216    3.4106
 Low frequencies ---  155.8879  155.9445  267.7003

Similarly to the previous molecule the vibrations are analysed in detail below.

No.	Description of Vibration	Wavenumber (cm^-1)	Intensity	Symmetry Label of D_3h point group
1	In plane scissoring of two bromine atoms.	156	0	E'
2	Rocking of one bromine atom	156	0	E'
3	Symmetric stretch. All bromine atoms stretch in phase in the plane.	267	0	A₁'
4	Symmetric out of plane bending of all three bromine atoms.	377	4	A₂"
5	Anti phase stretching of two bromine atoms while the third remains stationary	763	320	E'
6	Two in phase and one antiphase bromine atoms stretch in plane.	769	320	E'

The IR spectrum of this is shown below.

Although of the same point group, and therefore having the same vibrational modes as BH₃ it has a very different looking spectrum. For a start many modes that are IR active have no intensity because they result in so little change in dipole moment. This is because bromine is so much heavier than boron that they barely move relative to it. Indeed in this case you could view it as though it were the boron moving.

Comparison Table of Vibrations

BH₃ Vibrational Mode	Equivalent BBr₃ Vibrational Mode
1 - 1163cm^-1	4 - 337cm^-1
2 -1213cm^-1	1 - 156cm^-1
3 - 1163cm^-1	2 - 156cm^-1
4 - 2582cm^-1	3 - 267cm^-1
5 - 2716cm^-1	5 - 763cm^-1
6 - 2716cm^-1	6 - 769cm^-1

We can see that the vibrational modes are all lower in energy for BBr₃ than BH₃. This is because of the increased reduced mass of the molecule. The difference in ordering is that the out of plane bend is the lowest energy mode in BH₃ but has risen to the 4th in BBr₃.

Molecular Orbitals and NBOs

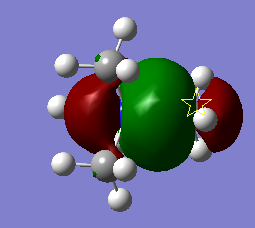
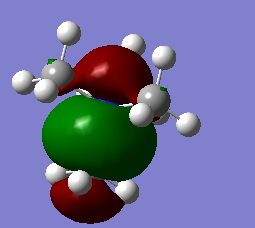
The full population molecular orbitals of BH₃ were found using gaussian. Some of these are shown below on an MO diagram of BH₃. The was created with the aid of lecture handouts.^[1] The output of this calculation is available on DSpace

From this we can see that the qualitative MOs are actually very similar to the calculated MOs. This shows that for simple molecules it is a valuable idea that does not require any computational time and still gives a good idea of the shape, and indeed energy ordering of the orbitals.

NBO analysis of NH₃

An NBO analysis of NH₃ was undertaken after previously optimizing at the 6-31G-d,p level. The results of this optimization and proof of convergence to a minima are shown below. The log files is available here: File:TA NH3 OPT.LOG and File:TA NH3 FREQ.LOG

 Item               Value     Threshold  Converged?
 Maximum Force            0.000005     0.000450     YES
 RMS     Force            0.000003     0.000300     YES
 Maximum Displacement     0.000010     0.001800     YES
 RMS     Displacement     0.000007     0.001200     YES
 Predicted change in Energy=-7.830248D-11
 Optimization completed.
    -- Stationary point found.

 Low frequencies ---  -11.6527  -11.6490   -0.0048    0.0333    0.1312   25.5724
 Low frequencies --- 1089.6616 1694.1736 1694.1736

	Optimisation	Frequency
File Name	TA_NH3_OPT	TA_NH3_FREQ
File Type	.log	.log
Calculation Type	FOPT	FREQ
Calculation Method	RB3LYP	RB3LYP
Basis Set	6-31G(d,p)	6-31G(d,p)
Charge	0	0
Spin	Singlet	singlet
E(RB3LYP)	-56.55776863 a.u.	-56.55776856 a.u.
RMS Gradient Norm	0.00000289 a.u.	0.00000279 a.u.
Dipole Moment	1.85 Debye	1.85 Debye
Point Group	C_3v	C_3v

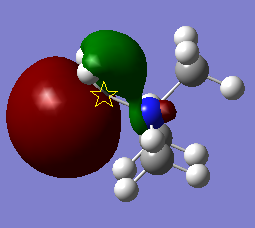
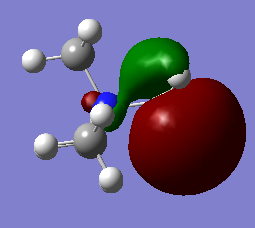
This structure was then subjected to a full population and NBO analysis enabling the NBO charge distribution across the atoms to be determined. The output of this calculation is available here File:TA NH3 MO.LOG. There are shown in the two pictures below both numerically and graphically. Where green is +1.125 and red is -1.125.

Energies of Reaction

We can also calculate energies of reaction but it is vital that all reactants and products are calculated with the same basis set. Otherwise the energies are in no way comparable. In the expected way we simply subtract the energies of the reactants from the energies of the products to finds the reaction energy. Obviously the equation must be balanced with the total number of each type of atom the same on either side. As an example here was have calculated the energy of the NH₃ BH₃ adduct. Proof that this optimisation was successful and converged is given below. The full content of the calculation is available on DSpace

Item               Value     Threshold  Converged?
 Maximum Force            0.000126     0.000450     YES
 RMS     Force            0.000058     0.000300     YES
 Maximum Displacement     0.000629     0.001800     YES
 RMS     Displacement     0.000375     0.001200     YES
 Predicted change in Energy=-1.770014D-07
 Optimization completed.
    -- Stationary point found.

Low frequencies ---   -0.0014   -0.0006    0.0006   15.3401   21.1049   29.6534
 Low frequencies ---  264.6397  632.2948  639.0223

File Name	log_89562
File Type	.log
Calculation Type	OPT+FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-83.22468861 a.u.
RMS Gradient Norm	0.00006056 a.u.
Dipole Moment	5.57 Debye
Point Group	C₁

The energy is calculated here: -83.22 a.u.-[-56.55 a.u. + -26.61 a.u.]=-0.05 a.u.

This can then be expressed in kJmol^-1 as: -135kJmol^-1

This is on the right scale of a bond energy and is a perfectly reasonable value.

Week 2 - Mini Project

Introduction

Ionic liquids are ionic salts that are molten at room temperature. They posess a number of useful properties that may make them well suited to future industrial applications. Of particular utility is that since they are dependent on the structure of the ions; and these can be customised and tweaked; we have the possibility of a bespoke solvent system.^[2] The aim of this experiment is to analyse the structures and symmetries of a variety of cations that may be of use in ionic solvent systems. We shall be considering in this project three different methyl substituted hetero atoms for use as cations. They are shown below. Specifically [N(CH₃)₄]⁺ [P(CH₃)₄]⁺ and [S(CH₃)₃]⁺. Furthermore we shall also consider the impact of substituting electron donating and withdrawing groups onto the methyl groups; these are also shown below.

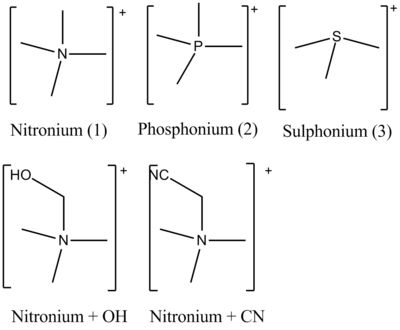
Structures of Cations

The structure of all three cations was optimized with the B3LYP method at the 6-31G-(d,p) level and the frequencies were calculated in order to shown convergence to a minima. The summary for these calculations is presented below; along with the proofs of convergence and the low frequencies lines.

	1	2	3
File Name	log_89584	log_89564 (2)	log_89565
File Type	.log	.log	.log
Calculation Type	OPT + FREQ	OPT + FREQ	OPT + FREQ
Calculation Method	RB3LYP	RB3LYP	RB3LYP
Basis Set	6-31G(d,p)	6-31G(d,p)	6-31G(d,p)
Charge	1	1	1
Spin	Singlet	Singlet	Singlet
E(RB3LYP)	-214.18127933 a.u.	-500.82701719 a.u.	-517.68326471 a.u.
RMS Gradient Norm	0.00005147 a.u.	0.00005003 a.u.	0.00005624 a.u.
Dipole Moment	0 Debye	0 Debye	0.97 Debye
Point Group	C₁	C₁
Item table	Item Value Threshold Converged? Maximum Force 0.000143 0.000450 YES RMS Force 0.000044 0.000300 YES Maximum Displacement 0.001110 0.001800 YES RMS Displacement 0.000306 0.001200 YES Predicted change in Energy=-3.321860D-06 Optimization completed. -- Stationary point found.	Item Value Threshold Converged? Maximum Force 0.000196 0.000450 YES RMS Force 0.000045 0.000300 YES Maximum Displacement 0.001293 0.001800 YES RMS Displacement 0.000317 0.001200 YES Predicted change in Energy=-4.023652D-07 Optimization completed. -- Stationary point found.	Item Value Threshold Converged? Maximum Force 0.000160 0.000450 YES RMS Force 0.000042 0.000300 YES Maximum Displacement 0.001394 0.001800 YES RMS Displacement 0.000343 0.001200 YES Predicted change in Energy=-9.648087D-08 Optimization completed. -- Stationary point found.
Low Frequencies	Low frequencies --- -9.5034 -0.0012 -0.0009 0.0003 5.4827 14.9223 Low frequencies --- 190.3339 288.6950 292.0315	Low frequencies --- -32.4246 -0.0018 0.0016 0.0021 14.9221 30.5928 Low frequencies --- 154.6517 183.6753 191.7797	Low frequencies --- -27.7555 -8.7909 -0.0041 -0.0040 -0.0017 11.5172 Low frequencies --- 158.6701 193.9140 200.1504
DSpace Link	Link	Link	Link

From these optimised structures the bond lengths and angles can be determined in gaussview.

Bond Lengths

The C-X bond lengths (where X=N, P or S) for each of the different cations are tabulated below.

X	Bond Lengths (Å)
N	1.51
P	1.82
S	1.82

As you can see the nitronium bond length is much shorter than the phosphonium or the sulphonium bond length. This is exactly as expected because as we move down the periodic table to larger atoms with more diffuse orbitals bond lengths generally increase.

Also interesting to note is the fact that the phosphonium and sulphonium ions have the same bond length. This is slightly surprising because they have the same number of electron pair surruoinding them which would suggest a tighter set of orbitals on the element with the higher atomic number (S) however this effect is obviously offset by the replacement of a methyl group with a lone pair.

Bond Angles

Also of interest is the C-X-C angle (where X=N, P or S). These are tabulated below.

X	Bond Angles (°)
N	109.5
P	109.5
S	102.8

Clearly here we see that as might be expected the perfectly tetrahedral nitronium and phosphonium. We also see the the angle in the sulphonium has been distorted. Again as one would expect from simply considering VSEPR(valance shell electron pair repulsion). This states that the lone pair of electrons is more repulsive to other pairs than a bonding pair. This can be rationalised by thinking of it being held closer to the central ion because there is nothing to pull electron density away.

MOs of Nitronium

In the table below a number of different MOs for the nitronium ion are reproduced and their characteristics analysed in order to get a sense of the molecular orbital structure.

No.	Energy (Hartrees)	Description
6	-0.90699	This MO is a relatively highly bonding MO. The majority of the electron density lies along the C-N bond. There are nodal planes which lie on the highlighted C and nitrogen atoms and normal to their bond. The MO is relatively localised to the highlighted carbon and nitrogen atom. However you can just the that there is also a small amount of electron density associated with the other carbon atoms.
9	-0.90685	This is an almost identical MO to that of 6. Correspondingly it also has a very similar energy however, due to lack of symmetry in the molecule the calculation has rendered it non-degenerate to six. It has the same nodes and localisations.
10	-0.71144	This MO has no nodal planes but does have nodal surfaces. By definition there are obviously nodes at each atom but in particular we see a change of sign of the wave function as it passes through the central nitrogen. This orbital is relatively anti-bonding with the bulk of the electron density lying beyond the carbon atom highlighted. Compared to the previous two orbitals it is more localised to the nitrogen and highlighted carbon.
16	-0.71142	Similar to 10 but obviously slightly perturbed by asymmetry in the calculation. Same nodes, antibonding character and localisation.
21	-0.71135	Also similar to 10 but obviously slightly perturbed by asymmetry in the calculation. Same nodes, antibonding character and localisation.

NBO Analysis of Cations

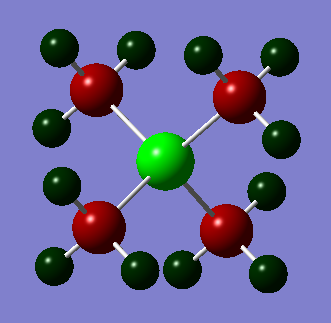
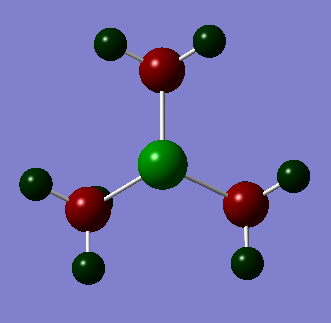
Also conducted is an NBO analysis of the charge distribution. This is depicted below where atoms are colored by charge. Bright green is 2 and bright red is -2.

Nitronium

Phosphonium

Sulphonium

Atom	NBO Charge
N	-0.295
C	-0.483
H	0.269

Atom	NBO Charge
P	1.667
C	-1.060
H	0.289

Atom	NBO Charge
S	0.917
C	-0.845
H	0.297

From these three pictures it is easy to see that varying the central atom heavily impacts the location of the charge. For example in nitronium we can see that is it relatively evenly spread out all be it was all the positive charge on the hydrogen atoms and both the carbon and nitrogen atoms negative. We can also see that despite nitrogen being the more electronegative element the carbon atoms are each more negatively charged; even though there are four of them. We can also see that the phosphonium ion has the greatest positive charge density on the phosphorus atom. One would expect this to make it less strongly bound to an anion because the positive charge is shielded by negative charge on the carbons than the nitronium. We can see that this situation is similar in the sulphonium but less pronounced. This is probably due to the presence on the lone pair on the sulphur.

Other information that we can extract from the NBO analysis is discussed below for each molecule in turn.

Nitronium

We see that each of the C-N bonds are contributed 65%:35% by the nitrogen and carbon respectively. We also see that the bonding from the nitrogen is 25% s character and 75% p character whereas the carbon contributed 20% s character and 80% p character. Nitrogen shows a perfect sp³ mix because it is in a tetrahedral environment whereas the carbon is slightly distorted and also has better s overlap with the hydrogen atoms (probably due to closeness in energy level) that give it slightly more p bonding character. There is nothing of note in 2nd order perturbations.

Phosphonium

Similarly we see a 65%:35% split in P-C bond contributions respectively. P contributes 25% s character and 75% p whereas carbon now contributes far more s character at 35% to 65% p. This is probably because an increase in bond length means less directionality in the bonding. There is nothing of note in 2nd order perturbations.

Sulphonium

In this we see approximately equal contributions to the sulphur carbon bond and for both atoms this is ca. 20% s and 80% p. This may be due to the impact on the lone pair on sulphur. We can see in the 2nd order perturbation that the lone pair is partially mixing with C-H bonds to reduce their energy by 2.3kcalmol^-1

Effect of functionalising the methyl groups

We will now consider the effects of placing an electron withdrawing or donating group on one of the methyl groups of the nitronium ion. This was done by adding a single OH or CN group. The details of the calculations for this and proof of convergence are shown below:

CN

OH

File Name	logfile (1)
File Type	.log
Calculation Type	OPT+FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	1
Spin	Singlet
E(RB3LYP)	-306.39377061 a.u.
RMS Gradient Norm	0.00000306 a.u.
Dipole Moment	5.56 Debye
Point Group	C₁

File Name	log_89618
File Type	.log
Calculation Type	OPT+FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	1
Spin	Singlet
E(RB3LYP)	-289.39471484 a.u.
RMS Gradient Norm	0.00000620 a.u.
Dipole Moment	2.14 Debye
Point Group	C₁

         Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000015     YES
 RMS     Force            0.000001     0.000010     YES
 Maximum Displacement     0.000050     0.000060     YES
 RMS     Displacement     0.000018     0.000040     YES
 Predicted change in Energy=-1.031025D-10
 Optimization completed.
    -- Stationary point found.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000013     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.001109     0.001800     YES
 RMS     Displacement     0.000290     0.001200     YES
 Predicted change in Energy=-1.681451D-08
 Optimization completed.
    -- Stationary point found.

 Low frequencies ---   -7.4599    0.0005    0.0008    0.0010    6.0683   17.1612
 Low frequencies ---   92.0165  154.5874  212.8251

 Low frequencies ---  -11.8806    0.0005    0.0006    0.0008    8.2921   14.9127
 Low frequencies ---  134.2245  214.4008  255.8744

DSpace

NBO Analysis

In the graphical depiction below bright red corresponds to -0.75 and bright green to +0.75.

Nitronium

Nitronium and CN

Nitronium and OH

Atom	NBO Charge
N	-0.295
C	-0.483
H	0.269

Atom	NBO Charge
N (central)	-0.289
C without substitution	-0.485 - -0.488
C with substitution	-0.358
C of nitrile	0.289
N of nitrile	-0.186
H on unsubstituted carbon	0.269 - 0.282
H on substituted carbon	0.389

Atom	NBO Charge
N	-0.322
C without substitution	-0.491 - -0.494
C with substitution	-0.088
H without substitition	0.262-0.282
H with substitution	0.237-0.249
H of hydroxyl	0.512
O	-0.725

The effects are clear and as expected. The electron withdrawing group reduces the negative charge on the central nitrogen whereas the OH group increases it. The protons lose their symmetry of charge distribution but in general become more positively charged in both cases. Also, as one would expect the substituted carbon is far more greatly perturbed than those that remain the same.

MO Analysis

The HOMOs and LUMOs for this triad of molecules and their energies in hartrees are tabulated below.

	Nitronium	Nitronium + CN	Nitronium + OH
LUMO	-0.06150	-0.07052	-0.12458
HOMO	-0.71135	-0.50923	-0.48764

The main difference in the LUMOs is that in the pure nitronium and the OH substituted variant the LUMO is still delocalised over the majority of the molecule. It is not particularly susceptible to nucleophilic attack. In contrast to this the CN substituted molecule has the LUMO focused on the cyano group providing an easy area for attack. Obviously this makes it less suitable for use as a solvent because it may well react with the solute.

In terms of the HOMOs the main difference is that while the cyano substituted molecule and pure nitronium are spread over the majority of the molecule the OH HOMO is basically just the oxygen lone pair. This makes it susceptible to nucleophilic attack. It also means that it may well be able to participate in hydrogen bonding which may or may not be a good thing. If it increases the boiling point this may allow it to be used as a solvent at higher temperature however it may also raise the melting point in which case it may no longer be a liquid at useful temperatures.

It seems in both cases that substitution has lowered the energy of the LUMO and raised the energy of the HOMO. This means that it is more likely to be able to undergo some form of reaction.

Conclusion

It is very possible to model the ions of ionic liquids using computational quantum mechanics. It allows us to predict their possible chemical reactions and consider things like charge density. However, it is suggested that molecular dynamics modelling should also be undertaken in order to find out very important facts like melting and boiling point of them.

References

↑ Imperial College Chemistry 2nd Year - Molecular Orbitals Course Notes
↑ Ionic Liquids--Solvents of the Future? Robin D. Rogers and Kenneth R. Seddon Science 31 October 2003: 302 (5646), 792-793. [DOI:10.1126/science.1090313]

[1] Imperial College Chemistry 2nd Year - Molecular Orbitals Course Notes

[2] Ionic Liquids--Solvents of the Future? Robin D. Rogers and Kenneth R. Seddon Science 31 October 2003: 302 (5646), 792-793. [DOI:10.1126/science.1090313]

[1]

[2]

Thomas Arrow Inorganic Computational

Week 1

BH3

3-21G Optimisation

631 Optimisation

GaBr3 Optimisation

BBr3 Optimisation

Comparison of the Structures of BH3, BBr3 and GaBr3

Frequency Analysis of BH3

Frequency Analysis of GaBr3

Comparison Table of Vibrations

Frequency Analysis of BBr3 (This was done accidentally in place of GaBr3)

Comparison Table of Vibrations

Molecular Orbitals and NBOs

NBO analysis of NH3

Energies of Reaction

Week 2 - Mini Project

Introduction

Structures of Cations

Bond Lengths

Bond Angles

MOs of Nitronium

NBO Analysis of Cations

Nitronium

Phosphonium

Sulphonium

Effect of functionalising the methyl groups

NBO Analysis

MO Analysis

Conclusion

References

BH₃

GaBr₃ Optimisation

BBr₃ Optimisation

Comparison of the Structures of BH₃, BBr₃ and GaBr₃

Frequency Analysis of BH₃

Frequency Analysis of GaBr₃

Frequency Analysis of BBr₃ (This was done accidentally in place of GaBr₃)

NBO analysis of NH₃