Rep:Mod:LEH1234
1st Year Molecular Modelling 2 Lab - Lucy Haggerty
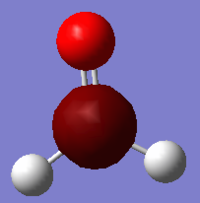
Ammonia, NH3
Molecule: Ammonia, NH3
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy: -56.55776873 a.u.
RMS gradient: 0.00000485 a.u.
Point group: C3V
Optimised N-H bond distance: 1.01798 Å
Optimised H-N-H bond angle: 105.741o
Charge on N: -1.125
Charge on H: 0.375
It is expected that the N in this molecule will have a negative charge as it has a higher electronegativity so a higher electron density. H is less electronegative than N so will have a positive charge.
Stanton et al reported a N-H bond length range to be between 1.03-1.05 Å. [1] The optimised bond length lies only slightly outside of this range suggesting that Gaussian can accurately calculate bond lengths during optimisation.
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986275D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
NH3 |
Vibrations
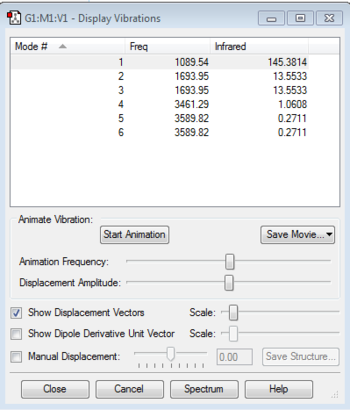
There are 4 atoms in total so by using the 3N-6 rule, it is expected that there should be 6 modes of vibration. From the table, it shows that modes 2 and 3 are degenerate as they have the same energies. This is also the case for modes 5 and 6. Modes 1, 2 and 3 are "bending" vibrations and modes 4, 5 and 6 are "bond stretch" vibrations. Vibration mode 4 is highly symmetric and mode 1 is known as the "umbrella" mode due to its unique bending motion. In an experimental spectrum of gaseous ammonia, you would expect to see four bands due to the 2 pairs of degenerate modes.
Hydrogen, H2
Molecule: Hydrogen, H2
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy: -1.17853936 a.u.
RMS gradient: 0.00000017 a.u.
Point group: D∞H
Optimised H-H bond distance: 0.74279 Å
One frequency recorded as 4465.68. No negative frequencies so optimisation must be complete.
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
H2 |
Nitrogen, N2
Molecule: Nitrogen, N2
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy: -109.52412868 a.u.
RMS gradient: 0.00000060 a.u.
Point group: D∞H
Optimised N-N bond distance: 1.10550 Å
One frequency recorded as 2457.33. No negative frequencies so optimisation must be complete.
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401020D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
N2 |
The Haber-Bosch Process Calculation
N2 + 3H2 -> 2NH3
E(NH3)= -56.55776873 a.u.
2*E(NH3)= -113.1155375 a.u.
E(N2)= -109.52412868 a.u.
E(H2)= -1.17853936 a.u.
3*E(H2)= -3.53561808 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579074 a.u.
ΔE = -146.48 kJ/mol (2 d.p)
The ammonia product has a more negative energy so is more stable than its gaseous reactants. This is shown from a negative ΔE meaning it is an exothermic reaction so the products formed have increased stability.
Bicer et al reported a value of -46.22 kJ/mol for the formation of ammonia in the Haber-Bosch process.[2] This value differs greatly from the calculated energy from these optimised structures. This could be due to the inaccuracies in the approximations made on Gaussian during the calculations. Using the calculation method B3LYP approximates by solving the Schrodinger equation. Instead of a simple classical mechanic problem when calculating vibrations, Gaussian now has a quantum problem. An experimental value will differ from a computational calculation due to the different systems and conditions. In a laboratory, conditions are manipulated however in Gaussian the molecule is in a vacuum so will have a very different energy to its true value.
Formaldehyde, H2CO
Molecule: Formaldehyde (methanal) H2CO
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy: -114.50319933 a.u.
RMS gradient: 0.00006910 a.u.
Point group: C2V
Optimised C=O bond distance: 1.20676 Å
Optimised C-H bond distance: 1.11056 Å
Optimised O=C-H bond angle: 122.390 o
Charge on O: -0.494
Charge on H: 0.221
Charge on C: 0.137
A negative charge is expected on the oxygen atom as it has a high electronegativity so will withdraw electrons from the carbon. Therefore, this means that the carbon and oxygen atoms have a positive charge.
H2CO |
Item Value Threshold Converged?
Maximum Force 0.000182 0.000450 YES
RMS Force 0.000080 0.000300 YES
Maximum Displacement 0.000231 0.001800 YES
RMS Displacement 0.000142 0.001200 YES
Predicted change in Energy=-3.380743D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1106 -DE/DX = -0.0001 !
! R2 R(1,3) 1.1106 -DE/DX = -0.0001 !
! R3 R(1,4) 1.2068 -DE/DX = -0.0002 !
! A1 A(2,1,3) 115.2203 -DE/DX = 0.0 !
! A2 A(2,1,4) 122.3899 -DE/DX = 0.0 !
! A3 A(3,1,4) 122.3899 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Vibrations
Vibration |
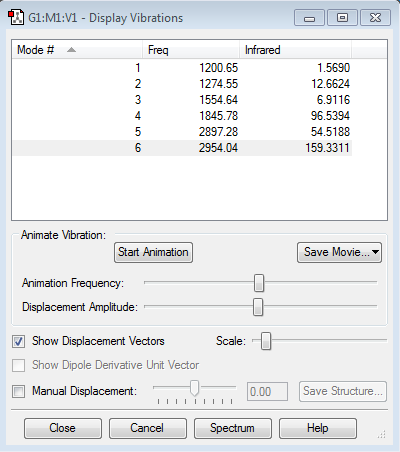
There are a total of 6 vibrations found which fits the 3N-6 rule. There are no degenerate vibrations as all frequencies are the same. Vibration modes 1, 2 and 3 are bending vibrations and modes 5 and 6 are bond stretching vibrations. Mode 4 appears to be both bending and stretching, with the C-H bonds bending and the C=O bond stretching. This is shown above. In an experimental spectrum of gaseous formaldehyde, you would expect to see 6 distinct bands. The IR spectrum of this optimised structure is shown below.
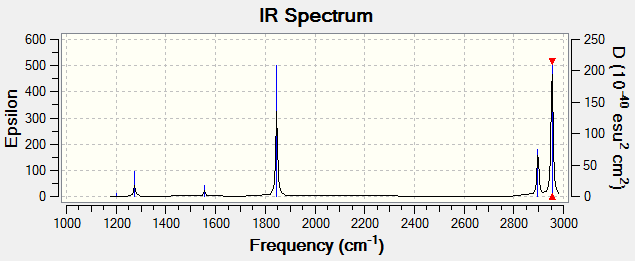
These recorded vibrational frequencies can be compared to literature values where formaldehyde synthesised in the laboratory is analysed by IR spectroscopy. Blau et al reported 6 fundamental vibrational bands. The values of these frequencies in cm-1 are as follows: 1746.0, 1500.6, 2843.4, 1247.3, 1163.3 and 3003.3.[3] These values are similar to the vibrational frequencies calculated by Gaussian, shown in the picture above. This suggests that the software accurately calculates these vibrational modes so the IR spectrums generated are reliable. Gaussian is capable of doing this as the calculation only requires a mass and bond length so vibrations can be easily generated using simple classical mechanics.
Molecular Orbitals
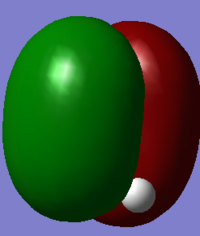
The first two molecular orbitals to be found are incredibly deep in energy and both occupied with 2 electrons each. The AO's that contribute to these are the 1s orbitals from the C and O. These orbitals contain core electrons so are held very close to the nucleus. This means there is little overlap between these AO's once the MO has formed. The two images above show these two MO's - the first shows the bonding orbital between the two 1s orbitals which would increase bond strength. Its energy was recorded to be -19.17003 a.u. The second image shows the antibonding orbital which would decrease bond strength. Its energy was recorded to be slightly higher at -10.28952 a.u.
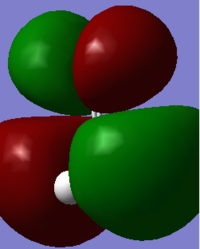
At a higher energy level -0.39919 a.u. , the MO shown above is found. The AO's that contribute to this is the p orbital of the C and O in the z direction. These two AO's overlap due to their matching phases and form a bonding pi orbital which is occupied with two electrons. This would further strengthen the bond.

The MO found at the next level has an energy of -0.26816 a.u. and is shown above. This MO is the highest occupied molecular orbital (HOMO) of formaldehyde, containing two electrons. The AO's that make up this are the p orbitals of C and O. They have a different orientation to the AO's in the previous bonding MO. They also have opposite phases so form an antibonding orbital - this will decrease the bond strength.
The first unoccupied MO is shown in the image above which has a reported energy of -0.04309. The MO can be considered to be the LUMO of formaldehyde. The AO's that contribute to this are the same p orbitals of C and O that form the bonding MO in MO 3. However they are now in opposite phase so an antibonding orbital has formed. Due to this orbital not being occupied, it does not have an affect on bond strength.
Formox Process Calculation
CH3OH + 1/2 O2 --> CH2O + H2O
The molecules, CH3OH, O2 and H20 were optimised using B3LYP method and 6-31G(d,p) basis to find the molecules final energies. The links to the log files of these optimisations are below. To ensure the optimisation had occurred successfully, the RMS gradients and vibrations were checked for suitable values. From these results the final energies can be used to calculate the enthalpy change of formation of formaldehyde in the Formox process.
File:LH1216 O2 OPTF POP.LOG File:LH1216 H2O OPTF POP.LOG File:LH1216 CH3OH OPT POP.LOG
E(O2)= -150.25742434 a.u.
1/2*E(O2)= -75.12871217 a.u.
E(CH3OH)= -115.72396421 a.u.
E(CH2O)= -114.50319933 a.u.
E(H2O)= -76.41973740 a.u.
ΔE=[E(CH2O)+ E(H2O)] - [(E(CH3OH)+ 1/2*E(O2))]= -0.07026035 a.u.
ΔE = -184.47 kJ/mol (2 d.p)
This value suggests that the products are more stable than the reactants so the reaction is exothermic, giving a negative ΔE.
Reuss et al reported a value of -159 kJ/mol.[4] The two values differ due to many reasons. The systems that the calculation takes part in and the conditions used in this reaction has to be taken into consideration. Reuss et al carried out the oxidation of methanol at atmospheric pressure, a temperature between 600-720°C and with a silver catalyst. This system is completely different to the system used in Gaussian to calculate energies. The molecules created in Gaussian are within a vacuum so the approximated energy will be very different as they are experiencing very different conditions. If a solvent is used in the reaction then the solvent molecules can be added around the molecule on Gaussian - this will bring the calculated energies closer to the true value.
References
- ↑ J. F. Stanton and N. S. Kadagathur, J. Chem. Phys., 1995, 102, 1096
- ↑ Y. Bicer, I. Dincer, C. Zamfirescu, G. Vezina and F. Raso, J. Clean. Prod., 2016, 135, 1379–1395.
- ↑ H. H. Blau and H. H. Nielsen, J. Mol. Spectrosc., 1957, 1, 124–132
- ↑ G. Reuss, W. Disteldorf, A. O. Gamer and A. Hilt, Ulmann’s Encycl. iIndustrial Chem., 2012, 15, 735–768.