Rep:Mod:LBinfieldModule3

Module 3: Physical Chemistry

In this module computational chemistry was used to model transition states and determine their theoretical energies, starting with the Cope rearrangement

The Cope Rearrangement

The Cope rearrangement is a 3,3 sigmatropic shift (see right )

The Cope rearrangement

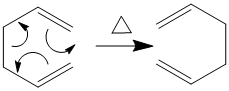
that has been extensively studied amongst much debate about its mechanism, although general concsensus has now been reached that the reaction proceeds via a concerted mechanism with either a 'chair'-like or 'boat' like shape. In order to find out which one is more likely, the reactant 1,5 hexedine must first be optimised, as must the two possible transition states to find out which one is the lowest energy.

the two possible transition states available in the Cope rearrangement

Optimisation of the hexadiene molecule

1,5 hexadiene can exist in either an anti- or gauche- conformation.

Anti/Gauche conformation

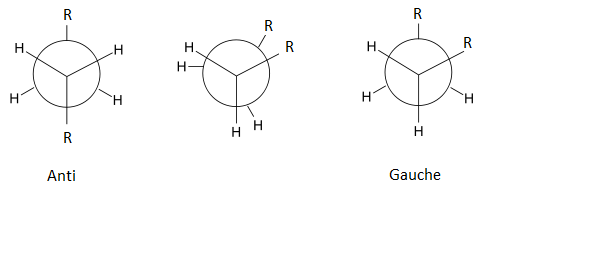
To find out which is the lowest energy, the ten different conformers of 1,5 hexadiene are shown below with their respective energies. After optimizing each molecule, I checked that the calculations has converged by viewing the text file of the calculation and ensuring that the following was present(example taken from the .log file of the Gauche-2 conformer:

Item               Value     Threshold  Converged?
 Maximum Force            0.000010     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000698     0.001800     YES
 RMS     Displacement     0.000230     0.001200     YES
 Predicted change in Energy=-5.253120D-09
 Optimization completed.
    -- Stationary point found.

HF/312G optimisation of the possible conformers of 1,5 hexadiene molecule

Name	Molecule	Energy(a.u)	Point group
Anti-1		-231.69260236	C2
anti-2		-231.69253527	C1
anti-3		-231.68907066	C2h
Anti-4		-231.69097054	C1
Gauche-1		-231.68771617	C2
Gauche-2		-231.69166702	C2
Gauche-3		-231.69266122	C1
Gauche-4		-231.69153036	C2
gauche-5		-231.68916017	C1
Gauche 6		-231.68916020	C1

Optimisation of the possible lowest energy conformers of 1,5 hexadiene using a 631G* basis set

Name	Molecule	Energy(a.u)	Point group
Anti-1		-234.61171032	C1
Anti-2		-234.61179055	C2
Gauche-2		-234.61070764	C2
Gauche-3		-232.98286013	C1

From this table it can be seen that anti-2 structure is the lowest energy conformer. This is agreement with theory which suggests that the lowest energy conformer will minimise steric and electronic repulsion between the H and R groups, as seem in smaller molecules such as ethane. The lowest energy is therefore -234.61179055 a.u which corresponds to a difference of only 0.2 KJMol^-1 when compared to the second lowest energy conformer, anti-1, although this is much more stable that what was calculated at the lower basis set to be the third least stable conformer, Gauche-2. This shows better how the molecule is arranged in space so that it is the most stable possible. The table below shows the bond length and bond angles of the lowest energy conformers compared with typical C-C and C=C values.

Conformer	C1=C2 bond length (Å)	C2-C3 Bond length(Å)	C3-C4 bond length(Å)
Anti-1	1.33349	1.50428	1.54808
Gauche-2	1.33306	1.590466	1.54827
Anti-2	1.33346	1.50411	1.54763
Typical values	1.353	1.543	1.543

Performing the same calculations with a better basis set in each of the above cases lowered the total energy significantly and changed the order in stability. Since these calculations involve quite small differences in energy, it is important to run the calculations using as high a basis set as possible. The bond angles calculated by Gaussian did not in general change when comparing the two, but the bond lengths changes quite significantly in some cases, reflecting in most cases the lower energies.

Screenshot of the anti-2 vibrations

Frequency Analysis and Thermochemistry

A frequency alalysis was run of the 4 optimised (631G*) molecules with the lowest energy. The sum of the electronic and zero-point energies is the total energy of the system at 0k, whereas the second column includes the energy at 298K. The thermal enthalpies include the contribution from RT and the last column contains an entropic term (G(p,T) = H − TS). I confirmed that all the vibrations were 'real' by ensuring that they were all positive and that the low frequencies were <15cm^-1 - for example, the following is from the .log file from the Gauche-2 -

Low frequencies ---   -7.0664   -2.1717   -0.0007    0.0004    0.0008   14.8363
 Low frequencies ---   69.0818  105.2441  111.4065

Molecule	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Sum of electronic and thermal enthalpies	Sum of electronic and thermal free energies
anti-1	-234.469298	-234.461966	-234.461022	-234.500862
anti-2	-234.466494	-234.461003	-234.460059	-234.495704
Gauche-2	-234.468205	-234.460939	-234.459995	-234.499097
Gauche-3	234.468693	-234.461464	-234.460520	-234.500105

Optimization of the 'boat' and 'chair' transition states

optimised 'Chair' transition state

Using the HF/321G basis set the transition state for both the 'chair' and the 'boat' structures' were optimised. Bond length using the frozen coordinate method is 2.02012Å after the molecule was optimized with the C-C bonds that will form in the Cope rearrangement fixed and then optimized again. To confirm that the optimized structures were in fact the ones found, the vibrations corresponding to the Cope rearrangements in each case are shown below.

'boat' transition structure	'Chair' transition structure

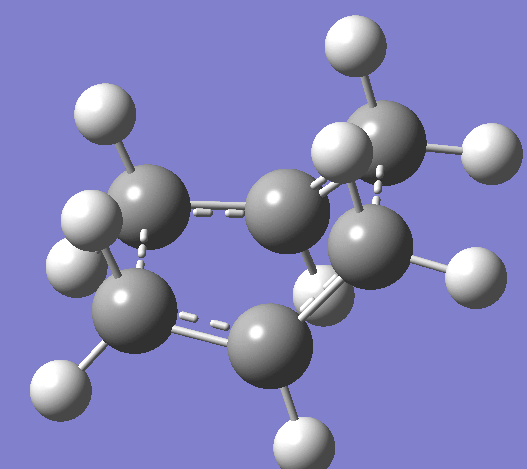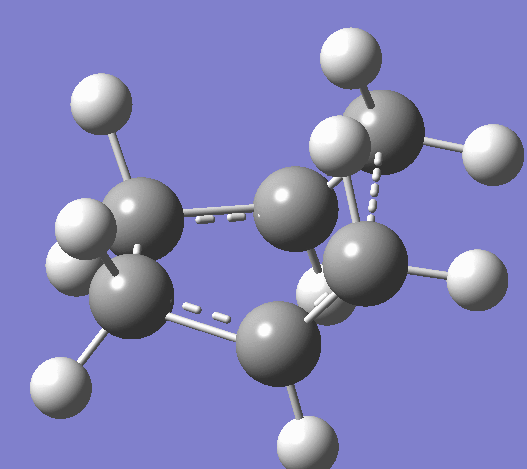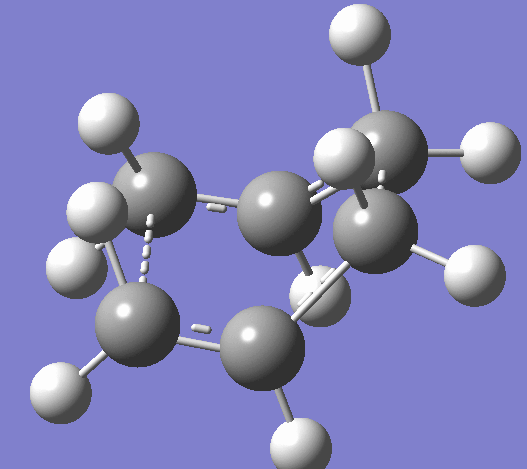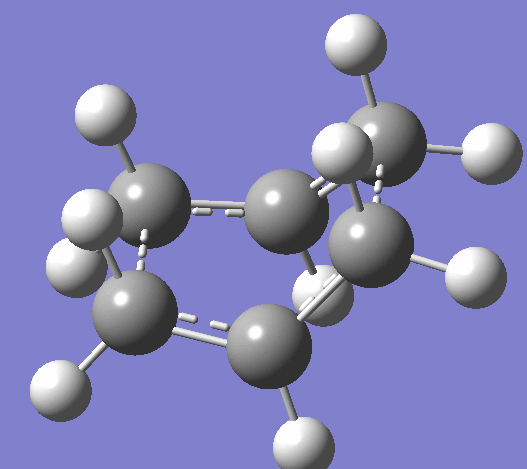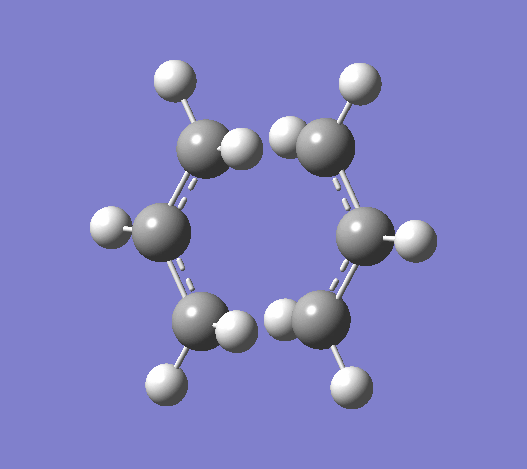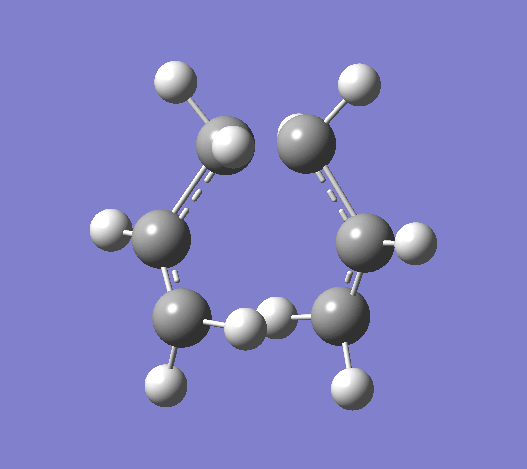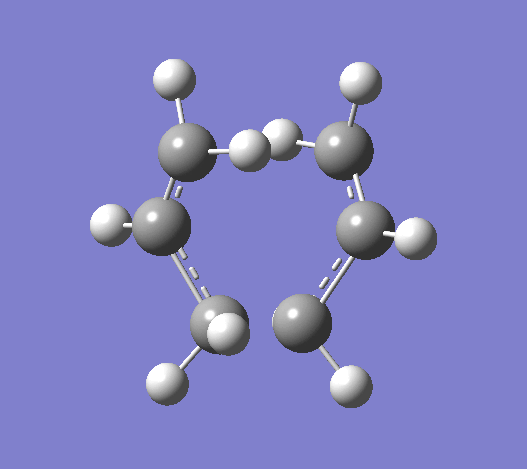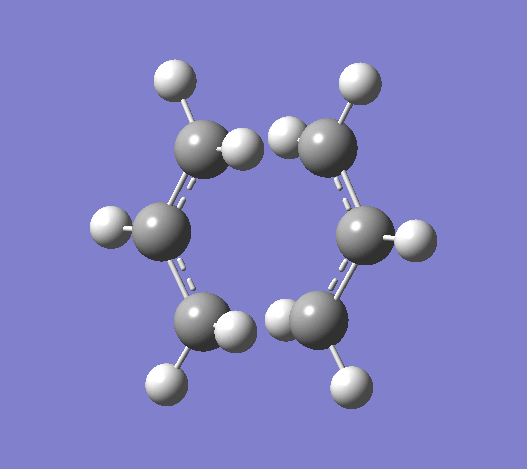Using the anti-2 optimised conformer (see above), The 'boat' transition state was also calculated. Using a QST2 method, Gaussian will not compute ethe correct transition state if the 'guess' TS is too far from the real minimum, so a calculation using the 'reactant' and 'product' shown below was run. The 'boat' transition state was also optimised using a frozon coordinate method, in which the bond that will eventually be formed in the reaction are fixed then those bonbds are minimised.

'product' structure

'reactant' structure

It is difficult to predict which conformers of 1,5 hexadiene corresponds to which transition state and leads to which product, So the following method was used to compute the specific intermediates.

Intrinsic Reaction Coordinate

An 'IRC' calculation was run to try and determine which 1,5 hexadiene conformer leads to which transition state mechanism. It was necessary to run the final result of ther the IRC calculation to a minumum which resulted in The following file which as can be seen from this Animation is closest in energy to a 'gauche-3' conformation in the table above. This means that the molecule will have to overcome another maximum to get into the gauche-3 conformer from it's most stable state, the 'anti-2' conformer.

Chair transition state- a minimum was not reached by perfoming an IRC claculation, so I ran an optimisation as if the last product that the intrinsic reaction coordinate reached was at minimum

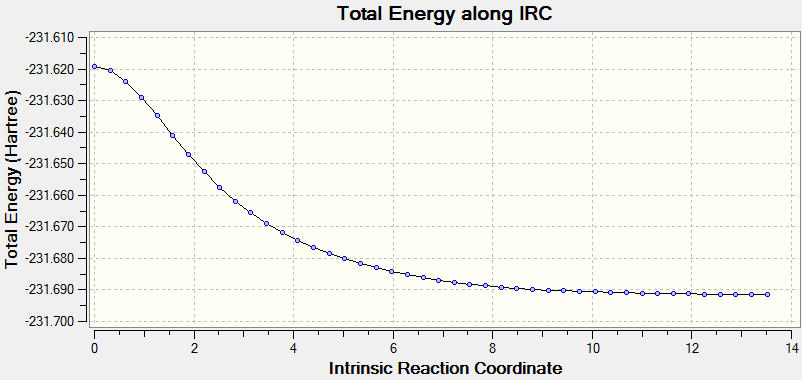
The same process was followed, this time with the 'boat' transition state which was found to be closest in energy to this structure . The Sum of Thermal and Free energies are -231.570640 a.u for the 'boat' and -231.570138 for the 'chair', making the precursor to the 'boat' transition state more stable by 0.000502a.u or 1.318001 KJmol_-1.

The IRC minimised structure for the 'boat' transition state

The IRC is a method which maps out the energy of the reaction by taking various points and measuring and mapping the energy at these points to produce a graph which should have a minimum.

Total reaction energies

To ascertain which transition state was the most stable and therefore the most likely to occur, the transition states were both optimised using the higher 631g* basis set and the energies of the boat and chair conformations were found to be -234.54309304a.u and -234.55446198a.u respectively, meaning the chair conformation appears to be more stable by 29KJmol^-1. The table below compares this information with literature values.

	Total energy using the 631/G basis set (hartree)	Sum of Electronic and Zero-point Energy (0K)	Sum of Electronic and Thermal Energy (298.15K)	Activation energy at 298K (hartree)	Activation energy at 298K (Kcal-1)	Activation energy at 0K (Kcal-1)	Experimental activation energy at 0K(Kcal-1)
anti-2 conformer	-234.6117906	-234.466494	-234.461003
Boat TS	-234.543093	-234.402339	-234.396005	0.064998	40.78689498	43.10843098	44.7 ± 2.0
Chair TS	-234.5544137	-234.411621	-234.40516	0.061334	38.48769834	36.00457952	33.5 ± 0.5

Experimental values are similar to the calculated values, although a higher basis set would have to be used to factor in more components and achieve a closer result.

From this table it can be clearly shown that the 'chair' transition state is easier for the reactant to reach than the 'boat', and therefore it is likely that the reaction will proceed via a 'chair'.

The Diels-Alder Reaction

In this exercise the transition state energies of the pericyclic reaction of maleic anhydride with cyclohexadiene were calculated and analysed. The HOMO and LUMO of the two species must interact with the same symmetry in order for the reaction to be favourable, and therefore the MO's of the two reactants, transition states and products were also analysed.

MOs of cis-butadiene

The HOMO and LUMO of cisbutadiene

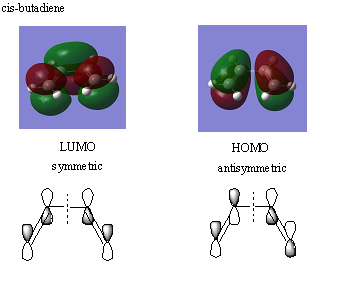
The data below comes from an optimisation of cis-butadiene, a diene which reacts with e,g ethene in the Diels-Alder Reaction. The bond lengths of the C=C double bonds was 1.35520Å whilst the C-C single bond was 1.5400Å.

Butadiene and Ethene

alt-the diels alder reaction

The transition state was optimised using the Frozen coordinate method. A vibration was found at -818.42cm^-1 which is shown below and leads to the formation of the cyclohexadiene product.

An animation which form the diels-alder product form the transition state

The distances between the terminal carbons of cisbutadiene and those of ethene(the bonds that are about to form) were 2.21020Å and 2.20923Å, and the total energy was -231.60320816a.u.

HOMO and LUMO of the concerted transition state

The MOs were calculated by Gaussian and are shown below. They are both symmetrical.

The HOMO and LUMO of ethene (below) are opposite in symmetry to the HOMO and LUMO of butadiene- and so the symmetric LUMO of butadiene reacts with the symmetric HOMO of ethene and the anti-symmetric HOMO of ethene reacts with the LUMO of butadiene in the concerted mechanism. This analysis uses Frontier orbital thoery, which states that the most important reaction in pericyclic reactions are between the HOMO and LUMO and that interactions are FORBIDDEN between molecular orbitals with different symmetry.

An investigation into the regioselectivity of the Diels- Alder Reaction

For this analysis, unless otherwise specified the defautlt HF/321G basis set was used. The reaction between this cis-cyclohexadiene and maleic anhydride is notable because its analysis will give us an insight into the regioslectivity of the reaction.

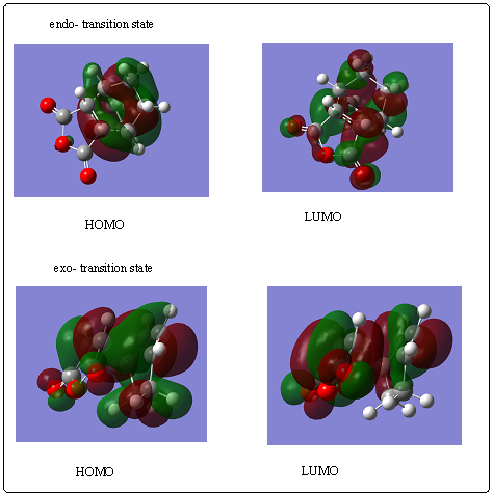
Two isomeric products are possible: the endo and exo- products, shown here. Only the endo- product forms experimenatlly, despite the fact that the exo- product is more thermodynamically stable due to a lower degree of steric hindrance. The endo- product must be the kinetic product- but why? Optimising both the endo- and exo- product using a 631G* basis set shows that the exo- product is indeed calculated as more stable by -5.7KJmol^-1. The transition state was optimised using the QST2 method, first specifying the endo- product as the product and then the exo- product. The transition states for the two reactions are compared below. The exo- product showed the following negative vibration at -643.70cm^-1.

Isomer	Total energy(hartree)	relative energy(KJ/mol)	dihedral angle between 'maleic anhydride' and 'cyclohexadiene' components(degrees)
exo-	-605.63547359	0	65.678
endo-	-605.6035912	5.7	169.023

The HOMO and LUMO MOs of the transition states are shown below. Although they are much more complex than for the reaction between ethene and cis-butadiene, the reason for the preference for an endo- transition state can be seen more clearly as the electronic repulsion and steric hindrance in the exo- TS can be seen. A 'secondary orbital effect' (defined as the positive overlap of a nonactive frame in the frontier molecular orbitals of a pericyclic reaction' has been cited as one of the reasons for preferential endo- formation- non-active carbons stabilise the interacting HOMO and LUMO in the endo- adduct.However studies suggest that the reason for endo- preference is probably steric rather than electronic, especiall when there are no methyl groups on the reactants to add to the electronically favourable effect, and the MOs I calculated back this up.