Transition states and reactivity

Introduction

In this experiment, we used three pericyclic reactions to understand the transition states. Transition states could be identified through the potential energy surface, which shows that the energy of a molecule acts as a function of molecule's geometry. Generally, the number of geometric degrees of freedom of the non-linear molecule is equal to the dimensionality of its PES. This obey the equatoin (3N-6), where N= number of atoms.

Nf710 (talk) 00:13, 12 January 2018 (UTC) We choose this to be the case. We could choose other basis but then there would be linear dependancies.

In the PES, reactants and products locate at minimum points while the saddle(maximum) points represents the transition state. At saddle points, the gradient equals to zero and all forces vanish. Since the value of first derivatives of both minimum and maximum points are equal to zero, the second derivatives is needed to differentiate these two points. When the second derivatives is positive, it suggests the minimum point and once the geometry is changed, the energy will increase. In contrast, negative second derivatives leads to the transition state and the energy will decrease in the pathway to the product.

For non-linear molecules, their vibration modes also associate with the equation 3N-6 and each mode has its own force constant. After doing the optimisaition calculations, there should be only one imaginary frequency. It proves that we have the transition state structure because the imaginary frequency aries from the negative curvature of the 3N-6 dimensions of the PES at transition state.

Nf710 (talk) 00:13, 12 January 2018 (UTC) Ok you are almost there in your explanation. essentially at a miniumum all the second derivatives are positive (positive curvature). where at a TS all the second derivatives are psotive except 1 which is negative and this is the reation coord. The second derivatives in N dimensions can be obtains as the eigen values of the Hessian Matrix.

Method

In the following three exercises, all the transition states were obtained through optimisation of products. First, drawing the product structure in the GaussView and let the structure being optimised to minimum at semi-empirical PM6 level. If the optimisation went correctly, the frequencies should be all positive value. Then, breaking the bonds that were formed in the reaction, adjusting and 'freezing' those bonds to a certain length. For instance, setting C-C=2.2 Å, C-O=2.0 Å and C-S=2.4 Å. At the same time, fixing the coordinates of the atoms that related to the breaking bonds. After these, the structure was optimised again at PM6 level followed by a futher optimisation, which was run to obtain the TS. Once we got the TS, there should be only one imaginary frequency and a perfect IRC figure was obtained to make sure that the TS was correct (gradient = 0 at TS).

Exercise 1

(Fv611 (talk) Good job on the whole exercise, a shame that you forgot to show the bond forming vibration on the TS!)

For exercise 1, butadiene and ethlyene were used to do diels-alder reaction.

Optimization

Butadiene

Ethlyene

Transition State

Product

Table 1. optimisation at PM6 level

IRC and frequency calculation analysis

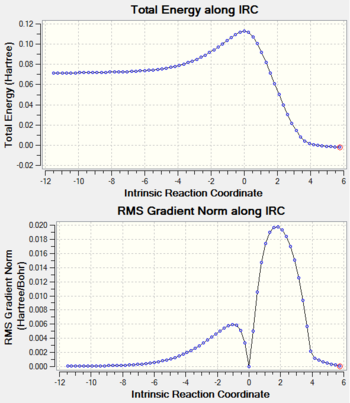
The figure below suggests that the correct TS is got because only one imaginary frequency was obtained and when the value of IRC in RMS gradient along IRC equals to zero, the gradient=0 as well. In addition, we found that the formation of the two bonds in DA reaction is a synchronous procedure.

Molecular orbital analysis

The following table shows the HOMO/LUMO of reactants and transition state.

Table 2. HOMO/LUMO and MO diagrams
	Butadiene	Ethylene	Transition state	Transition state
HOMO	HOMO of Butadiene, MO11	HOMO of Ethylene, MO6	HOMO of the TS, MO17	HOMO-1 of the TS, MO16
LUMO	LUMO of Butadiene, MO12	LUMO of Ethylene, MO7	LUMO of the TS, MO18	LUMO+1 of the TS, MO19

Only the orbitals that have the same symmetry can combine with each other to give the transition state MO because if the orbitals are miss matching, the overlap will be zero. Figure below was the idealized MO diagram for the reaction between butadiene and ethylene. The HOMO - LUMO interaction are summarised below: (S and AS are symmetric and asymmetric respectively)

 Ethylene LUMO (MO7, AS) - Butadiene HOMO (MO11, AS) ---> TS LUMO+1 (MO19, AS)
 Ethylene LUMO (MO7, AS) - Butadiene HOMO (MO11, AS) ---> TS HOMO-1 (MO16, AS)
 Ethylene HOMO (MO6, S) - Butadiene LUMO (MO12, S) ---> TS LUMO (MO18, S)
 Ethylene HOMO (MO6, S) - Butadiene LUMO (MO12, S) ---> TS HOMO (MO17, S)

The effect arise from the symmetry of the orbital on the orbital overlap integral:

 symmetric-antisymmetric interaction     ---> Zero
 symmetric-symmetric interaction         ---> Non-zero
 antisymmetric-antisymmetric interaction ---> Non-zero

In this experiment, butadiene and ethylene were doing [4+2] cycloaddition, which is a pericyclic chemical reaction. For pericyclic reactions, we have to obey the Woodward-Hoffmann Rules. The rules state that in order to make the reaction to be thermal allowed, the sum of (4q+2)s and (4r)a must be odd, where 's' represents suprafacial, 'a' stands for antarafacial and q,r are integers from 0. If the sum of (4q+2)s and (4r)a is an even number, then the reaction will be forbidden. According to the MO, we know that the cycloaddition between butadiene and ethylene was thermal allowed because :

  (4q + 2)s + (4r)a
  = 1 + 0
  = 1  ----> odd number, q=0,r=0.

Bond lengths analysis

The typical C-C bond lengths are shown below:

 sp³ C- sp³ C   1.54Å
 sp² C- sp² C   1.47Å
 sp³ C- sp² C   1.50Å

Table 3. C-C Bond lengths changes during the reaction
molecules	Bond lenghts	molecules	Bond lengths
	reactant ethylene C1=C4 1.33Å		reactant butadiene C12=C14 1.33Å C12-C10 1.47Å C10-C7 1.33Å
	Product C7-C1 1.54Å sp3-sp3 C1-C4 1.53Å sp3-sp3 C4-C14 1.54Å sp3-sp3 C14-C12 1.50Å sp3-sp2 C12=C10 1.34Å sp2-sp2 C10-C7 1.50Å sp2-sp3		Transition state C1=C4 1.38Å bond rupture C12=C10 1.41Å bond formation C10=C7 1.38Å bond rupture C7-C1 2.11Å bond formation C12=C14 1.38Å bond rupture C14-C4 2.11Å bond formation

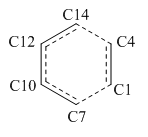
The Van der Waals radius of the C atom is 1.7Å, so the expected VDW C-C bond length shoule be 3.4Å. After comparing, we can see that the length of the partly formed C-C bonds (C14-C4 and C7-C1) in TS are smaller than the expected one while larger than the typical sp³ C- sp³ C bond length. It shows that the bond is forming. In addition, in TS, a partial double bond is formed between C12 and C10, as a result, the length of C12-C10 is smaller than the standard sp² C- sp² C bonds.

Exercise 2

In exercise 2, we looked at the reaction between cyclohexadiene and 1,3-dioxole.

Optimisation at B3LYP/6-31G(d) level

Structure

Frequency

Cyclohexadiene

1,3-Dioxole

Exo TS

Exo Product

Endo TS

Endo Product

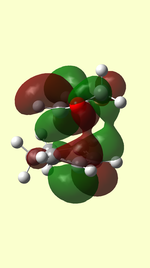
HOMO/LUMO of Transition State

Table 4. HOMO/LUMO of TS
	TS HOMO MO41	TS LUMO MO42	TS HOMO-1 MO40	TS LUMO+1 MO43
ENDO
EXO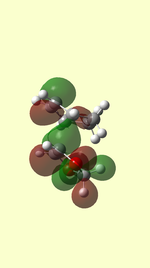

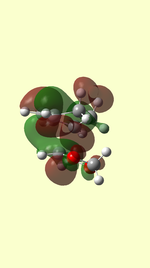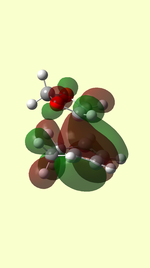Molecular Orbital Analysis

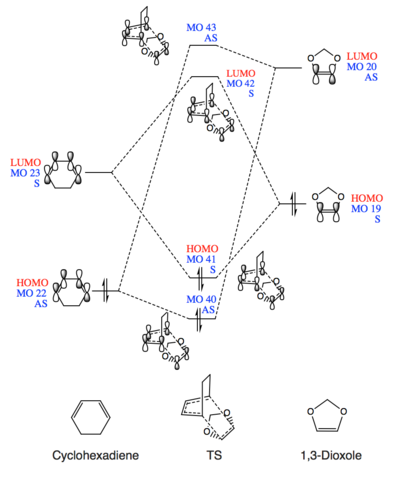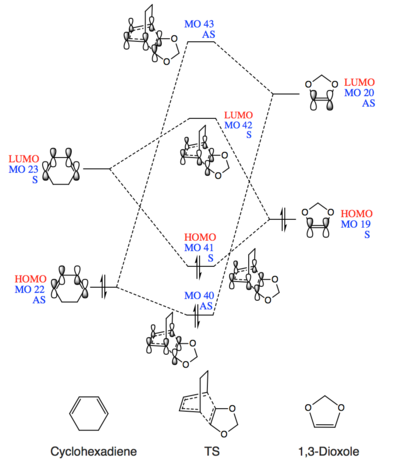Fig.1 MO diagram of ENDO TS	Fig.2 MO diagram of EXO TS

(Fv611 (talk) These are good MO diagrams, but the relative energies are slightly wrong, as for both the exo and endo cases the lowest energy orbital is the HOMO of the diene, and not the HOMO-1 of the TS. Well done on including the differences in relative energies in the exo and endo diagrams, but you could have added a little discussion about those differences.)

There are two types of Diels–Alder reaction, one is the standard DA reaction, the other is inverse electron demand DA reaction. Generally, for most of the DA reactions, MOs of the electron rich diene would have higher energy levels than the MOs of electron poor dienophile. Then, according to the frontier molecular orbital theory, there are interactions between the HOMO of diene and LUMO of dienophile because their energy levels are close to each other. In contrast, for inverse electron demand DA reactions, the energy of diene's LUMO is more similar to the dienophile's HOMO. As a result, in the inverse situation, LUMO_diene and HOMO_dienophile are the frontier molecular orbitals.

In both MO diagrams (Fig.1 and Fig.2), the energy levels of HOMO/LUMO of the diene (cyclohexadiene) are lower than the ones of dienophile (1,3-dioxole). Also, the FMO are LUMO_{cyclohexadiene}(MO 23) and HOMO_1,3-dioxole (MO 19). The small energy gap between them lead to the strong interactio and favourable the bond formation. These indicate that cyclohexadiene and 1,3-dioxole will do an inverse electron demand DA reaction.

~~.~~ This is a correct conclusion however you could have demonstrated this quantiatively by doing an energy calculation with both reactants on the same PES and looking at the orbtials

Thermochemistry - Reaction Energies and Barriers

The following energies' units are converted from Hartree. (1 Kjmol^-1 = 3.8088 X10^-4 Hartree)

Table 5. Energies of reactants, products, TS
Molecules	Energies under B3LYP/631G(d) mode / Kjmol^-1
Cyclohexadiene	-6.12582 x 10⁵
1,3-Dioxole	-7.01158 x 10⁵
ENDO TS	-1.313614 x 10⁶
ENDO product	-1.313815 x 10⁶
EXO TS	-1.3136 x 10⁶
EXO product	-1.3138 x 10⁶

In order to get the reaction energy and activation energy, we need to use the following equations:

 Reaction energy = Product's energy - Reactants' energies
 Activation energy = TS's energy - Reactants' energies

Table 6. E_activation and E_reaction of Endo/Exo product
	Activation Energy / Kjmol^-1	Reaction Energy / Kjmol^-1
Exo Product	+140.0	-60.0
Endo Product	+126.0	-75.0

After comparing the data in table.6 we can see that the Exo product has more positive E_activation than the Endo one, with +14Kjmol^-1. At the same time, the E_reaction of Endo product has more negative value (-15Kjmol) than the Exo one. The lower the activation energy, the faster the reactants can reach the TS and fewer energy is needed. Therefore, smaller E_activation means the product is kinetically favourable and in this exercise, endo product is the kinetically favourable one. The reaction energy represents the stability of the product. More negative the reaction energy is, more heat is released to the environment to form the stable product. As a result, the endo product is thermodynamically favoured as well.

Secondary Orbital Interaction

Both secondary orbital interaction and primary orbital interaction can be seen in the endo TS while in exo TS, only primary orbital interaction presents. The secondary orbital interaction indicates that the lone paired electrons in p orbitals on oxygen will overlap with the LUMO_diene. As a result, the endo approaching is more preferred. Also, because of the SOI, the activation energy is decreased and then, the TS is stabilised. When the dienophile doing exo approach, sterics effect arose, which lead to a larger reaction barrier energy.

Your energies are not correct sadly. However you have stll come to the correct conclusions. you could however have back up your points with diagrams which would have made it much clearer.

Exercise 3

Exercise 3 is the DA cycloaddition of Xylylene and SO₂.

Optimisation at PM6 level

Xylylene

EXO TS

ENDO TS

Cheletropic TS

SO₂

Exo Product

Endo Product

Cheletropic Product

Table 7. Optimisation of reactants, transition states, products at PM6 Level

(Make sure you know what's going on when you copy code for a different purpose. These molecules either are at an intermediate geometry or are vibrating at a random normal mode. You must check that the script is doing what you want it to do Tam10 (talk) 15:00, 9 January 2018 (UTC))

IRC calculation

Reaction	gif	IRC
EXO DA reaction
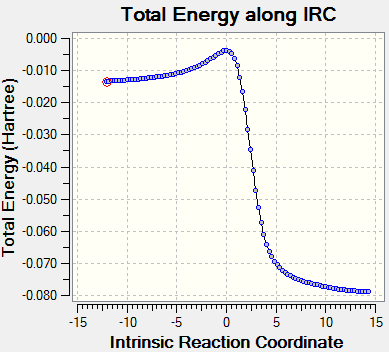
ENDO DA reaction
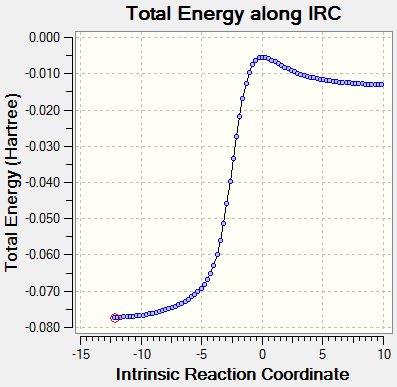Cheletropic

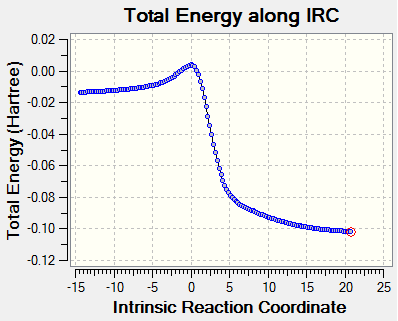
Since the xylylene has two cis-diene in its structure and both of them can do the cycloaddition reactions with dienophiles, we said that it is highly reactive. The gif above showed the trajectories of the three reactions. As it showed in the graph, when the six-membered ring is forming, aromatic ring arose because the lone pairs on oxygen and sulfur is participating and further stable the structure.

(Any justification for the energetic ordering? Tam10 (talk) 15:00, 9 January 2018 (UTC))

Activation and reaction energies

The following energies' units are converted from Hartree. (1 Kjmol-1 = 3.8088 X10-4 Hartree)

Table 9.Activation and reaction energies at PM6 Level/kjmol^-1
Molecule	Exo approach	Endo approach	Cheletropic
xylylene	+469.287	+469.287	+469.287
SO2	-313.143	-313.143	-313.143
Transition State	+241.748	+237.770	+260.085
Product	+56.214	+56.973	+0.0131
Activation Energy/kjmol^-1	+85.604	+81.626	+103.941
Reaction Energy/kjmol^-1	-99.930	-99.171	-156.131

According to Table.8 we can see that the cheletropic reaction has the most negative value of reaction energy, which means it is the most exothermic reaction among these three reactions followed by DA exo pathway and endo pathway. In addition, the DA endo pathway has the lowest activation followed by exo pathway and cheletropic reaction. Therefore, in comparison, the cheletropic product is thermodynamic favoured and the endo product is kinetically favoured. The endo product is slightly less stable than the exo one because there is more steric replusion.

Reaction profile

Energy Profile of three reactions.

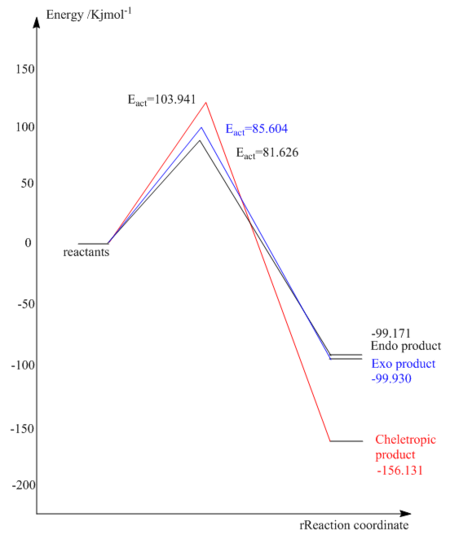Conclusion

The transition states of different DA/Cheletropic reactions were investigated through the experiment by using GaussView. In each exercise, the experimental product was optimised to minimum at semi-empirical PM6 level, changed the breaking-bond distance, optimised to minimum again and then, optimised to the TS. All the TS structures were checked with their frequency calculation and IRC. Since each TS structure that we got has only one imaginary frequency, we said that those structures were obtained correctly. The IRC presented the pathway of reactants in DA reactions and indicated that the formation of the two bonds are synchronous. Also, through exercise 2 we could know that when there is an inverse demand DA reaction, the frontier molecular orbitals of this kind of reaction will be the HOMO of dienophile and the LUMO of diene. Furthermore, the products could be classified into two types: thermodynamically favored one (when the reaction has larger reaction energy) and kinetically favored one (when the reaction has samller activation barrier).

Log Files

Exercise 1

IRC:File:EX1 PRODUCT IRC.LOG

Exercise 2

Cyclohexadiene at PM6 level:File:ZkwCYCLO PM6.LOG
Exo TS at PM6 level:File:ZkwEXO TS PM6-3.LOG
Endo TS at PM6 level:File:ENDO TS PM6.LOG

Exercise 3

Reference

Atkins & De Paula Physical Chemistry, 9 edn., 2010.
Rooshenas, Parham; Hof, Kira; Schreiner, Peter R.; Williams, Craig M. (1 February 2011). "1,2,4-Triazine vs. 1,3- and 1,4-Oxazinones in Normal- and Inverse-Electron-Demand Hetero-Diels-Alder Reactions: Establishing a Status Quo by Computational Analysis". European Journal of Organic Chemistry.