Rep:Mod:KZ1015
NH3 molecule
N-H bond length/Angstroms = 1.01798
H-N-H bond angle = 105.741°
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final energy E(RB3LYP): -56.55776873 a.u.
RMS Gradient Norm: 0.00000485 a.u.
Point Group: C3V
[The optimisation file is linked to here]
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986272D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
ammonia molecule. |
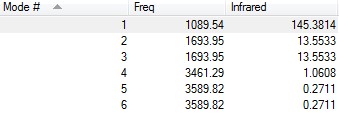
Vibrational analysis of NH3 molecule
The vibrational modes are shown below:
According to the 3N-6 rule, NH3 has 6 vibrational modes.
The second mode and the third mode have the same energy, while the fifth and the sixth mode generate the same energy as well. The modes that have the same energy are called as degenerated modes.
Mode 1,2,3 are "bending" vibrations and mode 4,5,6 are "bond stretch" vibrations.
Among these modes, the fourth one is highly symmetric since the all the bonds stretches in the same trend.
Mode 1 is known as the "umbrella" mode because of its direction of bending, into and out of the screen.
In experimental spectrum, we are expected to see 2 bands of gaseous ammonia.
Since we did not get any negative frequency, there is no transition state.
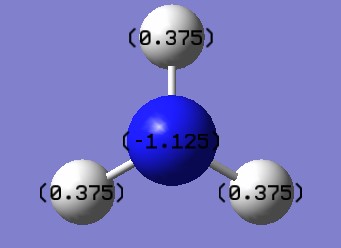
Charges analysis of NH3 molecule
Charge on N atom = -1.125
Charge on H atom = 0.375
We would expect to see negative charges on nitrogen atom and positive charge on hydrogen atom because nitrogen atom has higher electronegativity.
The Haber-Bosch process
The Haber-Bosch process is the industrial means by which nitrogen gas and hydrogen gas are converted to ammonia and ammonia is crucially important as a fertilizer.
The reaction proceed as the following equation:
N2 + 3 H2 → 2 NH3
N2 molecule
Bond length/Angstroms = 1.1055
Bond angle = 180°
Calculation Method: B3LYP
Basis set: 6-31G(d,p)
RMS Gradient Norm: 0.00000060 a.u.
Final energy E(RB3LYP): -109.52412868 a.u.
Point group:D∞h
[The optimisation file is linked to here]
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.400983D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
nitrogen molecule. |
Vibrational analysis of N2 molecule
Vibrational mode = 1
frequency = 2457.33Hz
Since there is no negative frequency, no transition state exist.
H2 molecule
Bond length/Angstroms = 0.74279
Bond angle=180°
Calculation Method: B3LYP
Basis set: 6-31G(d,p)
Final energy E(RB3LYP): -1.17853936 a.u.
RMS Gradient Norm: 0.00000017 a.u.
Point group: D∞h
[The optimisation file is linked to here]
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
hydrogen molecule. |
Vibrational analysis of H2 molecule
Vibrational mode = 1
frequency = 4465.68Hz
Since there is no negative frequency, no transition state exist.
Energies of Haber-Bosch process
E(NH3) = -56.55776873 a.u.
2*E(NH3) = -113.11553746 a.u.
E(N2) = -109.52412868 a.u.
E(H2) = -1.17853936 a.u.
3*E(H2) = -3.53561808 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)] = -0.0557907 a.u. = -146.5 kJ/mol
Gaseous reactants are more stable than ammonia product because the energy that released by gaseous nitrogen is much more than the ammonia product. It means more energy is needed to break the nitrogen bonds.
However, the literature value of this reaction is -92.4 kJ/mol, which is quite different with our calculated value. It shows that the method that we used are not suitable for calculating the final reaction energy of nitrogen and hydrogen.
S2 molecule
Bond length/Angstroms = 1.92943
Bond angle = 180°
Calculation Method: B3LYP
Basis set: 6-31G(d,p)
RMS Gradient Norm: 0.00000372 a.u.
Final energy E(RB3LYP): -796.32599779 a.u.
Point group:D∞h
[The optimisation file is linked to here]
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.000011 0.001800 YES
RMS Displacement 0.000016 0.001200 YES
Predicted change in Energy=-7.077711D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.9294 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
disulfur molecule. |
Vibrational analysis of S2 molecule
Vibrational mode = 1
frequency = 697.03Hz
Since there is no negative frequency, no transition state exist.
Charges analysis of S2 molecule
Both of the sulfur atoms have no charge on them because they have no diople moment.
Molecular orbitals of S2 molecule

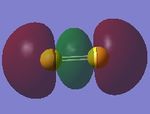


Two 3s AO of sulfur atoms contribute to this antibonding MO. The MO is higher in energy and occupied. These two 3s AO overlap and give a σ* bond.
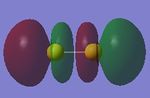
Two 3px AO of sulfur atoms contribute to this bonding MO. The MO is higher in energy and occupied. The two 3px AO overlap and give a π bond and it is in HOMO region.
Two 3px AO of sulfur atoms contribute to this antibonding MO. The MO is higher in energy and unoccupied. These two 3px AO overlap and give a π* bond.
Two 3py AO of sulfur atoms contribute to this bonding MO. The MO is higher in energy and occupied. The two 3py AO overlap and give a π bond and it is in HOMO region.
Two 3py AO of sulfur atoms contribute to this bonding MO. The MO is higher in energy and unoccupied. The two 3py AO overlap and give a π* bond.