Rep:Mod:KT1902

Introduction

Diels-Alder reactions are a sub-set of the more general cycloaddition reactions, which prove to be an indispensable tool in an organic chemist’s arsenal. This is because they can be used to generate, in excellent yields, cyclic compounds with a very well-defined stereochemistry. This well-defined stereochemistry in the cyclic products can be attributed to the concerted nature of the mechanism – the pathway leading from reactants to products occurs in a single step and goes through a single transition state. This excludes the possibility of forming any intermediates . Hence, computationally tracking the progress of reactants and products in cycloadditions is much easier as only one transition state structure needs to be found. Once the correct transition state structure is found, an intrinsic reaction coordinate (IRC) path can be calculated, which will provide the potential energy surface (PES) for the cycloaddition, and thus the magnitude of the activation energy barrier. This whole computational process allows analysis of the transition state, not possible via any experimental methods as the transition state is an energy maximum (more on this shortly) and thus cannot be isolated and characterised, as any manipulation of its structure will cause it to “decompose”.

The computational calculations used throughout are based on the Density Functional Theory (DFT), as opposed to the Hartree-Fock (HF) level of theory. Using the DFT decreases the time and complexity of the Gaussian 09W calculations as it encompasses a lower number of degrees of freedom (DoF). The Density Functional Theory functional is the electron density, which itself is only a function of x, y, and z (3 DoF). On the other hand, the Hartree-Fock theory deals directly with the many-particle wavefunction (dependent on nuclear and electronic positions), which is a function of 3N DoF (the coordinates of all N number of atoms in the system. In addition, the Born-Oppenheimer approximation, the footing of all computational theories, itself already reduces the number of DoF.

The computational methods and levels of theory used do have drawbacks. Firstly, in order to optimise to a TS using the Berny algorithm, the transition state structure had to be guessed which could prove very difficult for larger and more complex systems. This also means that new, unseen reactions could not be studied as the structure of the transition state would be unknown. Secondly, the calculations consider the whole system as one entity and so neglects any interaction energies between the multiple reactants. The one entity is treated like an ideal gas.

A potential energy surface (PES) describes the energy of a molecule as a function of the positions of its nuclei, r. However, a chemical reaction, and thus a PES, doesn’t depend on the absolute position of the nuclei, but rather their relative positions (internal degrees). Therefore, the translation and rotational dimensions of the system can be removed, leaving the PES to have 3N-6 dimensions. As Figure 1 shows, there are many reaction pathways leading from reactants to products, via transition states. A global minimum is the lowest energy point of the surface, taking into account all possible pathways, and represents the most thermodynamically stable structure. A local minimum is also an energy minimum, but occurs when all but one degrees of freedom are minimised. All minima have a positive curvature (the second derivative > 0) and a positive frequency of vibrational mode. A transition state is an energy maximum in a certain reaction pathway (all DoF are at a minimum except for one). The transition state for the lowest energy pathway has a negative curvature (the second derivative < 0) and so has a negative frequency.

Figure 1: A 3D PES emphasizing the saddle point and local and global energy points. Credit to http://sf.anu.edu.au/~vvv900/gaussian/ts/ for the image.

Please note: On a 2D PES, the transition state is represented by a saddle-point and so multiple second derivatives must be taken at points around the saddle to determine the direction of the reaction trajectory.

This page will explore, computationally, using Gaussian 09W, the mechanism of the Diels-Alder reaction between ethene and butadiene, as well as determining the thermodynamic and kinetic products of the more-complicated Diels-Alder reaction of cyclohexadiene and 1,3-dioxole. The reaction pathways and energies of the Diels-Alder will be compared to the Cheletropic mechanism.

Nf710 (talk) 22:00, 15 December 2016 (UTC) Very good overview of the methods, good basic understand. TS defined correctly

Exercise 1: Reaction of butadiene with ethene

Figure 2:Reaction scheme for the cyclo-addition of ethene with butadiene.

The [4+2] cycloaddition of ethene and butadiene represents an undecorated Diels-Alder reaction, and thus, any computational analysis of this is also simple. Undecorated because the diene and dienophile do not possess any substituents that are electron-withdrawing or electron-donating. An electron-withdrawing group would lower the energy of the dienophile LUMO. An electron donating group would raise the energy of the diene HOMO. Combined, these effects would cause a better overlap of the frontier orbitals in the transition state (TS). However, these effects are not present in this example and so there is a poor orbital overlap (large energy gap) between the ethene and butadiene, leading to poor reactivity. It is known that the reaction proceeds via a concerted mechanism but we will investigate whether it is a synchronous or an asynchronous process.

MO diagram of ethene and butadiene

The frontier MOs, generated from the linear combination of atomic orbitals of each atom, of both reactants were assigned subscript symmetry labels. These symmetry labels describe the phase pattern of the MOs, under the inversion operation – if the MOs are symmetrical with respect to inversion, they are given the label “g” for “gerade”, if they are asymmetrical, they are allocated the label “u” for “ungerade”. As can be seen in Figure 5, only the MOs of ethene and butadiene that will interact will be those which provide the best orbital overlap in the TS. The orbital overlap (S) in the TS will be maximised if the constituent MOs are close in energy and are of the same symmetry. Hence, the best orbital overlap that can be achieved here is between the HOMO of butadiene with the LUMO of ethene; and between the LUMO of butadiene and the HOMO of ethene. The other butadiene MOs don’t interact because they are either of different symmetry, or they are too different in energy. The orbital overlap (S) between MOs (described by wavefunctions) on fragment A and MOs on fragment B eluded to earlier is described mathematically by the formula:

${\mathbf{S}}_{\mathrm{A}\mathrm{B}}=\int {\mathrm{\Psi }}_{\mathrm{A}}^{*}{\mathrm{\Psi }}_{\mathrm{B}}dV,$

Therefore, the overlap between orbitals of opposing symmetries (“u” with “g”) will result in S = 0 as any bonding interaction between the MOs will be cancelled out exactly by an antibonding interaction. This would be a forbidden interaction. Only the interaction between the same symmetry orbitals (so “g” with “g”; and “u” with “u”) will give a value of S that is non-zero. This would be an acceptable interaction and so would proceed. These symmetry rules will be applied throughout all of the exercises.

Figure 3: Ethene HOMO.

Figure 4: Ethene LUMO.

Frontier orbitals of butadiene

Figure 5: MO diagram for the reaction of ethene with butadiene.

MOs of the TS of the cycloaddition between ethene and butadiene MOs for the Diels Alder reaction

Mechanism: To synchronous or not to synchronous?

Examination of the transition state allows us to confirm that the reaction occurs via a concerted mechanism. From this, the mechanism’s synchronous/asynchronous nature can be determined. The transition state was found using a semi-empirical PM6 method, optimized using the Berny algorithm, with force constants allowed. A vibrational frequency analysis can be performed on the structure obtained to prove that it is the correct TS structure. A correct TS structure should have one negative vibrational mode, as it is the energy maximum. This negative frequency portrays the formations of the new C-C bonds. The table below summarizes the changes in the bonds as the reaction coordinate proceeds from reactants to products, via the TS. In the table, “2 x VdW” signifies the sum of the van der Waals radius of two adjacent carbon atoms. It is their internuclear distance, prior to their mutual bond formation, and so is longer than a C-C single bond and a C=C double bond. As a reference point, the literature values for: Van der Waals radius of a carbon atom, 1.680 Å ; an sp³ C-C bond, 1.537 Å; an sp² C=C bond, 1.347 Å

Figure 6: Labelled carbons in the TS and in the product.

Bonds between carbons…	Bond lengths in reactant (Å)	Type of bond	Bond lengths in TS (Å)	Bond is … during reaction	Bond lengths in product (Å)	Type of bond
1,2	1.33539	sp2	1.37978	lengthening	1.50090	sp3
2,3	1.46834	sp3	1.41107	shortening	1.33784	sp2
3,4	1.33539	sp2	1.37978	lengthening	1.50090	sp3
4,5	3.41334	2 x VdW	2.11461	shortening	1.54040	sp3
5,6	1.32736	sp2	1.38177	lengthening	1.54091	sp3
6,1	3.41425	2 x VdW	2.11469	shortening	1.54041	sp3

The newly-forming C1-C6 and C5-C4 σ bonds in the TS structure have an internuclear distance of 2.114 Å which is less than 1.5x the VdW radius of a carbon atom – indicating that the two carbon atoms are close enough for orbital interactions to occur as the reaction proceeds. From the tabulated data, it can be confirmed that the cycloaddition reaction between ethene and butadiene proceeds in a synchronous manner as both of the newly-forming σ bonds (C1-C6 and C5-C4) have exactly the same length in the TS structure. This observation is further reinforced by the bond lengths between C1-C2 and C3-C4, which are both turning into sp3 bonds, also being the same length. This corroborates that the concerted mechanism is synchronous as it shows that the breaking and forming of bonds occurs at the same rate at all positions around the ring. The synchronicity can also be seen in the negative vibrational frequency of the TS, Figure 7. In addition, as the reactants are simple and symmetrical themselves, there is no logical preference for them to undergo an asynchronous mechanism.

Figure 7: Animation of the negative vibrational frequency in the TS. Wavenumber = -526.70 cm-1. It illustrates the formation of the new C-C σ bonds that form at the termini of the butadiene and the ethene.

Figure 8: Animation of the lowest positive vibrational frequency in the TS. Wavenumber = +136.16 cm-1.

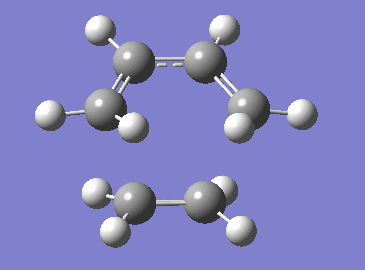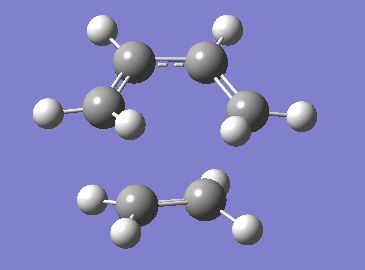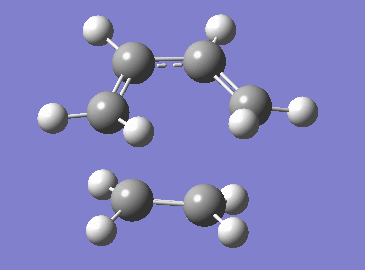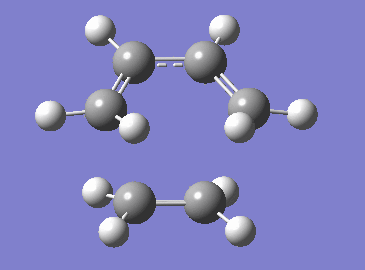The negative vibrational frequency shows an out-of-plane stretch for both reactant molecule. The synchronous nature of the cycloaddition can be seen in the animation in Figure 7. It shows the simultaneous C-C σ bond formation. In comparison, the lowest positive frequency vibration corresponds to an in-plane bend of both of the reactant molecules. It is clear that this vibration does not lead to the formation of the σ bonds as at any one point, one of the ethene carbon atoms is too far from the butadiene terminal carbon atoms.

Woodward-Hoffman analysis

Figure 9: Reaction coordinate of ethene reacting with butadiene.

Figure 10: Woodward-Hoffmann analysis of the thermally allowed cycloaddition.

The height difference between the reactants and the TS represents the activation energy for this Diels-Alder reaction. This activation energy barrier is overcome usually by thermal energy. If this is possible, it is said the reaction is “thermally allowed” by virtue of the Woodward-Hoffman rules, which states that the sum of the (4q+2) suprafacial and (4r) antarafacial components must be odd, where q and r are both integers, as we have here.

Exercise 2: Reaction of Cyclohexadiene and 1,3-dioxole

Figure 11: Reaction scheme for the cyclo-addition of cyclohexadiene with 1,3-dioxole. It highlights the two different pathways, which arise from the two possible geometries of the 1,3-dioxole.

This next Diels-Alder reaction opens up the doors to a new level of complexity – the dienophile can now adopt two different geometries relative to the diene prior to the cycloaddition. This means that now two different transition state structures are possible, leading to two different product conformations. The two different pathways, the exo and endo pathways, as well as the different approach trajectories of the two reactants are shown in Figure 11. The different approach trajectories enable the possibility of secondary orbital interactions which will result in different activation energies for the different pathways.

The control of stereochemistry here is a vital aspect of executing a graceful synthesis and so by finding out the activation energy of each separate pathway, you can tailor the reaction conditions to selectively yield a specific product conformation.

MO analysis

Figure 12: An example of a normal electron demand MO interaction.

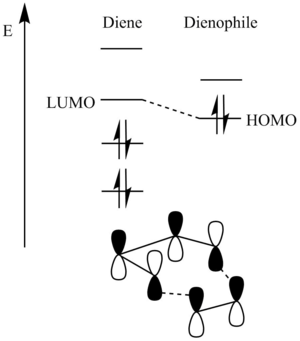
Stereoelectronics emphasizes the importance on focusing on the frontier MOs (the best donor and the best acceptor orbitals) and so all other MOs will be ignored to simplify the analysis. As was seen in the cyclo-addition between ethene and butadiene, the energy gaps between the ethene LUMO and the butadiene HOMO were roughly equal to the energy gap between the ethene HOMO and butadiene LUMO. Thus, both of their respective interactions were just as energetically favourable. However, here, the presence of the electron-donating oxygens (from the ether functional group) on the 1,3-dioxole increases the energy of both of its HOMO and LUMO. The dienophile’s filled π-orbital’s energy was raised sufficiently enough to allow it to be the reacting HOMO. The energy of the cyclohexadiene frontier MOs isn’t changed much as there are no strong electron-donating/ no strong electron-withdrawing groups attached. The sp³ hybridised carbons, attached at the termini of the diene, aren’t electron-donating enough to change the ordering of the diene MOs relative to the dienophile MOs and so can be ignored. This effect results in a smaller energy gap between the diene LUMO and the dienophile HOMO. Their interaction will be the most favourable, and will have the best orbital overlap, and so this will be the main bonding interaction in the TS. This, therefore, is an inverse electron-demand Diels-Alder reaction.

Frontier MOs of 1,3-dioxole

Frontier MOs of cyclohexadiene

Thermochemical analysis

Nf710 (talk) 22:50, 15 December 2016 (UTC) Correct energies. Good understanding about the demand of the reaction, its a shame you got the exo and endo mixed up.

TS from ... pathway	Energy of reactants (kJ/mol)	Energy of TS (kJ/mol)	Energy of the product (kJ/mol)	Activation energy barriers (Ea) (kJ/mol)	Reaction energies (ΔGr) (kJ/mol)
Exo	0	157.36	-65.09	+157.36	-65.09
Endo	0	165.81	-67.75	+165.81	-67.75

A B3LYP/6-31(d) level of optimisation was run on the geometries of the reactants, products and TS from each pathway, on top of the PM6 optimisation level which preceded. The energy values for the reactants, TS structures and products, from the PM6 level, were relatively the same as that for the B3LYP/6-31(d) level. However, the absolute values were different. The trade-off in accuracy of values (the semi-empirical PM6 level of optimization is less accurate) and the time taken to run the calculations (the B3LYP/6-319d optimization method is more time-consuming) must be considered. The energies of the reactants are set to zero because: firstly, it is subsequently easier to analyse the energies of the TS and products, relative to zero; and secondly, it represents the more accurate situation where at infinite separation and in the gas phase, the cyclohexadiene and the 1,3-dioxole are hard spheres as they are not interacting.

The tabulated data shows that the exo pathway is under kinetic, irreversible control – it has a lower activation energy barrier; and the corresponding exo product is not as thermodynamically stable as that of the endo pathway. It’s described as the kinetic product. The endo pathway, on the other hand, is under thermodynamic, reversible control. It has a larger activation energy barrier but the resulting product is more thermodynamically stable. It’s described as the thermodynamic product. Now, the same number and same type of bonds are present in the kinetic as in the thermodynamic product, so it can be concluded that the extra stabilisation of the thermodynamic product arises from the orbital overlap.

Figure 13: The secondary orbital interactions available in the exo-TS and not in the endo-TS.

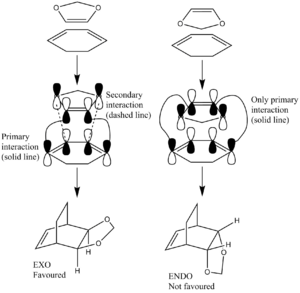
As can be seen in Figure 13, in the exo pathway, there is a possibility for secondary orbital overlap. There are secondary (non-bonding) orbital interactions in the exo- TS, between the oxygen p-orbitals and developing π-bond in the cyclohexadiene. These interactions statbilise the TS, reducing the activation energy barrier, making the exo- product faster to obtain. Hence, the exo-product is the kinetic product. These interactions are not possible in the endo- TS and so the benefits aren’t gained there. The primary (bonding) interactions are present in both pathways. The exo product is more thermodynamically stable as there is less steric strain having the one carbon bridge eclipsing the dioxole ring then having the two carbon bridge eclipsing it, as in the endo product. The stabilisation from the secondary orbital interactions outweigh the increased steric strain.

(In Figure 13 you have endo and exo mixed up, but it's the right way around in the Jmols below Tam10 (talk) 15:11, 6 December 2016 (UTC))

Frontier MOs for the endo TS

Frontier MOs for the exo TS

Exercise 3: Diels-Alder vs. Cheletropic: o-Xylylene-SO₂ cycloaddition

Figure 14: Showing all five possible reaction pathways of SO₂ with o-Xylylene.

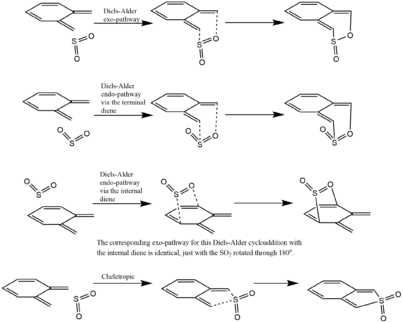
(Bonding for products in Fig 14 is wrong Tam10 (talk) 15:11, 6 December 2016 (UTC))

Cheletropic reactions are a different sub-set of cycloadditions to the classic Diels-Alder [4+2] cycloaddition. In a cheletropic cycloaddition, the "two new σ bonds which terminate at a single atom are made, or broken, in concert".

The reaction of SO₂ with o-Xylylene is open to 5 different reaction pathways, as can be seen in Figure 14. As defined, the cheletropic reaction of the two leads to the formation of a five-membered ring, from the terminal diene of the o-Xylylene and the S atom of SO₂. As studied in Exercise 2, the hetero-Diels-Alder cycloaddition can occur via two possible paths, the exo- and endo- pathway, both of which have a different TS energy and different product energy, due to the secondary orbital interactions studied before. These three reaction pathways will be studied collectively so that their activation energies and products energies can be compared. The structures of each of their TS will have to be found to perform this thermochemical analysis. Ergo, the TS structures were optimized using the semi-empirical PM6 level, along with the Berny algorithm. The validity of each TS was checked to have the correct single negative vibrational frequency (which corresponded to the formation of the two new σ bonds).

Furthermore, there is a second diene functional group in the o-Xylylene molecule, which is in the ideal s-cis conformation for a hetero-Diels-Alder cycloaddtion. This too can undergo the two separate exo- and endo- pathways, giving rise to five total possible reaction pathways.

Intrinsic Reaction Coordinates

Figure 15: Animation of the negative vibrational frequency in the TS of the cheletropic pathway. It illustrates the formation of the new C-C σ bonds that form at the termini diene of o-Xylylene and the S of SO2.

Figure 16: Animation of the negative vibrational frequency in the TS of the endo-Diels-Alder pathway. It illustrates the formation of the new C-C σ bonds that form at the internal diene of o-Xylylene and the S and one O of SO2. The alternate exo-pathway is the same but with the SO2 rotated through 180o.

Figure 17: Animation of the negative vibrational frequency in the TS of the endo-Diels-Alder pathway. It illustrates the formation of the new C-C σ bonds that form at the terminal diene of o-Xylylene and the S and one O of SO2.

Figure 18: Animation of the negative vibrational frequency in the TS of the exo-Diels-Alder pathway. It illustrates the formation of the new C-C σ bonds that form at the terminal diene of o-Xylylene and the S and one O of SO2.

Figure 19: Reaction coordinate for the cheletropic pathway.

Figure 20: Reaction coordinate for the Diels-Alder endo-pathway via the internal diene of o-Xylylene. The alternate exo-pathway is negligibly different.

Figure 21: Reaction coordinate for the Diels-Alder endo-pathway via the terminal diene of o-Xylylene.

Figure 22: Reaction coordinate for the Diels-Alder exo-pathway via the terminal diene of o-Xylylene.

As the animations above show, all of the reaction pathway mechanisms are slightly asynchronous, but still concerted. In the Diels-Alder cycloadditions, at the transition state, the carbon-oxygen σ bond formation is more advanced than the carbon-sulfur σ bond formation. This is because carbon and oxygen are in the same period of the Periodic Table and so will have similar sized orbitals, leading to better overlap. The sulfur, on the other hand, is a period below carbon and so will have a much bigger, more diffuse orbital, leading to poorer orbital overlap. In the cheletropic cycloaddition, one of the carbon-sulfur σ bonds forms faster than the other. If the diene and dienophile were asymmetrical, this asynchronicity would give rise to regioselectivity.

Thermochemical analysis

By only looking at the reaction schemes of the five possible reaction pathways, not much can be judged on whether the reaction is actually feasible/will occur. Thus, this thermochemical analysis determines the activation energies of each pathways, as well as their overall reaction energies. This will give light to which pathway is under thermodynamic control and which is under kinetic control. The activation energies were the difference in energies between the optimized (semi-empirical PM6 level of optimization) reactants and TS structures. The reaction energies were the difference in energies between the optimized (semi-empirical PM6 level of optimization) reactants and products.

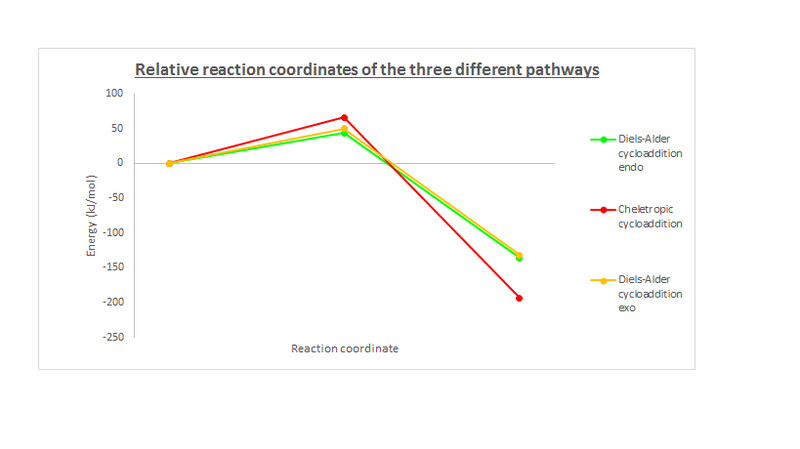
Reaction pathways	Activation energies (Ea) (kJ/mol)	Reaction energies (ΔGr) (kJ/mol)
Diels-Alder endo-pathway via the terminal diene	+43.25	-135.95
Diels-Alder exo-pathway via the terminal diene	+50.06	-131.98
Diels-Alder endo-pathway via the internal diene	+87.99	-8.55
Diels-Alder exo-pathway via the internal diene	+71.04	-11.32
Cheletropic cycloaddition	+65.66	-193.19

Figure 23: Relative reaction coordinates of the three reaction pathways.

The reactant energies were set to zero as firstly, the relative energies of the three pathways are more informative than the absolute values; and secondly, the reactants were treated as hard spheres at infinite separation and so are assumed to have zero interaction energy. This is supported by the ideal gas law, as this reaction occurs in the gas phase.

(If the reactants are in vacuum, their volume doesn't really need to be considered Tam10 (talk) 15:11, 6 December 2016 (UTC))

From the thermochemical data, we can conclude that, in fact, only 3 of the possible 5 reaction pathways will actually occur. The relatively high activation energies and the low reaction energies of the cycloaddition via the internal o-Xylylene prove it to be very thermodynamically (the product is not much more stable than the reactant) and very kinetically (high activation energy) unfavourable. Thus, it will not be occuring and will not be a competing reaction pathway. As mentioned, the product, from the Diels-Alder pathway via the internal diene, is more stable than the reactants but this net stabilisation (of 8.55 kJ/mol for the endo-pathway and 11.32 kJ/mol for the exo-pathway) is minute compared to the net stabilisation of the other three pathways. This, in conjunction with the high activation energy barrier, compared to the other three pathways, makes the reaction pathway involving the internal diene very unfavourable and a poor contender.

(There are 6 pathways including the internal cheletropic reaction Tam10 (talk) 15:11, 6 December 2016 (UTC))

Putting the internal diene reaction pathways aside, it can be seen that the cheletropic cycloaddition yields the thermodynamic product (lowest reaction energy of -193.19 kJ/mol) and with the highest activation energy barrier of the three (with 65.66 kJ/mol), this pathway is under thermodynamic, reversible control. The more thermodynamically stable cheletropic product is due to the formation of a less strained ring system - sulfur is larger than carbon. The higher activation energy can be attributed to the formation of a five-membered ring as opposed to a less strained six-membered ring.

On the other hand, the Diels-Alder cycloaddition pathway is under kinetic, irreversible control. This was concluded from the low activation energy barrier for this pathway. The endo-pathway variant of the Diels-Alder cycloaddition here is favoured over the exo-pathway. The endo-pathway has a lower activation energy of 43.25 kJ/mol compared to 50.06 kJ/mol of the exo-pathway and so the endo-product is the kinetic product. This is due to the secondary orbital interactions between the p-orbital of the oxygen (outside of the ring) feeding electron density into the developing π-bond in the o-Xylylene fragment, stabilising its transition state. The exo-TS doesn't have these secondary orbital stabilising interactions but its product has less steric strain. The stabilisation from the secondary orbital interactions outweigh the increased steric strain.

Instability of o-Xylylene

Figure 24: The possible intramlecular Diels-Alder cycloaddition of o-Xylylene.

Because of diene nature, o-Xylylene is very prone to dimerisation upon heating to room temperature (o-Xylylene has a high thermal reactivity) or exposure to a XeCl/XeF laser. Two molecules of o-Xylylene could come together in a Diels-Alder cycloaddition as there'd still be a diene and dienophile component. However, this is less feasible as the conjugation around the ring would reduce the reactivity of the dienophile.

The reason why the Diels-Alder cycloadditions, via the terminal diene, and the Cheletropic cycloadditions above are so thermodynamically favourable is due to the aromatization of the 6-membered carbon ring of the products. The products experience significant stabilisation due to the delocalisation of the 6π electrons. This can be seen in the animations above. The product of the Diels-Alder pathway, via the internal diene, is not aromatic, hence the unfavourable thermodynamic nature of this pathway.

Furthermore, as Figure 24 shows, o-Xylylene can undergo an intramolecular Diels-Alder cycloaddition to form benzocyclobutene. This is a competing reaction pathway and will be more prominent in low concentrations of SO₂. This system contains 4π electrons and the orbitals interact antarafacially, as shown in the σ-framework. Hence, this reaction would be thermally allowed, by the Woodward-Hoffmann rules, as there is only one (4r)_a and no (4q+2)_s components. As both orbitals rotate clockwise, it is a conrotatory electrocyclic reaction. This is in line with "All thermal electrocyclic reactions involving (4n)π electron systems, where n is an integer, are conrotatory". The formation of the aromatic benzocyclobutene product is thermodynamically favourable, as shown in the table below.

	Activation energy (Ea) (kJ/mol)	Reaction energy (ΔGr) (kJ/mol)
Intramolecular Diels-Alder cycloaddition of o-Xylylene	+144.14	-52.93

(Similar to this section Tam10 (talk) 15:11, 6 December 2016 (UTC))