Rep:Mod:KSG115
Krishan Gosai Molecular Modelling 2
Using Gaussview, I optimised various molecules to find out key information such as energy and charge density. The energies associated with N2, H2 and NH3 were used to calculate the energy change in the Haber-Bosch process of ammonia production.I then focused on one molecule of S2 and this led me to important details of the molecular orbitals it consists of and the vibrational modes.
NH3 Molecule
Optimisation Properties
| Property | Value |
|---|---|
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy E(RB3LYP) | -56.55776873 a.u. |
| RMS Gradient | 0.00000176 a.u. |
| Point Group | C3V |
| Bond Length | 1.01797 A |
| Bond Angle (H-N-H) | 105.746 degrees |
Item Value Threshold Converged? Maximum Force 0.000003 0.000450 YES RMS Force 0.000002 0.000300 YES Maximum Displacement 0.000028 0.001800 YES RMS Displacement 0.000017 0.001200 YES
Jmol 3D molecule
Ammonia molecule |
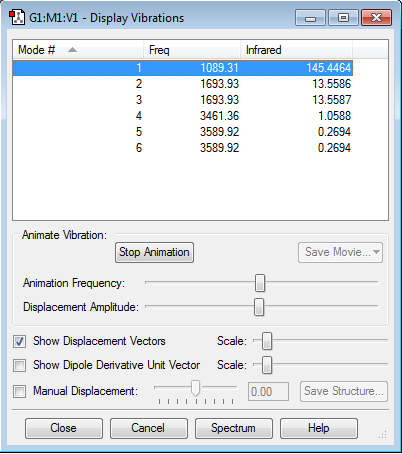
Display Vibrations
How many modes do you expect from the 3N-6 rule?
With there being 4 atoms, the rule would give 6 modes of vibration.
Which modes are degenerate (ie have the same energy)?
Modes 2 and 3 have the same energies and modes 5 and 6 also have the same energies. Each pair are therefore degenerate.
Which modes are "bending" vibrations and which are "bond stretch" vibrations?
Modes 1,2 and 3 are bending vibrations.Modes 4,5 and 6 are all bond stretching.
Which mode is highly symmetric?
4, the symmetric stretch.
One mode is known as the "umbrella" mode, which one is this?
1
How many bands would you expect to see in an experimental spectrum of gaseous ammonia?
Two bands would appear. This is because only three vibrational modes (1,2 and 3) cause a change in dipole and two of these modes (2 and 3) are degenerate. The bands would occur at frequencies of 1089.31 and 1693.93 respectively.
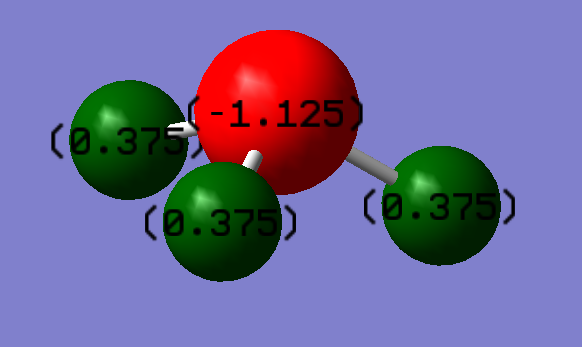
Charge Density
I would expect a much more negative charge on the nitrogen atom compared to the three hydrogen atoms due to it being much more electronegative and its lone pair. The charge on the nitrogen is -1.125 and the charges on the hydrogens are 0.375 respectively.
N2 Molecule
Optimisation Properties
| Property | Value |
|---|---|
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy E(RB3LYP) | -109.52412868 a.u. |
| RMS Gradient | 0.00000060 a.u. |
| Point Group | D∞h |
| Bond Length | 1.10550 Angstroms |
| Bond Angle | N/A Linear Molecule |
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Jmol 3D Molecule
Nitrogen molecule |
Display Vibrations
For linear molecules there is a 3N-5 rule. Since there are only two atoms, this would result in there being only one mode of vibration, which is shown. This mode of vibration is a stretch. There is no infrared data as there is no change in dipole, which is required for a molecule to be found on an IR spectra.
Charge Density
Since both atoms are homogenous, there is no difference in charge. The both possess the same electronegativity so they withdraw electron density equally to an equilibrium, resulting in neutral charges.
H2 Molecule
Optimisation Properties
| Property | Value |
|---|---|
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy E(RB3LYP) | -1.17853936 a.u. |
| RMS Gradient | 0.00000017 a.u. |
| Point Group | D∞h |
| Bond Length | 0.74279 Angstroms |
| Bond Angle | N/A Linear Molecule |
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
Jmol 3D Molecule
Hydrogen molecule |
Display Vibrations
For linear molecules there is a 3N-5 rule. Since there are only two atoms, this would result in there being only one mode of vibration, which is shown. This mode of vibration is a stretch. There is no infrared data as there is no change in dipole, which is required for a molecule to be found on an IR spectra.
Charge Density
Since both atoms are homogenous, there is no difference in charge. The both possess the same electronegativity so they withdraw electron density equally to an equilibrium, resulting in neutral charges.
Ammonia Production
E(NH3)= -148492.421801 kJ/mol
2*E(NH3)= -296984.843601 kJ/mol
E(N2)= -287555.599849 kJ/mol
E(H2)= -3094.25508968 kJ/mol
3*E(H2)= -9282.76526904 kJ/mol
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -146.47848396 kJ/mol
The gaseous reactants are more stable than the ammonia product as the energies associated with them are lower than the product.
Literature values state that the enthalpy change for one mole of the Haber process is around -46 kJ/mol [1]
- ↑ G. Ertl: Surface Science and Catalysis: ”Studies on the Mechanism of Ammonia Synthesis: The P. H. Emmett Award Address. In: Catalysis Reviews. 21, 1980, S. 201–223.
so for two moles of ammonia it would be -92 kJ/mol. Above I have calculated the energy change for two moles of ammonia as well. When a reaction is occurring at constant pressure and volume, energy change = enthalpy change (according to the thermodynamic equation of H = E + PV). During the Haber process, volume and energy are both constant. The difference between the literature value and the computer modelling value is 54.47848396 kJ/mol. This value is much lower in energy and a more exothermic reaction. The computer modelling system does not take into account entropy change, which would cause a large variation in energy calculated. It does not take into account interactions between nitrogen, hydrogen and ammonia molecules, which although may be small in the gas stage, can have some effect on the calculations.
S2 Molecule
Optimisation Properties
| Property | Value |
|---|---|
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy E(RB3LYP) | -796.32599779 a.u. |
| RMS Gradient | 0.00000372 a.u. |
| Point Group | D∞h |
| Bond Length | 1.92943 Angstroms |
| Bond Angle | N/A Linear Molecule |
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000011 0.001800 YES RMS Displacement 0.000016 0.001200 YES
Jmol 3D Molecule
Disufur molecule |
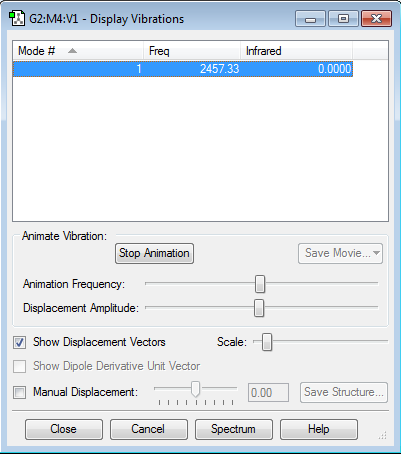
Display Vibrations
There is only one type of vibration available for a linear molecule, which is a symmetric stretch. The frequency for this stretch is low and would not be found on an IR spectra as there is no change in dipole. The positive value for frequency shows that there as been a successful optimisation of the molecule. For linear molecules there is a 3N-5 rule. Since there are only two atoms, this would result in there being only one mode of vibration, which is shown.
Charge Density
Since both atoms are homogenous, there is no difference in charge. The both possess the same electronegativity so they withdraw electron density equally to an equilibrium, resulting in neutral charges.
Molecular Orbitals
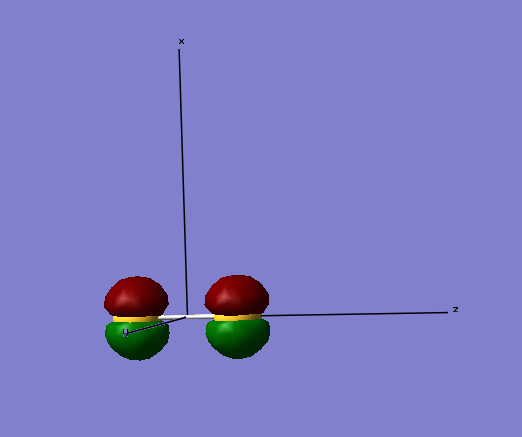
Molecular Orbitals made from 2s atomic orbitals
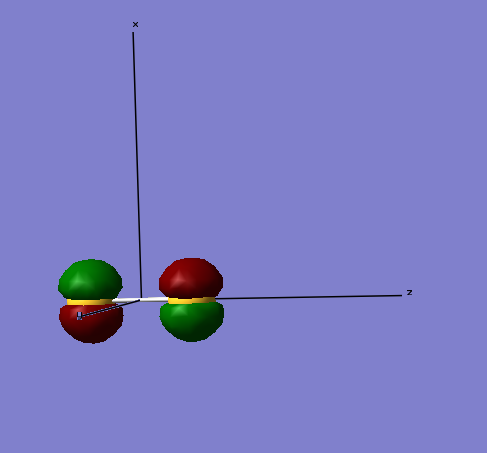
The above image shows the molecular orbitals of a sigma-bond in its bonding phase. The electrons for the orbital come from the 2s (along the z-axis) orbitals from both S atoms. The below image is of the anti-bonding sigma molecular orbital, which is also made from the 2s orbital electrons. As you can see, the atomic orbitals are in different phases, making them anti-bonding. As the anti-bonding orbital is filled with two electrons, the sigma-bond becomes dissociated. Although not shown, the molecular orbitals formed from the 1sz possess the lowest energies associated with them, with the bonding molecular orbital being -88.93663 a.u. The electrons involved in making this molecular orbital are core electrons, not valence electrons, so have a much lower energy associated to them.
The bonding molecular orbitals formed from the 2sx atomic orbitals possess and energy of -7.99779 a.u. and the anti-bonding orbital having an energy of -7.99769 a.u., respectively. These values are substantially greater than energies associated with the molecular orbitals formed from the 1s atomic orbitals.
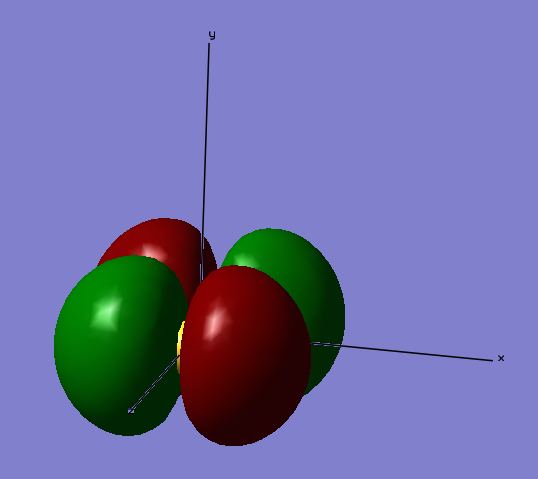
Pi-bonds formed from 2p atomic orbitals
The first image shows the molecular orbital of a pi-bond. This has formed with electrons from the 2px atomic orbitals. The image below shows the anti-bonding pi-bond. It is anti-bonding as the atomic orbitals are in different phases. Both the bonding and anti-bonding molecular orbitals formed from the 2px atomic orbitals have energies of -5.96349 a.u.
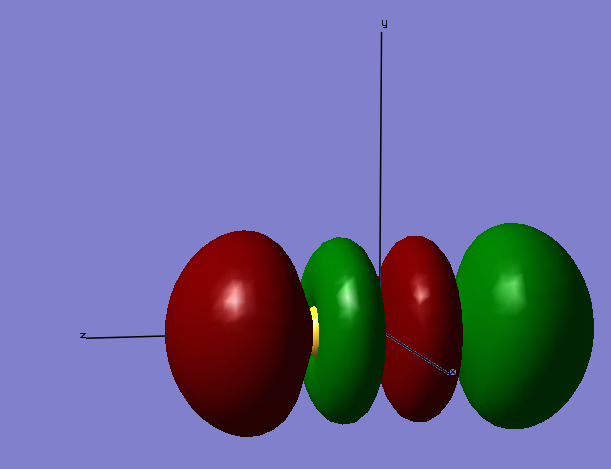
Molecular orbitals formed from 3s and 3p atomic orbitals
The image below shows a bonding molecular orbital formed with electrons from the 3sz atomic orbitals. The overlap between the two atomic orbitals is so strong that the bonding orbital looks like one whole surface. This is because they include valence electrons and so are more involved in bonding. Due to the bonding molecular orbital being made from valence electrons, the energy associated with the orbital is much higher than other molecular orbitals made from 2s or 2p atomic orbitals. This bonding molecular orbital has an energy of -0.83212 a.u. associated with it.
The following image is of a pi-bond. This molecular orbital is made from two atomic orbitals, both being from the 3py orbitals. Once again, there seems to be an extended shell of molecular orbital as they are made from valence electrons, leading to more involvement in bonding. The valence electrons lead to the energy associated with the pi bond to be greater than molecular orbitals made from 2s or 2p atomic orbitals. This pi-bond has a energy of -0.34959 a.u. associated with it.
HOMO
The HOMO is an anti-bonding pi-bond molecular orbital made from two 3px atomic orbitals. The molecular orbital only has one lone electron and has an energy of -0.18463 a.u. The HOMO is an anti-bonding orbital as it has atomic orbitals out of phase.
LUMO
The LUMO is an anti-bonding sigma-bond molecular orbital made from two 3p3pz atomic orbitals. There are no electrons occupying the orbital. The LUMO has a higher energy than the HOMO, as it has an energy of -0.01305 a.u.