Rep:Mod:KS5214TSandR
Introduction
How Gaussian and GaussView Work
Gaussian is an electronic structure package capable of predicting many properties of atoms, molecules and reactive systems, for example transition structures, energies and frequencies. It utilizes ab initio methods such as density functional theory, semi-empirical, molecular mechanics, and hybrid. GaussView is a graphical interface for Gaussian 03. It allows to build molecules or reactive systems, setup Gaussian 03 input files and graphically examine results. There are different levels of theory available: semi-empirical (AM1, PM6); density functional theory (B3LYP, MPW1PW91); ab initio (HF, MP2, CCSD). The level of theory is the set of underlying approximations used to describe the chemical system. Higher levels of theory are often more accurate however they come at much greater computational cost. Basis sets are used for most calculations in Gaussian. They are a set of functions that are used to describe electronic wave-functions and can be considered as the building blocks, which are linearly combined to produce the molecular orbital representation for the calculation: Pople-type (3-21G, 6-31G, 6-311G(d,p)); Dunning (cc-pVDZ, aug-cc-pVTZ); Huzinaga and others. The higher the basis set, the more expensive the computational method and the more time consuming, as more elements are taken into account to construct the molecular orbital representation.
GaussView provides the advantage of drawing structures and optimising them instead of typing all the coordinates, theory, basis sets as code in Gaussian. GaussView generates the Gaussian input file, and can run Gaussian without ever returning to the unix prompt. GaussView can also be used to read Gaussian output files, visualising the results, making analysis and interpretation much easier.
In this experiment two methods were used, the semi-empirical and the density functional theory, in order to investigate transition states and reactivity of different Diels-Alder reactions. The semi-empirical quantum chemistry methods are based on the Hartree–Fock formalism, but make approximations and obtain parameters using experimentally acquired data, making the computational predictions comparable to empirical data. These methods are usually referred to through acronyms encoding some of the underlying theoretical assumptions. The most frequently used methods (PM6, AM1) are based on the Neglect of Differential Diatomic Overlap (NDDO) integral approximation. The basis sets used in semiempirical calculations are optimized minimal basis sets composed of Slater-type orbitals. Only valence electrons are considered, thus the core electrons are treated together with the nuclei as one effective core potential.
The density functional theory (DFT) is presently the most successful and promising approach to compute electronic structures. I can be used for a range of calculations from atoms, molecules and solids to nuclei and quantum and classical fluids, predicting a variety of molecular properties including molecular structures, vibrational frequencies, atomisation energies, ionisation energies, electric and magnetic properties, and more. [1][2]
Potential Energy Surfaces and Transition States
Chemical reactions can be simulated relative to internuclear distance and momentum of atoms, in order to observe the relative positions of the atoms during a reaction using potential energy surfaces. The internuclear distance of the reactants versus products as well as the potential energy are all presented on the same trajectory allowing conclusions to be made regarding the transition state of a specific reaction path. A reactive trajectory moves from reactants to products, passing through the transition structure shown as a saddle on the plot. An unreactive trajectory bounce off and the reactants are regenerated.
Potential energy trajectories relate the potential energy with the relative positions of the species taking part in the reaction. The path followed is observed by a black line, which when straight indicates no vibrational energy present in bond, whilst when it oscillates it indicates vibrational energy, and its relative position on the trajectory provides information about the position of the atoms.
Figure 1. An example of Potential Energy against Bond Distance Trajectory
The reaction path goes through a saddle point, which is a maximum at the potential energy curve, and it indicates a transition state for the reaction. The relative position of the saddle point depends on the amount of vibrational and translational energy present in the species reacting. Both the minimum and the transition state have a gradient of zero, as they are both stationary points. Mathematically, minima and transition states differ in that although both are stationary points a minimum is a minimum in all directions, but a transition state is a maximum along the reaction coordinate and a minimum in all other variables.
Nf710 (talk) 14:17, 30 December 2016 (UTC) its is the curvature in all directions! mathematically this is the second derivative.
Diels-Alder Reactions
Pericyclic reactions make an important body of chemical reactions and are thus extensively studied. The four principle classes of pericyclic reactions are termed: Cycloaddition, Electrocyclic, Sigmatropic, and Ene Reactions.
The most common cycloaddition reaction is the [4π+2π] cyclization known as the Diels-Alder reaction. This reaction has a great synthetic importance and was discovered by the German chemists, Otto Diels and Kurt Alder, who received a Nobel Prize in 1950. The driving force of the famous Diels-Alder reaction in the formation of two new σ-bonds, which are energetically more stable and thus favourable, than the π-bonds being broken.[3]
The Diels-Alder reaction is a thermal cycloaddition whose mechanism involves the σ-overlap of the π-orbitals of the two unsaturated systems. There is not a single mechanism for all Diels-Alder reactions. At first approximation, we can divide them into two classes :
- Synchronous and symmetrical, concerted mechanisms - when the two new bonds are formed simultaneously. In the transition state, the two forming bonds have the same lengths.
- Multistage, non-concerted and asynchronous mechanisms. The transition state is a di-radical, with one bond being formed first.
There are two different ways in which the Diels-Alder Cycloaddition can be set up:
- normal and
- inverse electron demand
In the normal electron demand the dienophile contains an electron withdrawing group, which makes the LUMO (lowest unoccupied molecular orbital) lower in energy; whilst the diene contains electron donating groups, which makes the HOMO (highest occupied molecular orbital) rise in energy. This therefore reduces the energy gap between the HOMOdiene and the LUMOdieneophile and therefore there is better overlap of orbitals, resulting in stronger interactions. The inverse electron demand, is when the dienophile contains the electron donating groups; which makes the HOMO rise in energy. The diene will contain the electron withdrawing groups, reducing the energy of its LUMO but giving the same result- the interacting orbitals are closer in energy and interact stronger.[4][5]
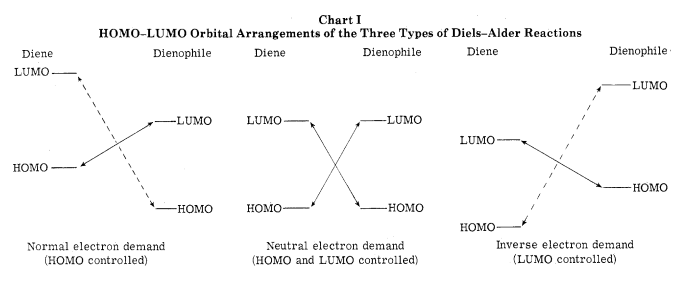
Figure 2. HOMO-LUMO Interactions of Different Diels-Alder Reactions (from J. Org. Chem., 40, No. 8, 1975 p. 1112)
The Experimental
At this lab, three ways of optimising and calculating transition states of reactions were studied:
- Optimising the transition state directly, which is the fastest method, yet it is quite unreliable and cannot be used when the transition state structure is not known.
- Generating a guess transition structure and freezing bond coordinates of the reacting atom, which provides reliable results in a fast way. However it still cannot be used if the transition state structure is not known.
- Starting from the optimisation of products, and deleting bonds, altering bond lengths, in order to get the transition state structure. This is the most reliable of the three methods, but requires the most steps and time. It can be used even if the TS is not known.
In this experiments the transition state was located using one of the three methods, and was confirmed by running an intrinsic reaction coordinate (IRC) calculation. The IRC can be used to follow the minimum energy reaction path from a transition structure down to its local minimum. In order to prove that the desired transition state was obtained from the optimisation, one must follow the reaction path from the transition state down in energy in both directions. The reason for this is that there may be different reaction pathways, via different transition states, yielding the same product. The reaction path is the one with the steepest descent path from the transition state to the product. Molecular orbital analysis and thermochemical analysis was then performed in order to investigate the Diels-Alder setup (normal or inverse electron demand) and the reaction type (concerted or multistage).
Nf710 (talk) 14:21, 30 December 2016 (UTC) Very good intro, however it would have been slightly better if you could have shown some understanding of the levels of theory
Exercise 1: Reaction of Butadiene with Ethylene
Conjugated dienes such as butadiene 1 undergo cycloaddition reactions with multiple bonds (dienophiles) to form unsaturated six-membered rings. In conventional cycloaddition reaction terminology, this is a [4+2]–cycloaddition reaction involving 4 π-electrons of the diene and 2 π-electrons from the dienophile, in this case ethylene 2.
In this exercise, we look at a basic diels alder reaction where there are no substituents on the dieneophile and the diene. The reaction would not occur at room temperature due to a large energy gap between the HOMOs and the LUMOs of the two reactants.
In these calculations, the two fragments 1 and 2 were optimised with the semi-empirical method using the parameterization method 6 (PM6) of the Hamiltonian. [6] The semi-empirical quantum chemistry methods are based on the Hartree–Fock formalism, but make approximations and obtain parameters using experimentally acquired data, making the computational predictions comparable to empirical data. The optimised fragments were used to optimise the transition state, also at the PM6 level, using the redundant coordinate editor to freeze the carbons reacting to form the two new σ-bonds. The acquisition of the transition state was confirmed by running an IRC. A transition states is always a first-order saddle point in the energy map - energy rises in all directions but one. If energy would have lowered in two directions or more, then it is obvious that there would be an other path between reactants and products where every point is lower energy than this one. The product, cyclohexene 3 was also optimised using the same basis set.
Optimisation of Fragments
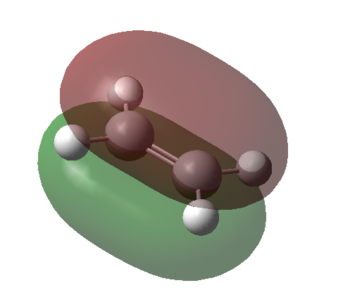
S-cis-butadiene was drawn, and the dihedral angle was changed to 0.00°, allowing the molecule to adopt C2v point group symmetry.The Optimisation log file can be found here. From the images it can be seen that the LUMO is a symmetric molecular orbital, whereas the HOMO is anti-symmetric with respect to the yz-plane.
|
|
|---|---|
| Figure 3. HOMO of Butadiene | Figure 4. LUMO of Butadiene |
Ethylene was also drawn and optimised using the PM6 method. Unlike s-cis-butadiene, the HOMO is symmetric and the LUMO is anti-symmetric. The Optimisation log file can be found here.
|
|
|---|---|
| Figure 5. HOMO of Ethylene | Figure 6. LUMO of Ethylene |
Optimising the Transition State
The 'structure' was drawn from the two fragments above, and was symmetrised to the Cs point-group and then optimised. It was optimised to a transition structure (TS Berny) with the previously mentioned PM6 semi-empirical method.
The Optimisation log file can be found here and IRC here
It can be confirmed that a transition state was found due to the presence of an imaginary frequency at -724.73 cm-1.
The results from these calculations were used to analyse this simple thermal Diels-Alder reaction. Molecular orbital theory and frontier orbitals was used to predict which orbitals will react, and these were compared to the data obtained by the optimization of the product.
Molecular Orbital Analysis
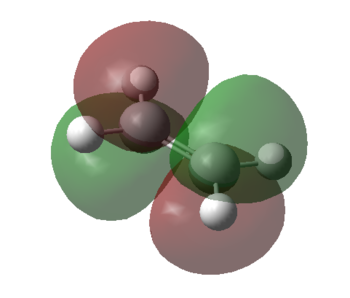
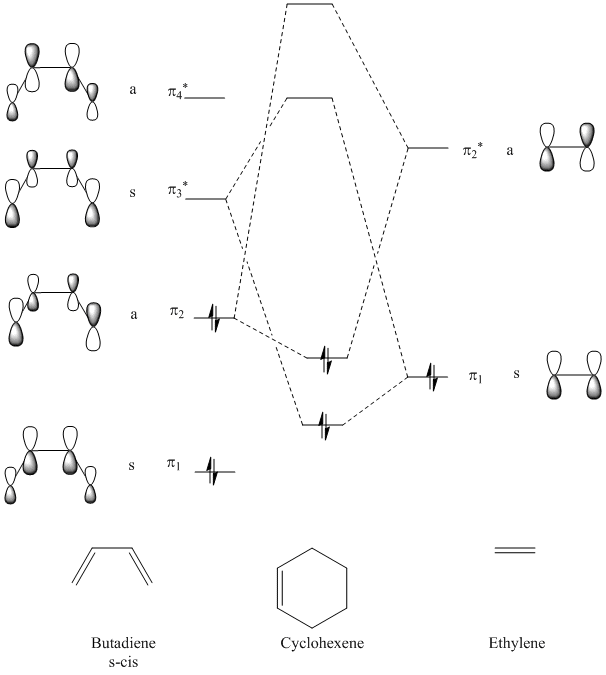
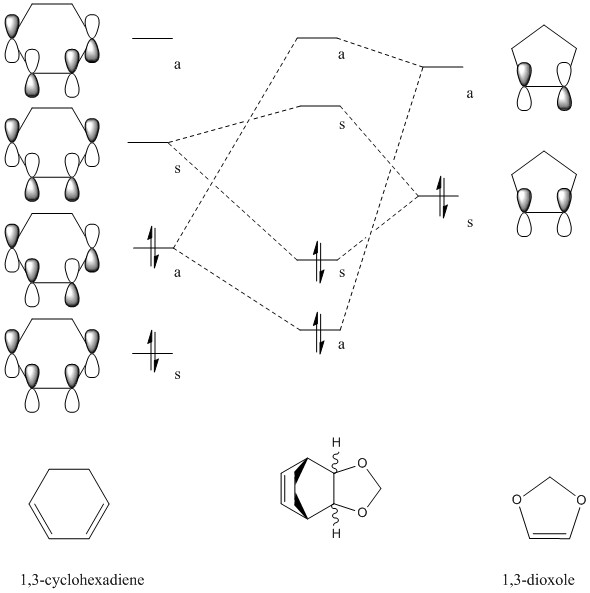
Theoretical, qualitative molecular orbital analysis was performed for 1 and 2 to get Figure 8. Following MO theory, four atomic orbitals (AOs) give four molecular orbitals (MOs), only orbitals that have the same symmetry and are close in energy interact and thus symmetry needs to be preserved. This means that symmetric-symmetric interactions are allowed, as well as anti-symmetric-anti-symmetric, however symmetric-anti-symmetric interactions are forbidden. If the two overlapping orbitals are of different symmetries (AS or SA) then any constructive overlap of the orbitals is counterbalanced by an equal amount of destructive overlap and the net interaction is exactly zero. If the symmetry of the two interacting orbitals is the same (AA or SS) then the integral is non zero and thus it is expected to get constructive overlap. Hence, here as seen by Figure 8. there are two possibilities: the SS and the AA reaction, both of which react suprafacially and conserve symmetry.
Figure 8. MO analysis
It can be seen that the HOMO of the dienophile, 2 is lower in energy than the HOMO of the diene, 1 and therefore it can be concluded that the reaction follows a normal electron demand. This means that the HOMO of ethyleneand the LUMO of s-cis-butadiene combine to form the LUMO of the transition state. Equally the LUMO of ethylene and HOMO of s-cis-butadiene combine to form the anti-symmetric HOMO of the transition state.
The theoretical, qualitative MO constructed above can be compared with the computed molecular orbitals from the calculations.
Intrinsic Reaction Coordinate and Mechanism of Reaction
As aforementioned, the IRC is used to confirm that the correct transition state has been optimised. It can be confirmed that a transition state was found due to the presence of an imaginary frequency at -724.73 cm-1:
The IRC movie shows that the bonds break and form in a concerted fashion whilst the plotted IRC path shows that only one transition state is present during the cycloaddition which is shown by only one peak on the path. The transition structure is the structure with the highest energy on the IRC path. From this diagram it can also be seen that the transition state is very close in energy to the reactants, which makes it an early transition state according to Hammond's Postulate.
|
|
|---|---|
| Graph 1. Total Energy along IRC of Diels-Alder Cycloaddition | Clip 2. Bond Forming Process - Concerted |
Furthermore the lowest positive/real vibrational frequency will be shown. The lowest real vibrational frequency was calculated to be at 108.33 cm-1. This corresponds to an asynchronous vibration/wag of the transition structure.
Clip 3. Lowest Energy Real Frequency
Bond Measurement Analysis
During this reaction the three π C-C double bonds between C1-C4, C9-C14 and C11-C7 are breaking and new σ C-C single bonds are formed between C4-C14 and C7-C11. The distance between the carbons for which a single bond is formed is around 2.02 Å. The Van-der-Waal's radius for one carbon atom is 1.7 Å, which means that the distance between two carbons which are not interacting should at least be equal to 3.4 Å. The distance present is much smaller than that expected and it can therefore be said that during the transition state electronic interaction between these carbons are already present. However, it is also known that an average C-C bond length for sp³ hybridised carbons is around 1.52 Å. The distance found in the transition state is larger than that, so it can be concluded the bond has not yet formed. The typical bond length for sp² hybridised C-C double bonds is 1.34 Å. The bond length found between the carbons previously bound via a single bond is slightly larger than that, meaning that the bond is beginning to break. At the same time it is forming between C1-C3 where the bond length is also slightly larger, which is indicative for a concerted mechanism.[7]
| C1-C4/Å | C9-C14/Å | C7-C11/Å | C7-C9/Å | C4-C14/Å | C1-C11/Å |
|---|---|---|---|---|---|
| 1.444 | 1.436 | 1.438 | 1.361 | 2.033 | 2.018 |
Table 1."Bond" Lengths in Transition State/Å
Figure 9. Labeled Atoms in Transition State
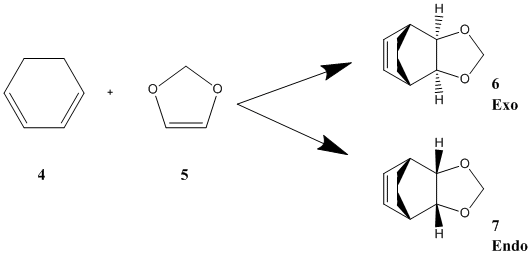
Exercise 2: Reaction of 1,3-Cyclohexadiene and 1,3-Dioxole
Diels-Alder reactions are stereospecific depending on the substituents on the dienophile and the diene, as addition is concerted and happens syn on both components. Cyclic starting material however restrict the structure, due to the ring systems, and there are two possible products that obey the Woodward Hoffmann rules. Despite having four stereogenic centers, 6 and 7 are the only possible diasteromers as any other diasteromer would be very strained. The two hydrogens must therefore be cis in the product, allowing only two compounds to be possible, the exo and the endo products. The product formed depends on the alignment of the diene and dieneophile in the transition state. When the dienophile and the diene are aligned directly on top of each other the endo product is achieved, whilst when a staggered arrangement is undertaken by the two reactants exo is achieved. The endo transition state is thought to be stabilised by interactions between the oxygen atoms and the back of the diene that are attributed to orbital, dipolar and van der Waals interactions. [6] In the case of 1,3-cyclohexadiene and 1,3-dioxole, having an excess of 5 would result in predominantly the endo product, whilst having an excess of 4 would result in predominantly the exo product, when the reaction takes place via a radical cation mechanism using ketone-LiClO4 mixtures. [8]
Scheme 2. Diels-Alder of 1,3-Cyclohexadiene and 1,3-Dioxole
In this exercise, computational calculations were carried out using method 3 from the tutorial, starting with an optimisation of the product using method PM6. The new σ bonds were deleted after optimisation, and the fragments were moved at a distance of 2.05 Å apart. The bonding atoms were frozen, and the fragments were reoptimised before a transition state was calculated with the PM6 method. The IRC was also deduced using the PM6 method to ensure that the correct transition state was reached. From the transition state at a PM6 level was re-optimised at the B3LYP/6-31G(d) level. This was carried out for both the endo and the exo reactions.
Additionally, frequency calculations were carried out for 1,3-cyclohexadiene , 1,3-dioxole, as well as for the endo and exo products to ensure that there were no imaginary frequencies in the starting material or the products.
Molecular Orbital Analysis
Drawing a qualitative molecular orbital diagram (Figure 10) it can be deduced that the the HOMO of the diene 4 and the LUMO of the dienenophile 5 are anti-symmetric, whilst the LUMO of the diene 4 and the HOMO of the dieneophile 5 are symmetric. This is also observed in the optimised MO diagrams from GaussView shown in Figures 11-14 below. The reaction follows inverse electron demand, as the HOMO of the diene is lower in energy than the HOMO of the dienophile. The dieneophile, 5 is electron rich, whilst the diene, 4 is electron poor which is the inverse of a normal Diels-Alder reaction, hence it is called Inverse Electron Demand. The LUMO of the diene, and the HOMO of the dienophile (both symmetric) are now closer in energy and thus there is stronger orbital interaction. However the lowest energy molecular orbital is an anti-symmetric one, between the HOMO of the diene and the LUMO of the dienophile due to the competing energy difference (distance) between the fragment orbitals. [9][10][11]
Figure 10. Qualitative Molecular Orbital diagram of DA reaction between 1,3-cyclohexadiene and 1,3-dioxole
 |
 |
 |
 |
|---|---|---|---|
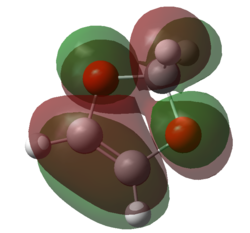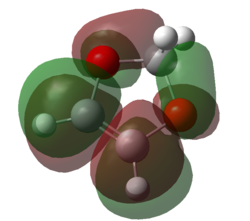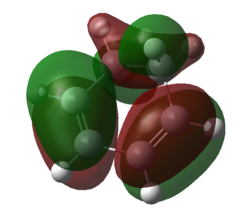| Figure 11. HOMO of 1,3-dioxole | Figure 12. LUMO of 1,3-dioxole | Figure 13. HOMO of 1,3-dioxole | Figure 14. LUMO of 1,3-dioxole |
Taking a close look at the molecular orbitals of the transition state, it is clear that the explanation above holds correct. The lowest energy of the four frontier MOs is an anti-symmetric MO even though 1,3-cyclohexadiene is the electron poor molecule in the reaction and 1,3-dioxole is electron rich, which shows that even though the LUMO of the diene and the HOMO of the dienophile are closer in energy and interact more strongly, energy difference between fragment orbitals is a strongly competing effect.
Intrinsic Reaction Coordinate and Mechanism of Reaction
As seen in exercise 1, the IRC is used to confirm that the correct transition state has been optimised. It can be confirmed that a transition state was found due to the presence of an imaginary frequency at -520.94 cm-1 for endo and at -528.96 cm-1 for exo:
|
|
|---|---|
| Clip 4. Imaginary Freq of endo transition state | Clip 5. Imaginary Freq of exo transition state |
The IRC movie for the endo and exo reactions show that the bonds break and form in a concerted fashion whilst the plotted IRC paths show that only one transition state is present for each reaction mechanism during the DA cycloaddition.
|
|
|---|---|
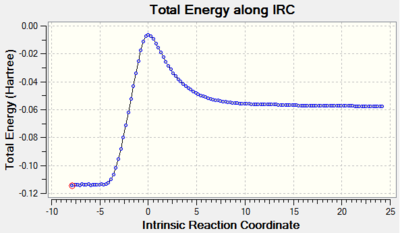
| Graph 2. Total Energy along IRC of endo reaction (N.B. Graph is reversed - products on the left) | Clip 6. Bond Forming Process for endo Product- Concerted |
|
|
|---|---|
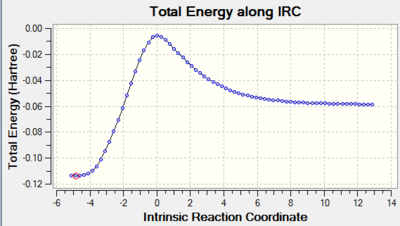
| Graph 3. Total Energy along IRC of exo reaction (N.B. Graph is reversed - products on the left) | Clip 7. Bond Forming Process for exo Product- Concerted |
Thermodynamic and Kinetic Analysis of Reactions
The electronic and zero-point energies are calculated at 0K, whereas the the electronic and thermal energies are calculated at 298.150 K and 1.000 atm. At 298.150 K and 1.000 atm the energy is slightly different due to the existence of vibrational, rotational and translational energy contributions, altering it from the frozen structure at 0 K. The thermal enthalpy is calculated using:
where H=Thermal Enthalpy, E=Thermal Energy, R=Ideal Gas Constant and T=Temperature in Kelvin, assuming constant pressure.
For the zero point energy the enthalpy would be equal; since at 0 K, RT term would be 0. However, at 298.150 K this term becomes significant and therefore the thermal enthalpy is slightly higher, which satisfies the equation. The sum of electronic and thermal free energies however differs in the sense that the entropic contribution becomes significant. Talking about free energies the following equation needs to be used:
Since T= 298.150 K the TS term becomes large and positive and therefore the thermal free energy term is smaller than the other terms. In order to use the equation G=H-TS one needs to know the entropy of the system, which is determined using the partition function.[12]
To calculate the free energy difference of the reactants and products, as well as of the reactants and transitions states, the following method was used. The reactant and product structures of the endo and exo reactions were copied from the appropriate IRC file ( log file for endo IRC , log file for exo IRC ) and frequency analysis was carried out for each of the reactants/products using the Density Functional Theory (DFT) method and the and 6-31G(d) basis set. The thermodynamic data obtained from the log file of the endo product are summarized in Table 2 and for the reactants of the endo reactions, obtained from the starting material log file are summarised in Table 3. The data obtained for the transition state also at the 6-31G(d) level are also summarized, in Table 4 in order to deduce the activation energy of the endo reaction.
|
|
| |||||||||||||||||||||||||||||||||||||||||||||
| Table 2. Thermodynamic Properties of endo product | Table 3. Thermodynamic Properties of endo starting materials | Table 4. Thermodynamic Properties of endo transition state |
The difference in the sum of electronic and thermal free energies of the products and the sum of the electronic thermal and free energies of the reactants was calculated giving a value of: 0.043285 a.u. which equals to 113.645 kJ/mol. This represents the thermodynamic stability of the reactants compared to the starting material. The difference between the electronic and thermal free energies of the transition state and the reactants was also calculate in order to find the activation energy of the reaction which is equal to 0.039393 a.u. which is equal to 103.426 kJ/mol.
The same was repeated for the exo product using the log files of the frequency analysis for the products and the reactants (structures taken from the IRC file and the log file of the transition state all at the DFT, 6-31G(d) level:
|
|
| |||||||||||||||||||||||||||||||||||||||||||||
| Table 5. Thermodynamic Properties of exo product | Table 6. Thermodynamic Properties of exo starting materials | Table 7. Thermodynamic Properties of exo transition state |
The thermodynamic stability of the reactants according to the products was calculated in the same manner as above giving 0.044215 a.u. which equals to 116.086 kJ/mol, and the activation energy is 0.040346 a.u. which is equal to 105.928 kJ/mol.
As expected, the exo reaction gives the thermodynamic product, which is shown by the higher stabilization energy for the reactants, 116.086 kJ/mol in comparison to that of the endo reaction being 113.645 kJ/mol. The exo reaction forms a less strained product as the hydrogen point in the opposite direction to the bridgehead. However, the endo reaction gives the kinetic product as the activation energy to the transition state is lower in the endo (103.426 kj/mol) than the exo (105.928 kJ/mol). The reason for this is the stabilization of the oxygens with the back of the diene, as mentioned above.
An alternative way to carry these calculations out are to take the frequency files for the starting material and products from the optimised structures (not the IRC) at infinite distances apart.
Other Significant Interactions and Comments
As aforementioned, the endo reaction is favored by interactions between the electron density of the oxygen atoms and the back of the diene. This is clearly illustrated in Figure 15, where the blue orbitals of the oxygens, is clearly overlapped with the orbitals of the back of the diene. This interaction stabilises the transition state of the end product, lowering the activation energy and therefore allowing the reaction to proceed with greater ease compared to the exo. The exo configuration lacks this favoring interactions between the orbitals as the two molecules are staggered. The lack of the interaction results, as seen above, to higher activation energy for the exo product. However, in the product, the exo arrangement is more favorable and it is thus the thermodynamic product.
| Figure 15. HOMO of endo TS | Figure 16. HOMO of exo TS |
14:44, 30 December 2016 (UTC) The layout of these tables is extremely unhelpful. A table of just the reaction energies and activation energies would have been fine. you have however shown good understanding in this section. But you have got the wrong answer for the reaction energies. Overall still a good section.
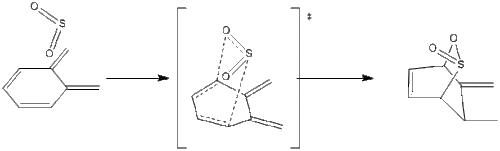
Exercise 3: Diels-Alder vs Cheletropic
The reaction of O-xylylene, 8 and sulfur dioxide, 9 can yield to two possible products following a hetero Diels-Alder cycloaddition reaction yielding a sultine analog, 11 or a cheletropic reaction yielding a sulfolene analog, 10.
Scheme 3. Reaction of O-xylylene with SO2
Diels-Alder reactions, as seen above, can be exo or endo depending on the arrangement of the dienophile 9 relative to the diene 8. When considering the Diels-Alder reaction, one could also argue that there are two possible diene-reaction points: one within the ring (Schemes 4-5), and one outside the ring structure (Schemes 6-7). In this exercise computational calculations were carried out to explain and visualize the reaction between O-xylylene and SO2 and discuss the competing factors between the hetero-Diels-Alder and the cheletropic addition, Scheme 8.
|
|
|
|---|---|---|
| Scheme 4. Endo Reaction with Inner Diene | Scheme 5. Exo Reaction with Inner Diene |
|
|
|
|---|---|---|
| Scheme 6. Endo Reaction with Outer Diene | Scheme 7. Exo Reaction with Outer Diene |
Molecular Orbital Analysis
Before molecular orbital analysis takes place, one must consider the orientation of the molecules during the reaction, as this determines the symmetry of the orbitals involved.
Diels Alder Reactions
 |
 |
 |
 |
|---|---|---|---|
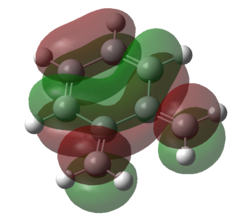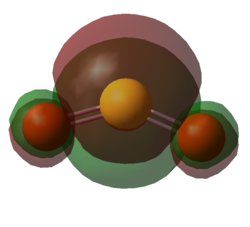
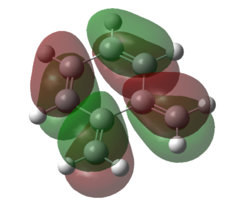
| Figure 17. HOMO of SO2 | Figure 18. LUMO of SO2 | Figure 19. HOMO of O-xylylene | Figure 20. LUMO of O-xylylene |
Taking a look at the orbitals of the starting materials 8 and 9, the HOMO of SO2 and the LUMO of O-xylylene are both symmetric, thus they are expected to interact. This can be seen by the HOMO of the transition state of the endo Diels-Alder reaction, Figure 21, whilst the LUMO of the transition state, clearly shows that it is formed by the interaction of the anti-symmetric fragment orbitals of the reactants.
 |
 |
|---|---|
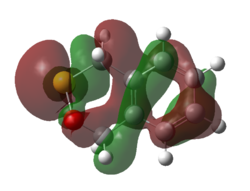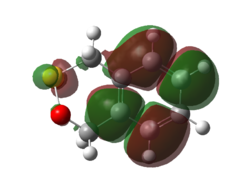| Figure 21. HOMO of Endo Diels-Alder Transition State | Figure 22. LUMO of Endo Diels-Alder Transition State |
(This looks like the product Tam10 (talk) 14:38, 13 December 2016 (UTC))
Cheletropic Addition
Taking into account the orientation with which SO2 approaches the diene (SO2 is perpendicular compared to the planar diene), it is clear that in this case the LUMO of SO2 is anti-symmetric with respect to the plane of the molecule, and interacts with the anti-symmetric HOMO of O-xylylene. Looking at the HOMO and LUMO of the transition state, it is clear that the HOMO is an anti-symmetric orbital interaction between the LUMO of SO2 and the HOMO of O-xylylene.
 |
 |
 |
 |
|---|---|---|---|
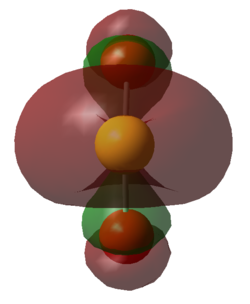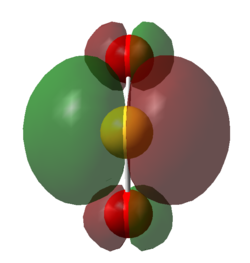
| Figure 23. HOMO of SO2 Down the Plane of the Bonds | Figure 24. LUMO of SO2 Down the Plane of the Bonds | Figure 25. HOMO of TS | Figure 26. LUMO of TS |
Intrinsic Reaction coordinate and Reaction Mechanism
As seen from the IRC files and clips for all of different Diels-Alder reactions: endo (outer), exo (outer), endo (inner) and exo (inner), the reaction happens in a multistage mechanism, rather than concerted as seen in previous examples. However as seen from Clip 12 the cheletropic addition is a concerted reaction.
|
|
|
|
|---|---|---|---|
| Graph 4. IRC Graph of Endo DA Reaction (Outer Diene) | Clip 8. IRC Movie of Endo DA Reaction (Outer Diene) | Graph 5. IRC Graph of Exo DA Reaction (Outer Diene) (N.B. Graph is reversed) |
Clip 9. IRC Movie of Exo DA Reaction (Outer Diene) (N.B. Clip is reversed) |
|
|
|
|
|---|---|---|---|
| Graph 6. IRC Graph of Endo DA Reaction (Inner Diene) | Clip 10. IRC Movie of Endo DA Reaction (Inner Diene) | Graph 7. IRC Graph of Exo DA Reaction (Inner Diene) | Clip 11. IRC Movie of Exo DA Reaction (Inner Diene) |
|
|
|
|---|---|---|
| Graph 8. IRC Graph of Cheletropic Addition | Clip 12. IRC Movie of Cheletropic Addition |
(Interesting IRCs - you've used the local quadratic approximation. Any reason? Tam10 (talk) 14:38, 13 December 2016 (UTC))
Looking at the IRCs closely, it can be seen that the o-xylylene molecule form a transition state that seems to form a four-membered ring where the outer diene is. This is indicated by the dashed lines across the 6-membered ring and the two C=C double donds. This suggests the formation of an intramolecular side product, if SO2 is not close enough to react whilst this transition state is reached.
Figure 27. Possible Intramolecular Side-Product
Thermodynamic Analysis and Reaction Pathways
As observed, theoretically there are 5 different possible reaction pathways. In order to decide which reactions would occur, and what would be the kinetic and thermodynamic product, thermodynamic analysis needs to be conducted in order to find the activation energies of the reactions,giving us the kinetic product with the lowest activation energy, as well as relative reaction energies, with the greatest overall stability in a reaction, giving us the thermodynamic product. These were calculated using the thermochemistry data from the log files of the staring material, the products and the transition states.
Link to Thermodynamic Data Summaries
(Good work adding links to separate pages of data. This makes the report easier to read Tam10 (talk) 14:38, 13 December 2016 (UTC))
Summary of Results
From the thermodynamic data it is clear that only three out of the five possible reactions actually occur. The inner diene does not react and only takes part in the delocalised π-system of the phenyl group. Even though the activation energies are relatively high for the inner-diene DA reaction, the reason this reaction does not occur is the fact that the energy released due to stabilization of products, does not compensate for the energy needed for the reaction to proceed (i.e. the Ea). Even though there is a net stabilization from the reactants to the products, this stabilisation is very small (only 8.56 and 11.33 kJ/mol for the endo and exo respectively) and is thus thermodynamically unfavorable compared to the other net stabilizations of the outer DA and the cheletropic additions which are at a magnitude of a hundred kJ/mol. The activation energies for the reaction with the inner diene are also high compared to the activation energies of the DA with the outer diene or the cheletropic addition which shows that this reaction is both thermodynamically and kinetically unfavorable.
Comparing the two possible Diels-Alder reactions and the cheletropic addition, it is clear that the computational calculations support experimental evidence, that the cheletropic addition is the thermodynamic product whilst the Diels-Alder is the kinetic.[14][15] The cheletropic addition results to greater overall energy stabilization (193.20 kJ/mol) compared to the two possible DA reactions (137.53 and 133.22 kJ/mol for endo and exo respectively). However the DA reaction is the kinetic product, with a preference to the endo as it has the lowest activation energy and thus requires the least amount of energy to form. Out of the two DA reactions, the endo is also the thermodynamic product.
| Reaction | Activation Energy [kJ/mol] | Reaction Energy [kJ/mol] |
|---|---|---|
| Endo DA - Outer | 43.75 | 137.15 |
| Exo DA - Outer | 51.38 | 133.22 |
| Endo DA - Inner | 87.16 | 8.56 |
| Exo DA - Inner | 71.86 | 11.33 |
| Cheletropic Addition | 66.70 | 193.20 |
Table 8. Summary of energies
(It's good practice to add signs to the activation and reaction energies to prevent ambiguity Tam10 (talk) 14:38, 13 December 2016 (UTC))
|
|
|
|---|---|---|
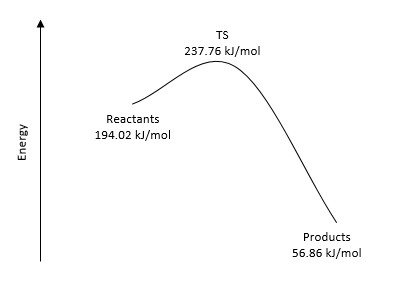
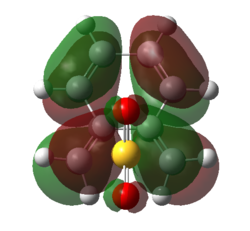
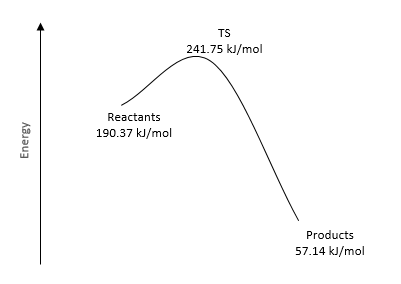
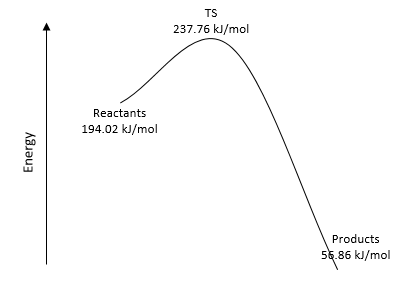
| Figure 28. Energy Reaction Profile for Endo | Figure 29. Energy Reaction Profile for Exo | Figure 30. Energy Reaction Profile for Cheletropic |
Conclusion
In this computational experiments, different Diels-Alder reactions were investigated in terms of their energies, major and minor products, possible side reactions and reaction mechanisms. Starting from simple reactions, with few atoms leading to more complex reactions, different computational methods were used to investigate the transition states and relative reactivity.
For the simplest Diels-Alder reaction between ethylene and butadiene, the transition state was guessed and optimised. Two major problems occur with this computational methods. Firstly the transition state for some of the methods has to be guessed in order to optimise it. This worked here as the systems used are small and thus guessing the transition state is relatively easy. However, this would be a problem when new reactions need to be studied and the transition state is not known. Furthermore only one molecule is considered in the calculations. This neglects intermolecular interactions, because this one molecule is treated like an Ideal Gas.
For the reaction of 1,3-Cyclohexadiene and 1,3-Dioxole it was found that whilst the endo reaction was kinetically more favourable, thermodynamics favoured the exo reaction due to secondary orbital interaction between the oxygens and the back of the diene. The computational results came in agreement with literature results.
The selectivity for the Diels-Alder reaction was also studied for the reaction between o-xylylene and SO2 where it was found that there are two types of reaction possible, a Diels-Alder and a cheletropic addition. For the DA, the endo structure is favoured both thermodynamically and kinetically. Kinetically it is favoured due to a lower activation energy and thermodynamically due to secondary orbital interaction.
Through this experiment it can be seen that computational studies are great when needing to predict the transition state and the reaction mechanism and pathways, as well as to calculate thermodynamic data in order to explain why two molecules react in a specific way. This can be used in order to also investigate the possibility of side reactions in different synthesis projects.
References
[1] Density-Functional Theory of Atoms and Molecules, R.G Parr and W. Yang, Oxford University Press, New York (1989).
[2] A Chemist’s Guide to Density Functional Theory, W. Koch and M.C. Holthausen, WILEYVCH (2001)
[3] McMurry, John. (2004). Organic chemistry. Belmont, CA: Thomson-Brooks/Cole.
[4] J. Org. Chem., Vol. 40, No. 8, 1975 1111-1117
[5] Int. J. Curr. Res. Chem., Pharm. Sci., (2016), 3(5): 40-47
[6] J. Mol. Mod., (2007), 13(12), 1173–1213. DOI: 10.1007/s00894-007-0233-4
[7] New J. Chem., 2016, 40, 6848
[8] Clayden, Jonathan; Greeves, Nick; Warren, Stuart; Wothers, Peter (2001). Organic Chemistry (1st ed.). Oxford University Press. ISBN 978-0-19-850346-0.
[9] J. CHEM. SOC., CHEM. COMMUN., (1985), 1088-1090. DOI: 10.1039/C39850001088
[10] Org. Let. (2008) 10(2): 233-236 DOI:10.1021/ol702614b.
[11] Boger, Dale (1989). Progress in heterocyclic chemistry (1st ed.). New York: Pergamon. ISBN 978-0-08-037044-6.
[12] Acc. Chem. Res. (1968). 1(1): 17–22. DOI:10.1021/ar50001a003.
[13] Joseph W. Ochterski, 'Thermochemistry in Gaussian' www.gaussian.com The offical Gaussian Website. Web. 25.11.2016.
[14] E. Roversi, F. Monnat, P. Vogel, K. Schenk and P. Roversi, Helv. Chim. Acta, 2002, 85, 733–760.
[15] Tetr. Lett. (1994) 35 (27): 4743-4746