Rep:Mod:KRMP
The Cope Rearrangement Tutorial
Optimisation and Frequency Analysis
In this first part of the project, a molecule of 1,5-hexadiene undergoing the Cope rearrangement was studied. The low energy minima and transition states on the potential energy surfaces were located, and this was used to establish the preferred reaction mechanism.
Firstly, a molecule of 1,5-hexadiene was created then rearranged so that the central 4 atoms were in an "anti" relationship to each other. This was then optimised using the HF/3-21G level of theory. The log file relating to this optimisation can be found here. Then a molecule with a "gauche" rearrangement was created and optimised using the same method as the previous molecule. The log file can be found here. The results are summarised below.
| Arrangement | Final energy (au) | Point group |
|---|---|---|
| Anti | -231.68907062 | C2h |
| Gauche | -231.68771610 | C2 |
It would have been expected that the anti-periplanar arrangement would have been lower in energy than the gauche arrangement, due to steric hindrance. However it can be seen that there is little enrrgy difference between them. This is consistent with findings in the literature[1]. The lack of difference suggests that in both arrangements, the favourable orbital overlap interactions between the different sets of orbitals(σC-C-σ*C-H in the "gauche" conformation, σC-C-σ*C-C in the "anti") produce a very similar lowering of energy.
Structure comparison
The two structures (Anti and Gauche) generated are shown below.
I would have guessed that the lowest energy structure would have been the "anti" structure that was previously optimised.
Matching the structures obtained to the structures in Appendix 1 in the script, it can be seen that The gauche structure obtained was gauche 1, and the anti structure was anti 3.
Ci anti 2 1,5-hexadiene
A molecule of 1,5-hexadiene in the anti 2 formation was created and optimised to the HF/3-21G level. The log file can be found here.
The energy of the optimised molecule was -231.69254 au. The energy of the anti 2 molecule in the script was -231.69260. The difference between them is very little as the same molecule was modeled with the same basis set. The molecule was then optimised using a higher basis set (B3LYP/6-31G*) for greater accuracy. The log file can be found here. The final energy was found to be -234.61170 au, which is different to the previous optimisation (by around 1%) and probably closer to the 'true' value. It is not possible however to directly compare energies generated using different basis sets.
Anti 2 Geometry Comparison
The atoms in the molecule of anti 2 1,5-hexadiene optimised to the two different levels were labelled according to the image below.

The geometries of the differently optimised molecules were then compared, and the results tabulated below (all distances were measured in GaussView and given in the unit Å).
| Level of optimisation | Double bond (C1-C2, C5-C6) distance | C2-C3, C4-C5 distance | Central single bond (C3-C4) distance |
|---|---|---|---|
| HF/3-21G | 1.31615 | 1.50887 | 1.55290 |
| B3LYP/6-31G* | 1.33352 | 1.50419 | 1.54814 |
It was seen that the general shape and form of the mole molecules remained generally very similar between the two optimisations. Bond angles within the molecules changed an insignificant amount (<0.3% generally). Bond lengths varied slightly, as shown above. The more optimised molecule had longer C-C double bonds, but slightly shorter single C-C bonds. Also, the molceulce optimised to the B3LYP/6-31G* level had longer C-H bonds throughout.
Frequency Analysis
The anti 2 1,5-hexadiene molecule previously optimised to the B3LYP/6-31G* level was then run through a frequency analysis to verify that the energy level obtained was indeed a minimum. The associated log file for can be found here.
The frequency data below is extracted from the log file, and confirms that the energy at this point is indeed a minimum.
Low frequencies --- -18.6753 -11.7188 -0.0009 -0.0008 -0.0004 1.7893 Low frequencies --- 72.7261 80.1419 120.0206
The various thermochemical energies related to this calculation were then tabulated below.
| Type of energy | Association equation | Value (au) |
|---|---|---|
| Sum of electronic and zero-point energies | E = Eelec + ZPE | 234.469212 |
| Sum of electronic and thermal energies | E = E + Evib + Erot + Etrans | 234.461856 |
| Sum of electronic and thermal enthalpies | H = E + RT | 234.460912 |
| Sum of electronic and thermal free energies | G = H - TS | 234.500821 |
Optimizing the "Chair" and "Boat" Transition Structures
The chair and boat transition structures for the Cope rearrangement consist of two allyl fragments around 2.2Å. One allyl fragment (-CH2CHCH2) was created then optimised to the HF/3-21G level of theory. The log file can be found here and the Jmol can be found below.
test molecule |
Two of these fragments were then taken and arranged into a structure similar to the chair transition state. The ends of the molecules were set to be around 2.2Å apart initially. This arrangement (as pictured below) was then optimised in two different ways.
As with the energy minimum, the transition state occurs when the gradient of the potential energy surface is 0. It is difficult however to locate as at that point the curve has a negative gradient.
The optimisations from here on will use the HF-3-21G level of theory.
Chair transition state optimisation
First Optimisation
The first optimisations attempted used the Opt + Freq calculation aiming for a TS- Berny using the keyword OPT = NoEigen. This keyword stops the calculation fro continuing if more than 1 imaginary frequency is predicted. This may occur if the original guess for the transition state (TS) is not close enough to the 'true' structure. The log file for this calculation can be found here.
One imaginary frequency was found at -818 cm-1 as expected. When animated, this frequency resembles the Cope rearrangement.
Second Optimisation
A second, different optimisation of the original "guess" structure was then tried. This calculation will use the "frozen coordinate" method which can generate a better transition structure and may mean that the Hessian needn't be fully calculated once the molecule is optimised in stages. The log file for the first calculation (freezing the gap between the terminal carbons then optimising the rest of the molecules) can be found here. The frozen carbons were then unfrozen, and the molecules were optimised a second time. This log file can be found here.
The bond making/breaking distances for the 1st optimisation were 2.02038 and 2.02044Å, compared to 2.02049 and 2.02051Å for the 2nd. As can be seen, the actual differences are insignificantly small, suggesting that in fact for this molecule, the 1st, more simple optimisation would have sufficed.
Boat transition state optimisation
The boat transition state will be optimised in a different way to the chair. The method selected was QST2, which specifies the reactant and product and the calculation will find the TS between the two.
The previously optimised anti 2 1,5-hexadiene was specified as both the product and reactant, with the atomic numbering differing between them to inform the calculation what to do. The numbering of each was in accordance with the images below.
An OPT+FREQ calculation was then run using the the HF/3-21G level of theory. This method failed however, (the log file can be found here and produced a chair-like transition state instead of a boat, as in the image below.
.
The calculation cannot find the correct TS, as the possibility of rotation around bonds isn't considered. It is therefore necessary to manipulate the product and reactant molecule to a form closer to the boat TS, as described by the image below.

.
The QTS2 calculation was then run again with the newly manipulated reactant and product molecules. The log file can be found here. The 1 imaginary vibration occured at ≈ 840 cm-1 and was the correct, boat Cope rearrangement TS. The image of which can be found below.
Intrinsic Reaction Coordinate (IRC) Analysis
It is difficult to predict which conformer will result from following the reaction path from each TS. The IRC method allows the user to follow the minimum energy path from the TS to a local minimum on the potential energy surface. This makes a series of points along the path where the slope gradient is greatest.
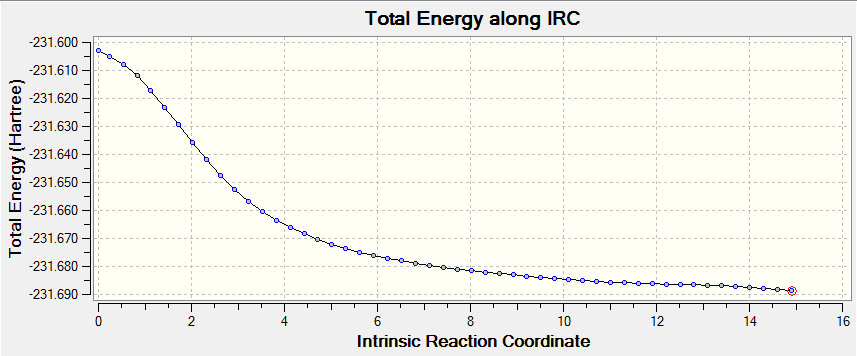
An IRC analysis was run on the previously optimised chair structure, following the forward reaction path and recalculating the force constant every 10 points. The calculation was set to run to 50 points in total. The log file for this calculation can be found here.
From the log file it can be seen that the calculation halted after 39 steps rather than the suggested 50. This is because on the 40th point, it took too many steps to calculate the energy of the structure at the point, and so Gaussian stopped the calculation. The graphed data from the is shown IRC below.


As can be seen from the tabulated data above, the calculation did not reach a zero energy geometry (as the gradient was still non-zero). This means that the calculation needs a further optimisation to find the zero energy structure.
A further optimisation using the HF/3-21G method was then carried out on the structure that had just undergone the IRC analysis to find the minimum point. The log file can be found here.
Looking at the log file, the following section shows a successful convergence at the minimum energy structure.
Item Value Threshold Converged?
Maximum Force 0.000000 0.000015 YES
RMS Force 0.000000 0.000010 YES
Maximum Displacement 0.000055 0.000060 YES
RMS Displacement 0.000017 0.000040 YES
Predicted change in Energy=-8.790074D-12
Optimization completed.
-- Stationary point found.
Carrying out the same IRC analysis but using the optimised boat structure gives a similar result as previously. The images below show the path the IRC took.

The energy was marginally lower
Activation Energy Calculation & Analysis
The final part of the tutorial is to calculate the activation energy of the reaction via both TS. This is achieved by optimising both chair and boat structure to a higher level of theory (B3LYP/6-31G*) from the HF/3-21G level, then carrying out a frequency analysis.
Firstly, the chair structure was optimised and the log file can be found here. Then a frequency analysis of this structure was carried out and the log file is located here. One imaginary frequency was found which corresponds to the correct rearrangement.
Secondly the boat structure was optimised and the log file can be found here. Then a frequency analysis of this structure was carried out and the log file is located here. One imaginary frequency was found which corresponds to the correct rearrangement.
Comparing the structures of the TS at differing levels of optimisation, there is very little geometrical difference.
There are differences in their energies however. These energies are tabulated below.
Summary of energies (in hartree)
| HF/3-21G | B3LYP/6-31G(d) | |||||
|---|---|---|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | |||
| Chair TS | -231.619322 | -231.466700 | -231.461341 | -234.556983 | -234.414929 | -234.409009 |
| Boat TS | -231.602802 | -231.450932 | -231.445305 | -234.543093 | -234.402337 | -234.396003 |
| Reactant (anti 2) | -231.692535 | -231.539540 | -231.532566 | -234.611703 | -234.469212 | -231.532566 |
*1 hartree = 627.509 kcal/mol
Summary of activation energies (in kcal/mol)
| HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | Expt. | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | at 0 K | |
| ΔE (Chair) | 45.70 | 44.69 | 34.06 | 33.16 | 33.5 ± 0.5 |
| ΔE (Boat) | 55.60 | 54.76 | 41.96 | 41.32 | 44.7 ± 2.0 |
(The template of the tables were taken from the script.)
As can seen from the tables above, the data collected almost exactly matches that found in the script.
At 0K, both the activation energies for the chair and boat are overestimated, when compared to the experimental value. The values modelled at room temperature are closer to the experimental value (at 0K) with each structure. The chair has a lower activation energy in any case and so it would be expected that this form would dominate the TS.
The Diels-Alder Cycloaddition
The next system that was studied was a Diels-Alder system. This consisted of the addition of ethene to 1,3-butadiene to produce cyclohexene, as described by the reaction mechanism below.

Optimisations
The first step was to optimise the reactants individually.
A molecule of 1-3,cisbutadiene was created and optimised to the Semi-empirical/am1 level. The log file can be found here. The molecule was then reoptimised to a higher BLY3P/6-31G(d) level for greater accuracy. The log file can be found here and a Jmol of the optimised molecule is given below.
test molecule |
As can be seen from the jmol, the molecule is not planar and has a dihedral angle of around 30°. This is consist with the literature,which says that the most energetically stable molecule is between the gauche and the planar form, due to steric hindrance between the protruding hydrogens[2]. It is assumed that the best conformation for optimum orbital overlap is the s-cis conformer. As this excercise relies heavily on the overlap of the different MO's, the molecule will be reoptimised with a fixed dihedral angle of 0°, in order to get best overlap with the dienephile.
Fixing the angle and reoptimising gives a s-cis conformer. The log file can be found here.
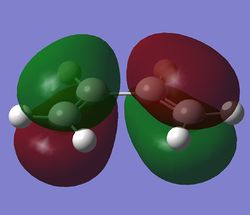
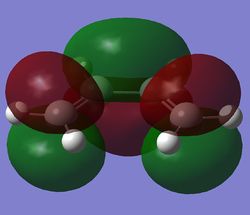
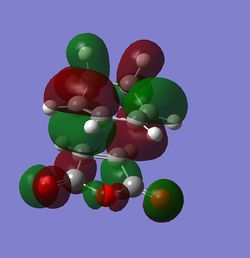
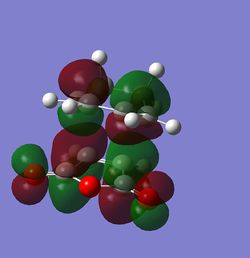
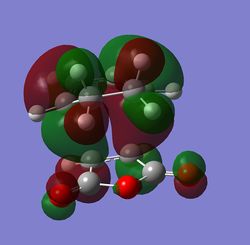
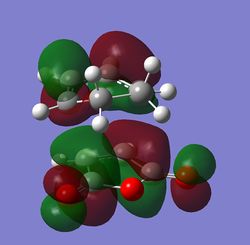
The MOs were then computed and images of the HOMO and the LUMO can be found below. It can be seen that the HOMO is anti-symmetric with respect to eh plane, whereas the LUMO is symmetric.
Transition state geometry
The previously optimised ethene and 1,3-butadiene molecules were placed in the same molecule group and optimised to a minimum whilst fixing the ends of the molecules to be 2.2Å apart. The log file can be found here. Then Gaussain was allowed to derive the previously fixed distances and the molecules were optimised to a (Berny) TS and a frequency calculation was also simultaneously carried out. The log file can be found here. Both calculations used the keyword: OPT=NOEIGEN, in order to avoid imaginary frequencies.
When analysing the vibrations, the lowest energy vibration corresponds to the Diels-Alder Cycloaddition, confirming that this is indeed a TS. The movement of the atoms is synchronous which is expected of a syn cycloaddition. The lowest positive frequency is asynchronous by comparison, looking similar to a 'wagging' of the molecules.
The HOMO and LUMO were then visualised and those images can be found below. It can be seen that the TS HOMO is anti-symmetric with respect to the plane, whereas the LUMO is symmetric.
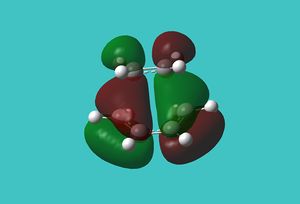

Looking at the HOMO, it is clear that the orbitals that have mixed to produce this orbital are the HOMO of the 1,3-butadiene and the LUMO of the ethene. This is allowed because only orbitals of the same symmetry may mix, and both of these orbitals are anti-symmetric.
Typical sp3 C-C bond lengths are around 1.53Å, whilst sp2 C-C bond lengths are around 1.33Å[3]. The van der Waals radius of C is around 1.7Å[4]. The partyl formed bond in the TS measured 2.12Å. This distance places them between two C atoms which are just touching and have a 'bond' length of 3.4Å (2 x 1.7Å) and 2 C atoms in a single C-C, 3 bond. This suggests some attractive interaction, but it is not quite close enough for Gaussian to recognise a sp3 C-C bond.
Diels-Alder Regioselectivity
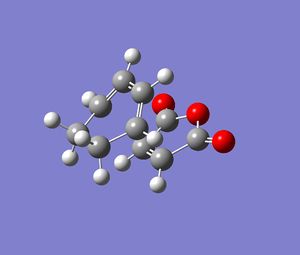
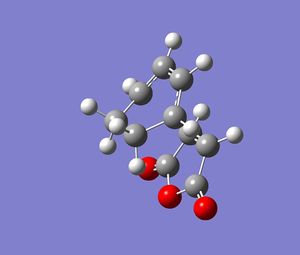
The next step was to investigate the regioselectivity of the Diels-Alder reaction. The reaction studied was that of the addition of cyclohexa-1,3-diene to maleic anhydride. The first step was to individually optimise the molecules at the HF/3-21G level. The log file for the cyclohexa-1,3-diene and maleic anhydride optimisations can be found here and here respectively.
Once optimised, the molecules were treated in the same way as the 'frozen 'coordinate' method as before, in order to find the TS.
The optimised molecules were arranged into a molgroup then the bond distance where the new bonds would form was fixed at 2.2Å, then the rest of the molecules were optimised at the HF/3-21G level. The log file for the endo and exo forms for this optimisation can be found here and here respectively.
Once optimised to a minimum, the previously frozen atoms were then allowed to be derived. The next calculation was an optimisation to the TS and a frequency analysis. The log file for the endo and exo forms for this calculation can be found here and here respectively. Images of the final TS calculated are given below.
Once the vibrations were visualised, it was clear that the lowest vibration was representative of a concerted, syn addition, meaning the two new bonds formed at the same time.
The final energies of the two transition states are tabulated below.
| TS Type | Energy (au) | Energy (kJ/mol) |
|---|---|---|
| Endo | -605.61036812 | 1590030 |
| Exo | -605.60535476 | 1590016 |
The endo form was found to be more stable by around 14 kJ/mol.
The important C-C bond lengths were measured and tabulated below . They are labelled as per the diagram, also below.
| TS type | Length of bond label equivalent A (C--C) | Length of bond label equivalent B (C-C) | Length of bond label equivalent C (C-C) | Length of bond label equivalent D (C-C) |
|---|---|---|---|---|
| Endo | 2.23 | 1.52 | 1.56 | 1.48 |
| Exo | 2.29 | 1.52 | 1.56 | 1.48 |
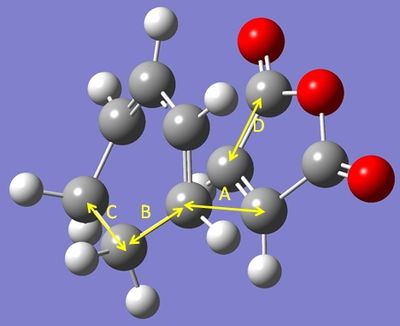
There is little perceptible difference between the C-C bonds of the two forms. the lengths of these bonds are comparable to typical sp3 C-C bonds as described earlier. The new, partially formed bond is less than 2 Van der Waals radii in distance (as described earlier) and so shows an attractive interaction that will go on to form a bond.
The through-space distances between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the opposite fragment (-CH=CH- for the endo and the -CH2-CH2- for the exo) were measured and found to be 2.84Å and 3.03Å respectively. This distance is a compromise between the steric repulsions, and the attractive orbital overlap interactions. The fact that the endo distance is shorted suggests that the attractive orbital overlap effect between the π* C=O bond orbital and the π C=C bond orbital is greater than the steric repulsion. It can be seen that a secondary orbital overlap effect
The HOMOs and the LUMOs of the two product were visulaised and tabulated below.
Examining the HOMOs, it can be seen that there is a nodal plane between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the opposing fragment.
The exo form may be more strained, because it is closer to the more bulky -CH2-CH2- group than the endo form, which is closer to the less bulky -CH=CH- group.
References
- ↑ Benjamin W. Gung, Zhaohai Zhu, and Rebecca A. Fouch Journal of the American Chemical Society 1995 117 (6), 1783-1788
- ↑ J. Rice, B. Liu, T. Lee, and C. M. Rohlfing, Chemical physics letters, 1989, 16
- ↑ F. H. Allen, O. Kennard, D. G. Watson, L. Brammer, and A. G. Orpen, J. Chem. Soc, 1987, 1–19.
- ↑ A. Bondi, J. Phys. Chem., 1964, 68, 441–451.