Rep:Mod:KRM

Compulsory Section

Molecular Optimisations

BH₃

A molecule of BH₃ was created then optimised in Gaussian using the B3LUYP method and a 3-21G basis set. This basis set is of low accuracy, but makes for a quick calculation. The log file can be found here.

BH₃ Optimisation
Parameter	Value
File Type	.log
Calculation Type	FOPT
Basis Set	3-21G
Final Energy	-26.46 au
Gradient	0.00020672 au
Dipole Moment	0.00 Debye
Point Group	D3H
Time to calculate	21 seconds

As can be seen from the data below, it converged successfully.

Item               Value     Threshold  Converged?
 Maximum Force            0.000413     0.000450     YES
 RMS     Force            0.000271     0.000300     YES
 Maximum Displacement     0.001610     0.001800     YES
 RMS     Displacement     0.001054     0.001200     YES
 Predicted change in Energy=-1.071764D-06
 Optimization completed.
    -- Stationary point found.

2nd BH₃ Optimisation

The BH₃ molecule was then reoptimised using a higher basis set (6-31G(d,p)). This basis set can provide a more accurate result. The log file can be found here.
The key word int-ultrafine was also used, as this gives a higher degree of accuracy. Int-ultrafine uses the maximum number of points on the grid used for integrations. From now on, all optimisations will use this keyword for greater accuracy.

2nd BH₃ Optimisation
Parameter	Value
File Type	.log
Calculation Type	FOPT
Basis Set	6-31G(d,p)
Final Energy	-26.62 au
Gradient	0.00014139 au
Dipole Moment	0.00 Debye
Point Group	D3H
Time to calculate	10 seconds

Item               Value     Threshold  Converged?
 Maximum Force            0.000283     0.000450     YES
 RMS     Force            0.000185     0.000300     YES
 Maximum Displacement     0.001125     0.001800     YES
 RMS     Displacement     0.000736     0.001200     YES
 Predicted change in Energy=-4.770182D-07
 Optimization completed.
    -- Stationary point found.

test molecule

The optimised B-H bond distance was found to be 1.19 Å. The optimal H-B-H bond angle was 120.0°

Energies Summary
Basis set of optimisation	Value
3-21G	-26.46 au
6-31+G(d,p)	-26.62 au
Difference	0.15 au

The difference between the two optimisations was found to equal about 0.15 au.

GaBr₃

A molecule of GaBr₃ was created then optimised in Gaussian using the B3LUYP method and a LANL2DZ basis set. The log file can be found here.

Digital repository can be found here: http://hdl.handle.net/10042/25183

GaBr₃ Optimisation
Parameter	Value
File Type	.log
Calculation Type	FOPT
Basis Set	LANL2DZ
Final Energy	-41.70 au
Gradient	0.00402846 au
Dipole Moment	0.0000 Debye
Point Group	D3H
Time to calculate	13.8 seconds

As can be seen from the data below, it converged successfully.

Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000003     0.001800     YES
 RMS     Displacement     0.000002     0.001200     YES
 Predicted change in Energy=-1.282690D-12
 Optimization completed.
    -- Stationary point found.

test molecule

The optimised Br-Ga bond distance was found to be 2.39 Å. This is close to the literature bond length of 2.239Å.^[1]The difference between the two values may be because the basis set used was nto accurate enough. The optimal Br-Ga-Br bond angle was 120.0°. This is as expected as per a symmetrical, trigonal planar molecule.

BBr₃

A molecule of BBr₃ was created then optimised in Gaussian using the B3LUYP method and a GEN basis set. The log file can be found here

Digital repository can be found here: http://hdl.handle.net/10042/25209

BH3 Optimisation
Parameter	Value
File Type	.log
Calculation Type	FOPT
Basis Set	Gen
Final Energy	-64.44 au
Gradient	0.00000382 au
Dipole Moment	0.00 Debye
Point Group	D3H
Time to calculate	18.6 seconds

As can be seen from the data below, it converged successfully.

Item               Value     Threshold  Converged?
 Maximum Force            0.000008     0.000450     YES
 RMS     Force            0.000005     0.000300     YES
 Maximum Displacement     0.000036     0.001800     YES
 RMS     Displacement     0.000023     0.001200     YES
 Predicted change in Energy=-4.027557D-10
 Optimization completed.
    -- Stationary point found.

test molecule

The optimised Br-B bond distance was found to be 1.93 Å. The optimal Br-B-Br bond angle was 120.0°.

Summary and Analysis

Comparing bond distances
Molecule	Bond Distance (Å)
BH₃	1.19
BBr₃	1.93
GaBr₃	2.39

As can be seen from the table above, changing the ligand changes the optimal, average bond length, in this case using Br instead instead of H increases the bond length. H and Br both usually form one bond each, as H is in group 1 and Br in group 7, however the atomic mass of the two elements is very different. Br is around 80 times the mass of H. Br is also more electronegative than H. Br is also larger, having a Van der Waal's (VdW) radius of around 1.9Å^[2], compared to 1.2Å for H^[3]. This would mean that bonds made with these elements would differ in length also, as the VdW radii differ.
As the atoms get larger, orbital overlap becomes weaker, and so the bond is weakened. GaBr₃ has the biggest, most diffuse orbitals and so the weakest bonds.
In all cases, the ligand is more electronegative than the central atom and so electron density is drawn away from the centre to the ligands. This is most pronounced for GaBr₃, where the electronegativity difference is greatest.^[4]

A bond is simply an area of increased electron density between atoms. Gaussview doesn't automatically draw in the expected bonds, perhaps because the distance between them is greater than the traditional bond length that using the VdW radii would predict for a bond. Gaussview may draw bonds by predicting electron density, so when the atoms are far apart, the electron density might be too small to be classed as a bond. When the distance shrinks upon optimisation, a bond is drawn.

Frequency Analysis

BH₃

A frequency analysis of the more higherly optimised BH₃ molecule was then carried out, using the 6-31G(D,P) basis set. The log file can be found here

BH₃ Frequency
Parameter	Value
File Type	.log
Calculation Type	FREQ
Basis Set	6-31G(D,P)
Final Energy	-26.62 au
Gradient	0.00000242 au
Dipole Moment	0.00 Debye
Point Group	D3H
Time to calculate	21.0 seconds

the data below shows that this successfully converges.

Item               Value     Threshold  Converged?
 Maximum Force            0.000005     0.000450     YES
 RMS     Force            0.000002     0.000300     YES
 Maximum Displacement     0.000019     0.001800     YES
 RMS     Displacement     0.000010     0.001200     YES
 Predicted change in Energy=-1.378611D-10
 Optimization completed.
    -- Stationary point found.

The low frequencies are within the ±15 cm^-1 stated requirement, so this can be thought of as the minimum energy point.

Low frequencies ---  -11.9877  -11.9804   -7.0672   -0.0004    0.0260    0.4183
 Low frequencies --- 1162.9723 1213.1375 1213.1377

The table below outlines the different 'real' vibrational modes of BH₃.

BH₃ Vibrational modes
Mode number	Description	Frequency	Point Group Symmetry
1	3 H's bending perpendicular to the plane. B moves in the opposite direction	1162.97	A₂"
2	3 H's rock in-plane with 1 H going in the opposite direction and B staying stationary.	1213.14	E'
3	B and 1H stationary, other H's rock in plane symmetrically	1213.14	E'
4	3 H's stretch symmetrically, in-plane	2582.59	A₁'
5	2 H's stretch in-plane but asymmetrically. B slightly rocks	2715.73	E'
6	3 H's stretch in-plane. " stretch symmetrically, the other stretches asymmetrically	2715.73	E'

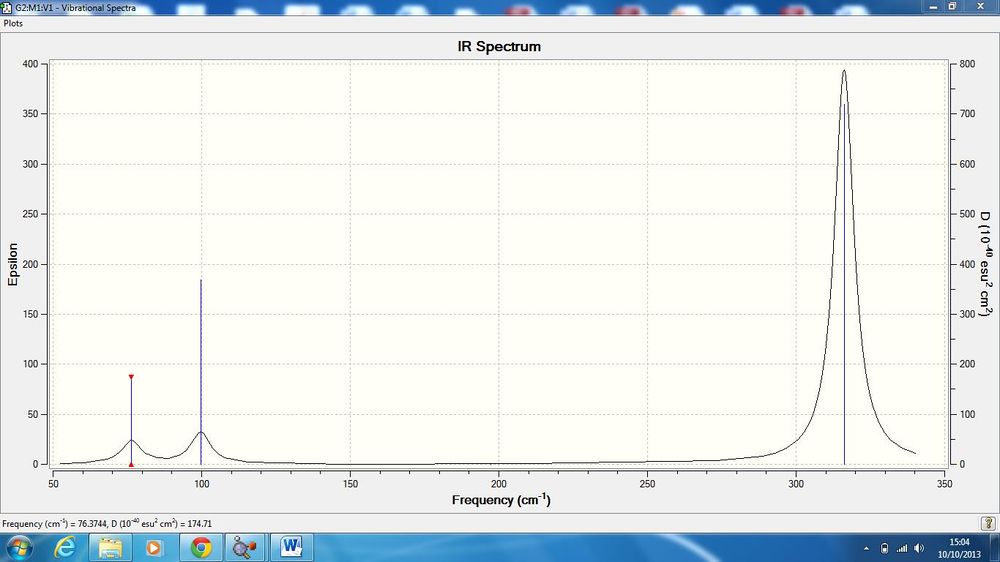
IR Spectrum

The predicted IR spectrum is shown below.

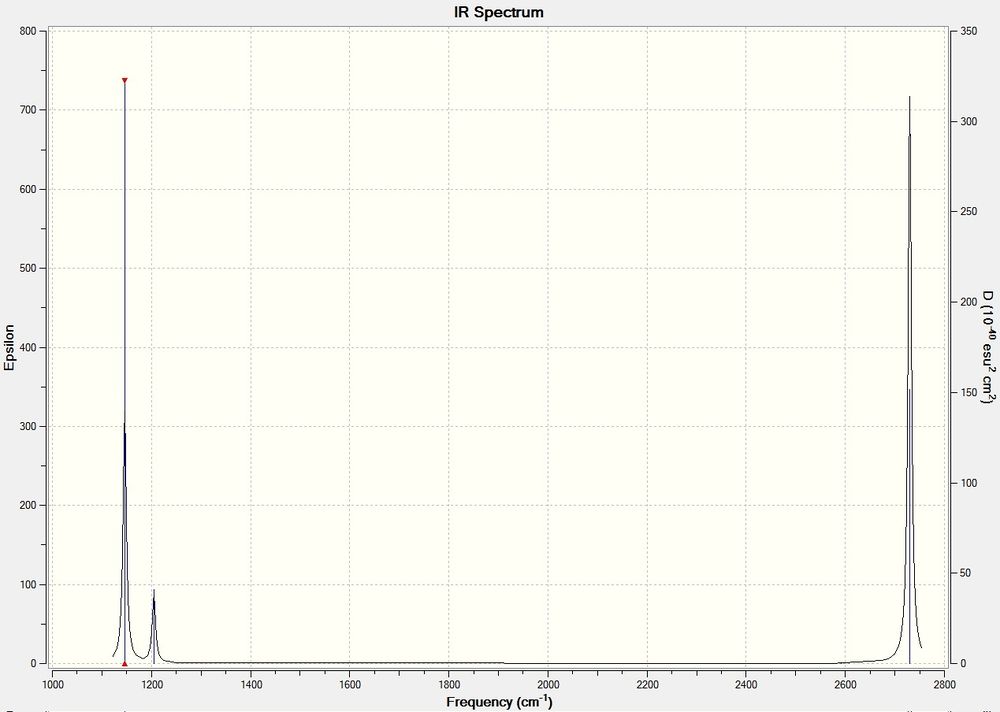
Whilst there are 6 vibrations, there are only 3 peaks visible in the IR spectrum. Mode 4 is totally symmetric, and so does not register with IR, as it requires an asymmetric stretch to create a momentary dipole. Modes 2&3 and 5&6 are degenerate and so have the same energy and so show in the same peak on the spectrum. Only 1 mode (1) is both asymmetric and not degenerate.

GaBr₃

The previously optimised molecule of GaBr₃ was then submitted for frequency analysis using the LANL2DZ basis set.

Digital repository can be found here:http://hdl.handle.net/10042/25325

GaBr₃ Frequency
Parameter	Value
File Type	.log
Calculation Type	FREQ
Basis Set	LANL2DZ
Final Energy	-41.70 au
Gradient	0.00000011 au
Dipole Moment	0.00 Debye
Point Group	D3H
Time to calculate	9.0 seconds

The data shows that it converged successfully.

Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000002     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES
 Predicted change in Energy=-6.142862D-13
 Optimization completed.
    -- Stationary point found.

Low frequencies ---   -0.5252   -0.5247   -0.0024   -0.0010    0.0235    1.2010
 Low frequencies ---   76.3744   76.3753   99.6982

The lowest frequency 'real' modes and 1&2. They are degenerate and at around 76.4 cm^-1. The low frequencies suggest that this is an energetic minimum.

IR Spectrum

Summary and Analysis

Comparing bond distances
Mode	BH₃ frequency (cm^-1)	GaBr₃ frequency (cm^-1)
1	1163	76
2	1213	76
3	1213	100
4	2583	197
5	2716	316
6	2716	316

As can be seen from the table above, there is a large disparity between the two sets of data.
The fundamental vibrational frequency (v) of a bond between two atoms (A&B) can be given by the following equation:

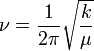
Where 'k' is the spring constant of the bond and μ is the reduced mass of the system, given by:

Where m_A is the mass of atom A, and m_B the mass of atom B.

These equations go some way to explain the disparity between the data set. The mass of both atoms in GaBr₃ are far heavier than those in BH₃. This means the the reduced mass will be much higher, and therefore the vibrational frequency lower, as vibrational frequency is inversely proportional to reduced mass. The spring constant will also vary depending on the atoms used.
The modes are the same, but they have been reordered. Modes 2&3 for BH₃ and 1&2 for GaBr₃ have swapped order.
The spectra are similar in the way that there are three modes grouped at a lower frequency and two grouped at a much higher frequency. The spectrum for BH₃ shows much more intense peaks for the lowest and highest energy modes. GaBr₃ has one very intense peak only, at 316.19 cm_-1. Four modes are grouped together in pairs because these motions correspond to either a stretching (which is of higher energy) or a bending which requires less energy.

The same method basis sets must be used for both the optimisation and the frequency calculation because if different methods are used, the analyses will be using different molecules, then they will be incomparable. Different levels of basis set and method also give differing levels of accuracy and precision.
A frequency analysis tells us whether the position along the potential energy surface that the molecule is at is a maximum or minimum. An optimisation only finds a point of 0 gradient. There are two points of 0 gradient in this example, a minimum energy and a transition state. Optimisation alone does not differentiate between them.

The 6 low frequencies represent the motions of the centre of mass of the molecule. These are significantly smaller than the other frequencies.

BH₃ MO Diagram

The MO's of the previously optimised BH₃ molecule were calculated using the setup below. The log file can be found here

BH₃ MO calculation
Parameter	Value
File Type	.log
Calculation Type	FSP
Basis Set	6-31G9(d,p)
Final Energy	-26.62 au
Gradient	0.00020672 au
Dipole Moment	0.00 Debye
Point Group	D3H
Time to calculate	19 seconds

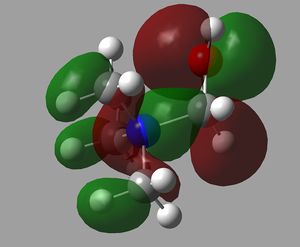
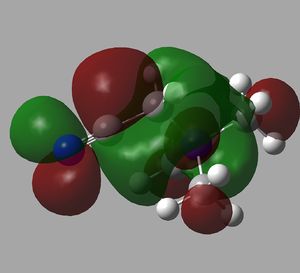
Once the MO's were calculated they were visualised in GaussView. These were then added to an MO diagram drawn on ChemDraw. This is shown below.

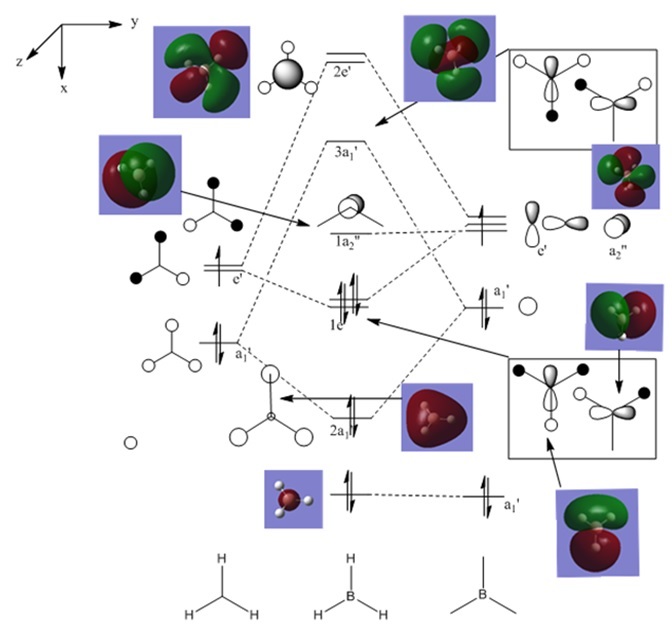
As can be seen, the real and LCAO MO's are very similar. They are almost exactly the same up until the non-bonding orbitals. After that, they start to deviate slightly. This still however shows that qualitative MO theroy is very useful, as all of the occupied orbitals have been estimated with great accuracy.

NH₃ NBO

An NH₃ molecule was created and optimised with the 6-31G(d,p) basis set and the results are shown below. The optimisation log file can be found here

NH₃ Optimisation
Parameter	Value
File Type	.log
Calculation Type	FOPT
Basis Set	6-31G(d,p)
Final Energy	-56.56 au
Gradient	0.00000137 au
Dipole Moment	1.85 Debye
Point Group	C1
Time to calculate	21 seconds

The data below shows the successful convergence of the optimisation.

Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000015     YES
 RMS     Force            0.000001     0.000010     YES
 Maximum Displacement     0.000008     0.000060     YES
 RMS     Displacement     0.000004     0.000040     YES
 Predicted change in Energy=-1.779768D-11
 Optimization completed.
    -- Stationary point found.

A frequency analysis was then carried out to determine if the molecule was correctly optimised. The log file can be found here and is detailed below.

NH₃ Frequency Analysis
Parameter	Value
File Type	.log
Calculation Type	FREQ
Basis Set	6-31G(d,p)
Final Energy	-56.56 au
Gradient	0.00000152 au
Dipole Moment	1.85 Debye
Point Group	C1
Time to calculate	25 seconds

The data below shows a successful convergence.

Item               Value     Threshold  Converged?
 Maximum Force            0.000003     0.000450     YES
 RMS     Force            0.000002     0.000300     YES
 Maximum Displacement     0.000008     0.001800     YES
 RMS     Displacement     0.000003     0.001200     YES
 Predicted change in Energy=-2.187882D-11
 Optimization completed.
    -- Stationary point found.

Low frequencies ---   -9.3678   -8.1299   -5.9522    0.0005    0.0010    0.0012
 Low frequencies --- 1089.3374 1693.9210 1693.9251

Finally a population analysis was carried out on the optimised NH₃. This is detailed below. The log file can be found here.

NH₃ Population analysis
Parameter	Value
File Type	.log
Calculation Type	SP
Basis Set	6-31G(d,p)
Final Energy	-56.56 au
Gradient
Dipole Moment	1.85 Debye
Point Group	C1
Time to calculate	17 seconds

A Natural Bond Orbital Analysis of the NH₃ molecule was then carried out.

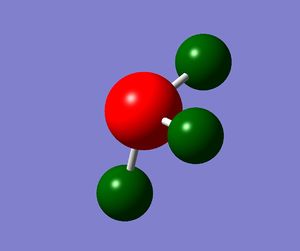
The charge range used was -1.125 to +1.125

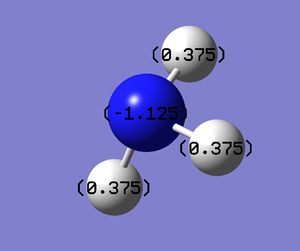
Association energy of NH3 and BH3

NH₃BH₃ Optimisation & Frequency analysis

A molecule of NH₃BH₃ was created then optimised using the same method and basis set as the NH₃ molecule and the BH₃. The log file can be found here

NH₃BH₃ Optimisation
Parameter	Value
File Type	.log
Calculation Type	FOPT
Basis Set	6-31G9d,p)
Final Energy	-83.22 au
Gradient	0.00005975 au
Dipole Moment	5.57 Debye
Point Group	C1
Time to calculate	1 minute 52 seconds

The data below shows a successful convergence.

Item               Value     Threshold  Converged?
 Maximum Force            0.000122     0.000450     YES
 RMS     Force            0.000058     0.000300     YES
 Maximum Displacement     0.000513     0.001800     YES
 RMS     Displacement     0.000296     0.001200     YES
 Predicted change in Energy=-1.631181D-07
 Optimization completed.
    -- Stationary point found.

A frequency analysis of the molecule was then carried out. The log file can be found here

NH₃BH₃ Frequency
Parameter	Value
File Type	.log
Calculation Type	FREQ
Basis Set	6-31G9d,p)
Final Energy	-83.22 au
Gradient	0.00005968 au
Dipole Moment	5.57 Debye
Point Group	C1
Time to calculate	1 minute 2 seconds

The data below shows a successful convergence.

Item               Value     Threshold  Converged?
 Maximum Force            0.000114     0.000450     YES
 RMS     Force            0.000060     0.000300     YES
 Maximum Displacement     0.000579     0.001800     YES
 RMS     Displacement     0.000346     0.001200     YES
 Predicted change in Energy=-1.730768D-07
 Optimization completed.
    -- Stationary point found.

Low frequencies ---    0.0006    0.0011    0.0015   16.8372   17.4093   37.2732
 Low frequencies ---  265.8194  632.2112  639.3256

The lowest mode occurs at 266 cm^-1

Summary and Analysis

All of the data regarding the energies of NH₃, BH₃ and NH₃BH₃ were then correlated in the table below

Molecular energies
Molecule	Energy (au)
BH₃	-26.62
NH₃	-56.56
NH₃BH₃	-83.22

The energy difference can be given by the following formula: ΔE=E(NH3BH3)-[E(NH3)+E(BH3). According to this formula and the data, the energy difference is -0.05159668 au. This is equivalent to around -135.47 kJ/mol. The dissociation energy is therefore +135.47 kJ/mol.

Ionic Liquids: Desginer Solvents Mini Project

Molecules of [N(CH₃)₄]⁺, [P(CH₃)₄]⁺ and [S(CH₃)₃]⁺ were created and optimised. The details are shown below.

Optimisations and Analyses

[N(CH₃)₄]⁺

The digital repository can be found here:http://hdl.handle.net/10042/25478. The log file can be found here

[N(CH₃)₄]⁺ Optimisation
Parameter	Value
File Type	.log
Calculation Type	FOPT
Basis Set	6-31G(d,p)
Final Energy	-214.18 au
Gradient	0.00004413 au
Dipole Moment	22.56 Debye
Point Group	C1
Time to calculate	2 minutes 57 seconds

As can be seen from the data below, it converged successfully.

Item               Value     Threshold  Converged?
 Maximum Force            0.000068     0.000450     YES
 RMS     Force            0.000027     0.000300     YES
 Maximum Displacement     0.000453     0.001800     YES
 RMS     Displacement     0.000124     0.001200     YES
 Predicted change in Energy=-8.897040D-08
 Optimization completed.
    -- Stationary point found.

The optimised molecule was then subjected to a frequency analysis to check the validity of the optimisation. The log file can be found here. The digital repository can be found here: http://hdl.handle.net/10042/25719

[N(CH₃)₄]⁺ Frequency Analysis
Parameter	Value
File Type	.log
Calculation Type	FREQ
Basis Set	6-31G(d,p)
Final Energy	-214.18 au
Gradient	0.00004409 au
Dipole Moment	22.56 Debye
Point Group	C1
Time to calculate	6 minutes 42 seconds

As can be seen from the data below, it converged successfully.

Item               Value     Threshold  Converged?
 Maximum Force            0.000110     0.000450     YES
 RMS     Force            0.000044     0.000300     YES
 Maximum Displacement     0.001077     0.001800     YES
 RMS     Displacement     0.000376     0.001200     YES
 Predicted change in Energy=-9.424128D-08
 Optimization completed.
    -- Stationary point found.

Low frequencies ---  -13.0055   -0.0009   -0.0008   -0.0007    6.2187   12.1424
 Low frequencies ---  181.5408  279.9741  286.8026

[P(CH₃)₄]⁺

The log file can be found here, The digital depository can be found here: http://hdl.handle.net/10042/25479.

[P(CH₃)₄]⁺ Optimisation
Parameter	Value
File Type	.log
Calculation Type	FOPT
Basis Set	6-31G(d,p)
Final Energy	-500.83 au
Gradient	-500.83 au
Dipole Moment	22.56 Debye
Point Group	C1
Time to calculate	5 minutes 48 seconds

As can be seen from the data below, it converged successfully.

Item               Value     Threshold  Converged?
 Maximum Force            0.000190     0.000450     YES
 RMS     Force            0.000037     0.000300     YES
 Maximum Displacement     0.001167     0.001800     YES
 RMS     Displacement     0.000376     0.001200     YES
 Predicted change in Energy=-2.475395D-07
 Optimization completed.
    -- Stationary point found.

The optimised molecule was then subjected to a frequency analysis to check the validity of the optimisation. The log file can be found here. The digital depository can be found here:http://hdl.handle.net/10042/25720

[P(CH₃)₄]⁺ Frequency Analysis
Parameter	Value
File Type	.log
Calculation Type	FREQ
Basis Set	6-31G(d,p)
Final Energy	-500.83 au
Gradient	0.00003221 au
Dipole Moment	22.56 Debye
Point Group	C1
Time to calculate	7 minutes 29 seconds

Item               Value     Threshold  Converged?
 Maximum Force            0.000119     0.000450     YES
 RMS     Force            0.000032     0.000300     YES
 Maximum Displacement     0.000699     0.001800     YES 
 RMS     Displacement     0.000214     0.001200     YES 
 Predicted change in Energy=-3.966969D-07

[S(CH₃)₃]⁺

The log file can be found here. The digital depository can be found here: http://hdl.handle.net/10042/25480.

[S(CH₃)₃]⁺ Optimisation
Parameter	Value
File Type	.log
Calculation Type	FOPT
Basis Set	6-31G(d,p)
Final Energy	-517.68 au
Gradient	0.00000343 au
Dipole Moment	22.12 Debye
Point Group	C1
Time to calculate	10 minutes 57 seconds

As can be seen from the data below, it converged successfully.

Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000015     YES
 RMS     Force            0.000000     0.000010     YES
 Maximum Displacement     0.000036     0.000060     YES
 RMS     Displacement     0.000012     0.000040     YES
 Predicted change in Energy=-1.298246D-11
 Optimization completed.
    -- Stationary point found.

The optimised molecule was then subjected to a frequency analysis to check the validity of the optimisation. The log file can be found here. The digital depository can be found here: http://hdl.handle.net/10042/25724.

[S(CH₃)₃]⁺ Frequency Analysis
Parameter	Value
File Type	.log
Calculation Type	FREQ
Basis Set	6-31G(d,p)
Final Energy	-517.68 au
Gradient	0.00000344 au
Dipole Moment	22.12 Debye
Point Group	C1
Time to calculate	3 minutes 58 seconds

As can be seen from the data below, it converged successfully.

Item               Value     Threshold  Converged?
 Maximum Force            0.000007     0.000450     YES
 RMS     Force            0.000003     0.000300     YES
 Maximum Displacement     0.000445     0.001800     YES
 RMS     Displacement     0.000138     0.001200     YES
 Predicted change in Energy=-3.778948D-10
 Optimization completed.
    -- Stationary point found.

Low frequencies ---  -18.2424  -15.0956   -0.0029   -0.0020    0.0030   23.3416
 Low frequencies ---  163.3267  196.9306  201.5785

Geometry Analysis

A tabulated view of the bond distances is given below. The central heteroatom is represented by 'X'. Å is the unit of distance in all cases.

Tabulated Distances
Molecule	C-X Bond Distance	C-H Bond Distance	C-X-C Bond Angle
N(CH₃)₄]⁺	1.509	1.090	109.5°
P(CH₃)₄]⁺	1.816	1.093	109.4°
S(CH₃)₃]⁺	1.823	1.092	102.7°

The N(CH₃)₄]⁺ and P(CH₃)₄]⁺ molecules adopt the tetrahedral geometry, whilst the S(CH₃)₃]⁺ adopts a trigonal pyramidal geometry. Because the two larger molecule have the same structure, they have very similar bond angles, close to the perfect bond angle of a tetrahedral arrangement (109.5°). The bond angles of S(CH₃)₃]⁺ are lower than that of a tetrahedral, as the lone pair on the sulphur pushes the methyl groups away, contracting the angle to less than 109.5°. In order of size, the heteroatoms are N<S<P. This is roughly in line with C-X bond distances. Bigger atoms tend to make bigger bonds. The C-S bond might be longer than expected. This could be because of lone pair repulsion lengthening the bond. The C-H distance stays very similar throughout which suggests that the central atom is too far away to directly influence this bond.

MO and NBO Analysis

[N(CH₃)₄]⁺

A population analysis was carried out on the optimised [N(CH₃)₄]⁺. This is detailed below. The log file can be found here and the digital depository here: http://hdl.handle.net/10042/25725

[N(CH₃)₄]⁺ Population analysis
Parameter	Value
File Type	.log
Calculation Type	SP
Basis Set	6-31G(d,p)
Final Energy	-214.18 au
Gradient
Dipole Moment	22.56 Debye
Point Group	C1
Time to calculate	52 seconds

[P(CH₃)₄]⁺

A population analysis was carried out on the optimised [P(CH₃)₄]⁺. This is detailed below. The log file can be found here and the digital repository here: http://hdl.handle.net/10042/25726.

[P(CH₃)₄]⁺ Population analysis
Parameter	Value
File Type	.log
Calculation Type	SP
Basis Set	6-31G(d,p)
Final Energy	-500.83 au
Gradient
Dipole Moment	22.56 Debye
Point Group	C1
Time to calculate	46 seconds

[S(CH₃)₃]⁺

A population analysis was carried out on the optimised [S(CH₃)₃]⁺. This is detailed below. The log file can be found here and the digital repository here: http://hdl.handle.net/10042/25727.

[S(CH₃)₃]⁺ Population analysis
Parameter	Value
File Type	.log
Calculation Type	SP
Basis Set	6-31G(d,p)
Final Energy	-517.68 au
Gradient
Dipole Moment	22.12 Debye
Point Group	C1
Time to calculate	33 seconds

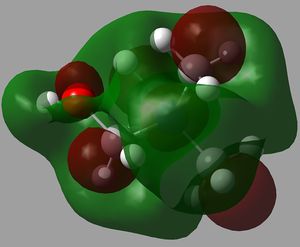
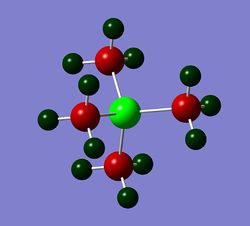
Charge Distribution Images

The images of the charge distribution analysis are tabulated below. All coloured images use a scale which ranges from -1.7 to +1.7.

Charge Distribution Images
Image Type	[N(CH₃)₄]⁺	[P(CH₃)₄]⁺	[S(CH₃)₃]⁺
Colour atom by charge
Atomic charge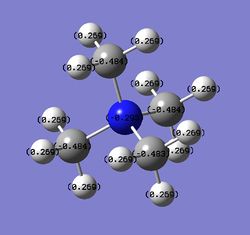

Charge Distribution Analysis

The data from the NBO analysis was collated below.

NBO charge analysis
Ion	Heteroatom charge	C charge	H charge	Heteroatom electronegativity
[N(CH₃)₄]⁺	-0.295	-0.484	+0.269	3.04
[P(CH₃)₄]⁺	+1.668	-1.06	+0.298	2.19
[S(CH₃)₃]⁺	+0.917	-0.846	+0.279	2.58

As can be seen from above, changing the heteroatom wildly changes the charge distribution. H always has a slight positive charge. This doesn't change significantly from complex to complex. Carbon is more electronegative than H (2.55 to 2.1 respectively) and so always has a negative charge. The difference in electronegativity between the heteroatom and the C atom is mirrored by the difference in electronegativity. N is the most electronegative, and so manages to draw electron density to itself preferentially over the C atoms better than the other heteroatoms. Even so, it is still more positively charged than the the C atom. This suggests that the extra positive charge that the ion has is broadly spread over the ion, but slightly concentrated on the N atom.
The other ions spread the positive charge much more poorly and it is localised on the central heteroatom. Even though, for instance, P is more electronegative than H, it carries much more negative charge. P is a lot bigger than C and so would have a poor orbital overlap. This may mean that it is more difficult to delocalise the positive charge across more atoms. S has a better orbital overlap and N the best. When the heteroatom is P or S, the changes are so localised, the bonding is ionic-like.

[N(CH₃)₄]⁺ MO Visualisation

All of the MOs for [N(CH₃)₄]⁺ were generated with Gaussview. The occupied, non-core MOs are tabulated below.

[N(CH₃)₄]⁺
6^th MO	7^th MO	8^th MO	9^th MO

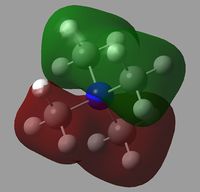
10^th MO	11^th MO	12^th MO	13^th MO

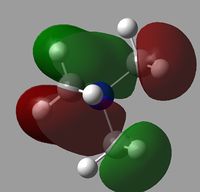14^th MO	15^th MO	16^th MO	17^th MO

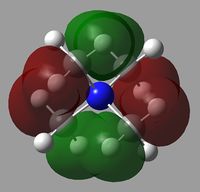18^th MO	19^th MO	20^th MO	21^th MO

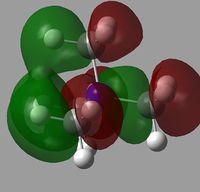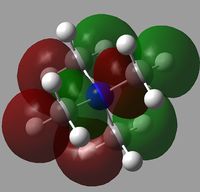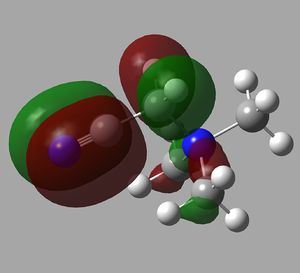
The orbital interactions of 5 of the above MOs were investigated more deeply. The results are displayed below.

[N(CH₃)₄]⁺
6^th MO	8^th MO	10^th MO

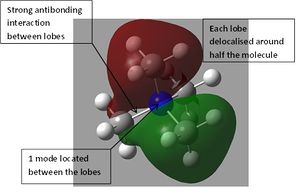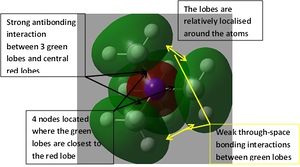
12^th MO	17^th MO

C-X Bond Contribution

The C-X bonds were analysed using the NBO analysis and the data tabulated below.

NBO bond analysis
Ion	C % contribution to bond	X % contribution to bond
[N(CH₃)₄]⁺	37	63
[P(CH₃)₄]⁺	60	40
[S(CH₃)₃]⁺	49	51

The results above follow the trend of relative electronegativities, as before. The more electronegative the X compared to C, the less it contributes to the C-X bond. This is the same trend as when analysing charge distribution.

[NR₄]⁺

The [NR₄]⁺ system is traditionally described by having the positive charge on the N. The [N(CH₃)₄]⁺ ion analysed previously is a good representative of the [NR₄]⁺ system.
If the positive charge was entirely placed on the central N, it could be assumed that the charge of that nitrogen would be close to +1. Actually, it was estimated the charge would be -0.3. This large discrepancy suggests that the positive charge is in fact not localised entirely on the N but spread across the molecule. This is further suggested by the fact that for this system, the range of charges is small; far smaller than for the other systems with different heteroatoms. A formal charge solely on the N is perhaps not helpful. A better system might be to draw the charge as across the whole molecule and not try to localise it on any one atom.

Influence of Functional Groups

A molecule of [N(CH₃)₃(CH₂OH]⁺ was created then optimised. The log file can be found here

[N(CH₃)₃(CH₂OH]⁺ Optimisation
Parameter	Value
File Type	.log
Calculation Type	FOPT
Basis Set	6-31G(d,p)
Final Energy	-289.39470781 au
Gradient	0.00000081 au
Dipole Moment	22.3599 Debye
Point Group	C1
Time to calculate	55 minutes 48 seconds

As can be seen from the data below, it converged successfully.

Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000015     YES
 RMS     Force            0.000000     0.000010     YES
 Maximum Displacement     0.000032     0.000060     YES
 RMS     Displacement     0.000007     0.000040     YES
 Predicted change in Energy=-3.016813D-11
 Optimization completed.
    -- Stationary point found.

The optimised molecule was then subjected to a frequency analysis to check the validity of the optimisation. The log file can be found here

[N(CH₃)₃(CH₂OH]⁺ Frequency Analysis
Parameter	Value
File Type	.log
Calculation Type	FREQ
Basis Set	6-31G(d,p)
Final Energy	-289.39470611 au
Gradient	0.00002667 au
Dipole Moment	22.3600 Debye
Point Group	C1
Time to calculate	9 minutes 35 seconds

A molecule of [N(CH₃)₃(CH₂CN]⁺ was created then optimised. The log file can be found here

[N(CH₃)₃(CH₂CN]⁺ Optimisation
Parameter	Value
File Type	.log
Calculation Type	FOPT
Basis Set	6-31G(d,p)
Final Energy	-306.39376108 au
Gradient	0.00000041 au
Dipole Moment	21.4650 Debye
Point Group	C1
Time to calculate	13 minutes 32 seconds

As can be seen from the data below, it converged successfully.

Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000015     YES
 RMS     Force            0.000000     0.000010     YES
 Maximum Displacement     0.000011     0.000060     YES
 RMS     Displacement     0.000003     0.000040     YES
 Predicted change in Energy=-4.728936D-12
 Optimization completed.
    -- Stationary point found.

The optimised molecule was then subjected to a frequency analysis to check the validity of the optimisation. The log file can be found here

[N(CH₃)₃(CH₂CN]⁺ Frequency Analysis
Parameter	Value
File Type	.log
Calculation Type	FREQ
Basis Set	6-31G(d,p)
Final Energy	-306.39376656 au
Gradient	0.00002430 au
Dipole Moment	21.4650 Debye
Point Group	C1
Time to calculate	10 minutes 26 seconds

MO and NBO analysis

A population analysis was carried out on the optimised [N(CH₃)₃(CH₂OH]⁺. This is detailed below. The log file can be found here.

[N(CH₃)₃(CH₂OH]⁺ Population analysis
Parameter	Value
File Type	.log
Calculation Type	SP
Basis Set	6-31G(d,p)
Final Energy	-289.39470611 au
Gradient
Dipole Moment	22.3600 Debye
Point Group	C1
Time to calculate	42 seconds

A population analysis was then carried out on the optimised [N(CH₃)₃(CH₂CN]⁺. This is detailed below. The log file can be found here.

[N(CH₃)₃(CH₂OH]⁺ Population analysis
Parameter	Value
File Type	.log
Calculation Type	SP
Basis Set	6-31G(d,p)
Final Energy	-306.39376656 au
Gradient
Dipole Moment	21.4650 Debye
Point Group	C1
Time to calculate	55 seconds

Charge Distribution Images

The images of the charge distribution analysis are tabulated below. All coloured images use a scale which ranges from -0.8 to +0.8, where bright green is most positive and bright red is most negative.

Charge Distribution Images
Image Type	[N(CH₃)₃(CH₂OH]⁺	[N(CH₃)₃(CH₂CN]⁺
Colour atom by charge
Atomic charge

NBO Charge Analysis

The charge distribution data from the NBO analysis was collated below. The OH or CN group was named the 'X' group. The C between the X group and the central N atom was named the bridging C

NBO charge analysis
Ion	Central N charge	C (in CH₃) charge	Bridging C charge
[N(CH₃)₃(CH₂OH]⁺	-0.322	-0.492	+0.088
[N(CH₃)₃(CH₂CN]⁺	-0.289	-0.488	-0.385

As -OH is an electron donating group, it is to be expected that the rest of the molecule would have higher electron density than the corresponding molecule with a -CN group, as -CN is electron withdrawing. It can be seen that changing the X group keeps the central N and attached CH₃ broadly similar in terms of charge distribution. The significant change comes when looking at the bridging C. It would be expected that a group adjacent to an electron donating group would be comparatively negatively charged and vice versa. However, the opposite effect is seen here. O is very electronegative and so pulls electron density from the adjacent C, causing it to be relatively positively charged. The bridging C when the X group is -CN experiences no such effect, as it's neighboring atom is also C.
This suggests that the electron donating/withdrawing nature of an X group in reality means little to the central N and CH₃ groups.

HOMO/LUMO Comparison

The HOMO and LUMO for [N(CH₃)₄]⁺, [N(CH₃)₃(CH₂OH]⁺ and [N(CH₃)₃(CH₂CN]⁺ were visualised and tabulated below.

HOMO/LUMO comparisons
Ion type	HOMO energy (au)	LUMO energy (au)	HOMO/LUMO gap (au)
[N(CH₃)₄]⁺	-0.455	-0.068	0.387
[N(CH₃)₃(CH₂OH]⁺	-0.488	-0.125	0.363
[N(CH₃)₃(CH₂CN]⁺	-0.500	-0.182	0.318

It can be seen that changing the molecules can drastically change the generated MO. In terms of shape and appearance, changing th X group changes the HOMOs to an entirely new form. The LUMO of [N(CH₃)₄]⁺ adopts a 'plum-pudding' appearance, where the general cloud of one lobe is regularly punctuated by opposing lobes. This element of the 'plum-pudding' MO is retained when changing the X group, but now with additional AOs from the X group.
The energy of the MOs (both HOMO and LUMO) decrease when the X group changes; with the biggest decrease coming when the X group is -CN. The HOMO-LUMO gap has also gotten smaller, in the order [N(CH₃)₄]⁺>[N(CH₃)₃(CH₂OH]⁺>[N(CH₃)₃(CH₂CN]⁺.
Generally lower energy orbitals leads to increased stability and unreactivity. It might be expected that [N(CH₃)₃(CH₂CN]⁺would be a more stable cation than [N(CH₃)₄]⁺ and perhaps form more stable ionic structures.
A smaller HOMO-LUMO gap means that it is easier to promote an electron to the LUMO from the HOMO. This also means that emitted light as a consequence this promotion then demotion will be of lower energy and longer wavelength.

Conclusion

A number of complexes were created, optimised, then investigated in a number of ways. I found that computational methods were a good way to predict real-life properties of molecules and my data was close to that of empirical data from the literature.
I was surprised that replacing an electron withdrawing group with an electron donating group (as when the influence of functional groups was investigated) had little effect on the central N. I would have expected a more significant effect.

References

↑ B. Réffy, M. Kolonits, and M. Hargittai, Journal of molecular structure, 1998. DOI:10.1016/S0022-2860(97)00420-1
↑ Handbook of Chemistry and Physics, 65th Ed. (1984), CRC Press and "Chemical Systems"
↑ R. Rowland and R. Taylor, The Journal of Physical Chemistry, 1996, 3654, 7384–7391
↑ Cotton, F. A.; Wilkinson, G. (1988). Advanced Inorganic Chemistry (5th ed.). Wiley. p. 1385. ISBN 978-0-471-84997-1.

[1] B. Réffy, M. Kolonits, and M. Hargittai, Journal of molecular structure, 1998. DOI:10.1016/S0022-2860(97)00420-1

[2] Handbook of Chemistry and Physics, 65th Ed. (1984), CRC Press and "Chemical Systems"

[3] R. Rowland and R. Taylor, The Journal of Physical Chemistry, 1996, 3654, 7384–7391

[4] Cotton, F. A.; Wilkinson, G. (1988). Advanced Inorganic Chemistry (5th ed.). Wiley. p. 1385. ISBN 978-0-471-84997-1.

[1]

[2]

[3]

[4]

Compulsory Section

Molecular Optimisations

BH3

2nd BH3 Optimisation

GaBr3

BBr3

Summary and Analysis

Frequency Analysis

BH3

IR Spectrum

GaBr3

IR Spectrum

Summary and Analysis

BH3 MO Diagram

NH3 NBO

Association energy of NH3 and BH3

NH3BH3 Optimisation & Frequency analysis

Summary and Analysis

Ionic Liquids: Desginer Solvents Mini Project

Optimisations and Analyses

[N(CH3)4]+

[P(CH3)4]+

[S(CH3)3]+

Geometry Analysis

MO and NBO Analysis

[N(CH3)4]+

[P(CH3)4]+

[S(CH3)3]+

Charge Distribution Images

Charge Distribution Analysis

[N(CH3)4]+ MO Visualisation

C-X Bond Contribution

[NR4]+

Influence of Functional Groups

MO and NBO analysis

Charge Distribution Images

NBO Charge Analysis

HOMO/LUMO Comparison

Conclusion

References

BH₃

2nd BH₃ Optimisation

GaBr₃

BBr₃

BH₃

GaBr₃

BH₃ MO Diagram

NH₃ NBO

NH₃BH₃ Optimisation & Frequency analysis

[N(CH₃)₄]⁺

[P(CH₃)₄]⁺

[S(CH₃)₃]⁺

[N(CH₃)₄]⁺

[P(CH₃)₄]⁺

[S(CH₃)₃]⁺

[N(CH₃)₄]⁺ MO Visualisation

[NR₄]⁺