Rep:Mod:KMF14TS
Transition States of Diels Alder Reactions
Introduction
Minima are calculated on gaussian by varying the position of each nucleus to find the lowest energy arangement of the molecule. At the minimum energy the potential energy diagram has a gradient of zero and at either side of the minimum the gradient increases.
Transition states are calculated by finding the maximum energy on the lowest energy pathway between the reactants and the products on a potential energy surface.
Gaussian calculates frequencies using a harmonic oscillator model where the frequency is proportional to the square root of the force constant. The force constant is equal to the second derivative of the energy with respect to the positions of the nuclei.
A frequency calculation at the minimum should provide no imaginary frequencies as the second derivative of the energy is positive. A frequency calculation at the transition state should provide an imaginary frequency as given it must curve downwarrds and therefore have a negative second derivative and the square root of a negative number is imaginary.
Nf710 (talk) 11:54, 7 April 2017 (BST) This description of a TS is somewhat lacking. The TS has positive second derivatives in all dimensions of the PES apart from 1. the reaction coordinate.
Reaction of Butadiene and ethylene


(Fv611 (talk) 15:49, 5 April 2017 (BST) You used the wrong symmetry labels. Additionally, the HOMO is a product of S/S interactions, and the HOMO-1 is a product of the AS/AS interaction, while you have switched them around. Furthermore, your AS TS HOMO is drawn wrong. Also, you seem to have attributed a lower energy to the TS MOs resulting of antibonding interactions, whereas the opposite is true. Finally, you forgot to fill in the electrons of the TS MOs.)
| Butadiene | |
| HOMO | LUMO |
|---|---|
 |
|
| Ethene | |
| HOMO | LUMO |
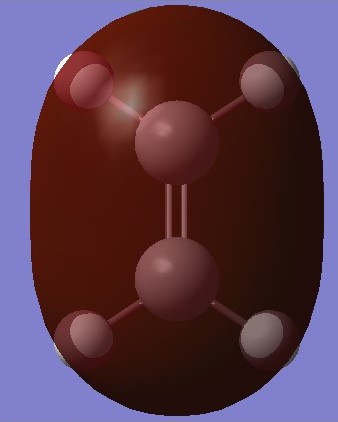 |
|
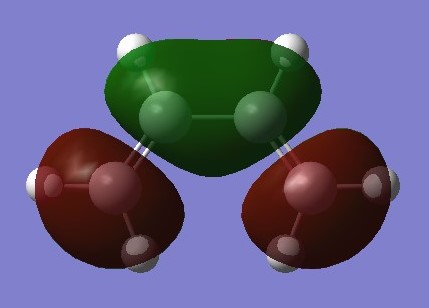
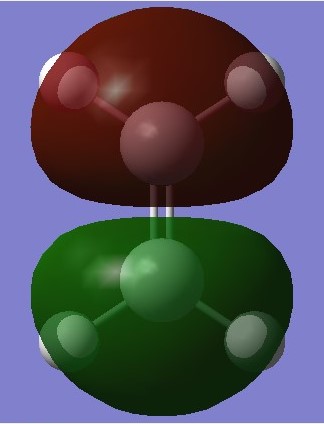
Any MOs of the same symmetry may overlap but orbitals of different symmetries may not. Symmetries are shown by the parity labels g and u where 'g and g' interactions and 'u and u' interactions have a non zero overlap integral but the overlap integral for 'g and u' interactions is 0. This can be shown in the transition state diagrams which show the diene HOMO reacting with the ethene LUMO and vice versa as the orbitals are clearly labelled in the above orbital diagram. This coresponds well with the molecular orbital diagrams as shown below of the transition state which show u-u and g-g overlap but not u-g overlap.
| MO diagrams of butadiene and ethene transition state | |
| 2nd LUMO | LUMO |
|---|---|
 |

|
| HOMO | 2nd HOMO |
 |

|
(Fv611 (talk) 15:49, 5 April 2017 (BST) You didn't label assign any symmetry label to your TS MOs, and you switched HOMO and HOMO-1 (the one you indicate as 2nd HOMO is actually the HOMO).)
| Reactants Bonds | Bond Length | Transition States Bonds | Bond Length | Products Bonds | Bond Length | |
|---|---|---|---|---|---|---|
| ethene | 1.32731 A | ethene | 1.35580 A | ethene | 1.53460 A | |
| diene C=C | 1.33533 A | diene C=C | 1.35663 A | diene C-C | 1.50084 A | |
| diene C-C | 1.46837 A | diene C-C | 1.46837 A | diene C=C | 1.33694 A | |
| forming C-C bond | 2.20723 A | New C-C bond | 1.53714 A |
In general the bond lengths increase from reactants to transition states to products. Exceptions being the single bond in the diene (starting material)and the newly formed carbon carbon bonds The van der Waals radius of carbon is 1.7 A and so two carbon atoms purely interacting through van der Waals forces should have a distance of 3.4 A. The partly formed C-C bonds therefore have overlapping van der Waals radii. The average sp3 C-C bond length is 1.54 A and the average sp2 C-C bond length is 1.47 A
 Woodward Hoffman rules show that the formation of the two bonds are synchronous
(Fv611 (talk) 15:49, 5 April 2017 (BST) As you didn't include a log file, or mentioned whether there is a negative frequency, I can't be sure you reached the TS.)
Woodward Hoffman rules show that the formation of the two bonds are synchronous
(Fv611 (talk) 15:49, 5 April 2017 (BST) As you didn't include a log file, or mentioned whether there is a negative frequency, I can't be sure you reached the TS.)
Reaction of Cyclohexadiene and 1,3-Dioxole
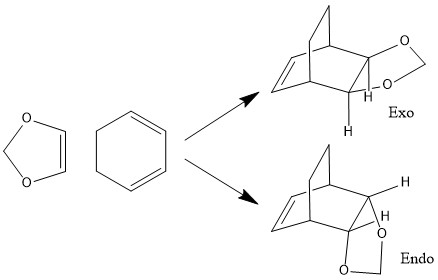
| Endo Transition State | |
| HOMO | LUMO |
|---|---|
 |

|
| Exo Transition State | |
| HOMO | LUMO |
 |

|
(No MO diagram, and these MOs above don't look like their geometries had converged. Perhaps bonds were frozen? This would give you the wrong energies for calculations if you used this geometry Tam10 (talk) 16:47, 3 April 2017 (BST))
A normal diels alder reaction requires an electron rich diene and an electron poor dienophile. The electron rich dienes molecular orbitals are higher in energy to that of the electron poor dienophile. The HOMO of the diene and the LUMO of the dienophile are more similar in energy than the HOMO dienophile and the LUMO of the diene.
The inverse demand diels alder reaction requires an electron-poor diene and an electron rich dienophile. This changes the orbital diagram somewhat so that the LUMO of the diene and HOMO of the diene are most similar in energy.
Given that the HOMO diene and LUMO dienophile gap is smaller than the LUMO diene HOMO dienophile gap, this is a nomal diels alder reaction.
| Reaction type | Reactant Energy kJ mol-1 | TS energy kJ mol-1 | Product Energy kJ mol-1 |
|---|---|---|---|
| Endo | 0 | 157.63 | -67.65 |
| Exo | 0 | 165.98 | -63.24 |
This shows that the endo transition state is kinetically favourable as it is lowest in enegy and the endo product is also more stable making this reaction both thermodynamically and kinetically favouring the endo product.
The HOMO of the endo transition state shows that orbitals on oxygen are also involved in the reaction. It is believed that as a secondary effect the oxygen orbitals may stabilise the transition state with favourable (non bonding)interactions between the two molecules, despite it sterically being less favourable to have the two molecules on top as in an endo transition state.
Nf710 (talk) 12:03, 7 April 2017 (BST) You should have put some diagrams in here to back up your point. Also is in an inverse reaction. And the endo is sterically less hindered. A diagram would have proved this. Your energies are correct however and you have therefore got the correct conclusion.
Diels Alder vs Chelotropic Reactions




| Reaction type | Reactant Energy kJ mol-1 | TS energy kJ mol-1 | Product Energy kJ mol-1 |
|---|---|---|---|
| Endo | 0 | 46.34 | -134.17 |
| Exo | 0 | 50.19 | -130.23 |
| Chelotropic | 0 | 64.39 | -188.02 |
IRC of chelotropic transition state
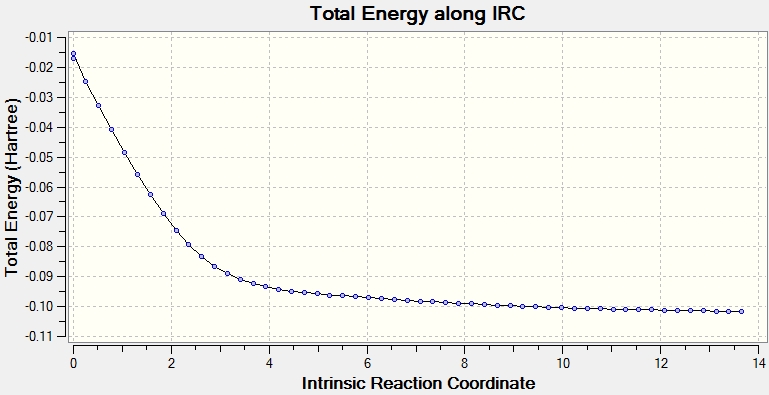
The diagrams should show the IRC of the transition state however they don't. A proper IRC should have a gradient of 0 either side of the peak but I'm am terrible at actually finding the proper transition state so it doesn't (and sort of ran out of time to try)
(You must ask a demo if you have problems finding geometries. There's just one step that you've missed out in the calculations that we could have helped you with. Tam10 (talk) 16:47, 3 April 2017 (BST))
The endo transition state has the lowest energy and therefore is the most kinetically favoured product while the chelotropic product is the most stable thermodynamically as it has the lowest product energy
Xylylenes structure is very close to that of benzene and can easily form an aromatic ring in order to stabilise itself either by reacting with a double bond or in a ring closing metathesis style reaction. During the course of each of the above reactions an aromatic ring is formed stabilising the reaction and making it less likely to be a reversible reaction



