Using Gaussian to optimise molecules

NH3 Molecule

Properties

The NH₃ molecule on the left was optimised using a B3LYP method and a 6-31G(d,p) basis set with the following steps:

Step 1: In the first optimisation step, the N-H bond lengths are 1.3 Angstrom which is too far apart for a covalent bond to form.
Step 2: As the optimisation occurs the hydrogen atoms are pulled closer to the Nitrogen atom in the centre.
Step 3: The hydrogen atoms now experience an attractive force from the Nitrogen atom and are close enough to form covalent bonds.
Step 4: The N-H bonds angle changes from 101.721 to 104.780 to reduce strain in the molecule.
Error creating thumbnail: File with dimensions greater than 12.5 MP

Step 5: The bond angle changes again from 104.780 to 105.749.
Step 6 of the optimisation process.
Step 7: The optimised NH₃ molecule.

Molecule Name	Ammonia (NH₃)
Calculation Method	RB3LYP
Basis set	6-31G(d,p)
E(RB3LYP)	-56.5577687 a.u
Point Group	C3V
Optimised N-H bond length	1.01798Å
Optimised N-H bond angle	105.741°

Link to the optimisation file

         Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES

Vibrational modes

Table of different vibrational frequencies.

NHmolecule

The number of vibrational modes expected using the 3N-6 rule is 6. Referring to the table of vibrational frequencies, modes 2 and 3 are degenerate with eachother and so are modes 5 and 6. Modes 1,2 and 3 are bending modes and modes 4,5 and 6 are stretching modes. Mode 4 is a highly symmetric mode. The umbrella mode is mode 1. There would be 4 bands in the spectrum due to the degeneracy of modes 2 and 3 and modes 5 and 6. This leaves 4 distinct vibrational frequencies at which ammonia absorbs electromagnetic radiation.

Charge Distributions

A diagram to show how the charge is distributed in an NH₃ molecule.

I would expect there to be a negative charge on the nitrogen atom and positive charges on the hydrogen atoms as nitrogen is the more electronegative of the two.

Reactivity

Nitrogen

Link to the optimisation file

There is only one vibrational mode in this diatmomic molecule with an intensity of 0 because there is no overall dipole shift.

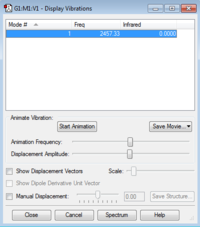
Molecule Name	Nitrogen (N₂)
Calculation Method	RB3LYP
Basis set	6-31G(d,p)
E(RB3LYP)	-109.52359111 a.u
Point Group	D*H
Optimised N-N bond length	1.10550Å
Optimised N-H bond angle	180°

 Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES

N molecule

Hydrogen

Link to the optimisation file

Molecule Name	Hydrogen (H₂)
Calculation Method	RB3LYP
Basis set	6-31G(d,p)
E(RB3LYP)	-1.17853936 a.u
Point Group	D*H
Optimised N-N bond length	0.74279Å
Optimised N-H bond angle	180°

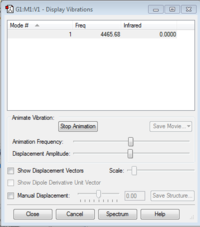
The table shows there is only one vibration mode for the linear molecule and this value in IR is 0.00 as therer is no overall dipole shift because both atoms are the same.

Hmolecule

 Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES

E(NH3)	-56.5577687 a.u
2*E(NH3)	=-113.1155374 a.u
E(N2)	-109.52359111 a.u
E(H2)	-1.17853936 a.u
3*E(H2)	-3.53561808 a.u
ΔE=2E(NH3)-[E(N2)+3E(H2)]	-0.05579070 a.u
ΔE	-146.48kJ/mol

The energy of the reaction is a negative value indicating that the gaseous product, ammonia, is the more stable than the gaseous reactants.

N₂ Molecular Orbitals

Molecular Orbital number 1
Molecular Orbital number 2
Molecular Orbital number 3
Molecular Orbital number 4
Molecular Orbital number 5

ClF₃

Properties

Link to the optimisation file

Molecule Name	Chlorine Trifluoride (ClF₃)
Calculation Method	RB3LYP
Basis set	6-31G(d,p)
E(RB3LYP)	-759.46531682 a.u
Point Group	C2V
Optimised Cl-F bond length(short bond)	1.65143 Å
Optimised Cl-F bond length (long)	1.72863 Å
Optimised F-Cl-F bond angle (small angle)	87.140°
Optimised F-Cl-F bond angle (large angle)	174.281°

Item               Value     Threshold  Converged?
 Maximum Force            0.000050     0.000450     YES
 RMS     Force            0.000028     0.000300     YES
 Maximum Displacement     0.000204     0.001800     YES
 RMS     Displacement     0.000134     0.001200     YES

Vibrational Modes

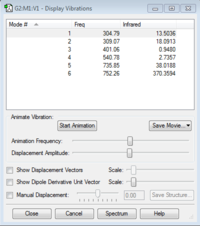
A table showing the frequencies and the IR values of the vibrations in the molecule

The number of vibrational modes expected using the 3N-6 rule is 6. Referring to the table of vibrational frequencies,none of the modes are degenerate and in the IR spectrum I would expect to find 4 bands as two would overlap being very similar in frequency (modes 1 and 2).

Hmolecule

A digram showing the charge distribution in the molecule.

Molecular Orbitals

As the 3 fluorine atoms together have 21 electrons which is a higher number than the chlorine which has only 17, the d orbitals in the chlorine are able to be occupied. This is because when the atomic orbitals combine, the resulting bonding molecular orbitals will be lower in energy than some of the antibonding orbitals.

Molecular Orbital number 1 is the HOMO in the molecule and is a majority antibonding orbital made up from the combination of the 3p_x orbital and the 2p_x orbitals from the fluorines.
Molecular Orbital number 2 is a majority antibonding orbital made from the combination of the p orbitals on the fluorines and the 3p orbital on the chlorine.
Molecular Orbital number 3 is made from the 3d_x²-y² and the 2p orbitals on the fluorines. It is also a majority antibonding orbital.
Molecular Orbital number 4 is made up from the combination of the 3d_xy orbital on the chlorine and the 2p_x from 2 of the fluorines. It is a majority antibonding orbital.
Molecular Orbital number 5 is the combination of the 3d_xz orbital and the 2p orbitals on the fluorines. It is a majority bonding orbital.