Rep:Mod:KK1C

Experiment 1C

Molecular mechanic is a relatively easy way of measuring steric energy of molecules by using classical mechanics. The steric energy consists of many energy terms, and the key features for this method are that each energy term and each atom is treated individually. In this experiment, Avogadro was used to compute and optimize the geometries of various molecules, by using a MMFF94s force field which is an aspect of the constants used in calculations.

Conformational analysis using Molecular Mechanics (Part 1)

The Hydrogenation of Cyclopentadiene Dimer

In the first part of the experiment, the dimerisation products of cyclopentadiene were investigated by optimising the geometries of exo(1) and endo(2) isomers. To discover which of these dimers is the most stable, the energies were calculated using MMFF94(s) force field.

Molecule 1(exo)	Molecule 2(endo)	Molecule 3	Molecule 4
Molecule 1	Molecule 2	Molecule 3	Molecule 4

The energies obtained of molecule 1 and molecule 2 are given below:

Energy terms	Energy of molecule 1(kcal/mol)	Energy of molecule 2(kcal/mol)
Bond stretching	3.54932	3.46838
Angle bending	30.90220	33.18349
Stretch bending	-2.03906	-2.08256
Torsional	-2.90076	-2.95258
Out-of-plane bending	0.01343	0.02177
Van der Waals	12.95993	12.36358
Electrostatic	13.01481	14.18891
Total	55.49987	58.19098

As can be seen from the table, the product 1 (exo) is 2.69111 kcal/mol lower in energy than product 2( endo) and is more stable. This suggests that the exo product is the thermodynamic product and should be the dominat one. But why then it is known that endo product is mainly formed in Diels-Alder reaction between two cylcopentadiene molecules? To understand this, TS geometry has to be considered. When endo product is formed, the two molecules approach each other in such way that they have very favourable secondary orbital interactions, which is not the case for the exo form. Because of the good orbital overlap in TS, the free energy of activation becomes very favourable, TS becomes more stable, and the endo product is formed as a major product. The endo product is the kinetic product of dimerisation. When comparing different energy contributions to the total energy, all the the energy terms are very similar. The biggest difference comes from the angle bending and electrostatic interactions. Higher angle bending energy means that angles at which the atoms are positioned are further apart from the equilibrium angle. This means that endo product has more angular strain. The electrostatics term also favours the exo product. Electrostatic interactions is a Coulombic interaction and is a result of charge interactions between non-bonded atoms(in this case it probably is dipole-dipole interactions).

The hydrogenation of product 2 can give two possible dihydro derivatives-3 and 4. Optimisation was carried out on both of these products and energies were obtained. The table below summarizes the energies of product 3 and product 4:

Energy terms	Energy of product 3(kcal/mol)	Energy of product 4(kcal/mol)
Bond stretching	3.30165	2.81918
Angle bending	31.88363	24.68982
Stretch bending	-2.08979	-1.65580
Torsional	-1.39931	-0.36913
Out-of-plane bending	0.01361	0.00030
Van der Waals	13.64205	10.62720
Electrostatic	5.11963	5.14710
Total	50.47147	41.25866

The energy of the product 4 is lower than that of product 3. The energy of hydrogenation can be calculated for each of the products because the energy of product 2 is also known. So ΔH(hydro, product 2->3)= -7.71951 kcal/mol but ΔH(hydro, product 2->4)= -16.93232 kcal/mol. As both heats of hydrogenations were calculated with respect to the same product 2, the one which is the most exothermic in hydrogenation is also the most thermodynamically stable and that is product 4. So product 4 is the thermodynamic product. Table above shows how the total energy is distributed between the all energy terms. The energy terms can be divided in two parts: one is for bonded interactions(stretching, bending, torsional) and the other for non-bonded interactions( Van der Waals, electrostatic). The biggest difference in energy between two isomers comes from the angle bending and van der Waals energies. Both of these terms are larger for product 3. To understand where the difference comes from, structures have to analysed slightly in slightly more detail. As can be seen in the above model, the first big difference is in the cyclic 5 member ring. The ring of product 3 adopts envelope conformation and is one of the two stable conformers of cyclopentane(the other is half-chair). The 5 member ring of product 4 contains a double bond, and this would suggest some instability compared to product 3. But product 3 contains norbornene derivative and contains double bond, this factor rises energy significantly as a result of increased ring strain. Because of this reason, product 4 is less strained in its cylic structure and is more stable. There is not a very big difference in van der Waals energy and the slightly increased instability for product 3 could come from not perfectly staggered positions of hydrogens in envelope structure.

Atropisomerism in an Intermediate related to the Synthesis of Taxol

The aim for this part of experiment was to investigate two key intermediates in the synthesis of Taxol-products 9 and 10. These intermediates differ with the position of carbonyl group which can point upwards or downwards. As these isomeric conformations are restricted to rotation around bonds they illustrate a special case of isomerism called atropisomerism. This atropisomerism occurs across the carbonyl group and is a result of angular strain.

The molecular models of products 9 and 10 can be viewed in applet buttons:

Using MMFF94s force-field calculations the geometries of both products were optimised. It was found that each product can adopt more than one conformational structure-two chairs and two twist boats.

The other two chair conformations can be viewed here:

The chair conformations were studied in slightly more detail as they may adopt the lowest energy conformation(as for cyclohexane). The energies for chair conformations of product 9 and product 10 are given in table:

Energy	Product 9 chair 1 (kcal/mol)	Product 9 chair 2 (kcal/mol)	Product 10 chair 1 (kcal/mol)	Product 10 chair 2 (kcal/mol)
Total energy	70.64076	83.31127	75.09225	60.61258

Both products can adopt the chair conformations which are significantly lower in energy than the other chair conformation. The energy difference between the highest and lowest energy conformers are 12.67051 kcal/mol and 14.47967 kcal/mol for product 9 and product 10 respectively. The largest cotribution to this difference between conformers comes from torsional and angle strain energies and therefore highest energy molecules posses more torsional and angular strain. This is probably due to strained cyclohexane ring. These molecules show very little reactivity and alkene group in molecule is very 'imune' to hydrogenation. This happens because these molecules are defined as 'hyperstable' alkenes and they are less strained than the parent hydrocarbon.This may seem strange because the geometry adapted by norbornene is not good for double bond, especially if it is located by the bridge. But an example shows that the calculated value of the parent hydrocarbon of product 9 chair conformation 1 is 98.86408 kcal/mol, which is 28.22332 kcal/mol higher than corresponding alkene. The main reason why bridgehead olefins show such stability is because they have less strain energy than its parent hydrocarbon(it has negative OS-olefin strain energy). It is thermodynamically unfavourable to hydrogenate hyperstable alkenes because the parent alkane is not as stable. Molecules 9 and 10 are also medium-sized cyclic structures where bridgehead double bonds are preferred,.

Spectroscopic Simulation using Quantum Mechanics (Part 1)

Spectroscopy of an intermediate related to the synthesis of Taxol

The objective of this part of experiment was to draw a molecule, find the best possible geometry by optimisation and then simulate the ¹H and ¹³C spectra. The results of NMR simulations were also compared to literature values.

NMR had to run for one of the two molecules- 17 or 18. As in the previous exercise with molecules 9 and 10, here each molecule can have two chair conformations. The table which summarizes the findings from the optimization using MMFF94s force-field is shown:

Total energy of chair conformations of products 17 and 18

Energy	Product 17 chair 1 (kcal/mol)	Product 17 chair 2 (kcal/mol)	Product 18 chair 1 (kcal/mol)	Product 18 chair 2 (kcal/mol)
Total energy	104.43221	118.48891	106.79065	101.30527

The obtained total energies show very similar trends to the previous exercise(molecules 9 and 10). It means that additional molecular groups don't significantly alter the trends, but just change the magnitude of energies(more atoms lead to more interactions). The conformational trends also remain. The same chair conformations have the lowest energies.

The lowest energy chair conformations of each molecule are shown below:

Molecule 17	Molecule 18
Molecule 17 chair 1	Molecule 18 chair 2

The NMR simulation was run for the lowest energy conformer of molecule 17 predicting that the literature values are given for this specific conformer. After optimizing the geometry in Avogadro, the input file was sent to HPC with the following parameters: B3LYP/6-31G(d,p), Opt, SCRF=(CPCM,Solvent=chloroform), Freq, NMR, EmpiricalDispersion=GD3. Later the spectra was obtained using TMS as a reference.

¹H and ¹³C NMR spectra of molecule 17

1H NMR spectrum of 17	13C NMR spectrum of 17

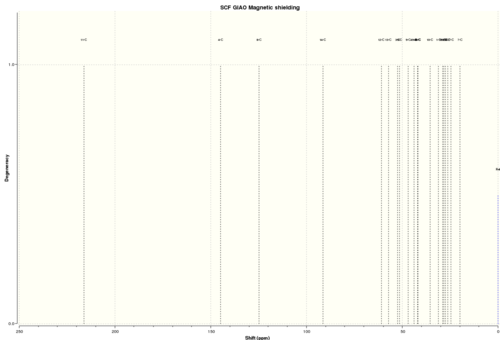The table which summarizes and compares the results ¹H NMR spectrum of lowest energy conformer of product 17 is given,:

Molecule 17 ¹H NMR assigned

Comparison between computed and literature ¹H NMR data of product 17

Nucleus	Protons in NMR spectrum	Literature data (ppm)	Additional information from literature	Computed data (ppm)
A	21	4.84	dd, J=7.2, 4.7 Hz, 1H	5.32
B	52, 53, 50, 51	3.40-3.10	m, 4H	3.18-3.06
C	18	2.99	dd, J=6.8, 5.2 Hz, 1H	3.10
D	22, 23, 24, 25, 33, 34, 35, 36, 39, 40, 41, 42, 43, 44	2.80-1.35	series of m, 14H	2.76-1.57
E	30, 31, 32	1.38	s, 3H	1.46
F	46, 46, 47	1.25	s, 3H	1.21
G	27, 28, 29	1.10	s, 3H	1.13
H	26	1.00-0.80	m, 1H	2.10

There is one major difference between computed ¹H NMR data and literature values and that is methyl group. Computer assigns a value for each of the methyl protons and shows them as a separate peaks, whereas we know that all methyl protons in solution gives one singlet in spectrum as a result of fast rotation of methyl group. For that reason, the average value was calculated of all 3 protons from a methyl group to give a value which can now be compared to literature value. There also was some interesting interpretation of integration(degeneracy) of some protons, for example, 3 of 4 protons from 1,3-dithiolane group were shown to be degenerate with some other proton on the structure. The data were analysed, compared and matched with the structure in the best possible way. Overall, the computed proton chemical shift values match very closely with the literature values. The general trend holds-protons next to double bonds and close to electron withdrawing elements are the most deshielded. The alkene proton is the most deshielded, it couples with two D protons(those between A and C) to give doublet of doublets. Protons(B) from 1,3-dithiolane group have the next highest chemical shift, as predicted. The tertiary proton(C)couples to the same 2 D protons to give doublet of doublets and also has higher shift value than primary and secondary protons. There is series of multiplets for D protons, in total 14 of them. It is probably due to similar chemical shift values and the fact that peaks overlapped. E and F protons have higher shift values because they are spatially closer to oxygen than G protons. The biggest difference in chemical shift for some reason was for proton H. Computed value seems to high even for tertiary proton.

Comparison between computed and literature ¹³C NMR data of product 17

Carbon	11	4	8	14	12	13	3	5	9	49	48	16	10	1	15	19	2	6	17	7
Literature data (ppm)	218.79	144.63	125.33	72.88	56.19	52.52	48.50	46.80	45.76	39.80	38.81	35.85	32.66	28.79	28.29	26.88	25.66	23.86	20.96	18.71
Computed data (ppm)	216.27	144.86	124.71	91.36	60.96	57.08	52.46	51.48	46.92	43.87	41.94	41.88	35.44	31.20	28.94	28.36	27.38	26.33	24.55	19.78

Molecule 17 ¹³C NMR assigned

¹³C NMR chemical shifts are very similar to literature values. On average the shifts differ by 3.21 ppm per carbon. The way this spectrum was analysed is similar to proton NMR spectrum. In some ways it is easier to analyse and match the spectrum because here is no need to calculate the average chemical shift, as it was for ¹H NMR. This worked very well. For the first 3 carbons there is no real doubt whether they have been assigned correctly, because the carbon from carbonyl group should be deshielded the most. Carbons 4 and 8 also should be find downfield and that is the case. The high computed chemical shift for carbon 14 is slightly surprising but as it is attached to two sulphur atoms and has no hydrogens, it could possibly show higher shield values but probably not so significantly as in this case. This could occur due to spin-orbit coupling errors. Carbon atoms attached to heavy elements may have this deviation in chemical shift. A formula that would correct the computed chemical shift for carbon next to two sulphur atoms could be suggested for future comparisons δcorr = δcalc -18.5. Carbons 12, 13, 3, 5 are all tertiary and quaternary carbons and are deshielded more than primary and secondary ones. All the rest are primary and secondary carbons and it is hard to tell whether they have been assigned correctly but literature values are very close to calculated values. Overall the computed values had higher shift values but that can partly be explained by S influence on shifts.

It was also possible to get free energy ΔG (sum of the electronic and thermal fee energies) from the calculations. The table summarizes the findings:

ΔG for different isomers

Structures	Molecule 17 chair 1	Molecule 17 chair 2	Molecule 17 boat	Molecule 18 chair 2
ΔG (Hartrees)	-1651.460768	-1651.440538	-1651.434016	-1651.464194

The most stable conformer should have the most negative ΔG value. If ordering the energies from the most negative to the least one, the folowing series are obtained: molecule 18 chair 2, molecule 17 chair 1, molecule 17 chair 2 and molecule 17 boat. The order of ΔG energies should match the order of total energy calculations above. The ordering is actually the same in both cases. The energy of product 17 boat conformation is 125.91266 kcal/mol. The boat can be viewed here.

¹³C NMR spectra comparison between different conformations of product 17

Difference between literature and computed chemical shift values of compound 17 conformers

Molecule 17 chair 1	Molecule 17 chair 2	Molecule 17 boat

The average difference between literature and computed values for chair 1 conformation was 3.21 ppm per carbon, for chair 2 conformation it was 5.72 ppm but for boat it was 4.59 ppm per carbon. This illustrates that chair 1 conformation is possibly the conformer for which the literature values were given. For all conformers the computed values are mainly larger than literature chemical shift values, except for carbons 11 and 8. From graphs it can be seen that most deshielded carbons actually deviate from literature values the least. The most significant deviation is observed by carbon 14, which is attached to two sulphur atoms. This behaviour could be rationalised by spin-orbit coupling errors.

Analysis of the properties of the synthesised alkene epoxides (Part 2)

This experimental part involved the investigation of the asymmetric epoxidation reaction using the Shi and Jacobsen catalysts to produce different chiral alkene epoxides. The Cambridge Crystal database was used to find the crystal structures of catalytic precursors. Rest of the experiment consisted of chiroptical technique methods-NMR, optical rotation, TS. There also was some investigation of transition state active sites.

The crystal structures of The Shi asymmetric Fructose catalyst and the Jacobsen asymmetric catalyst

The Shi and the Jacobsen asymmetric catalysts are used to epoxidise alkenes. Each of the catalysts has its stable form of precursor. The Cambridge Crystal database was used to find the the precursors of each catalyst.

Structure of molecules 21 and 23

Molecule 21	Molecule 23
Molecule 21	Molecule 23

Both structures were found in Cambridge Crystal database and analysed by Mercury. The names of these molecules were fascinatingly long. Molecule 1 is 1,2:4,5-Di-o-isopropylidene-beta-D-erythro-hexo-2,3-diulo-2,6-pyranose but molecule 23 is Chloro-(N,N'-bis(3,5-di-t-butyl-salicylidene)cyclohexane-1,2-diamine)-manganese. Molecule 21 has two anomeric centres (C 19 and C 22). The bond lengths for C-O bond distances are shown in the model. In both anomeric centres the C-O bond lengths are different. One reason could be that molecule is not symmetric and is strained, so bond lengths are different. But it also could be the specific orbital interaction and an anomeric type interactions. That means that lone pair(good donor) of one oxygen atom interacts with σ* C-O orbital(good acceptor) of the other oxygen in anti-periplanar orientation which in this case is not fully antiperiplanar. Another possibilty would be conjugation of σ C-C(C-C bond coming out of anomeric centres) with σ* C-O orbitals but they also are not perfectly antiperiplanar.σ C-C bond is not as good donor as lone pair because it is lower in energy. Of course, this can also go the reversed way, so obviously for this to be true there must be different strength of interactions coming from each atom. So the C-O bond which is closer to oxygen atom which can better donate the lone pair into empty σ* C-O orbital will be shorter, whereas the other C-O bond will be longer. In both anomeric centres, the two C-O bonds only differ by 0.002 and 0.006 nm which is not huge difference for such a large molecule but could have effect on how, for example, it interacts with molecules in catalysis. It is also worth mentioning that both 5 member rings adopt half-chair structures. Half-chair is one of the lowest energy conformers of cyclopentane, the other is envelope.

In the molecular model of molecule 23, some inter-nuclear distances are shown. At these distances van der Waals dispersion force operates. At very short distances this force can get repulsive and could disfavour the energy of the molecule, but at specific distances it actually becomes attractive and have a good impact of molecule's total energy. The interactions between two atoms depends on the sum of van der Waals radii. This molecule has four very bulky t-butyl groups attached to it. In the middle of molecule, two t-butyl groups approach each other very closely and the closet H-H distances are shown in the model above. The sum of two H's van der Waals radii is about 0.22 nm. One of the H-H interacting distances are actually less than this and is 0.208 nm. When the distance is smaller than the sum of the van der Waals radii, there is a big possibility that this interaction is repulsive, and in this instance it probably is. Rest of the distance are larger than sum of van der Waals radii and are attractive. For the t-butyl groups at sides the distances are much larger than sum of van der Waals radii and could be slightly attractive. The C-C and C-H interactions have larger van der Waals radii but none of the interactions on the molecule are repulsive for these interactions.

Calculated NMR properties of epoxides

Two alkenes were chosen for asymmetric epoxidation reaction-styrene and 1,2-dihydronaphthalene. The resulting products of this reaction are Styrene oxide and 1,2-Epoxy-1,2,3,4-tetrahydronaphthalene. The geometries of molecules were optimised in Avogadro using MMFF94s force field and chemical shift values were computed. Both of these molecules can exist as enantiomers. Styrene oxide exists as (S) and (R) enantiomers but 1,2-Epoxy-1,2,3,4-tetrahydronaphthalene as (1S,2R) and (1R,2S) enantiomers. Important to note here is that 1,2-Epoxy-1,2,3,4-tetrahydronaphthalene has two chiral centres and usually if molecule posseses 2 chiral centres that leads to 4 enantiomers but because this molecule is locked in cis form, only 2 enantiomers exist for this molecule. As NMR should be identical for both enantiomeric forms, calculations were carried out for single enantiomeric form. The computed values were compared to literature values.

Calculated ¹H and ¹³C NMR spectra of Styrene oxide

1H NMR spectrum	13C NMR spectrum

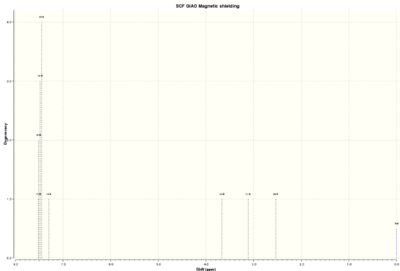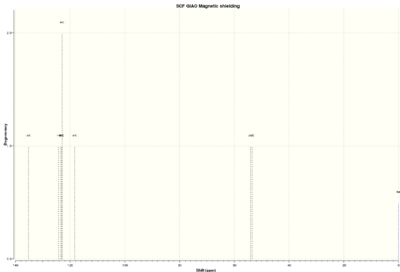The table below shows the calculated and literature values of chemical shifts for Styrene oxide,:

Comparison between computed and literature ¹H NMR data of Styrene oxide

Protons in NMR spectrum	Literature chemical shifts (ppm)	Additional information from literature	Computed chemical shifts (ppm)
13,14,15,16,17	7.42-7.22	m, 5H	7.51-7.30
12	3.85	dd, J=2.6, 4.1 Hz, 1H	3.66
11	3.13	dd, J=4.1, 5.5 Hz, 1H	3.11
10	2.79	dd, J=2.6, 5.5 Hz, 1H	2.53

The computed and literature values are very similar. Five protons from phenyl ring are deshielded the most as a result of ring current and the values differ by about 0.1 ppm. Proton B is the next most deshielded proton which is also reasonable because it is next to electronegative oxygen. It is also not attached to any other proton and could still possibly feel slight effect or ring current. Protons 11 and 10 are the most shielded. For proton 10 the literature and computed values differ by 0.26 ppm which is the biggest difference between all of the protons. Overall, the calculated and literature values are very similar and could possibly suggest that right enantiomeric structures were found.

To get more reliable proof of what has been made, C¹³ NMR spectrum was analysed:

Comparison between computed and literature ¹³C NMR data of Styrene oxide

Carbon	3	7	5	4	6	8	2	1
Literature chemical shifts (ppm)	137.6	128.5	128.5	128.1	125.5	125.5	52.4	51.2
Computed chemical shifts (ppm)	135.14	124.13	123.41	122.96	122.95	118.27	54.05	53.45

The chemical shift values for these carbons differ on average by 3.84 ppm per carbon which is not a big difference and this could mean that right isomer has been optimised. The most deshielded carbon is 3 as it is in aromatic ring and is also close to electronegative oxygen atom. All the aromatic carbons are also the most deshielded because of ring current. Carbon 2 is more deshielded than carbon 1 because it is tertiary carbon whereas carbon 1 is secondary and has more H atoms attached to it( H is less electronegative than C).

Calculated ¹H and ¹³C NMR spectra of 1,2-Epoxy-1,2,3,4-tetrahydronaphthalene

1H NMR spectrum	13C NMR spectrum

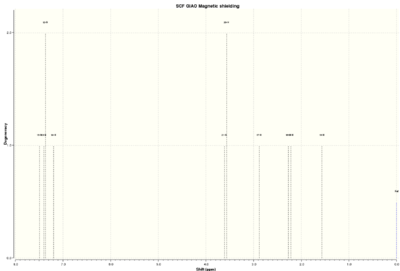The table below shows findings and calculations of 1,2-Epoxy-1,2,3,4-tetrahydronaphthalene ¹H NMR data,:

Comparison between computed and literature ¹H NMR data of 1,2-Epoxy-1,2,3,4-tetrahydronaphthalene

Protons in NMR spectrum	Literature chemical shifts (ppm)	Additional information from literature	Computed chemical shifts (ppm)
15	7.40	dd, J=1.47 and 7.33 Hz, 1H	7.49
12,13	7.28-7.18	m, 2H	7.40-7.37
14	7.09	d, J=7.33, 1H	7.20
21	3.85	d, J=4.39 Hz, 1H	3.61
20	3.73	m, 1H	3.57
17	2.77	ddd, J=6.83, 14.65, and 14,65 Hz, 1H	2.88
18	2.55	dd, J=5.86, 14.65 Hz, 1H	2.22
19	1.77	ddd, J=5.86, 14.65,and 14.65 Hz, 1H	1.56

The literature and calculated values don't differ significantly in ¹H NMR of 1,2-Epoxy-1,2,3,4-tetrahydronaphthalene. The assignment of protons was mainly based of shift values. It is hard to assign aromatic protons without knowing the coupling constants. Coupling constant calculations may have helped to assign them more reliably but they were not done due to time constraints. Otherwise the aromatic proton chemical shifts match with literature values very closely. Aromatic protons have the highest shift values as expected. Protons 21 and 20 differ the most from literature values. This again could be due to spin-orbit coupling errors because they are close to electronegative oxygen atom. As before calculated coupling constant values probably would have helped to assign these protons.

Computed and literature ¹³C NMR data of 1,2-Epoxy-1,2,3,4-tetrahydronaphthalene

Carbon	4	5	10	7	8	9	1	6	3	2
Literature chemical shifts (ppm)	136.5	132.4	129.4	128.3	128.2	126.0	54.9	52.6	24.3	21.7
Computed chemical shifts (ppm)	133.84	130.38	125.56	123.84	123.42	121.44	56.44	54.81	28.04	24.95

As before the calculated C NMR values are very close to literature values. The shift on average differs by 3.306 ppm per carbon. The most deshielded carbons are those in aromatic ring and they were assigned based on shift values. The biggest difference chemical shift values here is for carbon 9. Carbons 6 and 1 are also quite deshielded because they are next to oxygen. Rest of the carbons are more shielded. NMR is useful in checking whether the right structure has been made in reaction or optimised in calculations but it doesn't distinct between enantiomers. Different methods have to be used instead.

Assigning the absolute configuration of the product

This part of experiment involves finding the literature values of optical rotation for styrene oxide and 1,2-Epoxy-1,2,3,4-tetrahydronaphthalene. Computations were also carried out to calculate the optical rotation of molecules using the Cambridge variation on the B3LYP density functional method. These values were then compared for both enantiomeric forms of the molecules. Optical rotation was calculated for both enantiomers of styrene oxide to see whether the magnitudes of rotations match. Enantiomers should have rotations equal in magnitude but with opposite signs.

Calculated and literature values of optical rotations

Calculated and literature values of optical rotations of Styrene oxide

Wavelength (nm)	Calculated values of (R) (o)	Literature values of (R) (o)	Calculated values of (S) (o)	Literature values of (S) (o)
589	-30.33	-21.9	+30.18	+21.1
365	-94.70	n/a	+94.26	n/a

All the literatre values above were obtained in same conditions at 25 ^oC and in CHCl₃. No literature values were found for 365 nm measurements. There are two major differences when comparing values. Firstly, shorter wavelengths give larger optical rotation. One reason could be that shorter wavelength(larger energy) light induces larger rotation because of extra energy that light carries. Secondly, the computed values are about 9 ^o in magnitude larger than literature values. The good thing is that calculated values are about the same in magnitude and have the opposite signs which means that two enantiomers were found. This also means that the optimised geometries are not different conformers because any slight change in structure may lead to significant optical rotation changes. This 9 ^o difference in values could come from the fact that this computational method is only reliable for rotations of about 100 ^o and larger. The results of optical rotation for 365 nm is therefore more reliable than 589. Overall, the results are very good because the calculated values were very similar in magnitude and with an opposite signs.

Calculated and literature values of optical rotations of 1,2-Epoxy-1,2,3,4-tetrahydronaphthalene

Wavelength (nm)	Calculated values of (1S,2R) (o)	Literature values of (1S,2R)(o)	Calculated values of (1R,2S)(o)	Literature values of (1R,2S) (o)
589	-155.91	-131	+155.91	+133
365	-522.52	n/a	+522.52	n/a

The same two trends remain. Literature values are smaller in magnitude than calculated values, and shorter wavelength light gives larger optical rotation. Here the literature values are about 23.9 ^o smaller in magnitude than calculated values but this time the computed results are more reliable.

Using the calculated properties of transition state for the epoxidation reaction of phenylprop-1-ene

The computed free energies of transition states can be used to find the value of enantiomeric excess (ee) of two enantiomers formed in reaction. For this exercise all the computed TS energies were given.

Using Shi catalyst

Eight transition states can be find for the Shi catalytic reaction with phenylprop-1-ene. The table below summarizes the energies, energy differences and K values obtained from the transition state energies:

Transition state energies and K values for Shi epoxidation of phenylprop-1-ene

RR series	Energy of RR series (Hartrees)	SS series	Energy of SS series (Hartrees)	ΔG(RR)-ΔG(SS) (Hartrees)	ΔG(RR)-ΔG(SS) (kJ/mol)	K
TS1 RR	-1343.02297	TS1 SS	-1343.017942	-0.005028	-13.201014	205.52
TS2 RR	-1343.019233	TS2 SS	-1343.015603	-0.003630	-9.530565	46.75
TS3 RR	-1343.029272	TS3 SS	-1343.023766	-0.005506	-14.456003	340.98
TS4 RR	-1343.032443	TS4 SS	-1343.024742	-0.007701	-20.218975	3486.65

Transition states initially were calculated in Hartrees, 1 Hartree=2625.5 kJ/mol. From energy difference ΔG(RR)-ΔG(SS), K value can be found from ΔG=RTlnK. But which K do we use? We want to compare the lowest(the most stable) energy enantiomer TS because those will be the ones which determine the kinetics. So the largest K value is used for further calculations. To find ee, some formulae have to be defined. K=(RR)/(SS) and RR+SS=1 is also true, so we can rearrange the formula to get either RR or SS, where RR and SS are the fractions of enantiomers. When inserting K numerical value the following is obtained: 3486.65=RR/SS; 3486.65=(RR)/(1-RR); and RR=(3486.65)/(3487.65)=0.9997, so SS=0.0003. To find ee the following formula has to be applied: ee=((RR-SS)x 100)/(RR+SS)= 99.94 % RR. So the percentage composition for the Shi catalytic epoxidation is 99.94 % RR and 0.06 % SS. The literature value for this mixture is 90 % RR, which is as predicted by calculations. The lowest energy species are in excess.

Using Jacobsen catalyst

Transition state energies and equilibrium K values for the Jacobsen catalytic reaction with cis-phenylprop-1-ene are given below:

Transition state energies and K values for Jacobsen epoxidation of phenylprop-1-ene

SR series	Energy of SR series (Hartrees)	RS series	Energy of RS series (Hartrees)	ΔG(SR)-ΔG(RS) (Hartrees)	ΔG(SR)-ΔG(RS) (kJ/mol)	K
TS1 SR	-3383.259559	TS1 RS	-3383.25106	-0.008499	-22.3141245	8118.63
TS2 SR	-3383.253442	TS2 RS	-3383.25027	-0.0031720	-8.328086	28.78

Same principles apply for these transitions state energies but instead of RR and SS, now the transition state geometries are SR and RS. Define SR and RS as the fractions of of enantiomers. The K value obtained from the most stable transition state free energy difference is 8118.63. When inserting K numerical value, the following is obtained: 8118.63=SR/RS; 8118.63=(SR)/(1-SR); and SR=(8118.63)/(8119.63)=0.99988, so RS=0.00012. The ee of this reaction is ee=((SR-RS)x 100)/(SR+RS)=99.98 %. So enantiomeric compostions in % is 99.98 % of SR and RS is 0.02 %. The literature value for these enantiomers is 92 % SR, so results agree with the literature value .

Investigating the non-covalent interactions in the active-site of the reaction transition state

TS 4 of (R,R) series for Shi epoxidation

TS 4 of RR series for Shi epoxidation

The energy density calculations were carried out for the phenylprop-1-ene transition state 4 of R,R series. Electron density contour surfaces are very useful for identifying non-covalent interactions in molecule. Non-covalent interactions are hydrogen, electrostatic and van der Waals type interactions and they all can lead to repulsive or attractive interactions. In the molecular model it can be seen how Shi catalyst interacts with phenylprop-1-ene and different interactions have been coloured differently. The bluish red interactions(looks like ring) is a bond formation in transition state and can be ignored. There are mildly repulsive interactions in 6 membered rings and as they mainly consist of carbon atoms which have δ+ charges which results in electrostatic repulsive interactions. There also are some very stong repulsive interactions in 5 membered rings, and this occurs because of highly repulsive δ- charges on oxygens. Attractive interactions were also observed. Hydrogen bonding type interactions have been identified between highly negative oxygens and protons. The largest H bonding is between oxygens 2 and 4(from one of the 5 member rings on catalyst) and protons 37 and 46(from alkenes methyl group). Another example of mildly attractive interactions on this structure is van der Waals interactions. One example is between protons 46 and 37 on alkene. There also are favourable van der Waals interactions between catalyst and substrate, which possibly comes from H 19 and C 42 interactions. Van der Waals interactions can also be negative if the atoms approach too closely each other. Overall the energy of transition state is attractive which favours the formation of product (proton and carbon numbers can be viewed in model above). Important to note that phenyl group is orientated endo with respect to the fructose.

Investigating the Electronic topology(QTAIM) in the active-site of the reaction transition state

TS 4 of R,R series for Shi epoxidation

This method is very similar to the previous one but rather than showing all the interactions, this method gives information about the strongest interactions between atoms so representing covalent bonding. This is shown by bond critical point(BCP) which is a special derivative having curvature.There are 4 different interactions assigned in the image on right. Interaction 1 is a strong interaction between H and C, but this is rather very strong van der Waals interactions that covalent bond. The BCP lies slightly closer to H(purple) atom. BCP 2 is clearly strong covalent bonding between 2 sp ³ hybridized carbon atoms it lies in the middle of bond. Interaction 3 is weak interaction between O and H and is not covalent but has H bonding type interactions. The BCP 3 point lies slightly closer to H atom. The last interaction shown is number 4 and is strongly covalent between C and H. The BCP 4 is very close to H atom in this bond. The general trend for BCP point is that it tends to get closer to element in a bond with the smallest electronegativity.