Rep:Mod:KFC205
Ammonia(NH3)
- NH3 N-H bond length:1.101798 Å
- NH3 N-H-N bond angle:105.741°
Calculation information
- Calculation Method = RB3LYP
- Basis Set = 6-31G(d,p)
- E(RB3LYP) = -56.55776873 a.u.
- RMS Gradient Norm = 0.00000485 a.u.
- Dipole Moment = 1.8466 Debye
- Point Group = C3V
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986297D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Complete optimisation calculations and generated data can be found in this link
NH3 molecule |
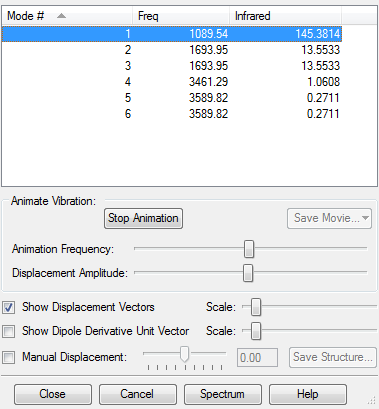
Vibrational Information
- Expected Vibrational Modes=3(4)-6=6
- There are two Bending vibrational modes that are degenerate(number 2 and 3).
There are two Stretching vibrational modes that are degenerate(number 5 and 6. - Numbers 1,2,3 are Bending modes and numbers 4,5,6 are Stretching modes.
- There are two highly symmetric modes, numbers 1 and 4
- The umbrella mode is number 1
- Despite there being 4 different vibrational frequencies predicted,
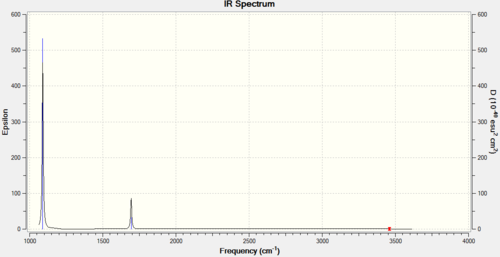
in reality due to the fact that the intensity of vibrations 4-6 is very very low, only 2 bands appear in the spectrum.
This is because the last 3 vibrations(4-6) are very symmetrical and
they don't lead to a large change in the dipole moment, thus are of very low intensity. A picture of the spectrum is included below.
Vibrational mode number 4 is animated below, showing the high symmetry of the motion.
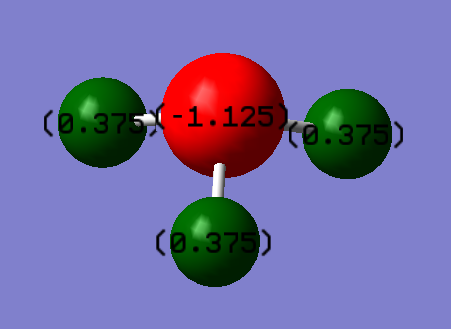
Charge Distribution in Ammonia
As expected the Nitrogen molecule has a partially negative charge build up
because it is one of the most electronegative elements in the periodic table.
Hydrogen, being less electronegative than Nitrogen has a partially positive
charge build up as its electron cloud is polarized by the electronegative Nitrogen.
The Haber-Bosch process
The Haber-Bosch process is used to produce ammonia from its constituent elements in the following equation.
Ammonia is of vital importance in the industrial manufacture of fertilizers and this is done via an iron catalysed Haber-Bosch reaction
N2(g) + 3 H2(g) ⇌ 2 NH3(g)
A closer look at the reactants will yield information for the reaction energies
Nitrogen(N2)
Calculation information
- Calculation Method = RB3LYP
- Basis Set = 6-31G(d,p)
- E(RB3LYP) = -109.52412868 a.u.
- RMS Gradient Norm = 0.00000060 a.u.
- Dipole Moment = 0.0000 Debye
- Point Group = D*H
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.400916D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Vibrational Information
As expected the N2 molecule has only one vibrational mode.
This can be predicted because for non linear molecules:3*2-5=1

Charge Distribution in N2
Due to the homonuclear nature of the bond, there is no ionic component present.
This is because the two nitrogen atoms are identical and hence have the same electronegativity.
As a result there is no net dipole moment or partial charges on the two atoms.
Such bonds are the only ones to be considered 100% covalent
Hydrogen(H2)
Calculation information
- Calculation Method = RB3LYP
- Basis Set = 6-31G(d,p)
- E(RB3LYP) = -1.17853936 a.u.
- RMS Gradient Norm = 0.00000017 a.u.
- Dipole Moment = 0.0000 Debye
- Point Group = D*H
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Vibrational Information
As expected the H2 molecule has only one vibrational mode.
This can be predicted because for non linear molecules:3*2-5=1
Charge Distribution in H2
Due to the homonuclear nature of the bond, there is no ionic component present.
This is because the two hydroden atoms are identical and hence have the same electronegativity.
As a result there is no net dipole moment or partial charges on the two atoms.
Such bonds are the only ones to be considered 100% covalent
Reaction Energy Calculation
- E(NH3)= -56.55776873 a.u.
- 2*E(NH3)= -113.11553746 a.u.
- E(N2)= -109.52412868 a.u.
- E(H2)= -1.17853936 a.u.
- 3*E(H2)= -3.53561808 a.u.
- ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.0557907 a.u.
The enthalpy change is -146.48 kJ/mol and thus it can be deduced that the ammonia product is more stable.
This is because this is an exothermic reaction and therefore the product, NH3 is lower in energy than the reactants H2 and N2
Disulfur(S2)
- S2 bond length:1.92943 Å
This value was confirmed against literature values.
The experimentally determined value (from infrared spectroscopy) is between 189 - 193 pm or 1.89-1.93 Å,
which is in agreement with the calculated value and thus the simulation can be considered accurate [1][2]. - S2 bond angle:N/A (linear molecule)
Calculation information
- Calculation Method = RB3LYP
- Basis Set = 6-31G(d,p)
- E(RB3LYP) = -796.32599779 a.u.
- RMS Gradient Norm = 0.00000372 a.u.
- Dipole Moment = 0.0000 Debye
- Point Group = D*H
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.000011 0.001800 YES
RMS Displacement 0.000016 0.001200 YES
Predicted change in Energy=-7.077697D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.9294 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Complete optimisation calculations and generated data can be found in this link
S2 molecule |
Vibrational Information
As expected the Disulfur molecule has only one vibrational mode.
This can be predicted because for non linear molecules:3*2-5=1.
An animation of the vibration of Disulpur is included below.
It can be seen that the sulfur atoms are vibrating about their equilibrium separation.Using the Lennard-Jones potential,
the vibration can be modeled by Simple Harmonic Motion around that separation.
Because of the symmetry of the vibration, it will not lead to a change in the dipole moment of the molecule
and thus will not absorb in the IR Hence normal Infrared spectra will not display peaks for such vibrations.
Raman spectroscopy however will be able to detect this vibration because the selection rules are different.
Charge Distribution in Disulfur
Due to the homonuclear nature of the bond, there is no ionic component present.
This is because the two sulfur atoms are identical and hence have the same electronegativity.
As a result there is no net dipole moment or partial charges on the two atoms.
Such bonds are the only ones to be considered 100% covalent
Reaction Energy for H2S Formation
S2(g) + 2 H2(g) ⇌ 2 H2S(g)
The following reaction energy data for H2S have been calculated using GaussView 5.0.9
- E(H2S)= -399.39162414 a.u.
- 2*EH2S)= -798.78324828 a.u.
- E(H2)= -1.17853936 a.u.
- 2*E(H2)= -2.35707872 a.u.
- E(S2)= -796.32599779 a.u.
- ΔE=2*E(H2S)-[2*E(H2)+E(S2)]= -0.10017177 a.u.
The enthalpy change is -263.000982135 kJ/mol and thus it can be deduced that H2S is more stable.
This is because this is an exothermic reaction and therefore the product is lower in energy than the reactants H2 and S2.
However because of the entropic nature of the reaction, the forward reaction displayed above doesn't actually happen.
Despite it being exothermic, because of the large decrease in entropy due to moving from 3 moles of gas to 2 moles of gas, the formation of H2S is only thermodynamically feasible at very low temperatures and thus is not the preferred method of producing H2S.
Molecular Orbitals Visualization
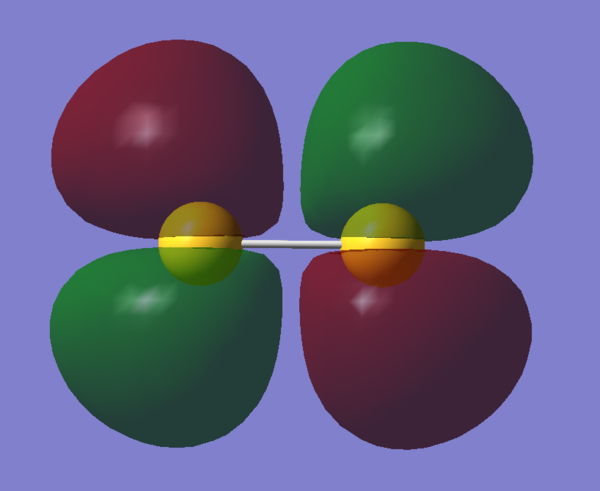

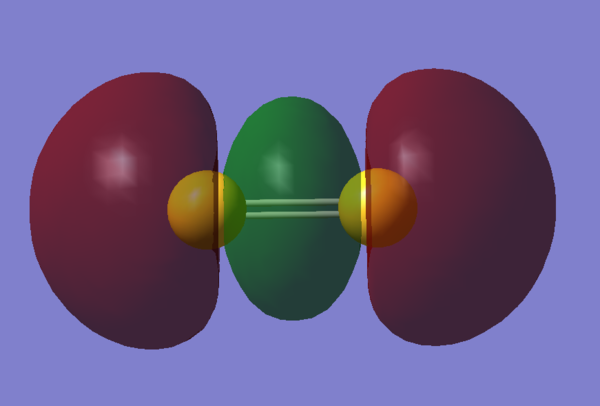
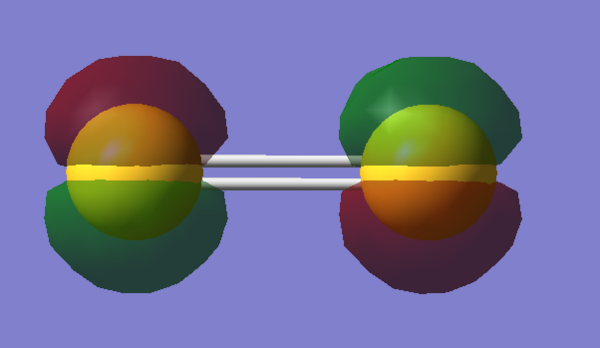

References
[1] Tardif, Sylvie L.; Rys, Andrzej Z.; Abrams, Charles B.; Abu-Yousef, Imad A.; Lesté-Lasserre, Pierre B. F.; Schultz, Erwin K. V.; Harpp, David N. (1997). "Recent chemistry of the chalcogen diatomics". Tetrahedron. 53 (36): 12225–12236. doi:10.1016/S0040-4020(97)00555-3
[2] Spencer, J. R. (2000). "Discovery of Gaseous S2 in Io's Pele Plume". Science. 288 (5469): 1208–1210. Bibcode:2000Sci...288.1208S. doi:10.1126/science.288.5469.1208. ISSN 0036-8075.