Rep:Mod:Jw1707c
Introduction
This module will focus on using theoretical and computational methods to optimise and calculate properties of the transition state in reactions. The methods used here differ from those in the previous units as we are no longer seeking the minimal energy to find the optimised conformation. Two different methods were used as described below:
Cope rearrangement tutorial
Optimisation of starting product
Initially the starting product of a simple cope reaction was optimised:
The 1,5 hexadiene was built in the Gaussview programme and the dihedral angle set to give an anti configuration. This was optimised using the relatively low basis set; HF/3-21G.
Even this relatively simple molecule can have many different configurations as each C-C bond can rotate to give a different relative conformation. These different configurations will obviously have different symmetries and different energies based on several factors
The first optimisation gave the anti2 conformation, the molecule was rearranged manually by adjusting dihedral angles and several different conformers were optimised the key ones are summarised in the following table:
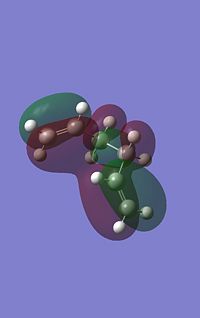
One would initially expect the lowest energy conformation to be an anti conformation, such that all the carbons are anti periplanar to eachother minimising steric repulsions yet the Gauche3 is the lowest energy conformation (although marginally) The reason for this is that the energy is not just dependent on steric factors. There is also hyperconjaction effects and Molecular Orbital overlap effects, as can be seen in the following image. There is a stabilising overlap effect between the pi clouds over the two alkene bonds, this isn't present in the anti configurations as the alkene groups are seperated away from eachother by the antiperiplanar bonds.
Further optimisation of anti conformation
The Anti2 conformation was used as the starting product in our theoretical cope rearrangement. So it was further optimised with a higher B3LYp-631-G(d) basis set. The resulting structure had an energy of -234.61170277a.u. which is a significant drop in energy compared to the previous optimisation. The actual change in geometry was marginal with the only noticeable difference being a change in bond angle between the H-C-H on the central carbons from 107.7° to 106.7°
A vibrational calculation was made at the same basis set to the frequency values, this confirmed that the geometry was at a minimum by providing all positive values as well as giving us frequency information.
The following thermo-chemistry results were produced:
Sum of electronic and zero-point Energies = -234.469212 Sum of electronic and thermal Energies = -234.461856 Sum of electronic and thermal Enthalpies = -234.460912 Sum of electronic and thermal Free Energies = -234.500821
Of particular importance is the first and second values which tell us the potential energy at 0°K and 298.15°k respectively.
Chair and Boat Conformation
Now that the starting product has been optimised, the next stage is to optimise the transition structure. There are two possible transition structures known in the literature, these being the boat and the chair conformation.
Chair C2h transition state
TS berny method
Initially an allyl fragment was drawn and optimised at the HF 3-21G level. Two of these fragments were constructed and placed one on top of the other facing apart in a rough chair conformation. A Gaussian calculation was set up to to compute the transition state optimisation and frequency. The job ran well and the output file showed a single negative frequency at -818cm−1 which corresponded to the expected cope rearrangement as can be seen below:
Vibration |
Frozen Coordinate Method
The alternative method for finding the transition state structure is to freeze the reaction coordinate except for the bond being broken and formed. The rest of the molecule is optimised to a minimum and then the bonds are optimised for the transition state. This method has the advantage that the more complicated transition state calculation is limited to the bonds being broken and formed, so it can be a time saving technique.
The resulting transition state came out with an almost identical transition state structure as can be seen,
Pentahelicene |
The bond length of the bond forming/breaking was 2.02076A as opposed to 2.02054A which is pretty much the same within the level of accuracy of the calculation and the geometry in terms of bond angles was virtually indistinguishable. This proves the idea that certainly in terms of this simple reaction these two methods to calculate the transition state are equally accurate.
Boat C2v transition state
To find the transition state structure a different method was used, the QST2 method works by inputing the starting and final product geometries and the computer will interpolate between the two to find the transition state structure. As with the two previous methods the computation will fail if you dont provide structures close to the optimum one. When the anti2 structure geometry was used the calculation was unsuccessful. Using a more gauche starting structure successfully gave the following boat transition structure, which was confirmed with a vibration calculation which gave a negative frequency corresponding to the cope rearrangement.
Vibration |
Connecting the transition state geometry to the starting product geometry
From looking at the transition state it is difficult to tell what the geometry of the reactant and product is. However using the Intrinsic Reaction Coordinate method allows us to follow the potential energy surface to the local minima and hence the optimised geometry. The calculation from the chair transition state was given 50 steps but only 24 steps were used as can be seen in the following plot:
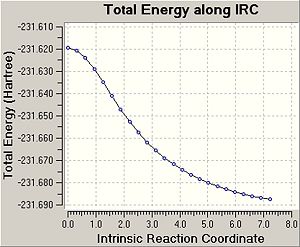
The geometry however still wasn't at a fully minimal geometry yet so the final product was further optimised using a regular optimisation calculation.
The result of this calculation was to give a structure with the same symmetry and energy as the Gauche2 structure. As seen here:
Activation Energies
The activation energy is the difference in the energy between the starting product and the transition state. However the level basis set used so far isn't very accurate for the energies, so the structures were first optimised to the higher level basis set B3LYP 6-31G(d).
Pentahelicene |
This didn't change the geometries visibly as can be seen, but gave significantly lower energies. The energies obviously depend on the temperature. The difference in the Sum of electronic and thermal energies was to calculate the activation energy at room temperature and the Sum of electronic and zero-point energies was used to for the reaction at 0°K. To compare the activation energies with those found in the literature the energies were converted into Kcal/mol.
e.g for the chair transition state:
At Room Temperature: -234.409009 - (-234.461856) = 0.052847 x 627.509 =33.16kcal/mol At 0°K: -234.414930 - (-234.469212) = 0.054282 x 627.509 =34.06kcal/mol
These results make sense as one would expect more energy to be required to overcome the activation barrier at a lower temperature.
The last value is very close to the literature value of 33.5 ± 0.5kcal/mol at 0°K (presumably from extrapolation as the reaction obviously can't be done at 0°K ) implying that the computational model is fairly accurate and presumably at a higher basis set it would be even more so.
Although for the boat structure the activation energy was a bit further off (41.96 kcal/mol vs 44.7 ± 2.0 kcal/mol) experimentally at 0°K.
These results imply that the cope reaction will kinetically go via the chair structure.
Diels Alder
In this part of the lab the same calculations as used for the cope rearrangement were used to find the transition state for a diels alder reaction, initially the most simple diels-alder reaction was computed and then a more complicated reaction with maleic anhydride was calculated and the calculation was used to explain the stereospecific nature of the reaction. For this section the transition states were first optimised using the semi empirical AM1 molecular orbital basis set which was fairly fast for these bigger molecules but generally a low basis set. Once the transition states had been optimised they were then re-optimised at the higher B3LYP 6-31G* basis set which gives more accurate results.
Cis Butadiene and Ethene
Optimisation of Fragments
Initially the starting proeducts were drawn on gaussview and optimised The cis butadiene starting product was constructed and the HOMO and LUMO orbitals visualised.

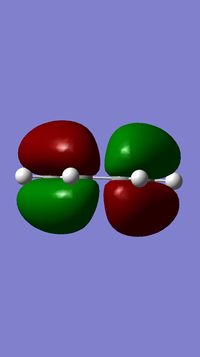
With respect to a plane of symmetry dissecting the molecule vertically, the HOMO can be seen to be antisymmetric whilst the LUMO is symmetric.
Whilst for the ethene molecule, the opposite is the case. This is very significant as a reaction will only occur between two molecular orbitals of the same symmetry.
Transition State Optimisation
Putting the two optimised structures in the same window and optimising the approximate angles and bond lengths manually, before doing a Berny Transition state structure optimisation, yielded eventually a transition state structure. Seen here:
Pentahelicene |
The molecular orbitals of this transition state structure was visualised, of particular importance is the HOMO and LUMO orbitals seen in the images on the side,
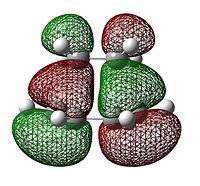
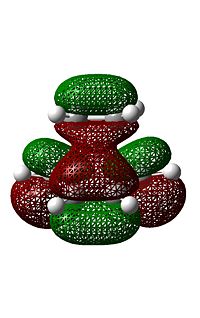
As can be seen, with respect to the same vertical plane, the transition state HOMO is antisymmetric while the LUMO is symmteric. A closer look at the transition state HOMO shows that it is essentially made up of an overlap between the butadiene HOMO and the ethene LUMO, which both had antisymmetric symmetry as stated above. In addition there is a large amount of electron density between the ethene fragment and the butadiene fragment indicating where the bond is forming.
The calculated bond length of the C-C bond being formed in the transition state structure is 2.119Å, this compares to typical σ C-C bond lengths of 1.53Å or 1.46Å for sp3 and sp2 C-C bonds respectively (from the CRC handbook of chemistry and Physics 90th Edition)showing that the bond clearly isn't a proper covalent bond and yet the van-der-waals radius of a carbon atom is 1.70Å so the bond length of 2.12Å is clearly a lot less than the 3.40Å we would expect of there was no bonding whatsoever, instead we have some intermediate stage if bonding which is what one would expect at the transition state.
A look at the vibrational frequecies, shows one negative/ imaginary frequency which confirms that this is indeed a maximum on the potential energy surface. A look at this vibration also tells us a bit about the reaction:
Vibration |
The reaction can clearly be seen to be synchronous, i.e. both bonds are being formed at once. This clearly demonstrates that the diels alder reaction is concerted and not done in steps. A look at the lowest couple of positive frequencies show an interaction between the butadiene and the ethene but asynchronously as seen here:
Cyclohexa-1,3-diene and maleic anhydride diels alder reaction

The previous reaction was between to symmetric molecules, we will now calculate the transition states for a diels alder reaction which can take one of two stereoisomers, a comparison of the properties of the two stereoisomers will give us more insight into the nature of the reaction and allow us to predict which stereoisomer will be formed in a kinetic reaction.
The transition structures were computed as above using the Berny Force field Transition State calculation, giving the following endo and exo products respectively:
Pentahelicene |
Pentahelicene |
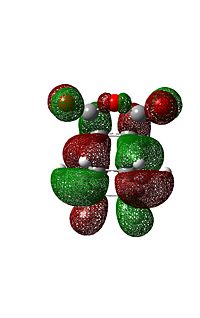

The difference between the endo and exo forms is that in the endo case the three oxygen atoms of the maleic anhydride are tucked in under the alkene groups in the cyclodiene whereas in the exo case they are point out. It is clearly the electrostatic and steric interactions between the alkenes and oxygens which will determine which is more stable. A quick look at the output file gives the endo energy as -612.68339704 hartree and that of the exo as -612.67931095. Which has an energy difference of 10.73 kJ/mol. Showing the endo to be lower in energy, since this is a kinetically controlled reaction, this means that the endo should be the major product which it is experimentally.
In the endo isomer the bond length of the bonds being formed was calculated as 2.27Å whereas this bond length was 2.29Å in the exo structure.
The distance between the carbon on the O=C-O-C=O fragment and the C on the opposite CH on the other fragment was 2.991Å for the endo and 3.03Å for the equivalent C to CH2 in the exo. This seems to imply that the maleic anhydride fragment is being pulled in, in the endo isomer but being pushed away in the exo isomer.
The reason for these differences in bond length can be explained by a closer look at HOMO of each isomer and the phenomenon of secondary orbital overlap[1] . In the endo isomer there is no node between the orbitals on the central oxygen and and the orbitals on the alkenes of the other fragment, the molecule tries to maximise this overlap by bringing the two fragments nearer but on the other hand the steric repulsion between the two fragments is increased by bringing them nearer so an equilibrium value is found, however the exo fragment has a node between the oxygen orbitals and opposing fragment and therefore the molecule doesn't want to pull the fragments any closer and hence the difference in the carbon carbon distances.
References
- ↑ Marye Anne Fox, Raul Cardona, Nicoline J. Kiwiet J. Org. Chem., 1987, 52 (8), p 1469DOI:10.1021/jo00384a016