Rep:Mod:JuliansWiki
Ammonia (NH3)
Optimization
Calculation method: B3LYP
Basis Set: 6-31G(d,p)
Final energy E(RB3LYP): -56.557769 Hartree
Point Group: C3v
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986285D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Optimized N-H bond length: 1.02Å
Optimized H-N-H bond angle: 105.7°
ammonia |
The optimisation file is linked to here
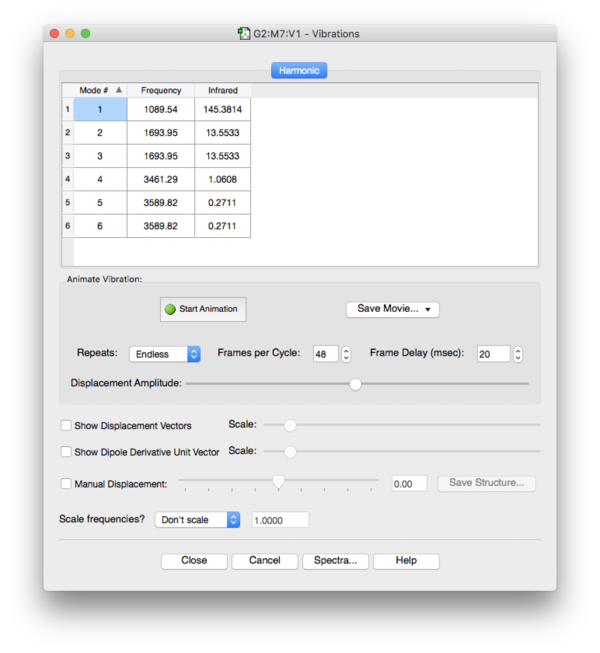
Frequency Analysis
No imaginary frequencies found during frequency analysis, the optimized structure is a true minimum.
Expected number of modes by 3N-6: 3*4-6=12-6=6 which equals the calculated number of vibrations.
Degenerate vibrations have the same energy/frequency: modes 2 & 3 with 1694cm-1 and modes 5 & 6 with 3590cm-1.
Modes 1-3 are bending vibrations and 4-6 are stretching vibrations.
The stretching vibration at 3461cm-1 is the most symmetric vibration.
Mode 1 at 1090cm-1 is the so-called umbrella mode.
6 IR-active vibrations have been identified and 4 of them are pairwise degenerate which results in a number of 4 bands to be expected in a real gas phase IR-spectrum of ammonia. The real number of bands will probably reduce to 3 because the high energy modes at 3461cm-1 and 3590cm-1 are too close to be resolved in a real IR-spectrum.
Charge Analysis
Calculated NBO charge on N: -1.125
Calculated NBO charge on H: 0.375
It was expected to have a negative charge placed on the nitrogen atom because the electron negativity of N (3.07) is higher than that of H (2.20).
Structure and Reactivity
Dinitrogen (N2)
Optimization
Calculation method: B3LYP
Basis Set: 6-31G(d,p)
Final energy E(RB3LYP): -109.524129 Hartree
Point Group: D∞h
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.400986D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
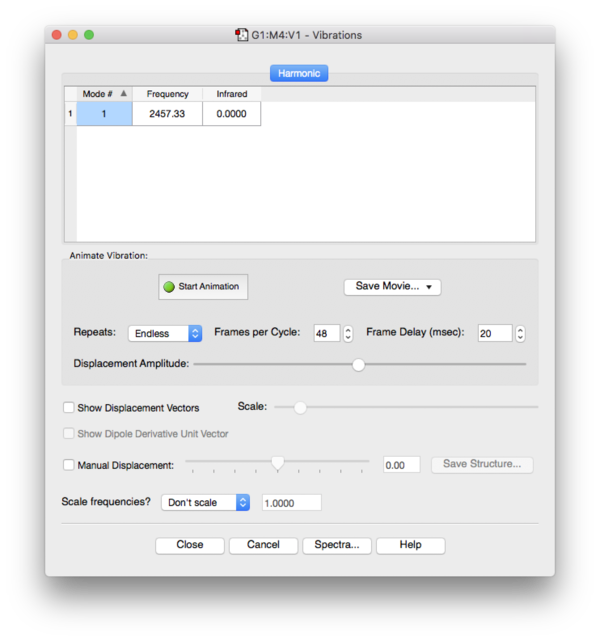
Optimized N-N bond length: 1.11Å
dinitrogen |
The optimisation file is linked to here
Frequency Analysis
No imaginary frequencies found during frequency analysis, the optimized structure is a true minimum.
Dihydrogen (H2)
Optimization
Calculation method: B3LYP
Basis Set: 6-31G(d,p)
Final energy E(RB3LYP): -1.178539 Hartree
Point Group: D∞h
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
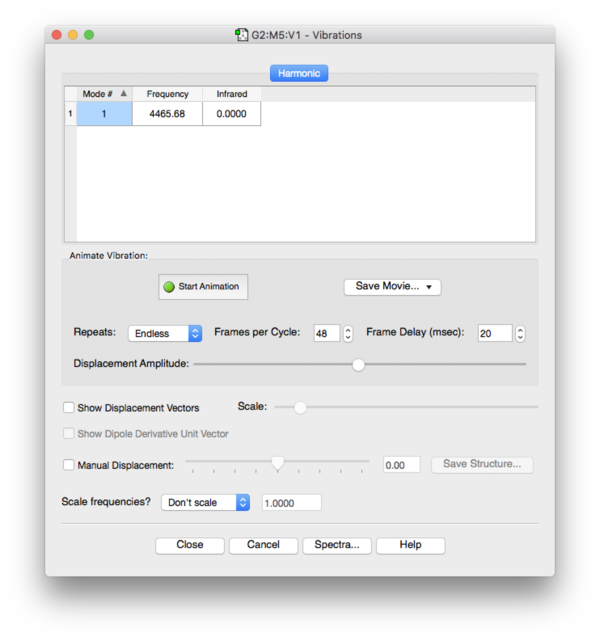
Optimized H-H bond length: 0.74Å
An example for a monometallic dihydrogen complex is (σ2-dihydrogen)-tricarbonyl-bis(tri-iso-propylphosphine)-tungsten CEJDEA. The H-H bond distance in this complex determined by X-ray and neutron diffraction is reported as 0.75(16). The calculated bond distance for dihydrogen in the gas phase is subtly truncated indicating that in the complex electron density between the two H atoms is lowered to allow binding to the tungsten centre. This results in a weakened H-H bond with a longer H-H distance.
dihydrogen |
The optimisation file is linked to here
Frequency Analysis
No imaginary frequencies found during frequency analysis, the optimized structure is a true minimum.
Haber-Bosch cycle
E(NH3)=-56.557769 Hartree
2*E(NH3)=-56.557769 Hartree*2=-113.115538 Hartree
E(N2)=-109.524129 Hartree
E(H2)=-1.178539 Hartree
3*E(H2)=-1.178539 Hartree*3=3.535617 Hartree
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]=(-113.115538-[-109.524129-3.535617]) Hartee=-0.055792 Hartree
-0.055792 Hartree equals -146.5kJ/mol, so in the gas phase ammonia is more stable than the equivalent amounts of dinitrogen and dihydrogen.
Own small molecule - Hydroxide ion (OH-)
Optimization
Calculation method: B3LYP
Basis Set: 6-31G(d,p)
Final energy E(RB3LYP): -75.726292 Hartree
Point Group: D∞h
Item Value Threshold Converged?
Maximum Force 0.000003 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.000004 0.001800 YES
RMS Displacement 0.000006 0.001200 YES
Predicted change in Energy=-1.346204D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.9834 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
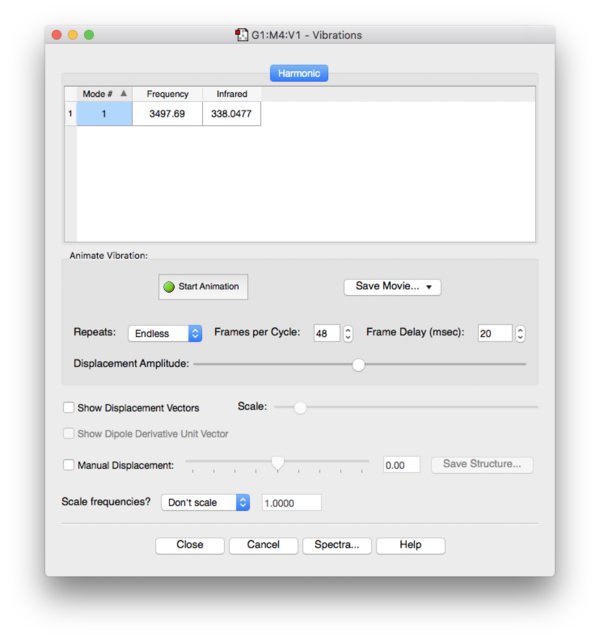
Optimized O-H bond length: 0.98Å
hydroxy ion |
The optimisation file is linked to here
Frequency Analysis
No imaginary frequencies found during frequency analysis, the optimized structure is a true minimum.
Charge Analysis
Calculated NBO charge on O: -1.285
Calculated NBO charge on H: 0.285
It was expected to have negative charge localized on the oxygen atom because the electron negativity of O (3.50) is higher than that of H (2.20).
Molecular Orbitals
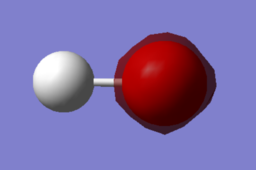 |
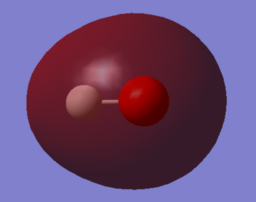 |
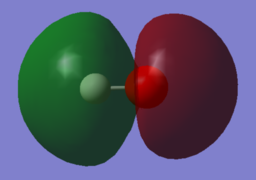
|
| MO 1 | MO 2 | MO 3 |
 |
 |
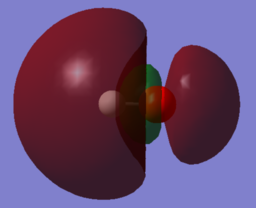
|
| MO 4 | MO 5 | MO 6 |
MO 1 to MO 5 are occupied by an electron pair each. MO 6 is unoccupied.
MO 1 and MO 2 are the two MOs lowest in energy.
MO 1 is simply the 1s orbital of O which lies too low in energy to participate in bonding with the H atom. Therefore, MO 1 is a non-bonding MO.
MO 2 is the bonding combination of the 1s orbital of H and the 2s orbital of O.
The four MOs MO 3 - MO 6 energetically lie in the HOMO/LUMO region, including the HOMO MO4 & MO 5 and the LUMO MO 6. The energy order of the MOs is the following: MO 3 < MO 4 = MO 5 < MO 6.
MO 3 is the binding combination of the 1s orbital of H and the 2pz orbital of O.
MO 4 and MO 5 are the 2px and 2py orbitals of O and are degenerate. Due to their symmetry no interactions with the 1s orbital of H are possible, so both of them are non-bonding and resemble the HOMO.
MO 6 is the binding combination of the 1s orbital of H and the 2pz orbital of O. MO 6 is unoccupied and resembles the LUMO of the hydroxide ion.